高速曳引电梯提升钢丝绳水平方向振动的分析与研究
黄龙涛 王海平 屈 涛 刘继征 刘 海
陕西省特种设备检验检测研究院 西安 710048
0 引言
随着高层建筑快速的发展,高速曳引电梯被广泛应用。在动力学性能方面,国内高速曳引电梯与国外还存在较大差距,尤其是提升钢丝绳振动方面最为突出,是电梯减振技术的核心问题。在电梯运行过程中存在曳引机偏心旋转、导轨不平度等问题,提升钢丝绳以水平方向振动为主,而侧向振动不明显,故对提升钢丝绳水平方向振动的研究十分有意义。
1 高速电梯提升钢丝绳水平方向振动模型建立
高速电梯在运转过程中,提升钢丝绳长度会随着时间的变化而变化,也导致曳引钢丝绳阻尼与刚度产生变化。集中参数离散模型是把提升钢丝绳简化成弹簧—阻尼系统[1],忽略提升钢丝绳的时变性与连续性,故本文采用分布参数连续模型。提升钢丝绳上、下端分别和曳引轮、轿厢相连,补偿绳上、下端分别和轿厢、张紧轮相连。分析提升钢丝绳振动情况下张紧轮的预紧力和虑补偿绳的质量很重要[2],同样导轨对提升钢丝绳的影响也相当重要。为了突出张紧轮的预紧力和虑补偿绳的质量与导轨的影响,建立了高速曳引电梯提升钢丝绳水平方向振动模型,如图1所示。
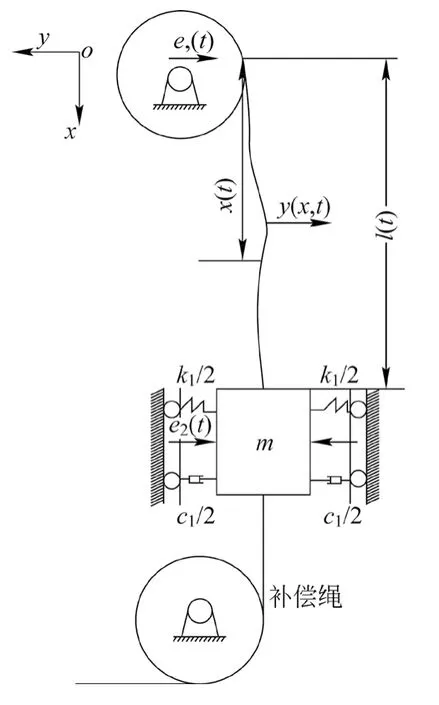
图1 高速曳引电梯提升钢丝绳水平方向振动模型
1.1 水平方向振动控制方程建立
本文中模型建立和求解基于4个假设[3]:1)不考虑井道内部摩擦力、气流的影响;2)忽略补偿绳振动的影响;3)忽略提升钢丝绳侧向振动、扭转等因素的影响,同时水平方向振动产生的弹性变形量要比整条弦线长度小;4)提升钢丝绳弹性模量E、横截面积A、线密度ρ保持不变。
将提升钢丝绳简化为轴向运动的变长度弦线[4],将轿厢简化成质量为m的刚性重物,连接在变长度弦线的下端,纵向自由;将导轨简化成阻尼系数为c1的阻尼器、刚度为k1的弹簧;外界激励为e1表示电动机偏心旋转的影响;水平激励e2为导轨的不平度的影响。弹性模量为E、横截面积为A、线密度为ρ、补偿绳长度为h-L(t),h为提升高度,补偿绳线密度为ρ1。选取提升钢丝绳与曳引轮的切点为原点,垂直向下为x轴的正方向,i为x轴方向的单位矢量,水平向左为y轴的正方向,j为y轴方向的单位矢量。利用连续介质有限形变的理论可得到,提升钢丝绳x处位移向量R为

对式(1)中时间t求导得提升钢丝绳x处的速度向量为

对式(2)进一步简化为
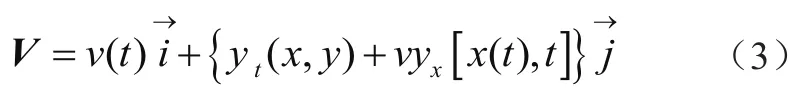
式中:yx[x(t),t]为y[x(t),t]对x的偏导,yt[x(t),t]为y[x(t),t]对t偏导,分别用y、yx、yt表示y[x(t),t]、yx[x(t),t]、yt[x(t),t]。
同理可得提升重物位移与速度的向量分别表示为

由式(3)、式(5)可得,系统动能为
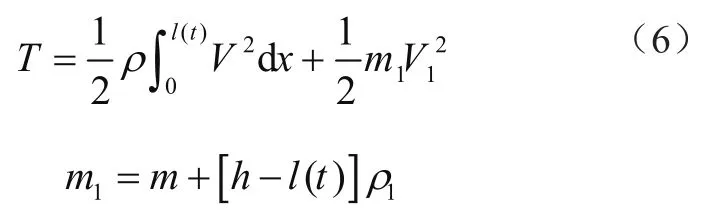
系统势能则表示为
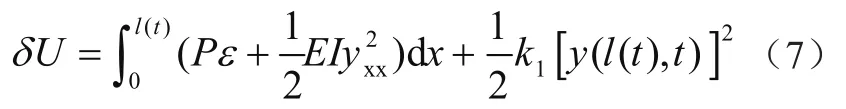
式中:ε为曳引钢丝绳的应变。

式(9)忽略高阶项可得

将式(10)代入到式(8)中可得

将式(11)代入式(7)中可以得到势能为

式中:P为在时间t提升钢丝绳在x处受到的张紧力。
提升钢丝绳受到自重与轿厢重力以及补偿绳的重力、预紧力的作用,故张紧力P表示为
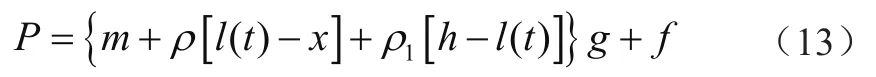
系统阻尼力的虚功表示为
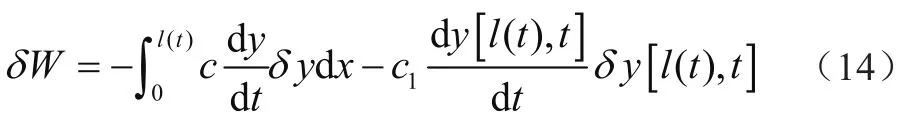
式中:c为提升钢丝绳的分布阻尼。
根据Hamilton原理[3]

进行积分与变分运算时,因提升钢丝绳的长度是时变的,故式(15)中对t积分上限同样是时变的,使用分部积分法与参变量积分求导法
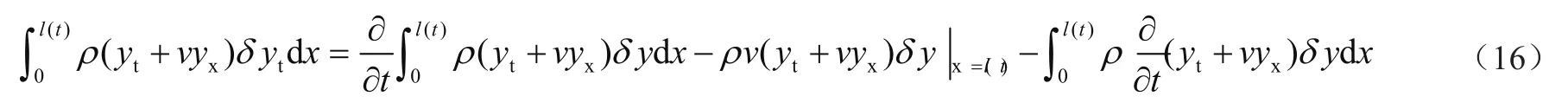
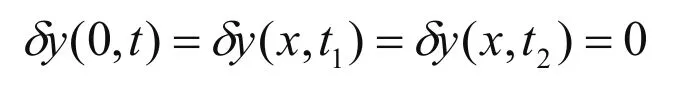
将式(15)进行一系列的变换运算后,可以得出高速曳引电梯提升钢丝绳的水平方向的振动控制方程
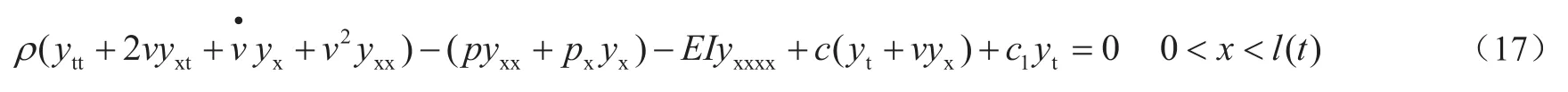
相应时间与几何边界条件分别表示为
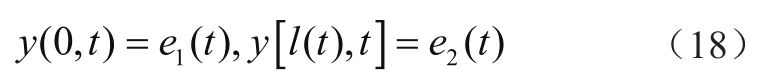
式(18)为非齐次边界条件,齐次边界条件由非齐次边界条件转化,此时引入齐次边界条件函数y1(x,t),水平方向位移y(x,t)表示为

式中:y1(x,t)为满足齐次边界条件区域,y2(x,t)为不满足齐次边界条件区域。
将式(19)代入式(17)可以得到在激励作用条件下高速曳引电梯提升钢丝绳的水平方向振动控制方程为
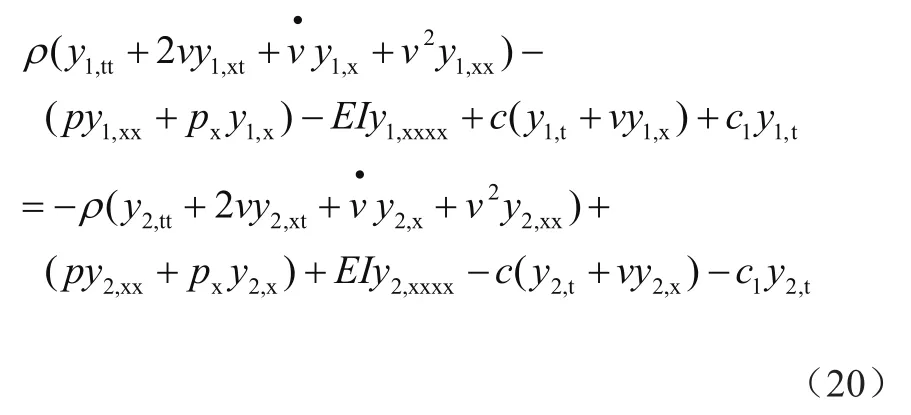
1.2 基于Galerkin法的提升钢丝绳水平方向振动偏微分方程离散
Galerkin法[3]原理:叠加所选取的有限多项式函数,使结果满足求解范围,并且让边界加权积分满足原方程式,可以得到求解简单、满足边界条件的线性方程式。本文利用Galerkin法对高速曳引电梯提升钢丝绳水平方向振动偏微分方程进行离散化处理。
离散化处理前先定义一个无量纲参数ξ,归一化处理原变量,即ξ=x/l(t),将x时变域转成ξ固定域[0,1],设方程式(20)解为
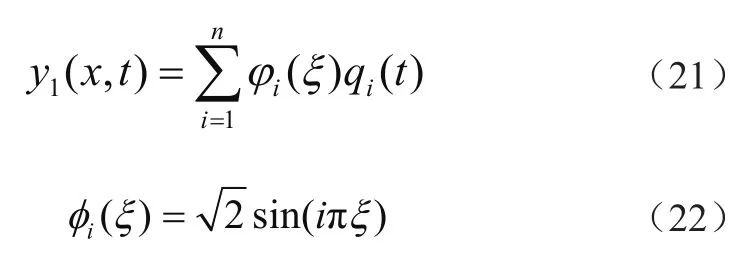
式中:qi(t)为广义坐标;i=(1,2,…n),n为模数;φi(ξ)为形函数。
将式(22)代入到式(21),并求导可得
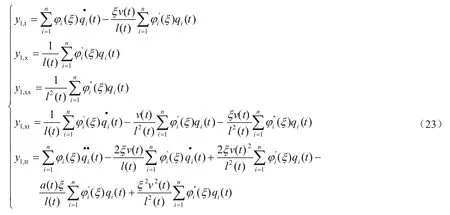
将式(23)代入到式(20)中,且等式两边乘以φj(ξ),然后将ξ在[0,1]内进行积分,可以得到将高速曳引电梯提升钢丝绳水平方向振动无限维度偏微分方程转化成有限维度常微分方程,即
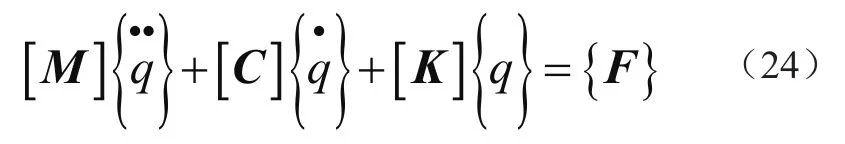
其中:q=[q1(t),q2(t),……,qn(t)]T表示广义坐标向量;矩阵M、C、K、F中各元素值分别表示为

式中:δij为delta函数,若i≠j,则δij=0,若i=j,则δij=1。
式(24)求解后,可计算广义坐标向量q代入到式(19)中,得到了提升钢丝绳水平方向振动实时值。
2 提升曳引绳振动模型参数影响分析
本文以高速曳引电梯工作原理为基础,结合某工况下最大速度vmax=5 m/s、最大加速度amax=1 m/s2、最大加加速度Jmax=0.5 m/s3、最大提升高度lmax=150 m、E=8×1010N/m2、ρ1=0.343 kg/m、e1=0.01sin(3.14t)、e2=0.005sin(6.28t)电梯参数为输入,使用Matlab的Newark-β法仿真分析高速电梯单根提升钢丝绳的提升质量m、分布阻尼c、线密度ρ、预紧力f对其提升钢丝绳水平方向振动的影响。
结合4个参数设计了4个案例,每案例都有3种工况。案例1取m分别为400 kg、500 kg、550 kg;案例2取c分别为0.25、0.5、1;案例3选用碳素钢、结构为8×19类别的提升钢丝绳,提升钢丝绳公称直径分别为10 mm、12 mm、16 mm,取ρ分别为 0.512 kg/m、0.7 kg/m、0.87 kg/m;案例4取f分别为 400 N、500 N、600 N;具体如表1所示。
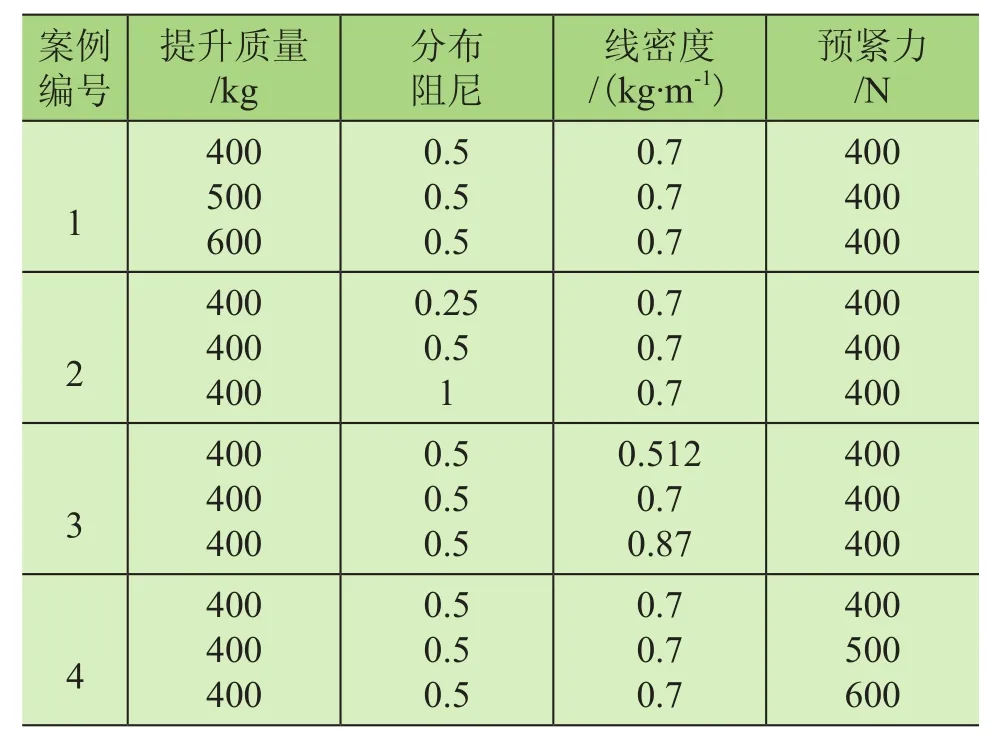
表1 案例分析参数
2.1 提升质量m影响的分析
在案例1中对电梯上、下行过程的振动进行仿真,分析不同单根钢丝绳提升质量m对电梯提升钢丝绳水平方向振动响应的影响。图2~图4为m=400 kg、500 kg、m=550 kg时提升钢丝绳水平方向振动加速度响应曲线。从图可得电梯上行时提升钢丝绳水平方向振动加速度的最大值分别为0.591 4 m/s2、0.75 m/s2、0.766 m/s2;下行时其最大值分别为0.390 3 m/s2、0.406 7 m/s2、0.410 2 m/s2。由图可知,电梯上、下运转过程中,提升钢丝绳水平方向振动加速度响应幅值随提升质量m的增大而逐渐增大,故可以通过减小单根提升钢丝绳的提升质量来减弱提升钢丝绳水平方向的振动。
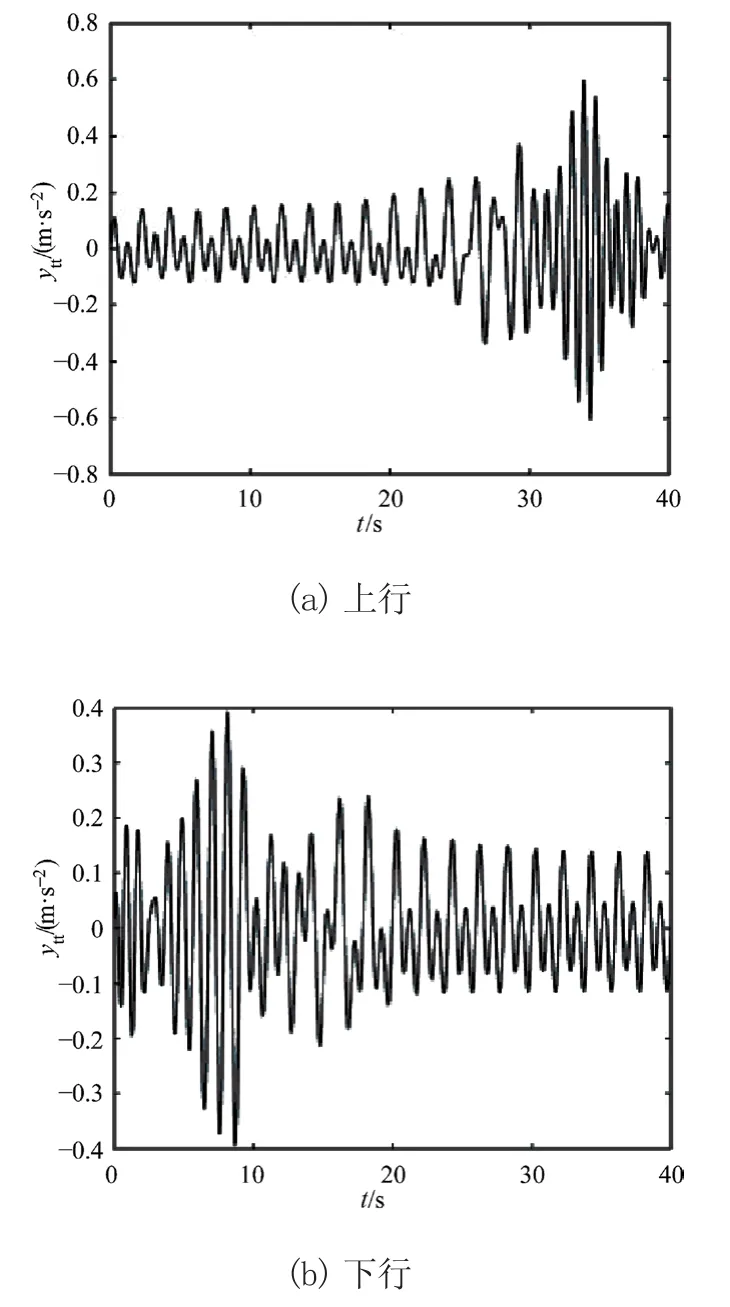
图2 m=400 kg时提升钢丝绳水平方向振动加速度响应
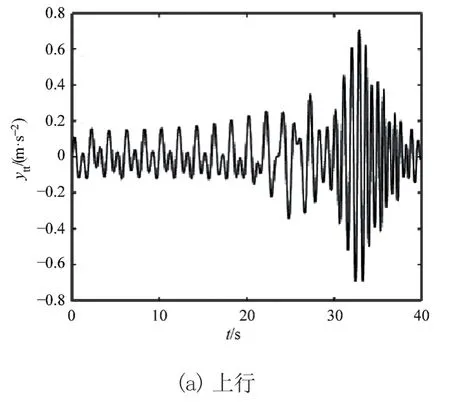
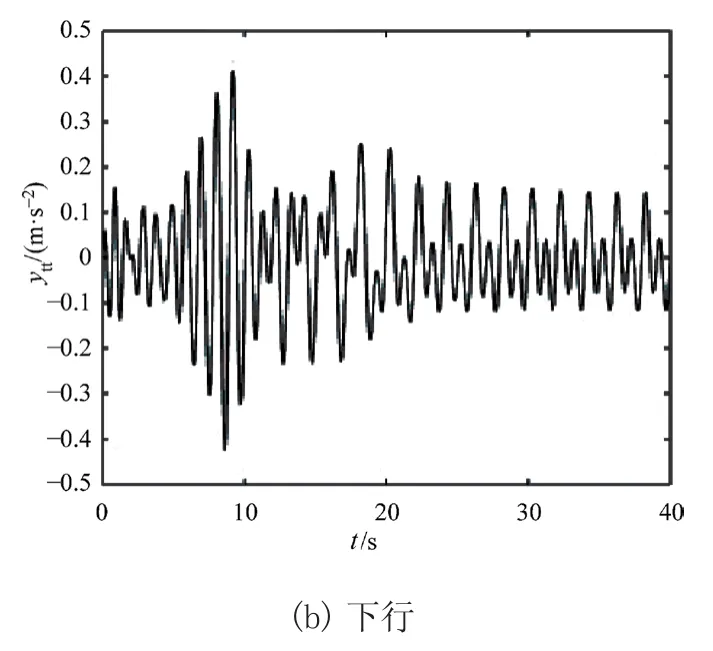
图3 m=500 kg时提升钢丝绳水平方向振动加速度响应

图4 m=550 kg时提升钢丝绳水平方向振动加速度响应
2.2 提升曳引绳分布阻尼的影响分析
在案例2中对电梯上、下行过程的振动进行仿真,分析不同分布阻尼c对电梯提升钢丝绳水平方向振动响应的影响。图5~图7为c=0.25、0.5、1时提升钢丝绳水平方向振动加速度响应曲线。从图可得电梯上行时提升钢丝绳水平方向振动加速度的最大值分别为0.594 9 m/s2、0.574 3 m/s2、0.406 2 m/s2;下行时其最大值分别为0.497 m/s2、0.39 m/s2、0.275 5 m/s2。由图可知,电梯上、下运转过程中,提升钢丝绳水平方向振动加速度响应幅值随分布阻尼的增大逐渐减小,故可以通过增大分布阻尼来减弱提升钢丝绳水平方向的振动。
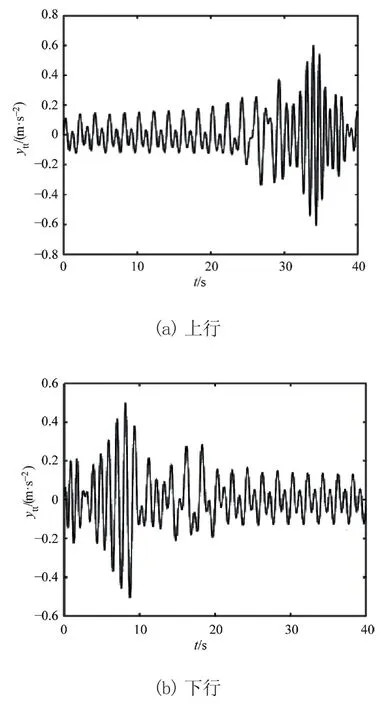
图5 c=0.25时提升钢丝绳水平方向振动加速度响应


图6 c=0.5时提升钢丝绳水平方向振动加速度响应
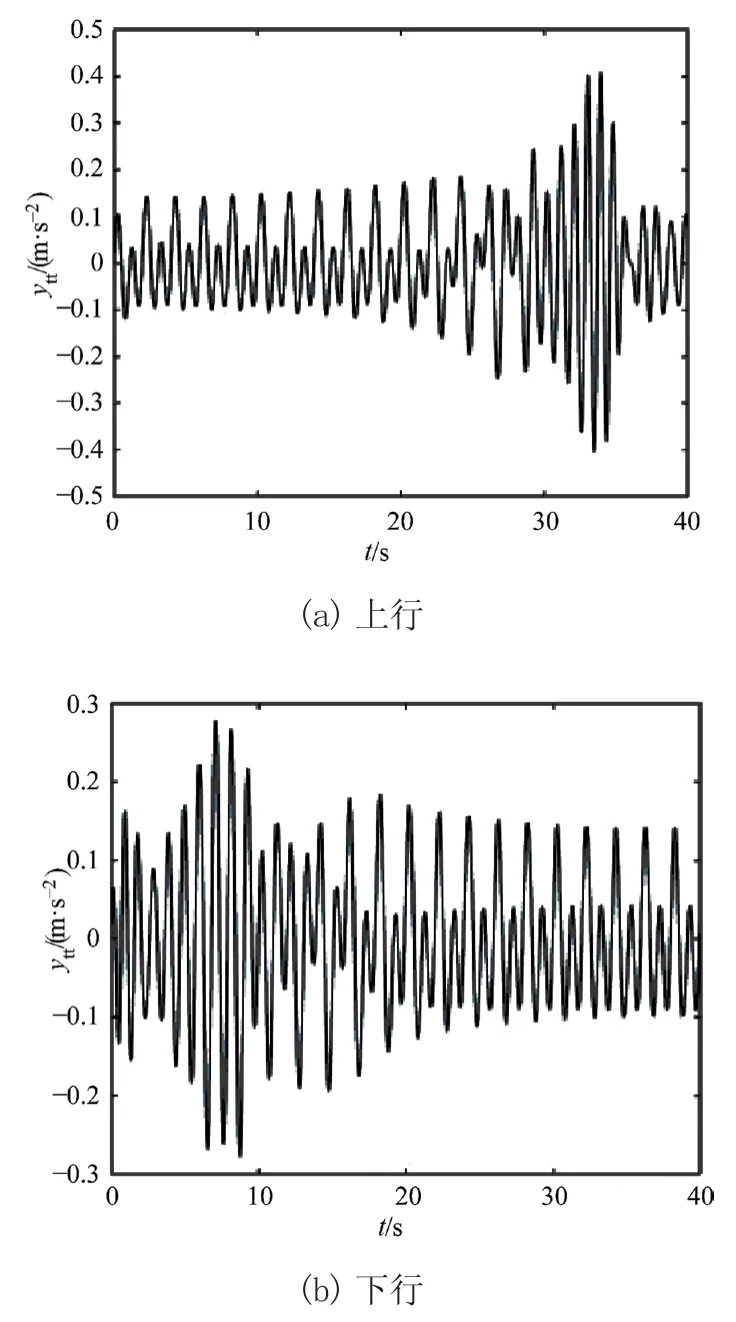
图7 c=1时提升钢丝绳水平方向振动加速度响应
2.3 提升曳引绳线密度的影响分析
在案例3中对电梯上、下行过程的振动进行仿真,分析不同线密度ρ对电梯提升钢丝绳水平方向振动响应的影响。图8~图10为ρ=0.512 kg/m3、ρ=0.7 kg/m3、ρ=0.87 kg/m3时提升钢丝绳水平方向振动加速度响应曲线。从图可得电梯上行时提升钢丝绳水平方向振动加速度的最大值分别为0.553 8 m/s2、0.601 1 m/s2、0.840 9 m/s2;下行时其最大值分别为0.359 2 m/s2、0.388 5 m/s2、0.441 6 m/s2。由图可知,电梯上、下运转过程中,提升钢丝绳水平方向振动加速度响应幅值随线密度的增大而逐渐增大。因此,可以通过减小线密度来减弱提升钢丝绳水平方向的振动。

图8 ρ=0.512 kg/m3时提升钢丝绳水平方向振动响应
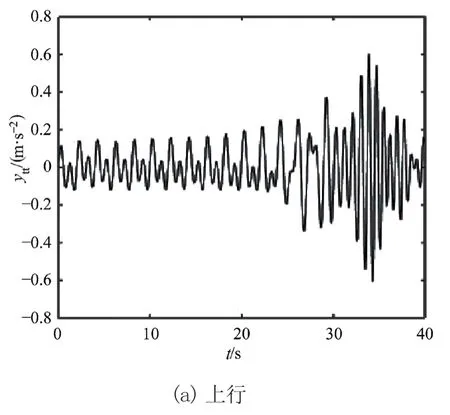
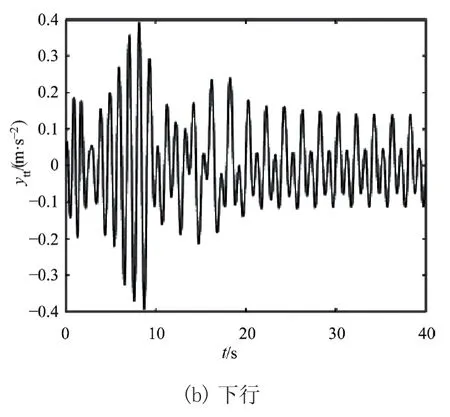
图9 ρ=0.7 kg/m3时提升钢丝绳水平方向振动响应
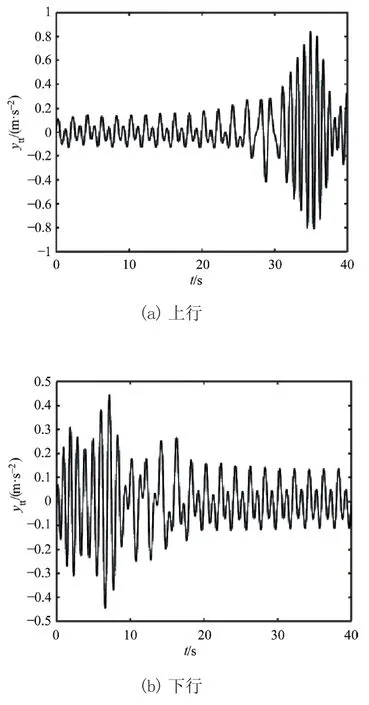
图10 ρ=0.87 kg/m3时提升钢丝绳水平方向振动响应
2.4 电梯预紧力的影响分析
在案例4中对电梯上、下行过程的振动进行仿真,分析不同预紧力f对电梯提升钢丝绳水平方向振动响应的影响。图11~图13为f=400 N、500 N、600 N时提升钢丝绳水平方向振动加速度响应曲线。从图可得电梯上行时提升钢丝绳水平方向振动加速度的最大值分别为0.594 9 m/s2、0.605 2 m/s2、0.621 9 m/s2;下行时其最大值分别为 0.388 3 m/s2、0.392 8 m/s2、0.395 5 m/s2。由图可知,电梯上、下运转过程中,提升钢丝绳水平方向振动加速度响应幅值随预紧力的增大而逐渐增大,故可以通过减小预紧力来减弱提升钢丝绳水平方向的振动。
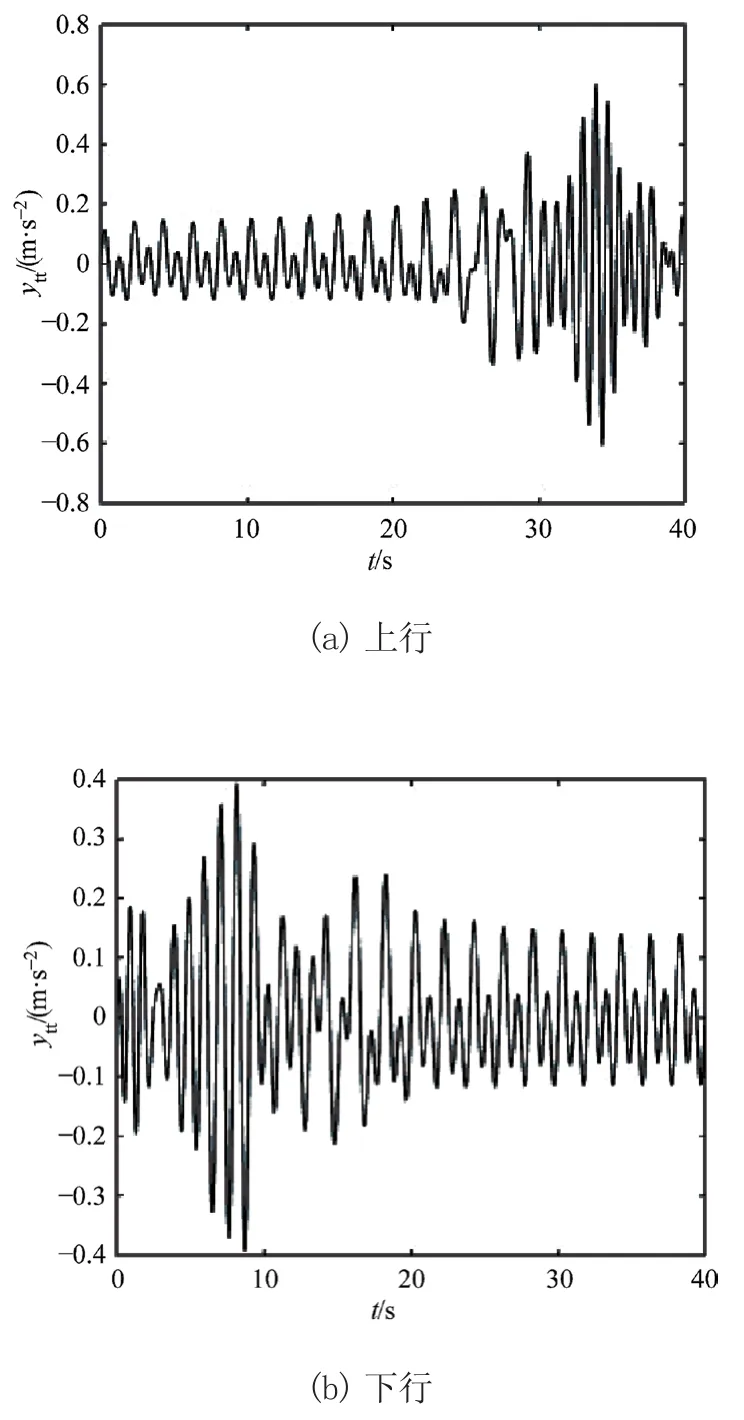
图11 f=400 N时提升钢丝绳水平方向振动加速度响应


图12 f=500 N时提升钢丝绳水平方向振动加速度响应

图13 f=600 N时提升钢丝绳水平方向振动加速度响应
3 结论
1)增大分布阻尼c可以减弱提升钢丝绳水平方向的振动,分布阻尼c和提升钢丝绳水平方向振动响应呈负相关;
2)减少单根提升钢丝绳的提升质量m、钢丝绳线密度ρ、预紧力f可以减弱提升钢丝绳水平方向的振动,单根提升钢丝绳的提升质量m、钢丝绳线密度ρ、预紧力f和提升钢丝绳水平方向振动响应呈正相关。

