基于Logistic-Tent混沌映射和位平面的图像加密算法

秦秋霞，梁仲月，徐 毅

(大连民族大学 a.计算机科学与工程学院；b.理学院，辽宁 大连 116650)

快速发展的互联网在现代生活中发挥着巨大作用。不仅给人们带来简单、便捷的生活方式，同时使人们信息交流畅通无阻。图像信息以其直观、简单的特点已成为传递信息的一种媒介[1]。然而互联网时代具有双面性，给人们的生活带来巨大便捷的同时，图片信息的恶性盗取、传播也会给人们的公众财产带来巨大损失[2-3]。为了保护图像信息，使其在公共信道上能够安全的传输，本文使用新型复合混沌系统结合比特级的扩散、置乱方法实现图像加密。

混沌系统是用来描述确定的非线性系统所产生的对初值条件敏感、非周期性、内部随机性的一种复杂的混沌现象[4-5]。一般情况下，混沌系统分为低维混沌[6]和高维混沌[7]。高维混沌系统结构较复杂，控制参数多，计算的复杂度高[7]。低维混度系统结构简单，控制参数少，易于实现[6]。但也存在一些问题，比如，混沌行为是有限的，混沌区间不连续，生成的混沌序列呈现非均匀数据分布等。为了开发具有更好混沌性能的混沌系统，研究人员将多种低维混沌结合在一起，形成新的复合混沌系统[8-9]，该类混沌系统可以有效克服低维混沌的不足，并且与高维混沌相比，复杂度更低，更易实现。比如，2022年唐等人[8]针对传统一维混沌系统的局限性以及参数值的安全问题，提出一种Logistic-Sine复合混沌映射并将其用于图像加密，取得了良好的加密效果。同年，张等人[9]使用Logistic-Sine-Cosine复合混沌系统生成的混沌序列进行行列置乱和循环像素扩散，保障了算法的安全性。所以，本文使用Logistic混沌映射和Tent混沌映射复合生成的Logistic-Tent混沌映射参与加密过程，提高了加密算法的随机性。

灰度图可以用多个比特位来表示，其中的每个比特位可以用来表示1个二值的平面，也称为位平面[7]。一幅数字图像可以分解为多个位平面，不同的位平面代表不同的图像信息。目前，多数加密算法的置乱、扩散操作是在块、像素级别上进行的，这些算法的加密效果与基于比特级的加密效果相比较差。比如，王等人[10]提出了一种基于分块置乱和混合混沌的图像加密算法，该算法是在块级别上实现的置乱操作。张等人[11]提出了一种结合S盒与混沌映射的图像加密算法，该算法所有的操作都是在像素级上进行的。无论是基于块级别的加密算法还是基于像素级别的加密算法，加密效果与基于比特级别的加密算法相比略差一些。所以，文本提出了一种基于位平面和混沌的图像加密算法，使用位平面的分解以及合并，保证置乱、扩散操作可以在比特级上进行，保证了加密效果，提高了加密算法的安全性。

综上所述，本文提出了一种基于Logistic-Tent混沌映射和位平面的图像加密算法。首先将原始图像分解成位平面，然后将其转化为两个大小相同的二进制序列，然后在Logistic-Tent混沌序列的控制下实现比特级别的置乱和扩散操作，最后进行位平面的合并，得到加密图像，完成加密操作。本文的主要结构如下：第一部分主要介绍本算法使用的基本原理；第二部分介绍加、解密算法的详细设计和基本步骤；第三部分给出仿真结果和安全性分析；第四部分给出结论。

1 基本原理

本章主要介绍本文用到的Logistic-Tent混沌映射，位平面相关原理。

1.1 Logistic-Tent混沌映射

Logistic混沌系统是一个非常典型的一维混沌系统，它虽然结构简单，但却能产生复杂的混沌动力学特性，因此在加密算法中非常常见[6]。Logistic混沌系统的数学定义公式如下：

xn+1=μxn(1-xn)。

(1)

式中：x是系统变量；μ是控制参数；x∈[0,1]，μ∈[3.57,4]。

但Logistic混沌映射也存在一些不足，比如，混沌范围仅存在于μ∈[3.57,4]时，参数的有些取值并不能使得系统产生混沌行为，并且在μ<3.57时，李雅普诺夫指数为负数，如图1；系统参数的值不在[0,1]时，生成的混沌序列不均匀，不适合用于图像加密。

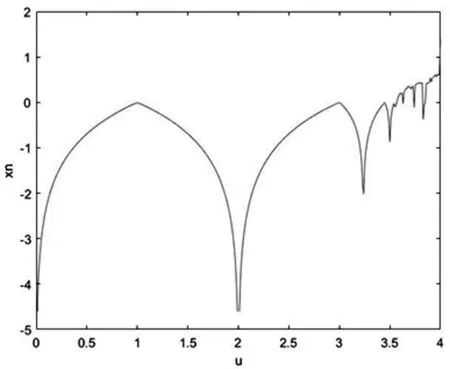
图1 Logistic混沌的李雅普诺夫指数

Tent混沌系统又称为帐篷映射，它是一种分段线性的一维映射，它具有混沌特性，均匀的概率密度和功率谱密度，并且具有比较良好的自相关性[6]。其数学定义公式如下：

(2)

式中：x是系统变量；k是控制参数；x∈[0,1]，当k∈[2,4]时，系统处于混沌状态。同样的，Tent混沌映射也会存在控制参数少，混沌区间有限等问题。

Gupta等人[6]将经典的一维Logistic混沌系统、Tent混沌系统进行集成生成的Logistic-Tent复合混沌系统。该混沌系统融合了Logistic复杂的混沌动力学特性和Tent混沌系统更快的迭代速度、更多的自相关性和适用于大量序列的特点。将该混沌系统引入本加密算法，保证算法的安全性。它的数学公式定义如下：

(3)

式中：X是系统变量；r为控制参数；X∈[0,1]，r∈(0,4)。Logistic-Tent混沌系统在[0,1]的分岔图如图2。

图2 Logistic-Tent混沌分岔图

从图2可知，当X∈[0,1]范围内时，其输出序列均匀分布，远比Logistic、Tent映射在此范围内的混沌特性更加突出，因此说明该混沌系统比Logistic混沌系统和Tent混沌系统拥有更好的混沌性能。

1.2 位平面

把灰度图中处于同一个比特位上的二进制像素值进行组合，得到的一幅二进制图像称为灰度图的一个位平面[7]。在灰度图中，像素值的范围是[0,255]，一个像素值可以用8位二进制序列表示。最后，使用二进制位平面分解就可以将灰度图分为8个二进制位平面。第i个位平面包含灰度图中每一个像素序列的第i个比特值，其中i∈[0,8]。对测试图像Tank进行位平面分解后，得到的每个位平面的视觉效果如图3。

图3 位平面分解图

从图3中的位平面分解图可以看出，灰度图的第5～8位高位位平面，呈现的效果较好，接近于原始图像。而第1～3位的低位位平面接近黑白色，与原始图像的信息相差较大。本文将位平面的分解与合并运用到加密算法中，可以实现比特级的置乱、扩散，提高了加密算法的随机性。

2 加解密算法

本文提出了一种基于Logistic-Tent混沌映射和位平面的图像加密算法。首先，将原始图像进行位平面的分解，分解的各个位平面转化成行向量；然后，Logistic-Tent混沌映射使用密钥1多次迭代生成混沌序列，将混沌序列也转化成行向量，两种方式生成的行向量使用循环移位和按位异或进行扩散操作；然后，使用密钥2再次迭代Logistic-Tent混沌映射,生成的混沌序列用来控制两种序列的交换过程，实现置乱操作；最后，将置乱后的序列转换为位平面，各个位平面合并生成加密图像。具体的加密步骤如2.1～2.5节所示。加密流程图如图4。

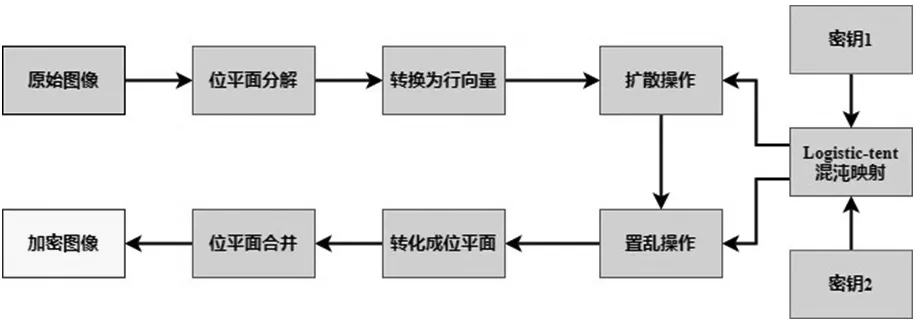
图4 加密流程图

2.1 位平面的分解

位平面的分解主要包括原始图像P的位平面分解以及Logistic-Tent混沌序列的位平面的分解，具体如下：

第一步：读入原始图像P，将原始图像P使用二进制取余法分解为1～8位位平面，如下所示：

p1=mod(P,2);

p2=mod(floor(P/2),2);

p3=mod(floor(P/4),2);

p4=mod(floor(P/8),2);

p5=mod(floor(P/16),2);

p6=mod(floor(P/32),2);

p7=mod(floor(P/64),2);

p8=mod(floor(P/128),2)。

其中，floor()是向下取整函数，mod()是取余函数。

第二步：将高位位平面组合生成矩阵A1,低位位平面组合生成矩阵A2，其中A1和A2的大小都为4MN，两个矩阵将参与后续扩散操作，生成过程如下：

A1=[p1,p2,p3,p4],

A2=[p5,p6,p7,p8]。

第三步：使用密钥1中的x0和μ0作为Logistic-Tent混沌映射的初值和控制参数，多次迭代生成大小为MN的混沌序列seq1，由于像素值的范围是[0,255]，需要对得到的混沌序列seq1进行如下处理：

seq1=mod(floor(seq1×1014),256)。

其中，floor()是向下取整函数，mod()是取余函数。

第四步：将第三步生成的混沌序列seq1使用二进制取余法也进行位平面的分解，具体如下：

s1=mod(seq1,2);

s2=mod(floor(seq1/2),2);

s3=mod(floor(seq1/4),2);

s4=mod(floor(seq1/8),2);

s5=mod(floor(seq1/16),2);

s6=mod(floor(seq1/32),2);

s7=mod(floor(seq1/64),2);

s8=mod(floor(seq1/128),2)。

其中，floor()是向下取整函数，mod()是取余函数。

第五步：将混沌序列分解生成的位平面进行分组，高位位平面组合生成矩阵B1，低位位平面组合生成矩阵B2，B1和B2的大小都为4MN，具体如下：

B1=[s1,s2,s3,s4]，

B2=[s5,s6,s7,s8]。

2.2 扩散操作

本文使用循环移位和按位异或实现扩散操作，具体如下：

第一步：使用A2矩阵像素值之和作为循环移位的位数，为第一次循环移位操作做准备，具体如下：

sum1=sum(sum(A2))。

其中，sum()求和函数，此处输入的是矩阵，所以求得结果是矩阵所有元素之和。

第二步：对矩阵A1进行循环移位操作，具体如下：

A11=circshift(A1,sum1,2)。

其中，circshift()函数是循环右移函数，第一个参数表示待移位的矩阵，第二个参数表示移位数，第三个变量等于1时表示列移位，第三个变量等于2时表示行移位。

第三步：第二步生成的A11与A2矩阵、B1矩阵进行按位异或操作，得到序列C1，实现了像素值的改变，具体如下：

C1(1)=((A11(1)⊕A11(4MN))⊕A2(1))⊕B1(1)。

C1(i)=((A11(i)⊕A11(i-1))⊕A2(i))⊕B1(i)，i=2,…,4MN。

其中，⊕是按位异或操作。

第四步：使用第三步得到的C1继续生成第二次循环移位的移位数sum2，具体如下：

sum2=sum(C1)。

其中，sum()求和函数,此处输入的是一个序列，所有得到的结果就是序列的所有元素之和。

第五步：对矩阵A2进行循环移位操作，具体如下：

A22=circshift(A2,sum2,2)。

其中，circshift()函数是循环右移函数，第一个参数表示待移位的矩阵，第二个参数表示移位数，第三个变量等于1时表示列移位，第三个变量等于2时表示行移位。

第六步：将第五步生成的A22与序列C1、矩阵B2进行按位异或操作，得到序列C2，具体如下所示：

C2(1)=((A22(1)⊕A22(4MN))⊕C1(1))⊕B2(1)，

C2(i)=((A22(i)⊕A22(i-1))⊕C1(i))⊕B2(i)，i=2,…,4MN。

其中，⊕是按位异或操作。

2.3 置乱操作

使用另一组密钥迭代Logistic-Tent混沌映射，生成混沌序列用来控制C1和C2序列的交换过程，实现置乱操作。

第一步：使用C2序列对密钥2中的初值xx0进行更新，具体如下：

xx0=mod(xx0+(sum2+sum(C2))/4MN,1)。

其中，sum()是求和函数，mod()是取余函数。

第二步：使用更新后的xx0以及密钥2中的μμ0作为Logistic-Tent混沌映射的初值和控制参数进行多次迭代，生成大小为8MN的seq2混沌序列。

第三步：将混沌序列seq2分为s1和s2两个混沌序列，各个混沌序列大小都为4MN，具体如下：

s1=seq2(1:4MN)；

s2=seq2(4MN+1:8MN)。

第四步：因为要使用s1和s2交换C1序列和C2序列的各个元素的位置，C1和C2大小都是4MN，所以需要对s1和s2做进一步的处理，对应地生成Y和Z序列。具体如下：

Y=mod(floor(s1*1014),4MN)+1，

Z=mod(floor(s2*1014),4MN)+1。

其中，floor()是向下取整函数，mod()是取余函数。

第五步：使用Y和Z来交换C1序列和C2序列各个元素的位置，主要包括两轮交换。首先使用Y来控制位置的交换，然后再使用Z控制位置的交换，如下所示：

[C2(Y(i)),C1(i)]=deal(C1(i),C2(Y(i)))，

i=1,…,4MN，

[C1(Z(j)),C2(j)]=deal(C2(j),C1(Z(j)))，

j=1,…,4MN。

其中，此处的deal()函数具有将两个参数分别赋予两个对应变量的作用。

2.4 位平面的合并

将C1和C2序列首先转化成矩阵，然后将各个矩阵转换成4个大小为MN的矩阵，也就是各个位平面，然后将位平面合并，生成加密图像C。

第一步：将C1和C2序列分别转换成成4MN的矩阵CC1和CC2，如下：

CC1=reshape(C1,M,4N)，

CC2=reshape(C2,M,4N)。

其中，reshape()函数是矩阵重组函数。

第二步：将CC1、CC2矩阵分别生成4个MN大小的数组，如下：

E1=mat2cell(CC1,M,[N,N,N,N])，

E2=mat2cell(CC2,M,[N,N,N,N])。

其中，mat2cell()函数就是将矩阵转化成胞元数组。

第三步：将E1和E2中的各个数组转化成矩阵，也就是各个位平面，提取出各个位平面c1、c2、c3、c4、c5、c6、c7、c8。

第四步：使用二进制取余法的逆操作，将各个位平面进行合并，生成加密图像C，加密完成。

2.5 加密算法

具体的加密步骤如下：

(1)原始图像以及Logistic-Tent混沌序列使用二进制取余法进行位平面的分解，高位位平面和低位平面组合分别生成2个矩阵，如2.1节所示。

(2)原始图像位平面分解后生成的矩阵和混沌序列位平面分解后的矩阵进行循环移位操作以及按位异或操作，使得像素值发生改变，完成扩散操作，如2.2节所示。

(3)使用密钥2再次迭代Logistic-Tent混沌生成混沌序列，用来交换扩散后得到的序列的各个元素的位置，使得像素值的位置发生改变，完成置乱操作，如2.3节所示。

(4)将置乱后生成的序列转换成矩阵，并提取各个位平面，最后将各个位平面进行合并，生成加密图像，如2.4节所示。

2.6 解密算法

解密算法和加密算法是互逆的关系。在加密算法中，需要进行位平面分解、扩散、置乱、位平面合并操作。但在解密算法中需要注意各个操作的顺序，应该先进行位平面分解，置乱的逆操作，扩散的逆操作，位平面的合并，才能完成解密过程。其他类似，不再详细介绍。

3 安全性分析

在Window 10操作系统下，Matlab R2020a软件中进行仿真实验。该实验主要是对三组不同大小的灰度图像进行加密、解密实验。本实验中使用的具体的密钥信息见表1。256×256大小的Tank原始图像、加密图像以及解密图像如图5。512×512大小的Cat原始图像、加密图像以及解密图像。1024×1024大小的Airplane原始图像如图6，加密图像以及解密图像如图7。

表1 密钥展示表

a) Tank原图 b) Tank密图 c) Tank解密图图5 Tank图的加密、解密效果

a) Cat原图 b) Cat密图 c) Cat解密图图6 Cat图的加密、解密效果

a) Airplane原图 b) Airplane密图 c) Airplane解密图图7 Airplane图的加密、解密效果

通过图5～7的加密、解密的效果图可以看出，本算法得到的密图十分模糊，丝毫看不出原图的任何信息，得到的解密图和原图相对比，在视觉上看不出差异，见表2。同时通过表2也可以看出，原图和解密图的相似度高达99.999%，说明解密图像和原始图像的差别在可接受的范围内，基本上可以忽略不计。以下各个章节对于安全性能的分析，均以Tank图为例。

表2 原图、解密图相似度分析表

3.1 密钥空间

密钥空间指加密密钥的大小，加密密钥要足够大才能够有效的抵抗穷举攻击[12]。随着计算机设备不断地发展，一次攻击使用的时间越来越短，占用资源越来越少。目前，当密钥空间大于2时100[13]，加密算法才能处于相对稳定的状态。

通过表1可以看出，本算法的加密算法主要分为两部分。密钥1是在扩散操作时使用的密钥，其中包括2个密钥。密钥2是在置乱操作时使用的密钥，其中也包括2个密钥。当计算精度为1014时，本加密算法的密钥大小是(1014)4=1064。本算法的密钥空间在数值上大于2100，说明该算法密钥空间足够大，可以有效抵抗穷举攻击，保障了加密算法的安全性。

3.2 信息熵

信息熵是图像评价的一个衡量标准，它指的是图像信息的相对复杂性[14]。灰度值平均分布的图像信息熵也比较大，当各个灰度值等概率分布时，信息熵能够达到最大值。信息熵的数学表达式如下：

(4)

式中：m表示灰度图像；H(m)表示灰度图像的信息熵；mi表示L灰度级图像m的第i个灰度值；P(mi)表示mi出现的概率。理想情况下，随机图像的信息熵为8[15]。原始图像和加密图像的信息熵对比情况，见表3。

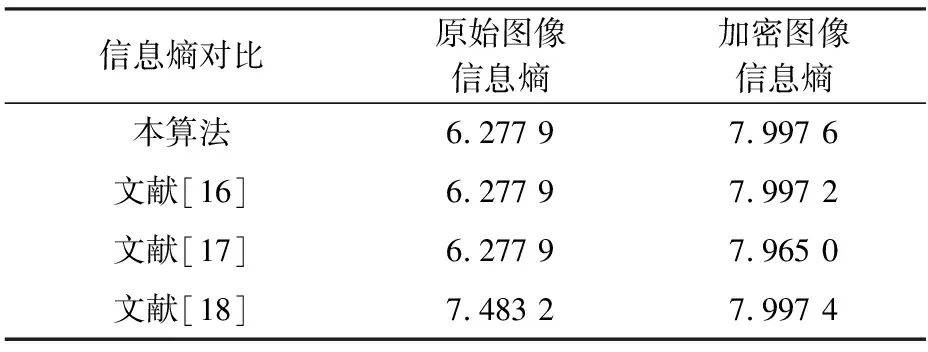
表3 原图和密图信息熵对比表分

通过表3可以看出，首先，本算法可以使得信息熵较低的原图经过加密算法变成信息熵接近于理想值的密图，提高了算法的随机性和安全性。其次，通过与各个算法对比，本算法的信息熵值略高于文献[16],文献[17]，与文献[18]相近。说明本算法可以有效地增大图像的信息熵值，与其他算法相比具有一定的优越性。

3.3 相关性

相关性强是原始图像的固有属性，这种强相关性能够传递出原始图像的信息[15]。加密算法的目的就是打破这种强相关性得到反映不出原始图像信息的加密图像。在理想情况下，相关性应该尽可能的接近于0[8]。相关性系数的计算公式如下：

(5)

(6)

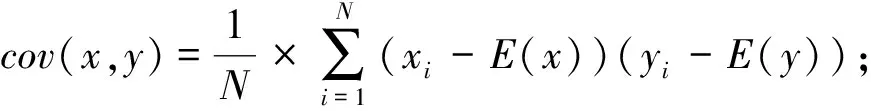
(7)

(8)

式中：x和y是图像的像素值；E(x)是期望值；D(x)是方差；cov(x,y)是协方差；rxy是相关性系数。

这一小节从两个方面来分析使用本加密算法得到的密文图像的相关性。一是定量分析，给出加密前后水平、垂直、对角线方向的相关系数值。本文选取2000对相邻的像素点用来计算相关性数值，实验结果见表4。

表4 原图和密图相关性系数对比表

从表4数据可以看出，明文像素相关性系数和密文相关性系数存在很大差异，明文3个方向相关性系数接近于1，说明像素之间存在极强的相关性。而密文图像3个方向相关性系数接近于0，说明加密过程削弱了明文图像的相关性，能够很好的隐藏明文图像信息，能够达到良好的加密效果。并且与其他最新文献相对比情况来看，本算法性能也比较好。

二是定性分析，从直观上绘出了三个方向像素对的分布情况，如图8～9。

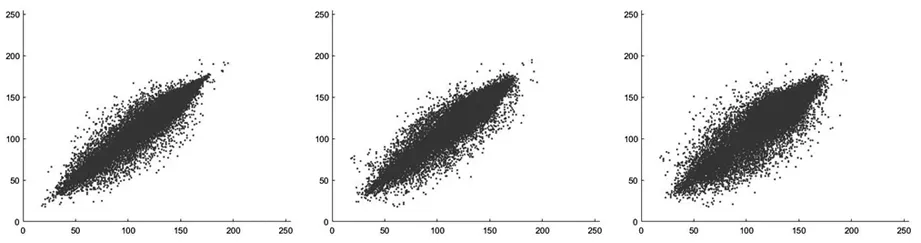
a) 原图水平 b) 原图垂直 c) 原图对角线图8 原图相关性点图

a) 密图水平 b) 密图垂直 c) 密图对角线图9 密图相关性点图

从图8、图9可以看出，明文图像3个方向的相邻像素对基本上都是处于象限对角线两侧，这说明相邻像素对的值非常相似，也就是说像素对具有强相关性。但是加密后图像三个方向的相邻像素对都是均匀分布在坐标区域X轴和Y轴的象限区域内，这说明这些相邻像素对的值不同，相关性低。综合相关性系数表和相关性图来看，本加密算法具备良好的抗统计攻击的能力。

3.4 直方图

图像的直方图用来分析一个图像像素分布的情况。图像信息都是由像素构成的，所以用来分析图像像素分布的直方图是衡量图像的一种重要特性[5]。原始图像的直方图，加密图像的直方图，解密图像的直方图具体如图10。

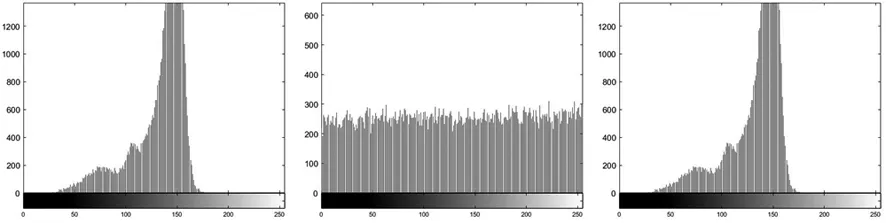
a) 原图直方图 b) 密图直方图 c) 解密图直方图图10 原图、密图、解密图的直方图分布

从图10可以看出，由于原始图像是存在特殊意义的图像，所以像素分布在中间灰度范围内较集中，总体分布高低不平，统计性信息明显。加密图在[0,255]灰度范围内基本上是均衡分布的，统计特征被很好地掩饰。解密图的直方图与原始几乎是100%相似，说明本算法可以解密出有效图像。

3.5 时间性能分析

一个性能优越的加密算法，除了能够得到良好仿真结果图，具备足够强大的安全性之外。还要保证能够在有效的时间内得到加密图、并且在较短时间内能够实现快速解密[3]。本小节对3组不同尺寸大小的图像进行加解密的时间测试，具体见表5。

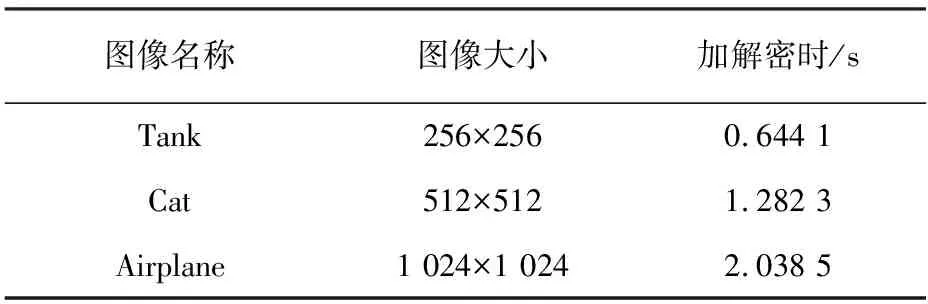
表5 时间性能对比表

从表5数据看出，本算法不仅能够对不同尺寸大小的图片进行加解密，而且加解密能够控制在非常短的时间内，说明本算法在时间性能方面也比较优越。

4 结 语

本文提出了一种基于Logistic-Tent混沌映射和位平面的图像加密算法。Logistic-Tent混沌系统结合位平面的操作，实现了比特级的置乱和扩散操作。从仿真结果和安全性分析来看，本算法不仅具有良好的加密、解密效果，而且密钥空间足够大，安全性也能够得到保障。另外，本算法具有一定的时效性，能够在较短时间内对不同尺寸的图像实现快速的加密、解密操作。以上说明本算法非常适用于图像加密。