化归与转化思想在数学教学中的作用探讨

邓玉兰

化归与转化思想在数学教学中的作用探讨

邓玉兰

（兰州市第六十一中学，甘肃兰州730060）

化归与转化是一种重要的数学思维方式，甚至是其他数学思想方法的核心。掌握了化归与转化思想，不但能够引导学生更好地学习数学知识、解决数学问题，还能够使学生在其他学科的学习和生活实际问题的解决中得心应手。

化归与转化思想；数学教学；作用

数学思想是数学活动中“教与学”的灵魂，作为建立和运用数学解决问题的指导思想，它指引着学习者和教学者顺利完成在数学“教与学”中的各项工作和任务。由于数学领域的问题千姿百态，所以衍生出了多种不同的数学思想方法，用于指导数学知识的教与学。

一、化归与转化思想简介

化归与转化思想就是这五彩缤纷的数学思想方法世界中最耀眼的一颗星，钱佩玲老师也称化归与转化思想是数学中问题解决的基本方法。首先化归与转化思想符合学生的认识规律；其次数学学科自身的特点和数学科学的哲学基础，决定了化归与转化思想的数学地位——数学解决问题的基本方法。

“化归”一词其实就含有转化的意思，但是，其最终目的是将一个问题归结为另外一个方便于解决的问题。基本思想是：在数学问题的解决过程中，人们通常会把需要解决的问题M，经过某种转化的方法，将其变换为另外一个已经解答或者已经有固有的解决程序的数学问题N，并且通过解决问题N，进而可以解决原问题M。这样一个化归的过程通常可以用下面的框图简单表示：

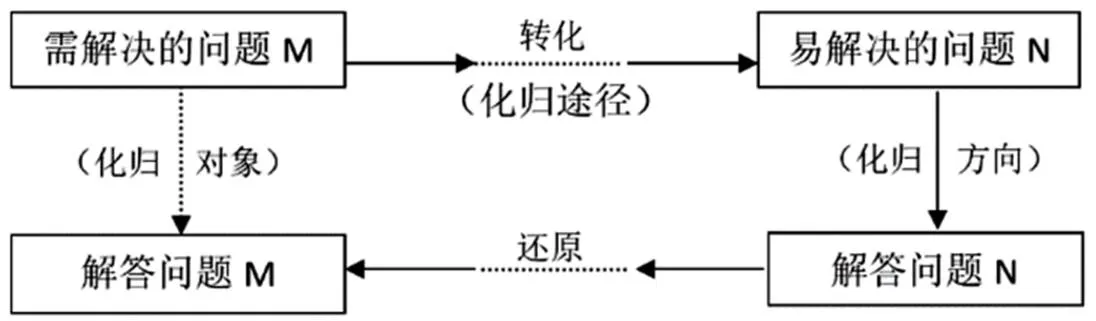
图1

如图1中标示的，问题N经常被称作化归与转化的方向或目标，化归与转化的方法就是转化，经常被称作化归与转化的策略。化归的方向有时可能是将烦琐的问题化成单一的问题，有时是将未知的问题化成已知的问题，有时是将不能解答的问题化成已经解答的问题等，有时并不是一步就能完成化归与转化，需要经过好几步才能完成。也就是说将原来的问题M，通过转化途径，转化为问题M1，再将问题M1转化为问题M2，按照“化难为易，化繁为简，化未知为已知”的基本原则继续进行转化，直至将其转化为问题N，然后一步一步地还原解答每一个问题，直至解答原问题M。如此一来，上面框图又可以呈现为更一般的化归模式，图2：

图2

由此可以看出化归与转化思想符合“小步子教学”的原则，把较复杂难以解决的问题，不如就称其为“大问题”，转化为一个个比较容易解答的“小问题”，各个击破，最终回归到原问题，解决一开始的“大问题”。也有人将化归与转化思想称为是一种“迂回前进”的方法，而其最终的目的是“回到老家”，解答原始的问题。

据说，从研究数学思想方法中可以看出一个重要的问题，那就是与一般的科学家（如化学家）相比，数学家具有其特殊的地方，那便是在数学思想方法这一方面，因为数学家具有重要的思维特点——他们善于利用化归与转化的思想解决问题。这也就更加突出了，化归与转化思想方法在数学思想方法中的重要地位。

二、化归与转化思想在数学教学中的作用

在数学教学的每一个阶段、每一个环节化归与转化思想都具有指导意义，并且是众多数学思想方法的基础，比如说数形结合思想、函数与方程思想、一般与特殊的思想等。其在中学数学中的主要作用有：

1.运用化归与转化思想指导新知识的形成

比如《分数乘整数》《两平行线间距离公式》的可以用等价转化法去讲解，《集合的基本运算》《平明向量的坐标表示及坐标运算》的讲解可以充分地利用数形结合的思想讲解等，这些案例都体现了化归与转化思想对新知识形成的指导作用。

2.利用化归与转化思想引导问题的解决

问题解决是数学“教”与“学”活动的核心，新知识的讲解也是为问题的解决提供依据和新的方法。化归与转化思想其实是通过转化的方法，将未知的问题转化为已知的问题，将陌生的问题转化为熟悉的问题，将烦琐的问题转化为单一的问题等。转化的方法也是多种多样，比如，数形结合法、特殊化的方法、正反转化的方法等。但是方法再多，其核心的思想就是简化问题，不要用静止的态度看待问题，而是要用变化的态度看问题，学会变通。

师：复合函数求值域，不做变换直接求比较复杂。观察到根号下的内容是二次式，可以联想到配方法，进行相应的转化后大家再观察该式。

生：

师：很好，还可以继续转化吗？想一想两点间的距离公式。

生：

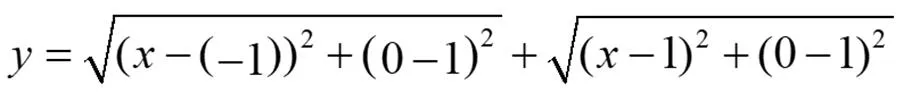
生：解：因为

师：很好，这道题的主要思想是数形结合，通过换元法把函数的值域问题转化为动点到定点的距离和的最值问题。

利用化归与转化思想的熟悉化原则、简单化原则以及和谐化原则解数学题，能够引导学生进行正确的思维活动，使之能够顺利解决问题。

3.利用化归与转化思想进行知识结构的梳理

每次学完一节或一章内容的时候，都应进行知识点的梳理和总结。梳理过程中可以消化、提炼、整理知识，系统化地记忆知识，把零零碎碎的知识组织成井然有序的、层次分明的知识地图，将课本知识学薄，提纲挈领，更容易记忆、理解和利用。

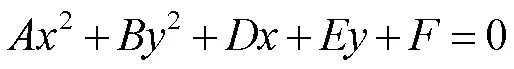
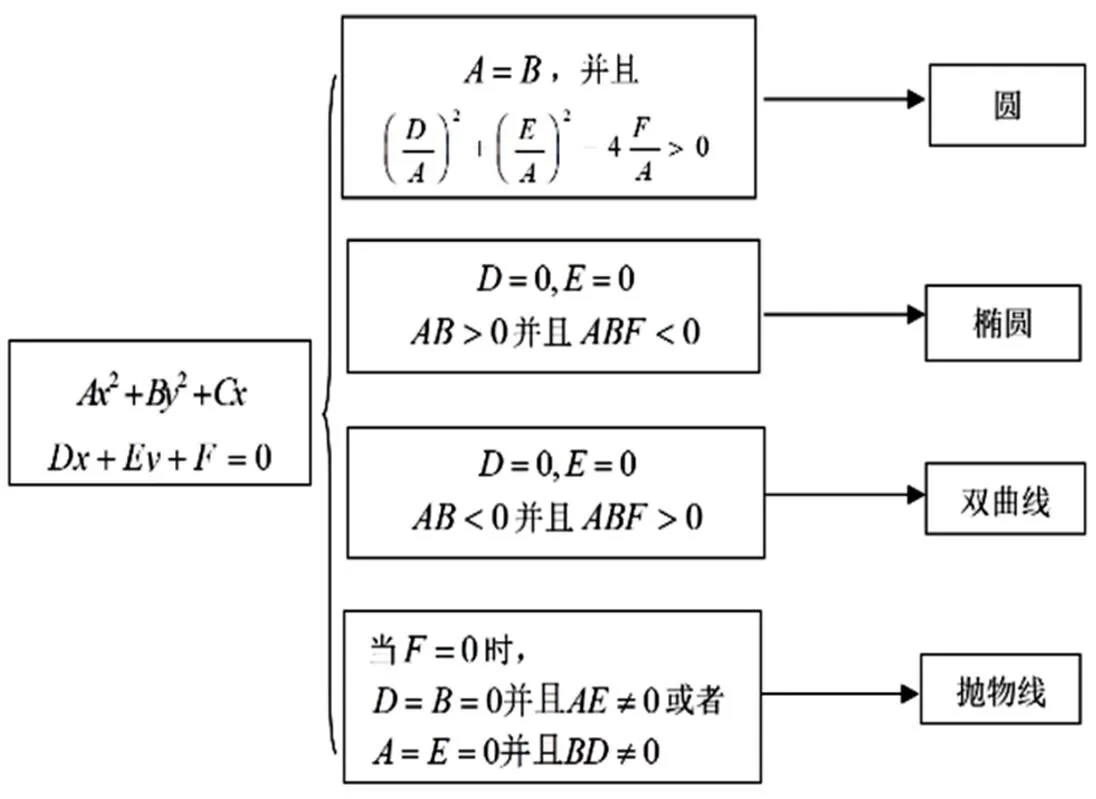
图3

三、在数学教学中进行化归与转化应该注意的问题

化归与转化思想作为问题解决的基本方法，其进行转化的方法可谓是多种多样。恩格斯和马克思的辩证唯物主义告诫后人：“世界永远都是处于运动与变化之中的，要用辩证的态度去看待一切。”所以在利用化归与转化思想的时候，不能将思维局限于某一具体的方法，而是要用动态变化的观点分析问题、解决问题。在化归与转化的过程中应该注意：

1.有目的、有意识地介绍和突出化归与转化，找准目标

有目的、有意识地介绍和突出化归与转化，紧紧“锁住”目标，利用化归与转化的原则，将题目化生为熟，化难为易；进行规范化、高效化的化归与转化。

在教学中，首先，教师应该根据学生的数学学习和教学内容，考虑突出介绍化归与转化思想环节，学生把握化归与转化思想的层次。其次，对每一个教学环节要合理的设计，精心的安排，有意识、有目的地进行化归与转化的教学。

化归与转化思想包括化归与转化的对象、目标以及途径和方法（如图4）。因此，在化归与转化的过程中，应该明确化归与转化的对象，找准化归与转化的目标，选择适当的化归与转化的途径。目标是指引化归与转化前进的关键所在，所以要选准化归与转化的目标。选目标总是基于学生已有的数学知识进行的，根据学生已有的规范性知识，将学生遇到的问题规范化。除此之外，化归与转化能否顺利进行还依赖于化归与转化的方法是否选择的恰到好处，即要同时考虑目标和方法的可操作性、合理性和规范性。在解题的过程中紧紧地锁住目标——原问题的解决，才能选择合理恰当的方法，从而避免盲目地选择方法，致使无法顺利地完成问题的解答。

图4

2.有计划、有步骤地进行化归与转化，注意化归与转化的等价性

化归与转化大体上可以分为等价和非等价的化归与转化，但是中学阶段的化归与转化大多数是等价转化。因此在转化的过程中要注意化归与转化的等价性。数学思想方法的教学是一个循序渐进的过程，在以上的案例中也有所体现，每一阶段对于学生掌握化归与转化的水平要求是不一样的，所以教学的过程中教师应该有计划、有步骤地进行该思想方法的教学，而学生在学习的过程中应该花费时间实践，不断探索化归与转化思想暗含的玄机。

3.注意化归与转化方法的多样性，设计合理方案，选择最佳的方法

化归与转化的方法多种多样，对于同一个问题就可以用多种不同的途径实现，但并不是所有的方法都能简化问题的解决方案，可能反而会使问题更加烦琐，无论如何其中总有使问题最简化的一种方法途径，所以选择最佳的方法是必要的。比如说下面的例题：

（A）点有两个（B）点有四个

（C）点不一定存在（D）点一定不存在

解法二：由图可知，

不可能，所以选。

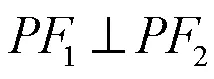
作为一名数学教师，应该加强训练自己利用数学思想方法进行教学的能力，提高对数学思想方法的教学。在备课的时候应该丰富自己的教学目标，将数学思想方法的教学一并列入教学过程中，以辅助数学知识的讲解。只有让学生把握数学思想方法的真谛，才能将数学知识更好地纳入自己的知识体系，加强自己的数学能力，终身受益，而作为教师也才能真正地做到“授学生以渔”。

[1] 钱佩玲.中学数学思想方法[M].北京:北京师范大学出版社,2010.

[2] 赵小云,叶立军.数学化归思维论[M].北京:北京科学出版社,2005.

[3] 朱广俊.化归思想及其在数学教学中的应用[J].江苏第二师范学院学报(自然科学),2014,30(5):18-21.

[4] 袁健.化归思想在初中数学教学中的运用[J].新课程,2010(10):28

[5] 朱成杰.数学思想方法研究导论[M].上海:文匪出版社,1998(6).

[6] 鲍怡.化归思想方法在中学数学教育中渗透的案例研究[D].苏州:苏州大学,2009.

B038

A

1002-7661(2022)15-0058-03