基于集中参数模型的滚动轴承故障研究

郑秀丽，王辉

（浙江工贸职业技术学院，浙江 温州 325003）

0 引言

轴承故障产生的振动信号已经得到了广泛的研究，拥有非常强大的诊断技术[1]。近年来基于人工智能（AI）和机器学习的故障诊断系统已成为一个研究热点，但在轴承故障检测和状态监测领域中如何最有效地应用智能算法，一直是跨界研究的障碍[2]。当前许多学者尝试基于多体轴承动力学模型的分析研究，Fukata等[3]早期学者分析和研究了滚动轴承的基于非线性刚度的动态建模理论，并被Sawalhi等[4-5]改进成五自由度轴承座模型，用于装有轴承的齿轮组件故障模拟和轴承扩展故障引起振动的仿真。Patil等[6]使用滚动轴承的六自由度建模来构建声发射模型。在研究滚动轴承非线性多体动力学分析模型时，大多数的学者均遵循经典的赫兹弹性理论将系统的各种元件或部件模拟为一系列弹簧和阻尼器，用于预测轴承、轴承基座和转子轴承系统振动响应[7]。

为了便于开发实际系统中滚动元件轴承的诊断和预测技术，有必要建立仿真模型[8]，在此模型下可以实现不同的操作条件下故障的仿真，而不是等待这些故障的发生，或者只在实验室下进行测试。通过这些仿真模型产生的故障仿真信号，其中具有明确的特征信号在机器诊断和预测中是非常有价值的[9-12]。

1 六自由度滚动轴承模型

滚动轴承是当前设备最常用的零件，其内部结构及载荷分布如图1所示，其主要包含4个主要部件：内圈、外圈、保持架和滚动体，中心承受着径向力载荷Fr。将正常滚动轴承构建成具有6自由度的参数模型。参数mi、ci和ki分别是内圈的质量、等效阻尼和轴承刚度，同样其它参数如mo、co、ko和mr、cr、kr分别是外圈和保持架的相关参数。其中xi和yi、xo和yo、xr和yr分别是内圈、外圈和保持架在x和y两个方向的相关位移。根据牛顿第二定律得滚动轴承集中参数模型的六自由度等式为：

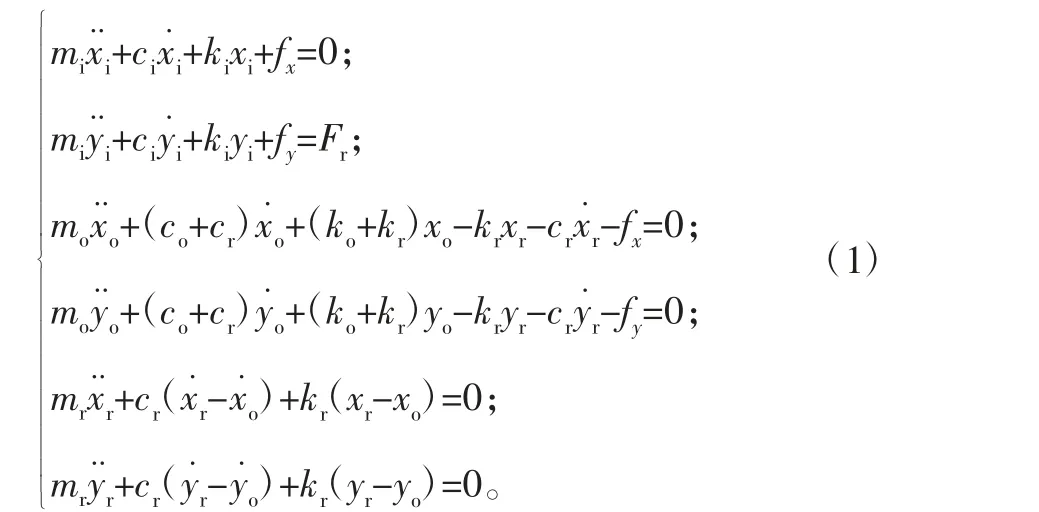
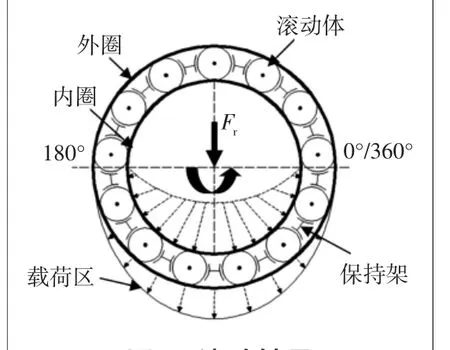
图1 滚动轴承

2 轴承外圈局部故障模型创建与分析

2.1 外圈局部故障模型创建

滚动轴承使用时，大部分机构是利用内圈紧配轴承转动，少部分是外圈带载荷转动，但外圈带载荷转动时由于带动滚珠的线速度大，故轴承的寿命减少约1/3[8]。如图2所示，当外圈存在故障时，由于故障点跟随外圈固定于轴承座上，因此故障点相对于原点0°的相对角位置角φd是不变的。

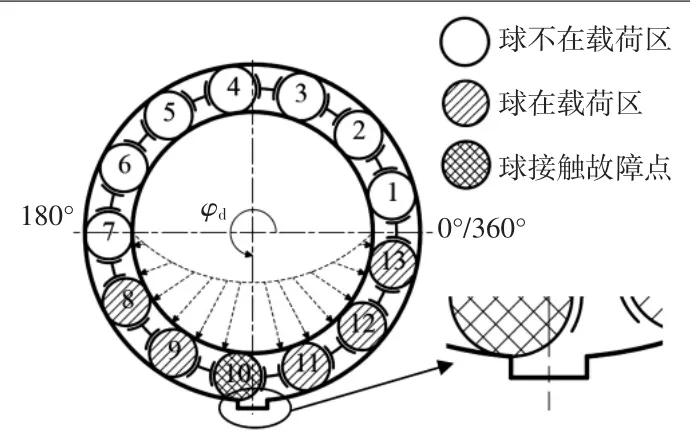
图2 外圈带故障的滚动轴承

将缺陷Cd的深度重新定义为相对角位置角φd的函数。图3所示为外圈故障点局部放大图，展示了滚动体进入缺陷→到达缺陷中心位置→离开缺陷的过程，球进入缺陷Cd深度是随着球的位置而变化。则缺陷Cd表示为：

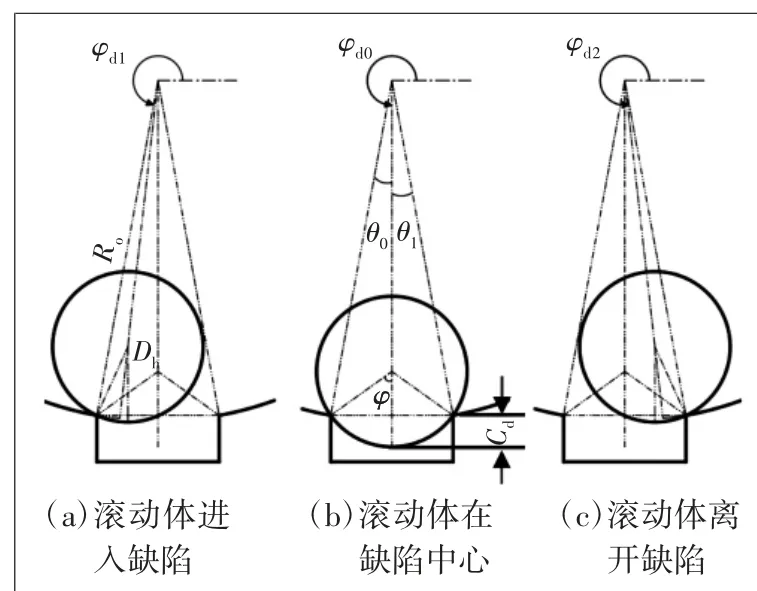
图3 外圈故障局部放大

2.2 外圈局部故障模型分析

采用龙格库塔法对式（1）进行求解，设置轴和内圈总质量mi=3.52 kg，轴内圈转速为fs=150 r/min（低速便于分析故障振动特征），外圈固定安装于基座上总质量为mo=24.05 kg，缺陷角度设置为10°。选择轴承参数如表1所示。

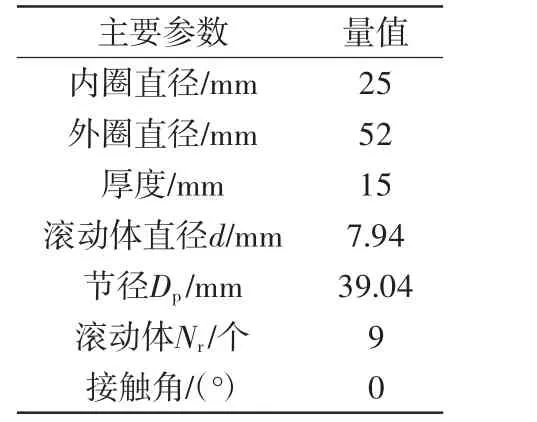
表1 仿真轴承参数表

计算生成的外圈故障振动数据如图4所示，每个衰减振动都是滚动体撞击缺陷产生的数据，图中x轴为时间轴线，可得故障周期T=0.112 s，对应的频率为f=8.928 Hz。

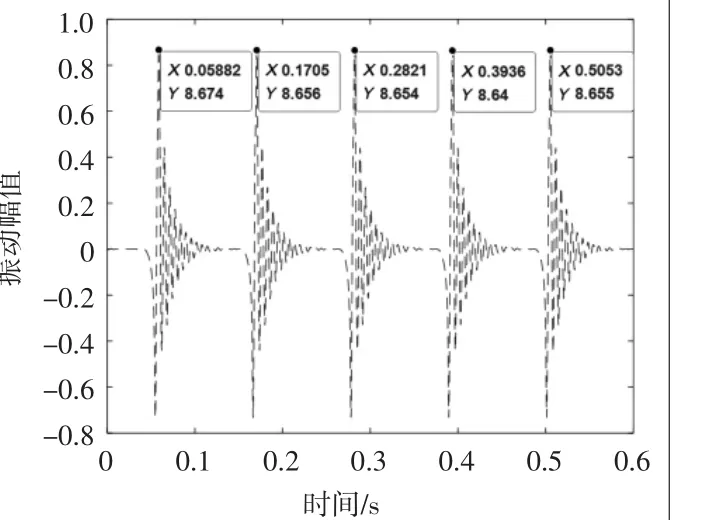
图4 滚动轴承外圈故障仿真时域图

3 轴承内圈局部故障模型创建与分析

3.1 内圈局部故障模型创建

区别于外圈安装在基座上不跟随旋转，内圈故障信号随着轴承缺陷的旋转而转动位置，其信号将更为复杂。如图5所示，随着转轴的旋转，内圈故障点也以fs进行旋转，因此故障点将分别经过载荷区和非载荷区，滚动体在载荷区故障点的振幅将大于非载荷区时的幅值。

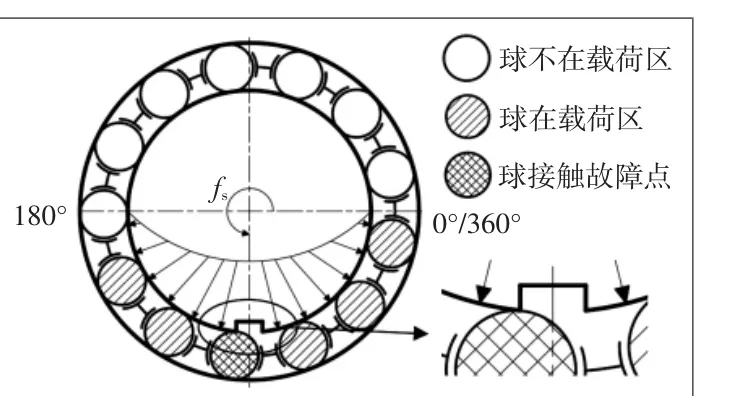
图5 内圈带故障的滚动轴承

同理，图6所示为某位置内圈故障点局部放大图，展示了滚动体由进入缺陷→到达缺陷中心位置→离开缺陷的运行过程，球进入缺陷Cd深度是随着球的位置而变化。

图6 内圈故障局部放大

内圈轨道半径为Ri，则缺陷Cd仍可用式（3）表示，其中有变化的参数为：

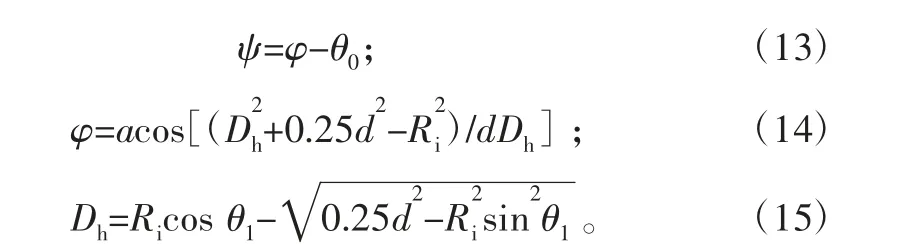
3.2 内圈局部故障模型分析

由前述理论分析可知，当假设保持架（滚动体）相对静止不动时，内圈将以相对转速ωΔ=9.45 rad/s运转。已知滚动体数Nr=9，则滚动体间隙角度为40°，因此滚动体撞击缺陷频率为13.5 Hz，即每隔TΔ=0.075 s会产生一个振动信号（如图7（a）和图7（b））。

并且通过图7（c）内圈故障包络谱可以得出基频fi为倍数的内圈特征谱线，倍频振幅随着频率增大，幅值减小，仿真结果与理论[1]描述的内圈故障特征一致，进一步验证了模型理论正确。

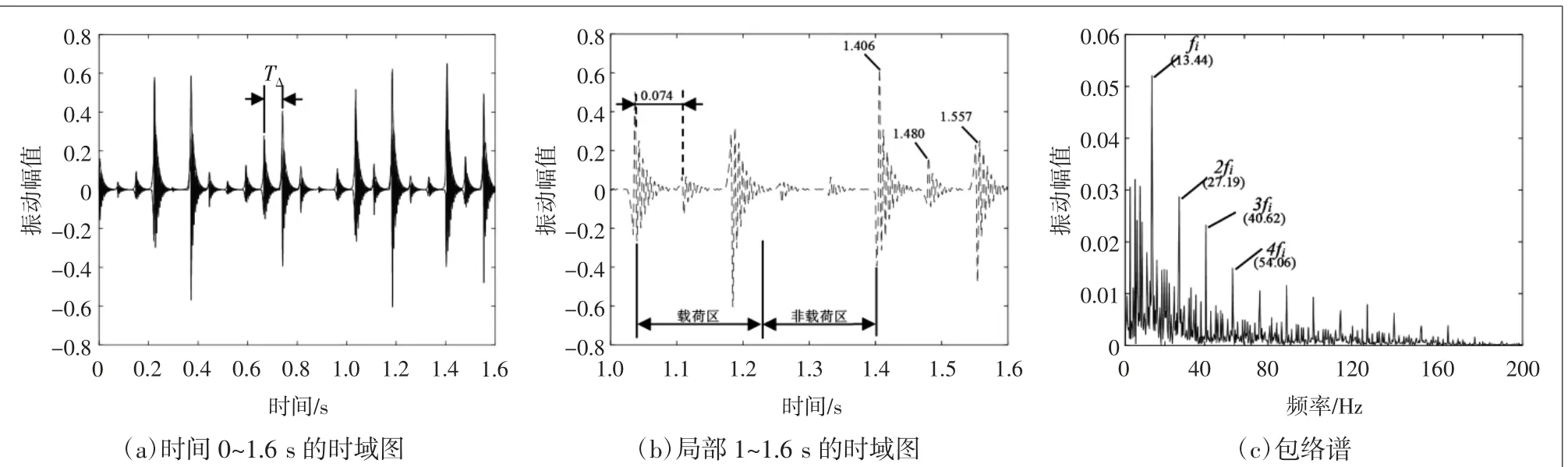
图7 滚动轴承内圈故障仿真时域和包络谱

4 轴承滚动体故障模型创建与分析

4.1 滚动体故障模型创建

滚动体故障相对于内圈与外圈故障更为复杂，因为滚动体除了随着保持架绕轴公转外，缺陷的滚动体本身也在自转，因此滚动体故障混合了内外圈故障的某些特征。如图8所示，滚动体与内圈外切并与外圈内切，设轴承坐标XOY，则φj为第j个有故障的滚动体公转角度。以O到该故障滚动体中心的射线为球体局部坐标x轴建立xoy坐标作为球的自转坐标，自转坐标xoy以保持架公转速度ωc绕XOY坐标旋转。并设滚动故障为整切面点蚀缺陷，角度θ0为故障切面中心射线与局部坐标x轴的夹角，以滚动体自转速度ωz运行。假设滚动体不发生滑移，运转方向保持不变，则理论上一个自转周期滚动体缺陷将分别碰撞内圈和外圈一次，进而产生2个幅值不同的冲击振动信号。

图8 滚动轴承滚动体故障

4.2 滚动体故障点与外圈接触

由于滚动体存在缺陷，就不可避免地在运行中滚动体球心会偏离正常球心位置Cd为

4.3 滚动体故障点与内圈接触

当滚动体缺陷边界自转到与球体局部坐标x轴180°时故障点将与内圈接触，如图9所示，将分别为缺陷进入→左边沿接触→左边线相切→达到缺陷中心点→右边线相切→右边沿接触→缺陷离开这7个步骤。

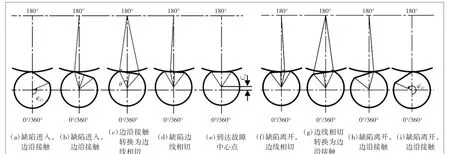
图9 滚动体故障点与内圈轨道接触

图10 滚动轴承滚动体故障仿真时域图

当边沿接触时

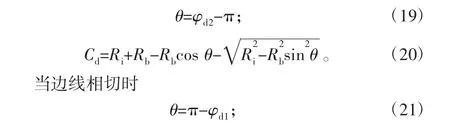
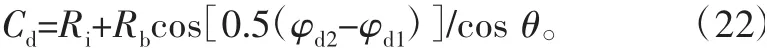
4.4 滚动体故障模型分析

滚动体每自转一圈，将分别触碰一次内圈与外圈，产生幅值不同的交替振荡信号，以转速150 r/min时保持架一个公转周期Tc内包含有12个振荡信号，图中得滚动体自转周期为Tz=0.171，即自转频率为5.882 Hz。

5 结论

本文使用六自由度轴承故障集中参数模型，分析利用故障缺陷深度变化，实现仿真故障信号的获取。通过构建一个完全正常的滚动轴承模型，然后向外圈、内圈与滚动体分别增加缺陷故障，实现故障仿真数据的生成，该方法现实可行，未来可以按照本方法扩展至多个故障及不同故障类型的故障样本数据的生成，以代替无法获取的实验数据。