基于RBF神经网络的相机标定方法

刘驰弋，谢明红，何浪

（华侨大学 机电及自动化学院，福建 厦门 361021）

0 引言

在单目机器视觉应用中，为了确定物体表面的几何位置与其图像中对应点的相互关系，需要建立相机成像的几何模型，相机标定的目的就是为了求出相机的内、外参数以及畸变系数[1]。在标定完成后，就可以对镜头的畸变进行校正，对拍摄的照片进行调整，生成校正后的图像，还原物体的形状，减小物体视觉测量的误差。作为视觉系统中的第一步，相机标定的精确与否，会直接影响视觉检测系统的误差，是整个视觉系统的关键。

传统的相机标定方法大多需要特定的标定物，或者是利用相机特定的运动信息来对相机进行标定[2-3]。被广泛使用的张正友标定法[4]，相对简单，只需要利用标定板不同位置的多张图片进行标定，但计算过程依然相对复杂。而使用神经网络对相机进行标定，可以省略求解相机内外参数的过程，直接得到畸变图像和校正图像的像素对应关系，相较于传统的相机标定方法，步骤简单，精确度高。

1 相机模型和传统标定方法

1.1 相机模型

针孔成像模型是最简单的一种相机成像模型，这种理想的线性投影模型主要由4个坐标系组成，它们之间的关系如图1所示。

图1 针孔成像模型的4个坐标系

像素坐标 系（o,u,v）：二维平面坐标系，用于描述相机CCD芯片中像素的排列位置。坐标原点O在CCD 图像平面的左上角，水平轴u和垂直轴v分别表示数字图像数据的行和列。坐标系单位为像素。

图像坐标系（O,X,Y）：二维平面坐标系，原点O位于相机光轴与图像平面的交点处，在像素坐标系中坐标为（u0，v0），X轴和Y轴分别平行于图像坐标系的u轴和v轴。坐标系的单位为mm。

世界坐标系（OW, XW, YW, ZW）：作为描述相机与被测物体在空间中的真实位置，一般将其设置在计算简便的位置处。可以通过平移与旋转得到相机坐标系。

使用齐次坐标和矩阵来表示4个坐标系之间的关系：

像素坐标系与图像坐标系几何关系：

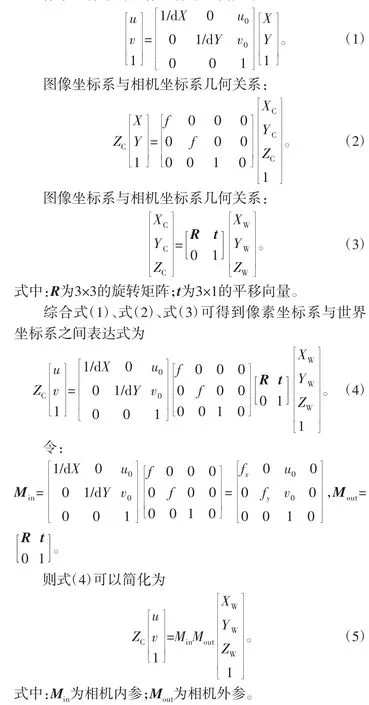
1.2 相机畸变模型

在实际中，一方面相机镜头本身形状会对成像造成影响，同时单目视觉检测系统在搭建和安装过程中也会存在一定的误差，这些都会使成像图片发生一定的畸变。根据畸变类型的不同，通常将畸变划分成径向畸变和切向畸变，如图2所示。

图2 畸变示意图

径向畸变根据偏移的方向分为枕型畸变和桶型畸变两种。径向畸变一般在图像中心畸变较小，在图像四周则畸变较大。一般使用泰勒公式来对畸变坐标进行描述：

2 RBF神经网络标定方法

传统的相机标定方法中，张正友标定法是其中被广泛使用的一种。张正友标定法在使用时借助一张二维平面模板，从多个不同角度拍摄多张（至少3张）模板照片，分别对各个图像中的特征点坐标进行提取，之后利用得到的像素坐标求解在无畸变情况下的相机内外参数并使用极大似然法提升精度。在得到无畸变相机模型，应用最小二乘法求出实际的径向畸变参数，综合内外参合畸变系数，最终再优化估计，提高精度。张正友标定法虽然所需标定板简单，只需要二维平面模板，但相机标定的好坏和输入的标定图像相关，不同的图像可能导致多次标定的结果并不一样，而且张正友标定法主要针对的是径向畸变进行校正，在一些切向畸变影响较大的场合，效果会大打折扣。而基于RBF神经网络的相机校正方法，则不需要考虑畸变的复杂情况建立复杂模型，直接对图像进行校正。

2.1 RBF神经网络

径向基函数（RBF）神经网络是一种前馈型神经网络，它起源于数值分析中的多插值的径向基函数方法，1988年Broomhead和Lowe首先将径向基函数应用于神经网络设计，从而构成了RBF网络[5]。相较于一般BP神经网络，RBF神经网络具有更好的泛函逼近能力，而且收敛速度更快，有着更好的非线性拟合能力，可以更好地应用在相机标定上。

标准的径向基函数神经网络由输入层、隐含层以及输出层3层网络组成，二输入单输出模型结构如图3所示。

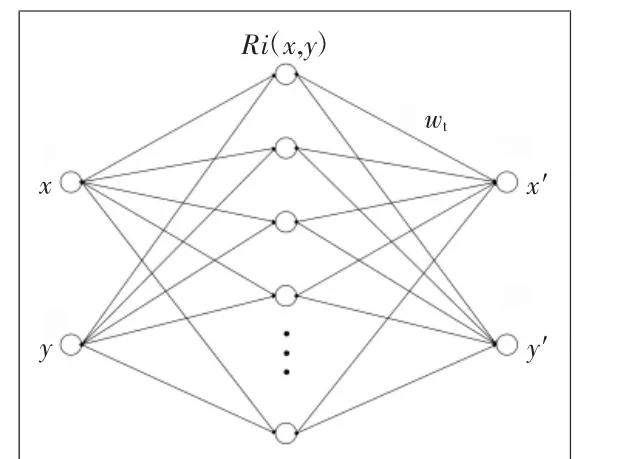
图3 RBF神经网络结构图

与BP网络的隐含层不同，RBF神经网络的隐含层作用函数是径向基函数。径向基函数是指输出仅依赖于输入与原点中心距离的函数，常用的径向基函数有高斯函数、反演S型函数、拟多二次函数等。RBF神经网络中间隐含层节点是径向基神经的核，以高斯函数为例，输入层节点只传递输入信号（x，y）到隐含层，隐含层输出表达为

2）调节隐含层节点中心和宽度。根据梯度下降法，分

2.2 基于RBF神经网络的相机标定

本文使用棋盘格标定板进行相机标定，使用棋盘格如图4所示，角点数目为11×8个，标定板黑白格子的规格为30 mm×30 mm。相机标定流程如下：

图4 棋盘格标定板

1）采集棋盘格的图像并进行预处理。将棋盘格放置于相机镜头正中间，采集棋盘格图像如图5所示，使用canny算子对图片进行滤波降噪处理，并使用灰度拉伸算法增强黑白格对比度。

图5 棋盘格标定图

2）提取角点坐标。使用OpenCV提取图像分两步提取标定图像的角点坐标：首先先使用提取角点的像素级坐标，之后使在像素级坐标进一步基础上提取角点的亚像素级坐标。使用drawChessboard－Corners()在图像中标记出所检测到的角点，检测结果如图6所示，提取到一共88个角点的亚像素坐标值，对它们进行归一化处理。3）搭建并初始化RBF神经网络。搭建一个双输入双输出的RBF神经网络，通常来说，RBF的中间隐含层节点越多（但不超过样本数），RBF的拟合效果越好，但同样会使网络计算量增大，降低网络的工作效率。综合考虑本文选用的中间隐含层节点个数为20个。使用K-means聚类算法，对采集到的角点进行计算，得到20个聚类中心将其赋值给神经网络的隐含层节点的中心值，同时根据各聚类中心之间的距离确定各隐含层节点的宽度。

图6 角点检测图

4）设置角点的训练目标。通过检测到的棋盘格角点4个顶点的角点坐标，可以将其拓扑成正四边形，根据实际中棋盘格角点的平行垂直关系，可以设定相对应的各个角点的校正目标理想坐标值。

5）训练网络。使用所检测到的88个角点坐标值以及它们对应期望值作为样本，使用梯度下降算法对RBF神经网络进行训练。得到的神经网络可以得到畸变图像像素点坐标与校正图像像素点坐标的对应关系。

6）生成校正图像。神经网络进行训练之后，遍历原图像整个像素点，将各个像素点带入网络进行计算，得到对应的校正图像的像素点坐标，对校正的像素点坐标进行判断，判断坐标是否超出图像的边界范围，如果对应坐标在校正图像中，就将原图像该点灰度值赋值给对应点的灰度值。对于超出图像边界的点坐标则进行舍弃。

7）处理遗漏的点。遍历完原图像后，校正图像中的像素坐标仍然会遗漏一部分空白的背景点并没有进行赋值处理，进行遍历找到这些遗漏的点，对这些点的八连通域进行判断，将周围的非空白像素点进行加权后赋值给遗漏点。

至此，整个相机标定完成。通过标定可以对拍摄到的图像畸变进行校正。

2.3 实验结果

使用RBF神经网络对标定图片进行校正，提取校正之后的角点坐标，与设定的期望坐标进行比较，部分数据如表1所示。

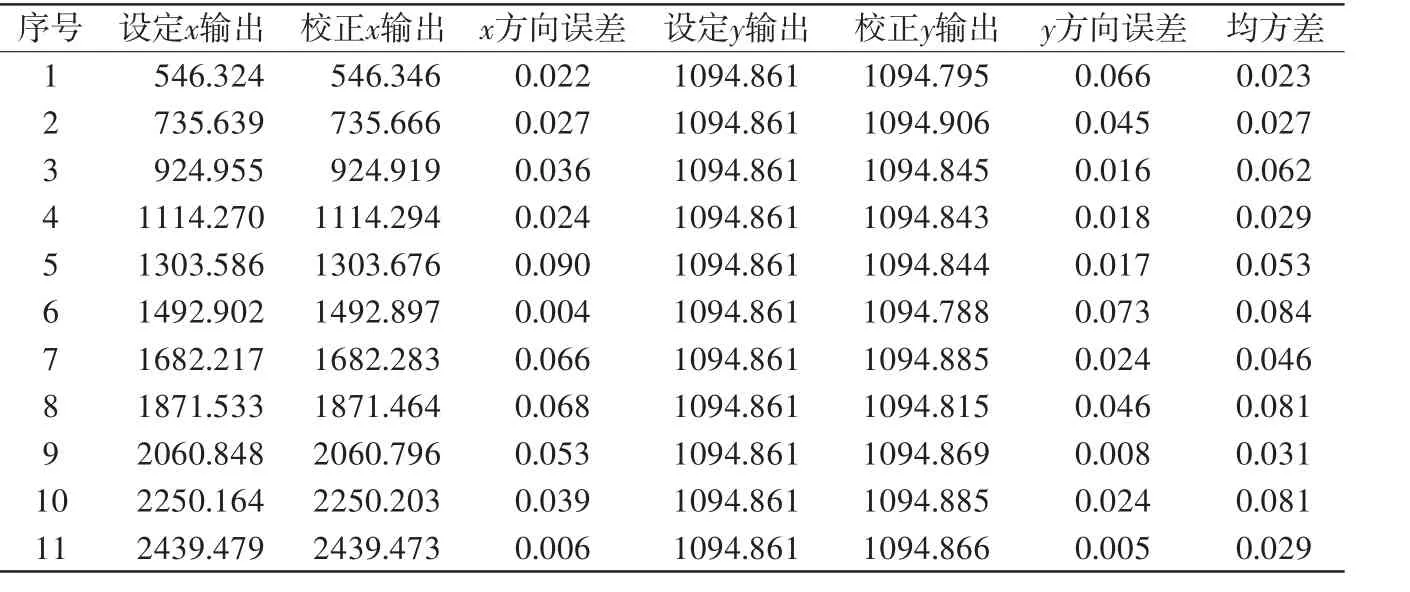
表1 角点坐标对比表（像素）

总体像素坐标误差分布如图7所示：88个角点像素总误差为4.907个像素，平均均方差为0.039个像素，其中有7个角点均方差大于0.1个像素点，x方向误差大于0.1个像素点的坐标有2个，y方向上误差大于0.1个像素的坐标有3个。图像中间的角点校正效果较好，误差较小，因为网络隐含层节点大多数位于图像中间，对边缘坐标的拟合效果较差，图像边缘的校正误差相对较大。

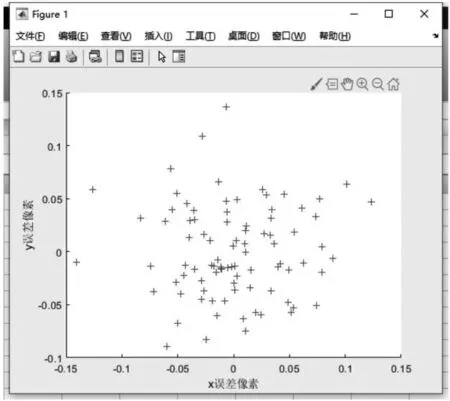
图7 重投影误差图

3 结论

本文应用RBF神经网络对棋盘格角点进行非线性拟合，经过训练的网络可以得到畸变图像与校正图像之间的像素对应关系，进而完成图像的校正工作。这种方法不需要求解传统相机标定中的复杂相机模型，过程简单，同时精准度也较高，经过实验证明，该方法可以很好地完成相机标定的工作。