基于逆有限元的机翼蒙皮变形监测方法仿真研究*
付书山, 孙广开, 何彦霖, 初大平
(1.北京信息科技大学光电测试技术及仪器教育部重点实验室,北京 100192;2.北京信息科技大学光纤传感与系统北京实验室,北京 100016)
变形监测(Shape sensing)是飞行器结构健康监测的重要内容,指利用现有传感技术实时获取航空器在飞行状态下的各种信息,借助先进的信息处理方法和力学建模方法,计算出飞行器结构的形状、大小和位置在空间域或者时间域的变化。通过对比结构参数在状态前和状态后变化量,可以分析结构的损伤程度以及损伤位置,评估当前健康状态、预测飞行器的有效寿命,以降低系统故障风险、减少结构安全维护成本[1-4]。
飞机蒙皮是包围在飞机骨架结构之外,形成飞机气动力外形的维形构件。其中机翼蒙皮与机翼骨架结构作为产生和传递气动载荷的主要部件,本身承受有较大承载力。机翼蒙皮的形状直接决定了飞行器的气动特性,是影响飞机安全性能的关键部件,加上机翼蒙皮直接与外界接触,受力情况较为复杂,所以对机翼蒙皮变形测量技术是飞机结构健康监测的技术支撑,也是飞机安全监控的重要组成部分。随着机翼尺寸逐渐增大,结构越来越复杂,对飞机的安全性和可维护性提出了更高的要求。随着对飞行器结构变形监测的深入研究,基于光纤传感的结构变形监测方法成为该领域研究的核心内容[5-7]。光纤布拉格光栅(Fiber bragg grating,FBG)传感器是以光信号为传感方式的新型传感器,与传统传感器相比,除了具有体积小、质量轻、灵敏度高、抗电磁干扰、耐腐蚀能力强等优点外,还可通过波分复用的方式串联组成传感网络[8-9],其解调系统采集频率高、性能稳定,特别适用于航空航天动态监测领域。
目前,国内外一些高校和研究机构利用光纤传感技术和曲率信息对结构变形监测展开了研究。Clements 等[10]则提出了利用FBG传感器实现精确三维定位和形状测量系统,通过布置在一个由多芯光纤构成的细小智能电缆的FBG传感器测量电缆上的各个测点的弯曲曲率和挠率,推导获得电缆上的各个点的相对位置和方位,从而重构整条智能电缆的形态;Jutte等[11]提出利用FBG传感器阵列,在机翼地面载荷试验中进行全尺度的机翼弯曲和扭曲形态实时测量研究;Glaser等[12]利用FBG测量的简易梁结构曲率数据,进行了结构形态实时重构的试验分析和研究;Sun等[13]采用光纤Bragg光栅采集了模拟机翼表面的48处应变数据,使用曲面拟合的方法对机翼的变形场进行了重构,并使用视觉测量的方法对重构结果进行评价。Yi等[14]提出一种基于曲率信息的太阳帆板的变形重构算法,通过在帆板结构中布置光纤光栅传感器,结合可视化技术,实现了结构的空间曲面拟合和动态变形重构。张合生等[15]采用了正交FBG网络获取二维正交曲率信息,提出针对空间曲面的变形重构算法,并与利用单向曲率信息的重构算法进行了比较。结果表明其在弯曲变形和扭转变形状态下均有更高的重构精度。
上述学者提出的变形重构方法都较好地满足了特定领域变形监测需求,但还存在一些不足。基于曲率信息的重构方法适用于大变形的场景中,在处理微变形的情况时,易出现重构曲率不连续导致重构的曲面不够光滑和连续,重构精度不理想。针对此问题本研究提出一种基于逆有限元法和应变信息的变形重构算法,该算法采用三节点三角形单元进行结构离散,并结合Kirchhoff板壳弯曲理论进行力学建模,理论推导了逆有限元算法的可行性,最后使用翼形蒙皮结构和方形蒙皮结构验证了变形重构算法的可行性和通用性。
1 算法原理
有限元法(Finite element method,FEM)是求解数理方程的数值计算方法,是将一个连续体的求解区域离散为有限个形状简单的单元(子区域),各单元通过有限的节点进行连接,载荷通过节点在单元之间传递。根据节点的平衡条件建立节点的载荷场方程,然后将所有节点组合进行综合求解,以获得复杂工程的近似数值解。逆有限元法(inverse finite element method,iFEM)与有限元法思想相同,其本质为利用分片插值逼近全域问题[16-17],但在某些环节的构造与计算上存在区别。首先根据待求解对象的几何特点,将其视为板、杆、梁、壳一种或多种结构的组合体,然后选择有限个一维、二维或三维单元对其进行离散。单元内任一点的位移d(x)可以由沿坐标轴方向的分位移表示,即

式中,x≡(x,y,z)表示单元上任一点的坐标;u、v、w分别为沿x轴、y轴、z轴方向的位移分量;N(x)为单元形函数;qe为单元全部节点位移组成的位移向量。
针对结构的几何特点和受力特点,选择合适的受力模型,如Kirchhoff薄板理论、Mindlin中厚板理论等来描述结构在变形状态下应变和位移的关系。结构体的应变场可以由n个独立的应变分量来描述,每个应变分量表示一个方向的应变,即ε≡{ε1,ε2,ε3, ...,εn},将应变场用单元位移向量qe和单元的插值函数来表示为

式中,x≡(x,y,z),表示应变测点的坐标;[]为求导算子,表示对单元形函数N(x) 求导;S(x)为应变-位移矩阵。
通过理论应变值ε与实测应变值εε构建的误差函数Φ,其中εε≡{},使用最小二乘法求解误差函数的极值。误差函数表达式为

式中,k为整体结构设置的应变测点数量;假设结构体离散为M个单元,每个单元设置m个应变测点,则总的误差Φ可以看作所有单元误差Φe之和:

对于每个单元,当Φe取值最小时,可以认为此时的模型最能反映出结构的变形情况。将式(2)带入式(4)可知,单元误差函数Φe是关于单元位移向量qe的函数,根据最小二乘法的求解原理,当Φe取得最小值时,此时有

求解方程会得到Keqe=Fe形式的方程,其中Ke为单元刚度方程;Fe为单元载荷向量。通过相应的坐标变换,对各个单元刚度矩阵、单元载荷向量进行组装,再添加结构体的边界限制条件,最终得到结构体的总体平衡方程为

式中,K为结构总体刚度矩阵,只与单元形函数和测点坐标有关;F为总体载荷向量,只与测点应变值有关;q为待求节点位移向量,通过计算q=K-1F即可求出节点位移。至此,通过结构表面的应变值反解出结构位移值的全部过程,通过实时读取应变值并计算q=K-1F即可得到结构体各个节点的实时位移,对于非节点处的位移,可以通过式(1)中节点位移和形函数插值得到。机翼蒙皮变形重构逆有限元算法实现流程如图1所示。

图1 机翼蒙皮变形重构逆有限元算法实现流程Fig.1 Inverse finite element algorithm for wing skin deformation reconstruction
2 试验方案
2.1 机翼蒙皮变形特点
分析机翼蒙皮的几何尺寸和受力特点,由于其厚度远小于长宽尺寸,如图2所示,可以将其看作薄板结构。机翼蒙皮承受空气动力作用后将作用力传递到相连的机身机翼骨架上,机翼蒙皮的位移为机翼的位移,作用于机翼蒙皮上的载荷分为两种类型: (1)平行于蒙皮表面的纵向载荷,属于平面应力问题; (2)垂直于蒙皮表面的横向载荷,属于薄板的弯曲问题。由于机翼的实际受力主要为垂直于机翼表面竖直方向的气动载荷,机翼蒙皮的受力变形问题可以采用Kirchhoff弯曲理论来分析,该理论满足3个假设。

图2 机翼蒙皮结构模型Fig.2 Wing skin structure model
(1)直法线假设。薄板中面法线变形后仍保持为法线且长度不变,有

(2)板厚不变假设,忽略板中面的法线应力分量,且不计其引起的应变。板内各点的挠度w与z坐标无关,只是x,y的函数,即

(3)中面不变形假设,即薄板中面内的各点没有平行于中面的位移,即

按照Kirchhoff计算假设,机翼蒙皮结构的变形弯曲问题等价于蒙皮中面的变形弯曲问题,中面上的一点实际上代表着一个长度为板厚2t法线段,t表示中面到薄板表面的距离,即中面的变形挠度就是蒙皮整体的变形挠度。对于中面上的任意一点位移都有3个位移分量w、θx、θy,分别表示挠度、法线绕x的转角和法线绕y的转角。当中面的位移为小挠度位移时,其转角位移分量θx、θy与挠度w存在如下关系:

机翼蒙皮表面的应变场ε包含3个应变分量{εx,εy,εxy},分别表示x方向的应变、y方向应变、xy面内的切向应变。根据几何方程,应变场ε可表示为
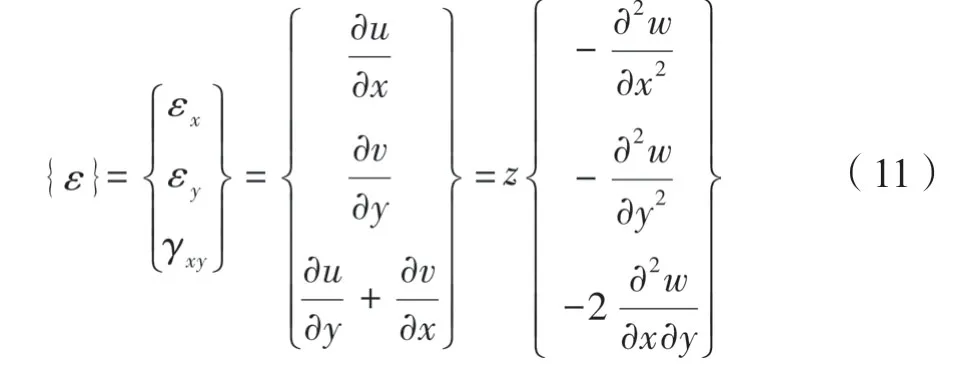
由式(11)可知,中面(z=0)内既没有面内应变,也没有面内应力,只需测量蒙皮表面(z=±t)的应变数据,根据应变位移的几何关系,可求解机翼蒙皮的变形量。
2.2 结构离散方案
逆有限元法求解蒙皮弯曲变形问题,首先需要对机翼蒙皮结构进行结构离散。常用的离散单元有三角形和矩形单元,由于三角形单元有较好的边界适应性和灵活性,工程实用价值较大。本研究选取9自由度三角形单元来对蒙皮结构进行离散,如图3所示,三角形单元节点位移向量qe可表示为

图3 9自由度三角形单元Fig.3 Nine degree of freedom triangle element
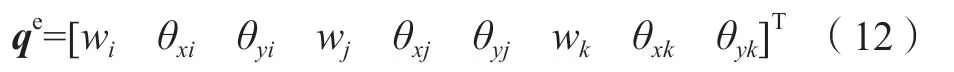
2.3 应变测点布设方案
由于蒙皮的上下表面关于中面对称,当蒙皮发生弯曲变形时,其上下表面的应变数值理论上是相等的,通过在蒙皮表面粘贴应变花,获取该测点3个方向的应变值εx、εy、γxy。单个应变花由3个FBG传感器构成,其放置方向与x轴分别成0°、45°和90°夹角,如图4所示,其中各方向FBG测量值与应变分量的对应关系为

为了使应变测点能够较为均匀地分布在蒙皮表面,对进行结构离散的每个三角形单元均设置7个应变测点,测点位置如图4所示,测点的坐标值在表1中列出。其中测点1在三角形单元的形心位置,测点2、3、4分别在形心到3个顶点的三等分处,测点5、6、7分别在线段2—3、3—4、2—4的中点。通过选取不同位置、不同数量的应变测点来探究重构精度与测点位置和数量之间的关系。

图4 单元应变测点布设位置和FBG布设方式Fig.4 Location of strain measuring points and FBG layout in unit

表1 应变测点位置坐标Table 1 Position coordinates of strain measuring points
2.4 机翼蒙皮变形有限元仿真
为验证逆有限元算法的变形重构性能,选择基于Ansys平台对机翼蒙皮结构进行有限元变形仿真。蒙皮材料选择铝合金(杨氏模量E=7.1e+4MPa,泊松比v=0.33),几何尺寸如图5(a)所示,厚度为2mm。采用1843个三角形单元对其进行离散,机翼左端固定,整体为悬臂板受力模型,并在蒙皮表面施加50N的均布载荷,方向为z轴正方向(图5(b))。机翼蒙皮变形有限元仿真云图如图5(c)~(f)所示,选取蒙皮表面的仿真应变值作为试验测量的应变值,带入iFEM形变重构算法,把重构出的位移量与有限元仿真得到的位移量进行对比,可以得到算法的重构精度。

图5 机翼蒙皮变形有限元仿真结果Fig.5 Finite element simulation results of wing skin deformation
2.5 算法重构精度评价
使用FEM的分析结果作为对照真值,对iFEM重构算法的性能进行评估。评价指标包括各个节点的重构误差ei以及各节点重构误差的均方根值(RMSE),其表达式为

式中,ei为节点重构误差的表达式;为iFEM算法重构的节点位移;为有限元仿真得到的节点位移;m为节点总个数。
3 结果与讨论
3.1 测点密度α与重构误差的关系
为探究单元内应变测点密度与重构精度的关系,分别将机翼蒙皮结构离散为4、6、8个单元,如图6(a)~(c)所示,并定义测点密度变量α,表示每个单元内设置α个应变传感器,α取值为1~7。当测点密度α=1时,该测点默认在三角形的形心处。当测点密度α>1时,则在图4所示的位置中随机选择测点。3种离散方案对应的测点密度与重构误差的关系如图6(d)~(f)所示,对于每种离散方案,机翼蒙皮变形重构误差均随单元测点密度增大而减小,随后趋于平稳。在单元测点密度α从2增至7的过程,3种离散方案的重构误差分别减少了1.08%、0.79%和0.45%,减小幅度并不明显。当单元测点密度相同时,重构误差随单元数量增加而减小,具体数据如表2所示,仿真位移对比如图7所示。另外,只在形心位置设置一个测点时(α=1),其重构误差相对更小。

图7 离散方案3、α=1工况下,iFEM算法重构位移与FEM仿真位移对比Fig.7 Comparison of displacement reconstructed by iFEM and simulated displacement of FEM in discrete scheme 3, α=1

表2 离散方案3、α=1工况下,各节点位移重构误差Table 2 Displacement reconstruction error of each node in discrete scheme 3, α=1

图6 机翼蒙皮离散方案和测点密度与重构误差的关系Fig.6 Discrete scheme of wing skin, and relationship between density of measuring point and reconstruction error
3.2 测点密度β与重构误差的关系
为进一步探究逆有限元算法的应变测点密度与重构精度之间一般性的关系,并验证该算法对蒙皮变形重构具有通用性,继续选取具有较大尺寸蒙皮结构作为研究对象。大尺寸蒙皮结构是构成并维持飞行器气动外形的重要组件,广泛应用于空间站、卫星帆板、深空探测器、大展翼飞机等航空航天器结构组成中[18],其尺寸通常在数米以上。本研究选取边长为6m×6m的方形蒙皮结构,使用Ansys平台对其进行仿真变形,固支条件为4边固定,并设置垂直蒙皮表面大小为20N的均布载荷。蒙皮使用材料和厚度与前文中翼型蒙皮相同,以保持蒙皮受力弯曲特性的一致性。定义测点密度变量β,表示每m2设置β个应变传感器,如图8所示。

图8 6种不同的应变测点密度布设方案Fig.8 Six different layout schemes of strain measuring point density
通过在蒙皮表面设置不同的测点密度,获得测点密度与重构精度的关系,如图9所示,总体重构误差随测点密度增大而减小。当测点密度β=1.39个/m2时,重构误差<2%,当测点密度β>3个/m2后,重构误差基本不再减小并趋于平稳。当测点密度β从5.56个/m2减小至2个/m2时,重构误差从最小值0.51%上升至1.2%,误差未明显增大,仿真位移如图10所示。
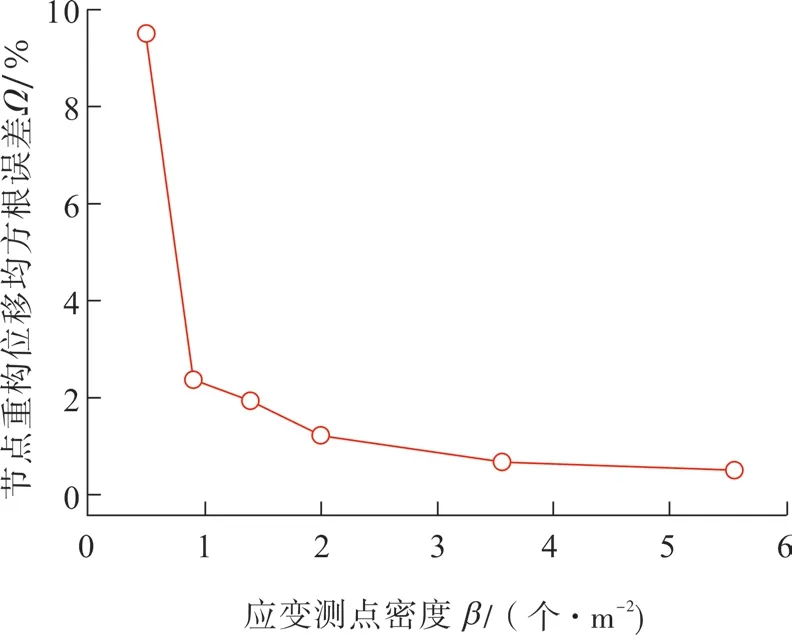
图9 蒙皮结构的测点密度与重构误差的关系Fig.9 Relationship between density of measuring points and reconstruction error of plate structure

图10 测点密度β=2个/m2工况下,iFEM算法重构位移与FEM仿真位移对比Fig.10 Comparison of displacement reconstructed by iFEM and simulated displacement of FEM in measuring point density β=2/m2
4 结论
(1)采用翼形蒙皮结构和方形蒙皮结构对逆有限元算法进行验证,试验结果表明,逆有限元变形重构算法对于蒙皮变形监测具有可行性和通用性。
(2)变形重构误差随离散单元数量和测点密度增加而减小;测点密度设置为2个/m2时,整体重构均方根误差为1.2%,最大位移处的重构误差为1.07%,重构时间<20ms;在测点密度一定时,测点位置放置在单元形心处可以获得更小的重构误差。
(3)基于应变信息的逆有限元变形重构方法可以实现机翼蒙皮变形动态监测,在飞机蒙皮结构变形监测领域具有应用前景。采用离散单元分析思想,能够适用于微小变形和复杂结构变形监测领域,应用场景广泛。

