多模态耦合的覆冰导线风致舞动分析
张会然,杨雄骏,刘中华
(厦门大学建筑与土木工程学院,福建 厦门 361005)
输电导线舞动是影响输电线路安全的重要因素,是对电网安全运行危害较大的故障类型.舞动主要是由于导线上有不均匀覆冰,从而在风力作用下产生的低频大幅度自激振动现象.关于覆冰导线舞动已经有不少研究,主要的研究方法是通过建立有限元模型[1-2]和建立覆冰导线非线性动力理论模型进行覆冰导线舞动分析.其中以索结构为基础建立覆冰导线连续体非线性动力计算模型[3-6],可以定性地讨论覆冰导线舞动的非线性运动特性.但目前基于覆冰导线非线性三维连续体动力模型的舞动分析多集中于各方向上第一阶模态的耦合.刘海英等[7]和楼文娟等[8]运用Galerkin方法进行一阶模态截断将偏微分方程转化为常微分方程,分析覆冰导线的舞动随系统参数的变化规律.输电导线是三维连续体,在发生舞动时不仅只有第一或某阶模态的振动,舞动分析时考虑多阶模态的耦合振动是有必要的,可以更清楚地分析导线发生舞动时各阶模态的振动情况.Luongo等[9]建立了只考虑面内多阶模态耦合的模型,初步分析了覆冰导线在面内多阶模态耦合的舞动.霍冰等[10]考虑了覆冰导线面内前4阶和扭转前4阶模态耦合动力模型,研究分析了在不同风速、初始拉力等条件下各阶模态的舞动,但没有考虑面外的振动.
覆冰导线的舞动是在风致作用下发生的自激振动,通常还需要考虑风场的随机性.谐波叠加法是用于脉动风时程模拟的传统方法之一,在谐波叠加法中,Cholesky分解与三角级数叠加将耗费大量的计算时间,但是对于像输电导线这样的大跨度结构,需要模拟的点数较多,因此提高模拟效率变得十分重要.Yang[11]在模拟过程中引入快速傅里叶变换(FFT),大大提高了三角级数叠加的计算效率.Ding等[12]在互谱密度矩阵的Cholesky分解中引入三次Lagrange插值,减少了Cholesky分解的次数.目前关于覆冰导线舞动在随机风场中的研究,大多是基于有限元模型,刘小会等[13]和严波等[14]通过ABAQUS软件建立有限元模型,研究了四分裂导线在随机风场中的舞动和防舞装置.楼文娟等[15-16]通过ANSYS软件建立覆冰导线的有限元模型,研究了覆冰导线在三维瞬态风场下的舞动响应和脉动气动力特性及风偏响应.考虑多模态耦合的非线性覆冰导线模型在随机风场中的舞动研究还较少.
本文在覆冰导线非线性三维连续体动力模型基础上,运用Galerkin方法进行多阶模态截断,得到面内-面外-扭转方向多模态耦合的动力分析模型,通过Lyapunov稳定性理论对覆冰导线稳定性进行判断,分析稳定风场中不同风速下覆冰导线各阶模态振动情况.并为了提高脉动风场模拟效率,采用Hermite插值改进Cholesky分解的脉动风场模拟方法,模拟输电导线所在的随机风场,进一步分析在随机风场下覆冰导线各阶模态的舞动特性.
1 考虑多模态耦合的覆冰导线模型建立
1.1 覆冰导线三维连续体模型

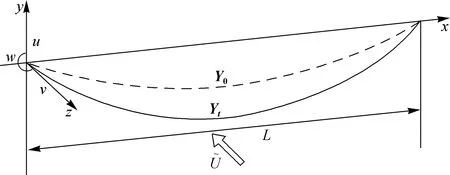
图1 覆冰导线三维模型Fig.1 The model of iced-conductor
沿导线长度方向选取微元分析,得到覆冰导线面内-面外-扭转三向耦合的偏微分动力方程[12]:
(1)

覆冰导线截面有新月形、扇形、D形等,以新月形截面为例,覆冰导线截面风攻角示意图如图2所示.基于准定常假定,作用在覆冰导线单位长度上的气动荷载表示为:

图2 覆冰导线截面(新月形为例)Fig.2 Iced-conductor section(crescent shaped)
(2)

1.2 基于Galerkin法进行多模态离散
为详细分析覆冰导线舞动时各模态之间的耦合作用,采用Galerkin法对得到的覆冰导线偏微分方程进行离散.离散后的面内、面外和扭转位移可表示为:
(3)
式中:Ui(t)、Vj(t)、Wk(t)为系统的模态坐标,φn为各阶振动模态.
以各个方向各展开2阶模态为例,即令M=N=Q=2,得到系统面内-面外-扭转3个方向耦合的二阶6自由度常微分非线性动力方程:

(4)
式中:aij、bij、cij和gIij(i=j=1,2)为几何线性项积分系数和气动荷载线性项积分系数,QIj和GIj为几何非线性项和气动荷载非线性项.为进一步进行稳定性分析,将公式(4)转化为:

(5)
2 覆冰导线在稳定风场中的舞动分析
2.1 覆冰导线舞动稳定性判断


(6)
其中A为系统线性化矩阵:
(7)
N为系统的非线性项,Apq(p=q=1,2,…,6)为状态运动方程中各状态变量的系数.

2.2 稳定风场下覆冰导线舞动响应的求解
3 覆冰导线在随机风场中的舞动分析
3.1 基于Hermite插值改进Cholesky分解的随机风场模拟
对于n维零均值平稳随机过程,将互功率谱密度矩S(ω)进行Cholesky分解可得:
S(ω)=H(ω)·H*(ω)T,
(8)
式中H*(ω)T为H(ω)的转置共轭矩阵.而随机过程uJ(t)的样本可由下式来模拟:
(9)
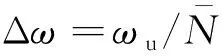

采用三阶Hermite函数近似表达H矩阵,需要计算插值点处的函数值与其一阶导数值.建立区间内的Hermite插值函数:
(10)

(11)
3.2 随机风场下覆冰导线舞动响应的求解
(12)
4 算例分析
4.1 覆冰导线特征段线路参数
本文选取单根新月型截面覆冰导线为研究对象,覆冰截面如图2所示,导线型号为XLGJ-400/50,物理参数如表1所示[8],覆冰导线初始风攻角α0为60°.得到各阶模态的固有频率如表2所示.

表1 单根新月型覆冰导线物理参数

表2 面内-面外-扭转方向各阶固有频率
4.2 稳定风场中的舞动分析
根据建立的覆冰导线多模态耦合非线性动力分析模型,得到的系统稳定特征曲线(图3),求得两个模态的临界风速4.3 m/s和7.3 m/s.进一步数值求解得到在不同的风速下,各阶模态的响应时程.

图3 系统稳定特征曲线Fig.3 System stability characteristic curve

图4 面内-面外-扭转各阶模态的振动响应时程Fig.4 Time history responses of in-plane,out-plane and torsion m/s)
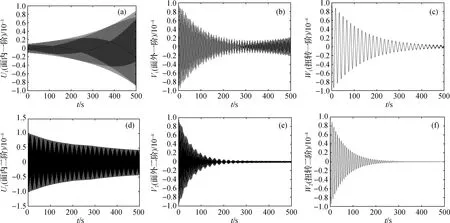
图5 面内-面外-扭转各阶模态的振动响应时程Fig.5 Time history responses of in-plane,out-plane and torsion modes m/s)

图6 面内-面外-扭转各阶模态的振动响应时程Fig.6 Time history responses of in-plane,out-plane and torsion modes m/s)
4.3 随机风场中的舞动分析

脉动风速时程曲线、模拟风场功率谱与目标功率谱如图7所示,采用本文提出方法所模拟的脉动风的功率谱密度函数和互相关函数均与目标值拟合很好.

图7 脉动风场数值模拟结果Fig.7 Numerical simulation results of fluctuating wind field
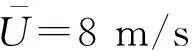

图8 随机风场中面内-面外-扭转各阶模态的舞动时程响应Fig.8 Time history responses of in-plane,out-plane and torsion modes in stochastic wind m/s)
为进一步分析脉动风对覆冰导线的舞动影响,得到面内-面外-扭转方向的位移响应频谱,如图9所示,在只考虑了平均风速的覆冰导线舞动中,面内-面外-扭转各阶模态振动以第一阶模态为主,其频率接近于面内一阶固有频率(见表2),且面内一阶模态舞动幅值最大,考虑了脉动风影响后,各阶模态振动频率发生改变,激起了面外一阶频率,扭转方向也出现了扭转一阶的频率成分,对比各阶模态的响应幅值,相比稳定风场面外一阶模态幅值中增大,舞动模式发生改变,面内-面外-扭转的耦合更加强烈.由于脉动风具有较宽的激振频率区间,能够激起覆冰导线各阶模态的振动.

图9 面内-面外-扭转的位移响应频谱Fig.9 Displacement response spectrum of in-plane,out-plane and torsion
5 结 论
本文基于覆冰导线面内-面外-扭转方向多模态耦合的非线性动力分析模型,对面内-面外-扭转各方向分别展开两阶模态进行分析.在稳定风场中,应用Lyapunov理论对覆冰导线稳定性进行判断,得到了两个临界风速,结合四阶变步长Runge-Kutta法,计算不同风速下覆冰导线各阶模态的振动响应.可以发现,随着风速的增加,某些模态的稳定性发生改变,从而引起覆冰导线的舞动,详细分析了多模态耦合下各阶模态的舞动特性.利用Hermite插值改进Cholesky分解的脉动风场模拟方法,提高了模拟的计算效率,模拟得到脉动风速时程.进一步计算了随机风场下覆冰导线的振动响应,并与稳定风场中的振动进行对比,通过位移时程响应和位移频谱分析了脉动风对覆冰导线各阶模态振动的影响.结果表明,由于脉动风具有较宽的激振频率区间,能够激起覆冰导线稳定风场中没有发生舞动的面外和扭转方向的低阶模态.

