基于交互式多模型滤波算法机车车速估计

邓雯琪， 黄景春， 康 灿, 李 强

(西南交通大学 电气工程学院，四川 成都 611756)

0 引 言

在机车粘着控制系统中，精确的车速是关键的状态参数，该值很大程度会影响控制效果，所以精确的机车速度估计尤为重要。一般情况下，在重载机车平稳运行过程中，一般取最小轮速作为机车的车速。但是车轮在机车运行中会受到外界因素的影响，例如轨面状况会直接影响车轮的运行情况，严重时可能引起车轮急剧空转，这时，轮速和车速呈现出严重的非线性关系，此时不能用轮速作为车速。因此，很多研究者对于机车车速提出了很多间接估计车速的方法，其中对于状态估计来说，以卡尔曼滤波为基础进行的车速估计很多。文献[1]提出了扩展卡尔曼滤波(extended Kalman filtering,EKF)对车速进行了估计，减少了加速度误差和部分参数拟合误差对估计结果的影响。文献[2]利用自适应卡尔曼滤波器对车辆横向和纵向车速进行了估计，文献[3]用未知输入的卡尔曼滤波估计刹车时的车速，该方法不需要加速度测量器估计瞬间的车轮加速度及刹车转矩。文献[4]利用非线性自适应滤波器对车速进行了估计，通过扩展状态维数，考虑路面附着情况和车辆响应之间的关系。上述提到的文献都能对车速进行良好的估计，但是考虑的都是单一运行轨面，没有考虑机车进行轨面变化时，粘着系数突变，车轮会产生不同程度空转。实际机车运行过程中，运行轨面是未知的，不同轨面下的粘着系数不同，机车获得的粘着力不同，所对应机车运行状态不同。基于此，有学者提出了交互式多模型(interactive multi-model,IMM)算法，适应运行状态的变化，提高系统对外部环境变化的适应性，进而提高估计精度。文献[5]提出了基于IMM的不敏卡尔曼概率假设密度滤波算法，引入了状态模型软判决机制，实现对目标机动过程模式不确定处理。文献[6]提出了两阶段卡尔曼滤波自适应IMM算法，通过减少滤波器的数量，避免模型过多产生的计算复杂度且保持精度不变。交互式滤波器里面的马尔可夫矩阵保证了模型最佳匹配，文献[7]提出了马尔可夫参数自适应IMM算法，通过误差压缩比自适应调整马尔可夫概率转移矩阵，降低因为固定马尔可夫概率产生的误差。

本文提出了改进IMM滤波方法，当机车运行轨面变化时，不需要对轨面进行判断就能快速精确地实现车速的估计。

1 机车牵引动力学模型

轮轨间的粘着力是机车运行的关键，也决定了机车运行速度及牵引效率。如图1所示，与粘着力直接相关的是粘着系数，而粘着系数与蠕滑速度相关，蠕滑速度取决于轮速与车速。在轮轴上一般有轮速传感器，通过轮对转速与车速的状态方程，以及轮对转速的量测方程能够对机车运行速度进行估计。

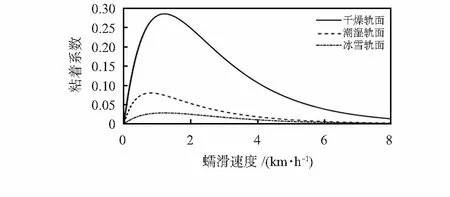
图1 粘着特性曲线

机车牵引及轮轨系统非线性程度很高，所以对实际系统需要进行简化分析。如图2所示。

图2 机车牵引力传递模型

(1)

vs=ωd×r-vt

(2)

Fa=μ(vs)×W×g

(3)

式中μ(vs)为轮轨间的粘着系数，Fa为粘着力，W为等效轴重，g为重力加速度。vs为蠕滑速度，ωd为轮角速度，r为轮径。

根据牵引动力学可以得到以下离散机车状态方程及量测方程

(4)

(5)

z(k+1)=ωd(k+1)

(6)

式中B为转动摩擦力矩系数，Rg为齿轮箱传动，a,b,c为空气阻力系数。Tm和Jm为电机输出轴间力矩与转动惯量，dTime和J为采样间隔及其转动惯量，M为机车质量。

式(4)～式(6)可以简化写成下式

(7)

式中wk与vk为互不相关的白噪声。

2 基于IMM滤波算法

IMM算法根据马尔可夫转移矩阵，融合所有子模型滤波输出值，最终使得输出结果跟踪误差最小。IMM算法包括4个步骤：输入交互，预测滤波，概率更新，数据融合[8]。考虑机车运行过程中轨面情况未知，本文考虑三种机车运行轨面设计三个子模型，分别是干燥轨面、潮湿轨面以及有雪轨面。根据如下经验公式

μ(vs)=c×e-a×vs-d×e-b×vs

(8)

其中，参数a,b,c,d的大小根据机车运行轨面选取，若轨面为干燥情况下,a=0.54,b=1.2,c=1.0,d=1.0;若轨面为潮湿情况下，a=0.54,b=2.4,c=1.6,d=1.6;若轨面为有雪情况下,a=0.54,b=1.2,c=0.1,d=0.1。如图3所示模型一、模型二、模型三。定义M={m1,m2,m3}，其中，M为子模型集合，k时刻模型出现的条件概率为μi,k，k时刻过渡到k+1时刻，模型mi转移到mj的转移概率为pij。

图3 IMM滤波模型

IMM滤波算法：

1)输入交互

(9)

(10)

(11)

式中ui/j,k为模型mi与mj的混合概率，uj,k+1|k为模型mj的预测概率,oj,k|k为第j个子模型k时刻的输入值，Poj,k|k为第j个子模型k时刻协方差,i,k-1|k-1为第i个子模型k-1时刻的估计值。

2)滤波预测

粘着系统是非线性系统，尤其在机车车轮发生空转时，轮速与车速呈现高度非线性关系。本文采用4种常见的非线性滤波器进行滤波预测，分别是EKF、二阶EKF、容积卡尔曼滤波(cubature Kalman filtering,CKF)、无迹卡尔曼滤波(unscented Kalman filtering,UKF)。

3)模型概率更新

模型似然

[Zj,k+1-h(j,k+1|k)]×(-12)}/2π|Sj,k|

(12)

模型更新概率

(13)

4)输出融合

(14)

3 改进马尔可夫矩阵

IMM滤波算法中，马尔可夫矩阵代表各子模型之间的转移概率，也决定各个子模型的输出结果所占比例，同时也作用于下一次的滤波输入环节中。传统IMM算法根据先验信息设定的马尔可夫矩阵是固定不变的，但在运行轨面未知情况下机车运行状况也未知，因此,修正马尔可夫矩阵使其自适应机车机动状况很有必要。本文采用文献[9]提出的马尔可夫矩阵修正方法。该方法通过各子模型相邻时刻概率变化表示该模型与真实模型之间的差别。因为模型转移概率不能为负数，因此可以用以下式表示

ai,k=exp(ui,k-ui,k-1),i=1,2,…,M

(15)

1)当ui,k-ui,k-1>0,则有ai,k>1；

2)当ui,k-ui,k-1<0,则有ai,k<1。

其中，ai,k代表前后两时刻第i个子模型条件概率变化情况。若该子模型随着时间逐渐增大，则说明应该增大其他模型对其转移概率，使得增大该子模型与真实模型匹配度。若该子模型随着时间逐渐减小，说明应该减少其他模型对其转移概率，使得降低该子模型与真实模型匹配度，以此实现最佳模型匹配。将ai,k作为修正系数代入转移概率，对马尔可夫矩阵里的每个转移率进行修正，如下

p′j,i=ai,kpj,i

(16)

因为马尔可夫矩阵每行概率之和为1，故需要对上式进行归一化

(17)

其中，i=1,2,…,M,j=1,2,…,M。从修正后的马尔可夫矩阵可以看出，该算法根据后验信息，即每个子模型的条件概率变化情况，自适应地修正了马尔可夫矩阵，使匹配概率大的子模型输出结果占比大。

4 试验与分析

机车牵引参数设置,如表1。

表1 机车参数设置

在仿真实验中，采样周期T=0.01 s，设置运行时间为60 s。为了验证对轨面的自适应性，假设机车从20 s干燥轨面过渡到潮湿40 s再过渡到冰雪轨面。实验仿真结果通过EKF、二阶EKF、UKF及CKF这四种常见的滤波器做对比。为了避免数据偶然性，并且加强其可靠性，蒙特卡洛仿真了150次。

不同轨面下粘着系数大小不同，若此时施加给车轮转矩过大，很可能发生空转。如图4所示，机车在20 s左右从干燥轨面过渡到潮湿轨面，以及机车在40 s左右从潮湿轨面过渡到冰雪轨面时，轮速突然增加又下降，说明此时粘着系数较前一时刻猛然下降，轮子发生了一定程度空转。

图4 不同轨面下轮速估计

如图4所示，IMM滤波算法因为其考虑多种轨面情况，在车轮处于空转与非空转情况下，都能够精确快速地跟踪运行在不同轨面下的轮速。四种不同滤波器车速估计情况如图5所示。

从图5(a)中可以看出，当机车轮子处于非空转时，机车运行前40 s时，滤波误差均在0.01 m/s左右。当机车从潮湿轨面过渡到冰雪轨面时，因为此时冰雪轨面粘着系数过低，跟踪误差增加至0.03 m/s左右。基于单个滤波器以及改进IMM滤波器的估计误差接近，跟踪精度很高。但是当机车处于空转的情况下，即机车轨面发生变化导致粘着系数骤降时，基于单个滤波器的滤波算法出现了很大的误差，而改进式IMM滤波算法能够很好适应轨面的变化且估计精度很高。

图5 四种不同滤波器下的车速估计误差

为了验证马尔可夫修正前后的效果，如表2所示，基于马尔可夫矩阵改进前后四种滤波器跟踪误差对比结果。

从表2中可以看出，IMM-EKF 跟踪效果最差，交互式多模型二阶EKF(IMM-EKFII)、IMM-UKF、IMM-CKF跟踪效果明显好于IMM-EKF。从比较结果中可以看出，IMM-EKF及改进IMM-EKF算法跟踪效果最差。二阶EKF对非线性方程展开到了泰勒展开式的第二项，更加接近非线性系统，精确性高于一阶EKF。UKF与CKF均是通过sigma采样点对非线性系统的统计特性进行近似，针对粘着系统这种高度非线性系统来说，估计效果会比近似非线性方程更好。算法的改进提高了10 %～30 %估计精度，不论马尔科夫矩阵改进前还是改进后，IMM-EKF估计误差最大，而容积卡尔曼IMM-CKF的估计效果最好。

表2 均方根误差对比

5 结 论

本文通过应用改进IMM滤波算法对机车运行车速进行了估计。通过仿真可以得出以下结论：

1)IMM滤波算法能实现在无需轨面判断情况下实现不同轨面状态下机车车速的准确估计。在车轮处于非空转与一定程度空转时也能很好跟踪机车车速。

2)改进交互式滤波算法一定程度上比传统交互式滤波算法提高一定估计精度。通过比较几种常见的IMM滤波器算法，因为机车粘着系统非线性程度高，基于Sigma采样的CKF估计效果更佳。

3)当车轮发生严重空转时，此时粘着系数降为0左右，基于单轴的滤波器估计方法已失去跟踪精度，因此,下一步打算针对严重空转单轴估计精度下降的问题，提出多轴机车车速估计方法