模糊PID控制的光束指向稳定系统*

任文佳， 刘 瑾， 杨海马

(1.上海工程技术大学 电子电气工程学院，上海 201600；2.上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引 言

激光束指向稳定控制技术在精密跟踪、无线通信、自适应光学等领域有着广泛的应用[1]。由于目标通常处于运动状态，激光光源经常受到振动，发生光束指向波动现象，这种现象是由热膨胀和支撑结构的收缩、光在大气中的传播受到湍流的影响、光学平台的振动引起出射激光不稳定而造成测量误差[2]。为解决出射光束抖动问题，提高跟踪系统瞄准精度[3,4]，因此需要建立光束指向稳定控制系统。在光束由于抖动发生偏移时，位置敏感探测器(position sensitive detector,PSD)上探测得到光束偏移量，将位置偏差反馈至控制器，然后驱动快速反射镜(fast steering mirror,FSM)转动，出射光线趋于稳定状态，使得抖动引起的误差得到了补偿[5,6]。基于单个FSM的光束指向系统存在不足[7]，因此建立基于双FSM的光束稳定系统，修正出射光束的偏差。外部干扰会使负载发生变化，影响音圈电机驱动反射镜系统的控制性能，从而使系统产生非线性变化[8]。由于经典比例—积分—微分(proportion integration differentiation,PID)控制器的参数固定，不能满足高精度、动态化的控制要求，本文将模糊控制和PID控制结合起来，对PID参数进行在线自动调节，应用于FSM音圈电机驱动反射镜系统，具有动态响应快，控制精度高的优点[9]。通过MATLAB/Simulink仿真实验对模糊自适应PID控制和经典PID仿真结果进行对比，采用模糊自适应PID控制方法可以提高FSM系统跟踪精度。

1 激光束指向稳定控制系统研究

1.1 基于单个FSM的光束指向稳定原理

光束指向稳定控制系统主要包括FSM、PSD、分光镜(beam splitter,BS)和激光器(laser)[10]。光束指向稳定原理如图1所示。

图1 基于单个FSM光束指向稳定原理

FSM和BS与水平面呈135°和45°，激光发生上下(左右)平移时，如图1虚线所示，可以看到出射光束也发生了相对应的平动。激光束经FSM反射到分光镜，一部分发生透射，一部分反射，透射出去的光束打到PSD上，光斑自原点运动到P(x,y)处。 PSD光敏面尺寸为l×l，4个电极输出的光电流为I1，I2，I3，I4，以光敏面坐标中心为原点，通过式(1)可得到光斑的位置坐标[11]。为校正这一偏转误差，需要控制器驱动FSM转动一定角度，使得出射光线恢复稳定状态

(1)

设激光器移动距离和光斑位移均为s，根据FSM转向角原理可知，校正后的入射光线与竖直轴的夹角是FSM偏转角度的2倍，激光在FSM的入射点与竖直轴的距离为X，则夹角2α和β有如下关系式

(2)

可得FSM偏转角度

(3)

考虑到偏转角α<1.5°，则式(3)已知L和s，可以得到FSM的偏转量。可以看出,此时的出射光束指向不再水平，而是与水平面呈一定角度，背离了出射光束指向稳定的要求。

1.2 建立双FSM光束指向稳定模型

通过Zemax仿真，建立双FSM光束指向稳定模型，以分析PSD光敏面光斑的变化情况。如图2所示，仿真初始条件：以平面反射镜代替FSM1与水平面呈45°置于底部，选择光束直径为1 mm、波长为486 nm的激光距离反射镜300 mm准直入射；分光镜厚度为7.5 mm，材质为BK7，分光镜距补偿镜(compensate mirror,CP)150 mm，且补偿镜的折射率和厚度均与分光镜相同；分光镜1到FSM1的距离与补偿镜1到FSM2的距离相等为300 mm；FSM1到PSD1的距离为465 mm，FSM2和PSD1关于分光镜1对称，且分光镜1,2与补偿镜1,2关于FSM2对称；目标靶面和PSD2关于分光镜2对称。

图2 双FSM光束指向稳定模型

当入射光束发生一维偏转时，假设入射光束沿水平方向的偏转角度分别为-0.2°,-0.15°,-0.1°,0°,0.1°,0.15°,0.2°时，靶面上光斑移动轨迹如图3，已知探测器PSD光敏面为10×10 mm，随着入射光束角度的变化，光斑自左向右移动，入射光束偏转角度范围是：-0.27°≤α≤0.27°，若入射光束超过上述偏转范围，则PSD光敏面上探测不到光斑。设坐标中心为原点，则光斑坐标和对准误差如表1所示。对准误差是根据探测器光斑位移计算得到的入射光束偏转角度与光束在对准目标方向上角度的差值，由于光斑位移量s相对于入射光束到靶面的距离L很小，在实际计算中将arctan(s/L)≈s/L，所以产生一定算法误差。

图3 光迹图

表1 光斑坐标和对准误差

系统中FSM的转动范围为±1.5°(±26.2 mrad)，镜面直径25.4 mm；PSD的有效光敏面为10 mm×10 mm，一般在其80 %范围内线性度较好，故取8×8 mm，则光束在PSD光敏面上平移范围是：-4 mm≤d≤4 mm。如图4所示，入射激光距离FSM1中心为L，FSM1距FSM2为D，激光偏转角度为θ，相对平移量为d1，PSD1探测光斑位移量为d，经校正后FSM1偏转α，校正后的反射光束打在FSM2中心处，光束与中轴线夹角为β，经BS2反射到PSD2上的光斑偏离光敏面的中心位置，位移为s。PSD2将光斑位置偏差反馈到控制器，调整FSM2的旋转角度γ，反射光束偏转β使光斑重新回到PSD2的中心处，最后输出的光束沿水平方向出射到达靶面。图4中PSD2和靶面关于BS2对称，可知靶面上AB之间的距离也是s，根据图4中几何关系，可以得到等式

(4)

已知L=300 mm，D=765 mm，可得FSM1和FSM2的偏转范围

(5)

入射光束偏转与平移范围

(6)

对于该系统来说，当激光源抖动超过上述范围时，由于PSD的非线性因素，探测的光斑与理论值有偏差，导致系统光束指向不稳定。

图4 基于双FSM激光束稳定系统

比较单个FSM系统和双FSM系统出射光束的理论对准误差，如表2所示，当入射激光仅绕FSM1中心转动时、仅发生平移时、既有转动又有平移时，可以看出双FSM系统的理论对准误差值为0，而单个FSM系统仅在入射光束转动时可以使出射光束指向稳定，一旦入射光束存在平移时，其出射光束不再水平。由此可知双FSM系统可以使出射光束达到指向稳定。

表2 单、双FSM系统理论光束指向误差范围 mrad

2 模糊自适应PID控制器设计

2.1 模糊自适应PID控制

模糊PID控制器为二输入—三输出系统，即输入为偏差e(t)和偏差变化率ec(t)，输出为修正量ΔKp,ΔKi,ΔKd，通过式(7)对PID控制器的三个参数Kp,Ki,Kd进行在线调整，对PID控制器进行非线性处理，适用于参数变化范围大的被控对象，使其具有良好的动态性能和静态性能[12]

(7)

K(n)由前一时刻的值和修正量ΔK决定，α,β,γ为修正量系数，设定增量对最终参数值的影响。

伺服系统模糊控制器的输入变量为反射镜角度偏差e和角度偏差变化率ec，模糊化后根据模糊控制规则(min-max-min-max)推理出ΔKp,ΔKi,ΔKd对应的模糊子集{NB,NM,NS,ZE,PS,PM,PB}，再采用重心法计算各输出量的量化值。隶属度函数用来定义输入、输出量在模糊子集的隶属度，其中,ΔKp在论域上的输出曲面如图5所示，ΔKp的模糊控制规则表如表3所示。

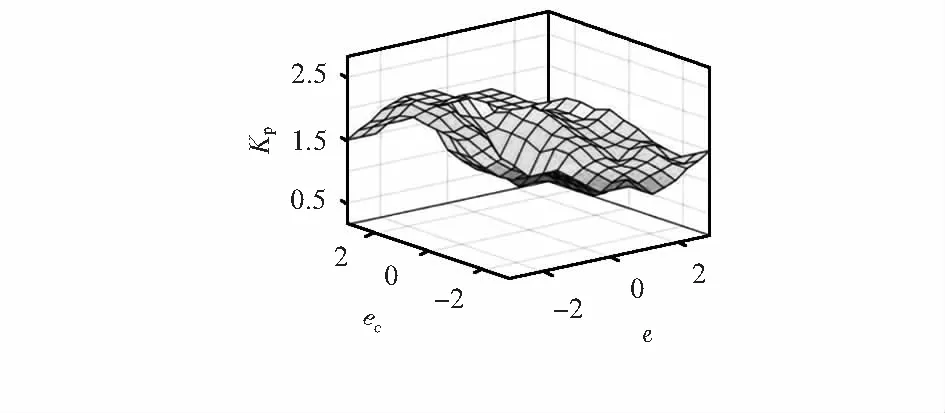
图5 ΔKp在其论域上的输出曲面

表3 ΔKp的模糊控制规则

2.2 仿真实验

根据FSM音圈电机相关参数值，得到反射镜的输入电压和输出角度的传递函数为

(8)

建立模糊自适应PID控制器和经典PID控制器系统Simulink仿真模型如图6所示。

图6 控制器仿真模型

期望FSM输出偏转角度为α′=α-e，角度误差e由PSD光敏面上的光斑位移测得。假设FSM的初始位置校准后，初始扰动信号为阶跃响应α=1°，模糊自适应PID控制和经典PID控制下的运行结果如图7所示。

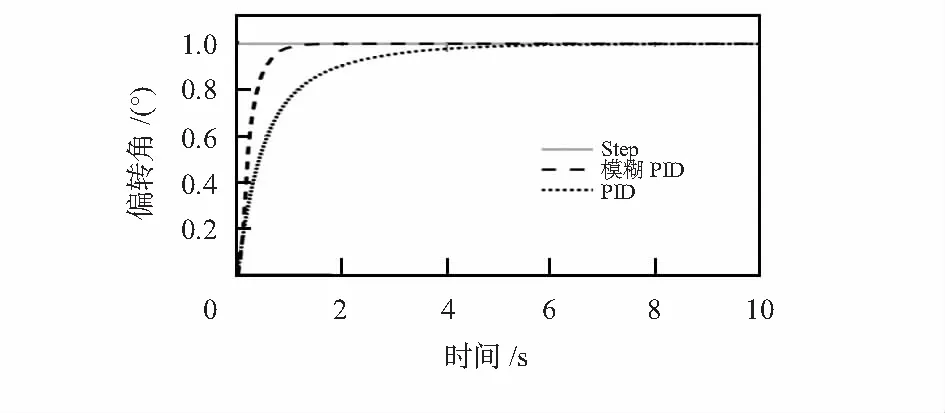
图7 模糊自适应PID控制和经典PID控制阶跃响应

仿真时间10 s，自适应模糊PID控制下的响应曲线上升速度快，上升时间为tr=266.652 ms，调整时间约为ts=878.2 ms，经典PID控制的响应曲线上升时间为tr=1.791 s，相比较之下，模糊PID系统的响应曲线达到稳定运行状态的过渡时间很短，具有良好的鲁棒性能。

初始扰动信号为阶跃响应α=0.5°，在t=5 s时加入α=0.5°的突加阶跃，FSM要跟踪目标做阶跃运动，仿真结果和跟踪角度误差如图8、图9所示。可以看到FSM系统在自适应模糊PID控制下收敛迅速，角度误差小。当加入正弦信号α(t)=sin 2t+0.5的扰动时，如图10所示，FSM跟随目标做相同运动，基于自适应模糊PID控制的FSM跟踪误差小，对准速度快，稳定性高，相比经典PID控制具有更好的跟踪能力。

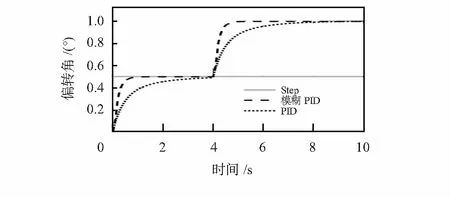
图8 FSM阶跃响应曲线

图9 跟踪角度误差对比

图10 快速反射镜正弦响应曲线

3 结 论

本文基于FSM激光束稳定原理，分析了入射光束发生偏转和平移下PSD探测光斑位移量和FSM偏转角度的数学关系。针对单个FSM光路系统的不足，构建了双FSM激光束稳定系统，给出了入射光束抖动范围，可以实现对运动目标的稳定瞄准。利用模糊自适应PID控制方法对参数进行调节，通过对比分析，自适应模糊PID控制器可以满足对受不同扰动的目标具有良好的跟踪能力。