基于简易非本征法—珀腔的大量程纳米位移传感器
孙志强, 邵志强,2, 毕佳宇, 宫占江, 王劲松, 王 烨
(1.中国电子科技集团公司第四十九研究所,黑龙江 哈尔滨 150028;2.哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150006)
0 引 言
高精度的位置测量系统和位移控制系统对于复杂的三维精密零件的绘制测量尤为重要,这些精密零件广泛应用于航空、航天、武器制造、汽车、发动机等制造领域[1~3]。微/纳米坐标测量机(micro/nano CMMs)由于能够实现纳米级的三维形貌测量,近年来已被应用于微纳精密工程进行各种复杂机械零件的测绘[4~7]。CMMs通常设计为三个正交测量轴,每个轴的末端配备一个位置测量扫描探针,并通过测量目标表面和探针之间的距离来实现三维形貌的绘制[2,3]。
测量范围大、精度高、响应快的位置扫描探头可以使CMMs系统更准确、高效地测量和描绘物体表面轮廓。许多接触式位置扫描探头已经在发表的文献中进行了大量的研究和报道。Zhang L等人[1]提出了一种微型迈克尔逊干涉仪,在光纤末端焊接一个红宝石球作为扫描探针。传感系统的测量范围可在60 μm以内,分辨率为5 nm。Zou L等人[4]提出了一种光纤悬臂梁末端熔接微型球结构作为扫描探针。该传感系统的测量范围为25 μm,分辨率为5 nm。
Li等人[5]报道了一种迈克尔逊干涉仪和钨针结合的结构作为扫描探针。传感系统的测量范围为40 μm,分辨率为30 nm。然而,非接触式三维形貌测量的研究却鲜有报道。这种测量方法的优点一方面是避免了在测量过程中降低扫描探头的长期稳定性,另一方面是防止划伤被测物体的表面。
光学非本征法布里—珀罗干涉仪(EFPI)位移传感器具有一些独特的优点,包括易于制造、体积小、分辨率高、非接触式的绝对位移测量[6,8~10]。光纤端面和反射器可以形成简单的EFPI结构[11]。光纤端面和外部反射镜之间的距离,即腔长,可以根据EFPI的反射光谱确定。根据反射光谱计算腔长,是决定整个传感系统性能的关键因素。基于宽带光源或可调谐激光器的白光干涉法(WLI)可以实现亚纳米级的绝对腔长测量[12]。因此,EFPI结构适合用于高精度一维位移传感,非常有希望作为CMMs的扫描探针,用于大范围、高精度和快速扫描响应的多维形貌测量。
本文提出并分析了一种基于白光低相干干涉为原理,非接触光学反射式的EFPI一维位移传感器。采用可调谐激光器和光电探测器(PD)作为光源和光谱接收器,用带陶瓷套管封装的光纤末端作为位移探针,互相关函数(CCF)算法作为干涉信号的解调方法。位移测量实验表面EFPI传感器的测量范围为64.52~970.55 μm,分辨率为1 nm。
1 基础理论
图1(a)展示了EFPI结构的示意图。光纤的超物理接触(UPC)型端面和平行目标表面形成EFPI结构。入射光通过光纤端面后,产生两束反射光。由于光纤的纤芯端面会产生光学反射,从光纤中出射的光,一部分打到光纤端面并产生反射光I1。其余的光作为通过光纤端面发射到空气中,并在空气中传播L0距离后,被目标表面反射,最后被光纤芯捕获的光为I2。
这两束反射光由于产生了稳定的光程差(OPD),使得光纤中产生了符合特定腔长特征的干涉光谱。其中满足干涉条件的相位φi可以表示为
(1)
式中L0为法布里—珀罗(F-P)腔的长度,λi为第i个波长的值,n为空气的有效折射率。
干涉信号(I)可以表示为
(2)
图1(b)展示的是EFPI在腔长为274.48 μm时产生的干涉光谱图,从图中可以看出中心波长为1 550 nm,带宽为40 nm的宽带光在EFPI结构中产生了干涉。峰峰之间的宽度也保持一致,这就表明这种高反射镜与光纤端面构造的F-P腔是典型的双光束干涉结构。

图1 非本征F-P腔的白光干涉理论
为了获得高精度相位信息,解算纳米级精度腔长,本文提出了一种CCF算法[13]。CCF的表达式为
(3)
式中C为F-P腔长的真实值和拟合值之间相似系数,γ为干涉条纹的对比度,L0和L分别为F-P腔长的真实值和拟合值。ν1和ν2为光源的下限和上限频率。当L与L0相同时,C(L)得到最大值,可以得到唯一且确定的腔长。
2 实验装置
整个实验装置建立在隔振光学平台上,在相对湿度为30 %RH、温度为25 ℃的条件下进行,以避免温度对空气介质折射率以及某些光学器件的热膨胀产生测量误差。
图2为EFPI微位移传感系统的示意图。该实验设置了近1 mm的位移变化范围。传感系统包括中心波长为1 550 nm、带宽为40 nm的可调谐激光器、光学环行器、带光纤陶瓷插芯封装的光纤端面、反射率为99 %镀金反射镜,光电探测器(PD)和计算机。陶瓷插芯可以帮助光纤端面提供支撑和保护,防止测量过程中外力损坏位移探头。商用单模光纤(SMF)被用作传感系统中非空间光的传输介质。

图2 EFPI微位移传感系统示意
可调谐激光器以20 pm的步长输出一系列从1 530~1 570 nm的光波,形成近似的宽带光。可调谐激光器发出的光,然后从光环行器的端口1入射到端口2,并耦合到F-P腔中。光纤芯接收两束反射光I1和I2,产生干涉,并携带腔长信息。两束反射光相互干涉,这光学反射式结构形成的干涉被称为EFPI。干扰信号经PD接收后转换为数字信号,用CCF算法解调,在计算机上获得F-P的腔长尺寸信息。
3 数据分析
反射镜的一维移动模式被用于模拟扫描探针在不同位置测量的目标物体的轮廓。图3为F-P的腔长尺寸解调数据和反射镜位移量之间的关系。采用高精度的单轴光学位移平台拖动镀金反射镜,从而改变F-P腔的长度,用于模拟位移探针遇到不同高度表面的情况。单轴手动位移平台(Newport,M-461-X-M)的精度为10 μm。整个位移变化长度约1 mm,步长为0.25 mm。随着位移长度的逐渐增加,互相关解调峰的峰值向长腔方向移动并且伴随能量衰减。根据式(3),当通过CCF算法从光学干涉谱中提取F-P的腔长尺寸时,解调谱中只有一个峰值。随着F-P腔长度的增加,在空气中传播的光的衰减逐渐增加,光纤芯能够捕获的光信号逐渐变弱。随着位移逐渐增大,整个CCF峰变得不尖锐,峰值也逐渐减小,很难准确地判断峰值最高点位置,导致长度超过970.55 μm的F-P腔的解调峰值变得难以定位。

图3 F-P的腔长尺寸解调数据和反射镜位移量之间的关系
为了更详细地分析本实验中PD检测到的光强与位移距离之间的关系,并确定传感系统的位移检测范围和分辨率,对位移变化产生的光谱数据进行了如下分析。
图4(a)为F-P腔长尺寸和位移长度之间的关系。位移变化量在0~900 μm之间,与腔长呈线性关系。F-P腔的长度随位移长度的增加而增加。拟合公式中的常数项表示传感器最小的相对测量距离为64.5 μm,该数值与CCF解算的最小腔长值保持一致。拟合线的斜率不等于1,因为高精度位移平台的读数存在纳米级误差。图4(b)展示了位移变化量和光强之间的关系。随着位移长度的增加,PD接收到的光强呈指数衰减。当腔长尺寸超过400 μm时,探测到的I2光能量开始趋于平缓,背景噪声与I2处在同一个数量级,使得检测到的光强度基本保持不变。值得注意的是,微弱的干涉信号仍能传输稳定的腔长尺寸信息,400~970.55 μm腔长范围下产生的干涉光信号仍可通过CCF算法解调。因此,一维EFPI位移测量系统可以测量64.52~970.55 μm的绝对距离。
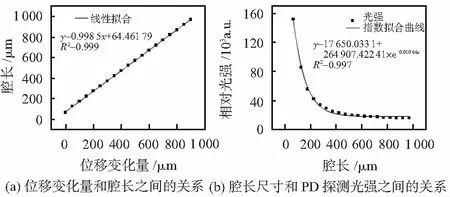
图4 EFPI传感器系统的光强随着位移变化的特征分析
位移分辨率也是EFPI传感器系统的一项关键指标。该位移测试环境在无外界振动干扰的超净间里进行。当F-P腔尺寸在64.52~970.55 μm之间时,解调算法具有相同的分辨能力,因此让EFPI结构在108~138 μm的腔长范围内往复运动,来判断传感器的位移测量稳定性和位移分辨率。图5(a)为EFPI位移测量系统在30 μm范围内的往复运动数据图。传感器探头在108~138 μm下进行步进为30 μm往复运动,每次步进时间为3 s。该传感器系统放置在纳米位移平台(SIOS,NMM—1)中,SIOS的测量和定位范围为25 mm×25 mm×5 mm,分辨率为0.1 nm。实验前,将SIOS置于初始位置状态,将反射镜安装在SIOS的位移发生装置上,光纤端面固定在金属夹具上,形成EFPI结构。将SIOS设置为每次移动30 μm,步进保持3 s,并记录大约70个数据点。传感器系统可以检测到相应的F-P腔长度变化,并且传感器系统在CCF的解调算法下,计算得到的腔长值没有发生跳变,传感器系统始终保持稳定状态。在图5(b)为位移波动分布数据图。30 μm往复运动采集的位移数据中,较大位移量处的数据点被依次提取,进行了平均差运算,方便分析测量位移的波动情况。图中发现,整体的位移波动大概在0.001~0.002 6 μm之间,并且这种纳米(nm)级的位移波动已经被传感器系统识别,SIOS系统的前端产生的机械疲劳和环境中的微弱振动导致了数据波动,产生了纳米级的微小位移误差。由此可知,该传感器的分辨率为1 nm。

图5 EFPI传感器系统性能测试
4 结 论
综上所述,本文提出了一种用于CMMs的高精度、大量程的位移探测新方法,并进行了实验验证,该方法使小型紧凑的EFPI传感器能够感测一维位移参量。其基本思想是使用镀金反射面模拟被测物体表面,利用UPC型光纤端面与被测物表面构造出非接触的反射式的EFPI结构,并将其用于高精度的表面位置测量。结合WLI原理和CCF算法形成一个简易的EFPI位移扫描探头作为新型的概念验证演示结构,有望用于三维微小轮廓定位测量领域。此外,CCF算法可以植入计算机软件中,用于快速计算位移,实现三坐标测量机的高速三维扫描。通过使用这种简单的腔长解调方式,本传感器系统在64.52~970.55 μm的范围内实现了高精度的一维微位移测量,分辨率为1 nm。除了本文报道的位移测量外,该传感器系统还可用于温度、湿度、介质折射率、声振动、加速度、气体浓度、压力、张力等因素的测量,具有非常大的潜在工程应用价值。

