考虑空间耦合的少数据风电功率预测方法

王陈恩，殷豪，陈顺，许炫淙，朱梓彬，孟安波

(广东工业大学自动化学院，广州510006)

0 引言

为实现“碳达峰”及“碳中和”，中国在2020年气候雄心峰会上提出了2030年前风电、光电装机容量超过1 200 GW的目标[1]。这预示着未来风电等新能源并网容量将会逐年增长。而风电具有很强的随机性和波动性，将对电网的备用容量、电压稳定及无功补偿造成较大的影响，危及电网的安全稳定运行。准确的风电功率预测显得尤为重要，但新建风电场的历史运行数据较少，难以准确预测，使得其考核计划难以完成，给电网、风电场带来了损失[2]。因此，提高少数据风电场的功率预测精度具有非常重要的现实意义。

风电功率预测分为物理模型[3]和统计模型[4]，物理模型主要使用气象数据和物理因素预测未来功率，理论基础坚实、性能优异，因此在实践中得到了广泛的应用，但是物理模型对数据质量的要求较高[5 - 6]。而基于数据驱动的统计学模型，如支持向量机、极限学习机等，计算效率较高、模型简单。随着人工智能技术的发展，非线性拟合能力更强的深度学习模型也被应用于风电功率预测领域，如门控循环单元网络[7 - 8](gated recurrent unit networks, GRU)、卷积神经网络[9 - 10](convolutional neural network, CNN)、长短期记忆网络[11 - 12](long short-term memory networks, LSTM)等。但上述方法均是针对数据完备的风电场，并不适用于运行时间较短的新建风电场。

仅考虑少数据风电场本身时，数据缺少的缺陷难以解决，不利于预测精度的提升。在少数据预测方面，文献[13]尝试使用生成对抗网络实现光伏功率预测，但使用生成对抗网络生成时间序列数据容易出现生成样本多样性差以及模式崩溃等问题。文献[14 - 16]使用迁移学习实现了少数据风电功率的预测，并取得了不错的预测效果，但迁移学习对源风电场的选取要求较高，并非所有风电场都拥有合适的源风电场。若在风电功率预测中，考虑风电场间存在的空间相关性，有效利用邻近风电场的特征，可以有效的改善少数据风电场功率预测存在的不足。文献[17 - 19]采用数值天气预报，结合皮尔逊相关系数等方法筛选邻近风电场的特征，获得了较好的预测效果。文献[20]采用CNN提取风电场内不同点位的关系，实现了风电场内多点位的风速预测。

在空间相关性预测方面已有大量的研究，但大多使用的是相关系数法，或采用其他较为复杂的数理统计方法[21 - 22]，并且邻近风电场的影响程度没有根据实际运行状况进行动态的调整。为提升少数据风电场功率预测的精度，本文提出了一种基于空间注意力机制(spatial attention mechanism, SA)和GRU-CSO的短期风电功率预测方法。采用空间注意力机制实现邻近风电场影响程度的自适应提取，同时根据影响程度赋予不同的权重，最后根据训练效果，采用纵横交叉算法[23](crisscross optimization algorithm, CSO)优化GRU模型的部分参数。

1 空间注意力机制

注意力机制[24 - 25]与人眼的视觉功能相似，在执行相应任务时会削弱冗余信息，将视线聚焦于影响因素较大的特征上。

为弥补少数据目标风电场数据不足的缺陷，获得不同风电场每一时刻对目标风电场的影响程度，本文采用了一种作用于不同风电场维度的空间注意力机制。通过空间注意力量化提取邻近风电场对目标风电场的影响程度。空间注意力的输入矩阵X由不同风电场特征信息构成，且输入矩阵X=[D1,D2, …,Dm]，Dm表示第m个风电场从t-1到t-n时刻不同特征构成的矩阵。Dm的表达式如式(1)所示。

(1)

由于神经网络具备强大自学习能力，利用神经网络构建空间注意力能够自适应地量化邻近风电场对目标少数据风电场的影响程度，图1为本文采用神经网络搭建的空间注意力结构。

图1 空间注意力Fig.1 Spatial attention

结合图1可知，输入X在空间注意力中的计算如式(2)—(4)所示。

w=f(WX+b)

(2)

(3)

X*=X⊙a

(4)

式中：W、b为空间注意力中全连接层的权重和偏置；f(·)为激活函数；w为未归一化的风电场权重；αi为归一化后的风电场权重；X*为空间加权后的风电场序列；且满足以下关系：w=[w1,w2,…,wi…,wm]和α=[α1,α2,…,αi…,αm]。

将α与X对应位置相乘，即得到具有不同空间关注度的序列X*，X*的具体形式如式(5)所示。

X*=[α1D1,α2D2,…,αmDm]

(5)

式中：α为邻近风电场与目标风电场影响程度的量化值，下标1～m代表不同风电场；X*为考虑空间影响程度后的序列。在X*中，不同风电场的特征均获得了与目标风电场影响程度相对应的权重，由此实现了邻近风电场与目标风电场影响程度上的量化。最后将X*作为GRU预测模型的输入。

2 考虑邻近风电场的风电功率预测模型

2.1 门控循环网络

风电功率序列作为一种时序数据存在较强的时间关联性，而GRU善于处理时间序列问题。与LSTM一样，GRU同样可以消除传统循环神经网络所存在的梯度消失及长期依赖问题，并且具备更少的训练参数[26 - 27]，图2为GRU的基本结构。

图2 GRU结构Fig.2 Structure of GRU

以空间注意力的输出X*作为GRU输入，当输入t-1时刻的风电序列时，根据GRU前向传播公式(6)可以得到t时刻的输出yt。

(6)

式中：rt为GRU的更新门；zt为GRU的重置门；Wz、Wr、WH、Uz、Ur、Uh均为不同的权重参数矩阵；br、bz、bh均为不同的偏置参数矩阵；⊗为矩阵乘法；σ为Sigmoid函数。

2.2 纵横交叉算法

纵横交叉算法是一种启发式优化算法，具有纵向和横向两个维度的交叉方式。少数据风电场历史数据较少，可能令模型在训练过程中陷入局部最优。为进一步提升模型的预测性能，在预测模型初步训练后，采用CSO算法继续优化模型中GRU输出层的权值和偏置参数构成的参数矩阵θ，如式(7)所示。

θ=[Wz,Wr,Wh,Uz,Ur,Uh,bz,br,bh]

(7)

CSO算法以初步训练后的GRU输出层的权值和偏置参数形成的矩阵θ为初始值，经过多次迭代后，即得到更优的输出层参数矩阵θ*。参数矩阵θ在CSO中的具体寻优过程如下。

1)横向交叉

参数中的父代粒子θ(i)和θ(j)随机选择第n维相互交叉得到子代Shc，计算公式如式(8)所示。

(8)

式中r1、r2和c1、c2分别为(0,1)和(-1,1)的随机数。

2)纵向交叉

参数中的父代粒子θ(q)随机选择第v维和第k维相互交叉得到子代Svc，计算公式如式(9)所示。

Svc(q,v)=r·θ(q,v)+(1-r)·θ(q,k)

(9)

式中r为(0,1)的随机数。

在每次纵向、横向交叉后，都会计算适应度函数，结合GRU模型的损失函数，在此选用均方误差(mean square error, MSE)作为CSO的适应度函数，如式(10)所示。在多次横向交叉和纵向交叉交替过程中，令粒子向适应度函数最小的方向移动，即可得到更优的输出层参数矩阵θ*。

(10)

2.3 实验流程及参数设置

本文提出的考虑邻近风电场空间耦合的少数据风电功率预测方法流程如图3所示，步骤如下。

1)数据预处理阶段，首先对风向数据进行正余弦处理，再对所有特征做归一化处理，划分训练集和测试集；

2)利用训练集对模型进行训练，得到初步训练好的预测模型；

3)采用CSO算法优化步骤2)训练所得模型中的GRU参数，以获取最终的预测模型；

4)使用测试集进行测试，并通过所选评价指标分析预测模型的性能。

图3 预测方法流程图Fig.3 Flow diagram of prediction method

针对少数据风电功率难以准确预测的问题，本文提出了考虑邻近风电场空间耦合关系的少数据风电场功率预测方法SA-GRU-CSO，通过邻近风电场的历史信息来帮助少数据风电场提升功率预测的精度。图4为该方法对应的预测模型。

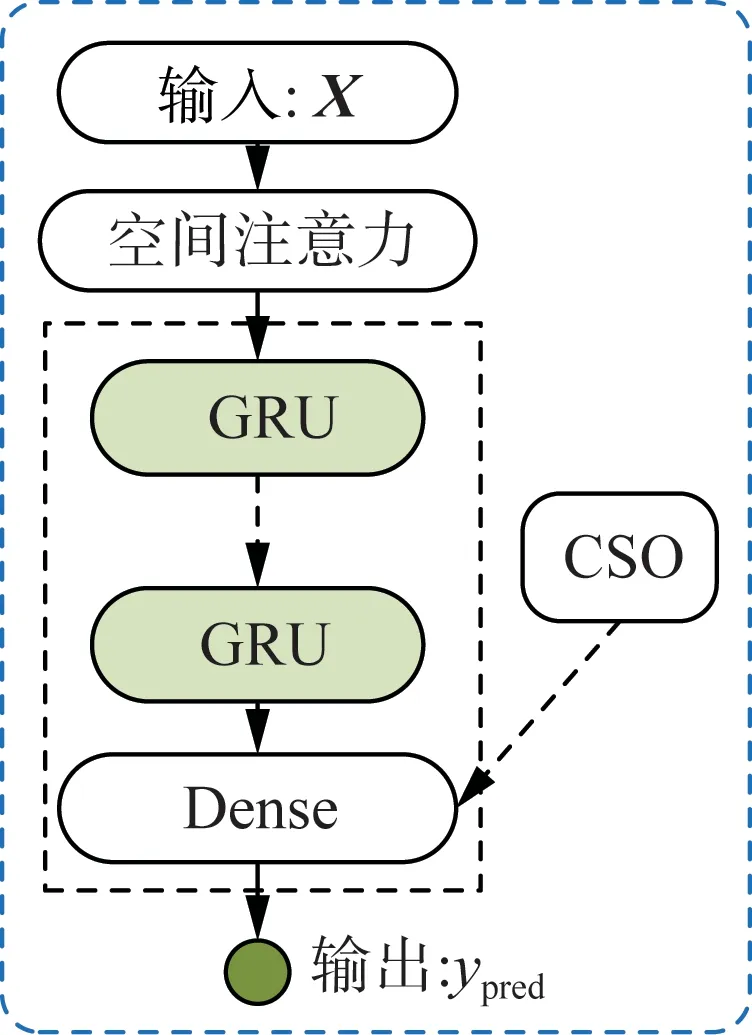
图4 SA-GRU-CSO预测模型Fig.4 The SA-GRU-CSO prediction model

本文采用两层GRU结构，分别设置为4和8，激活层采用ReLU函数，经GRU提取信息后，进入全连接层，全连接层神经元数为16，激活函数为ReLU函数，最终得到了预测结果ypred。实验中，设置迭代次数250次，采用Adam优化算法，损失函数为MSE函数，设置学习率为0.02，并将输入时间步长设置为5。根据实验验证，设置CSO的粒子种群数为25，纵向交叉率为0.6，横向交叉率为1，迭代次数为200。

3 算例分析

为验证所提方法的有效性，本文选取了位于内蒙古地区的4个风电场为实验对象，风电场详情如表1所示。本文以1号风电场为目标风电场，表2为1号风电场与其他邻近风电场输出功率的Pearson相关系数。风电场功率和天气数据分辨率为1 h，时间段为2018/12/16/00:00—2019/01/29/23:00，共计45 d。结合该地区的风力发电机高度，选取了70 m水平高度的风速、风向和温度数据。

表1 风电场情况Tab.1 Information of each wind farm

实验算例中共有风电场样本数据1 080组，在后续所有实验中，均选取前15 d的360组样本作为训练集，后30 d的720组样本作为测试集。

为减小不同特征因量纲不同带来的影响，不同特征采取不同的处理方法。对于风向数据，首先采用正弦和余弦函数处理，再将处理后的风向数据与风速和温度特征根据式(11)作归一化处理。

(11)

式中：ui*为第i个特征归一化后的值；ui为第i个特征；ui.min、ui.max分别为第i个特征的极小值和极大值。

经过归一化和正余弦函数处理后，每一组数据包含目标风电场和邻近风电场的功率、风速、温度、风速正弦和风速余弦数据。

3.1 评价指标

参照国家能源局的风电功率预测标准[28]，本文选取平均绝对误差(mean absolute error, MAE)EMAE和均方根误差(root mean square error, RMSE)ERMSE作为实验结果的评价指标,如式(12)—(13)所示。由式(12)—(13)可知，EMAE和ERMSE的值越接近于0，预测的准确性越高。

(12)

(13)

3.2 空间注意力有效性验证

为研究空间注意力对少数据风电场预测模型的作用效果以及本文所提模型的性能，分别考虑不同的预测方法，单步滚动预测未来3天的风电序列。

方法1仅考虑对少数据风电场本身进行预测，方法2、3采用Pearson相关系数选取相关性较大的风电场进行预测，方法4考虑对邻近的所有风电场进行预测，且4种方法均采用GRU进行预测。SA-GRU为本文所提方法。表2为各实验的评价指标结果，图5为空间注意力分别赋予不同风电场特征的权重。

表2 不同预测方法的指标结果Tab.2 Index results of different prediction methods

从表2可以看出，邻近风电场特征数据的使用可以有效提升少数据风电场的预测精度。相比于方法1，方法2、3、4的ERMSE指标下降了4.43%、5.39%和16.43%，EMAE分别下降了4.37%、4.93%和14.70%。由方法4与本文所提模型SA-GRU比较可知，对邻近风电场的影响程度，采用空间注意力量化能够有效地提升少数据风电场的功率预测精度，其ERMSE指标下降了41.87%，EMAE下降了46.37%。

图5为本文所提的SA-GRU预测方法中，空间注意力给予不同风电场的平均权重。1、2、3、4号风电场的权重分别为0.562、0.122、0.197和0.119。从图5中可以看出，邻近风电场的影响程度与相关系数的大小并不一致。1号目标风电场于2号邻近风电场的海拔相差近25 m，与3号风电场处于同一海拔高度上，这可能是受到风电场间地形因素的影响导致3号风电场的权重更大。而1号风电场与4号风电场直线距离61 km，海拔相差近350 m，地形差异的存在使4号风电场的权重最小。实验结果表明空间注意力能够有效量化邻近风电场对目标风电场的影响程度，提升少数据风电场的功率预测精度。

图5 空间注意力给予不同风电场的权重Fig.5 The weights given to different wind farms by spatial attention

3.3 纵横交叉算法有效性验证

为验证纵横交叉算法优化SA-GRU中GRU输出层的权值和偏重的可行性。本节对训练后的单步和多步滚动预测模型采用CSO算法进行优化，并与未优化的模型进行对比分析。表3为优化前后的指标结果，图6为CSO优化后的功率曲线图。

从表3可以看出，经过CSO优化输出层的权值和偏置参数后，预测模型的ERMSE、EMAE评价指标均得到了不同程度的提升。特别是在三步预测时，相对于不使用CSO优化的预测模型，ERMSE和EMAE指标分别下降了12.10%、17.26%。在单步预测时提升率较低，表明单步预测时，常规的梯度下降训练已经取得了不错的效果。实验结果表明，在模型训练后再次输出层的权值和偏置参数能够有效提升预测模型的预测性能。

表3 CSO优化结果Tab.3 CSO optimization results

图6 SA-GRU-CSO预测不同步数的功率曲线Fig.6 Power curves of different steps predicted by SA-GRU-CSO

4 结语

针对新建风电场历史数据较少、预测精度较低的问题，本文提出了考虑邻近风电场空间耦合关系的少数据风电功率预测方法SA-GRU-CSO，并利用实测数据进行验证。通过对该方法的理论分析和实验验证表明，该方法是可行且有效的。考虑邻近风电场特征数据后，少数据目标风电场的功率预测精度得到了提升；空间注意力机制能够有效量化邻近风电场的影响程度，并进一步提升少数据风电场功率预测的精度。