基于岭估计的系统微分响应模型率定与应用

赵建华，臧力永，施韶晖

（江苏省水文水资源勘测局宿迁分局，江苏 宿迁 223800）

0 引言

洪水预报是洪水管理中最重要、最可靠的手段之一。但在任何洪水预报系统中，由多种因素引起的不确定性有三种类型:输入不确定性、模型结构不确定性和参数不确定性。通过校正参数提高洪水预报的可靠性，是最直接有效的途径。概念性降雨径流模型具有大量的参数，参数无法直接通过测量获得。需要通过手动或使用程序进行校准获得。传统的优化算法，例如：梯度下降法、牛顿法、单纯形法等局部优化方法已被证明难以寻找到最优解。随着计算机技术的发展，人工智能算法得到了很大的发展，这些算法如遗传算法、粒子群算法、蚁群算法、SCE-UA算法等，被广泛地运用于水文模型参数优化中，但此类方法的收敛性仍未得到证明。近年来，河海大学包为民教授提出了系统微分响应参数率定方法，该方法在新安江模型、SAC 模型、VIC 模型、SWAT 模型的参数优化中都取得了较好的结果。但相关研究结果表明，该算法在一些特定问题求解过程中存在问题，因此出现了相应的改进方法，如通过总体最小二乘的岭估计解法改进系数矩阵的病态问题。文章将岭估计-系统微分响应法应用于新安江模型参数优化求解，探究验证其在水文模型参数率定中的适用性。

1 研究方法

1.1 新安江模型

新安江模型是赵人俊提出的概念性水文模型，其在中国大部分地区，尤其是湿润和半湿润地区的水文预报工作中得到了广泛的应用。文章采用的新安江三水源模型，蒸散发计算采用三层蒸散发模型，产流计算采用蓄满产流方法，坡面汇流采用线性水库法，河网汇流采用马斯京跟法。需要率定的模型参数共有16 个，在具体实际应用中，蒸散发参数K，产流参数WM、B，水源划分参数SM、EX、KI、KG，汇流参数CI、CG、CS对模型输出结果较为敏感，因此在模型模拟式应主要对这些敏感参数进行率定。而其他参数主要根据区域地理水文特征确定，一经确定就无须改变。

1.2 基于岭估计-系统微分响应的参数率定方法

将水文模型概化为：

式中：Q（t）为模型计算得到的出口断面流量；θ为模型参数；X（t）为模型输入自变量。

在率定模型参数时，将模型参数看作自变量，对函数模型f进行线性化，即一阶泰勒展开。其表达式为：

式中：Q（X，t）=［Q1，Q2，…，Qn］T为实测出口断面流量序列；f（θj，X（t））=［Qc1，Qc2，…，Qcn］T为计算出口断面流量序列；E=［e1，e2，…，en］T为流量观测误差序列；U为灵敏度矩阵，即函数偏导数矩阵。

根据岭估计最小二乘原理，可以得到：

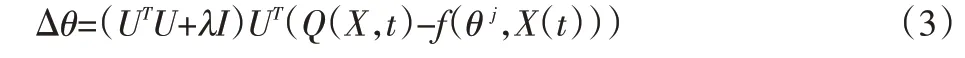
式中：I为单位矩阵；λ为正则化参数，用来平衡解的不稳定性和光滑性。文章采用S折交叉验证法来确定此参数，更新后的参数为：

式中字母含义同上。

1.3 模型精度评价指标

日模型模拟中选取年径流深相对误差、日流量过程的Nash-Suttcliffe系数来评定模型的精度。

年径流深相对误差计算公式：

式中：R为径流深相对误差（%）；Rs为模拟的径流深（mm）；RO为实测径流深（mm）。

Nash-Suttcliffe系数计算公式为：

式中：NSE 为确定性系数；Qc（i）为计算流量（m3/s）；QOb（i）为实测流量（m3/s）；N为模拟的序列长度。

2 淮河上游新安江模型率定与应用

2.1 研究区概况

淮河区包括淮河流域及山东半岛，地处中国东部，介于长江和黄河之间，面积33 万km2。流域多年平均降水量为800～1 400 mm，多年平均水面蒸发量为800～1 000 mm，多年平均径流深约为371 mm。文章选取淮河上游大坡岭水文站以上流域，研究区为中国半干旱气候与湿润气候过渡带，流域面积1 631.22 km2。对研究区数字高程资料进行处理，得到了以下研究区数字高程图，见图1。

图1 大坡岭流域高程图

区域内以山区和丘陵为主，共有固庙站、桐柏站、二道河站等共13个雨量站，有南阳站、枣阳站、驻马店站、信阳站4个气象站点，研究区内多年平均降水量约939 mm，多年平均径流深约375 mm。

2.2 理想模型率定效果分析

为检验基于总体最小二乘的岭估计解法的系统微分响应参数率定方法在新安江模型中的适用性，构建新安江理想模型进行参数率定。文章随机设置了一套参数真值，见表1。将实测输入数据和参数真值带入模型，得到的输出径流过程即为“真实的”径流过程。对需要率定的敏感参数设置初始值，利用于基于总体最小二乘的岭估计解法的系统微分响应参数率定方法进行参数率定。

表1 理想模型参数真值表

在对参数K、SM、KG、CS、CI、CG 进行率定时，给定不同的初始值都能收敛到同一结果，且迭代次数较少。由于岭估计解法的原理是通过在损失函数的基础上增加L2 正则项，目的是为了防止最小二乘法导致地过拟合问题。所以参数率定最终的收敛值与给定的真值稍有偏差，如CI最后收敛到0.92，但总体而言各参数均能收敛到参数真值附近。利用最终率定得到的参数解进行径流模拟，径流深相对误差仅为0.80%，确定性系数高达0.99。综上，基于岭估计-系统微分响应的参数率定方法，其具有高效、稳定的特性，能够有效地对新安江模型的参数进行优化求解。

2.3 淮河上游新安江模型率定与径流模拟

基于大坡岭流域内2002-2009 年13 个降雨站点的日降雨资料和大坡岭水文站的日流量资料对日尺度新安江模型进行参数率定和验证。以2002-2007 年为率定期，2008-2009 年为验证期。通过计算径流深相对误差和确定性系数对率定结果进行评价，见表2。

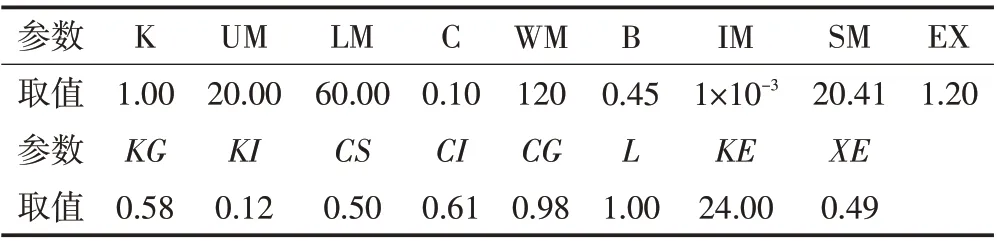
表2 大坡岭流域率定期参数率定结果表

由表3可以看出，率定期及验证期的日尺度模拟结果均满足精度要求，率定期6 a以及验证期2 a的确定性系数均在0.70以上，年径流深相对误差均在10%以内。而相对于率定期，验证期的模拟精度有所提高，这表明采用基于总体最小二乘的岭估计解法的系统微分响应法率定得到的参数具有可信度，该方法适用于新安江模型的参数率定。在2002、2003、2008 年的径流模拟中，模拟的流量峰值略大于实测的，这可能与模型本身参数和结构的局限性等因素有关。

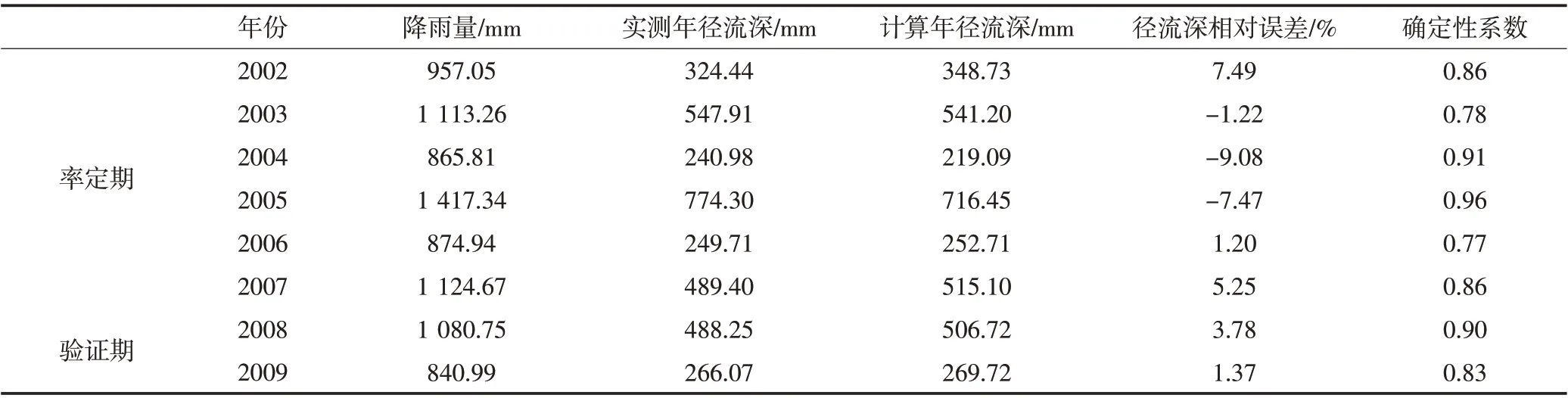
表3 大坡岭流域2000-2009日尺度径流模拟结果表

3 结论

文章将岭估计-系统微分响应参数率定法结合新安江模型应用于大坡岭流域日尺度径流模拟。得出以下结论：①理想模型的应用检验表明，在给定不同初始值的情况下，新安江模型的敏感参数均能收敛到同一值附近，由于算法本身具有防止过拟合的特性，收敛值近似等于参数真值，与真值稍有偏差，但总体率定结果较好；②实际流域应用结果表明用基于岭估计-系统微分响应参数率定方法率定新安江模型参数是可行的，率定结果合理且十分高效。