深度强化学习在翼型分离流动控制中的应用

姚张奕，史志伟，董益章

南京航空航天大学 非定常空气动力学与流动控制工业和信息化部重点实验室，南京 210016

0 引 言

人类大脑理解、分类信息并进行学习的过程一直是人们研究的热点。在人工智能（AI）研究领域，创造出一种能够像人类大脑一样自行学习决策的算法是科学家研究的重要目标。追溯到20世纪80年代末，Sutton提出的强化学习（RL）算法框架给出了可行性答案。在这个框架中，智能体通过与环境进行互动获得奖励来积累经验、自我学习。

近年来，深度神经网络的兴起给强化学习提供了强大的新工具。深度学习与强化学习的结合，称为“深度强化学习（DRL）”，其通过深度神经网络对高维状态空间进行特征提取和函数拟合，消除了经典强化学习的主要障碍。当前，DRL 在多个领域都展现了前所未有的强大潜力，不但能够进行机器人控制和自然语言处理，还在多种游戏（Atari 游戏、Go、Dota II、Starcraft II、Poker等）中都达到了高手的水平。与此同时，DRL 也被应用到工业中，如韦夫（Wayve）公司通过实验和仿真来训练自动驾驶汽车，Google 使用DRL 来控制其数据中心的散热。

流动分离作为流动控制中的经典问题，一直是学者们研究的热点。对机翼分离流控制技术的研究主要集中在边界层吹吸气控制方面。吹气控制方式主要有直接吹气（含非定常吹气和微量吹气等）控制和前缘缝翼控制2 种。Chng 等对Clark-Y 翼型进行吹吸气控制，将吹气控制装置设置在翼型前缘附近，沿流向吹气，将吸气控制装置设置在翼型后缘附近，沿流向吸气；实验结果表明，进行吹吸气控制后，翼型的流动分离被抑制，气动特性明显提升。Coiro 等对机翼表面的分离流动采用非定常吹气控制进行研究，将非定常吹气装置安装在机翼上表面的中间部位，总结了无量纲激励频率和动量系数对非定常吹气控制效果的影响，将实验结果与数值模拟结果对比，证明该吹气控制方式具有良好的控制效果。

近年来，深度强化学习也被应用在流动控制领域。Verma 等使用DRL 模拟鱼群在复杂流场中的游动，训练出一个“聪明的游泳者”，能通过调整自身位置和身体变形与迎面而来的涡流动量同步，提高游泳效率。东京大学的Shimomura 等在NACA-0015 翼型上采用介质阻挡放电（Dielectric Barrier Discharge，DBD）等离子体激励器对翼型进行了闭环分离控制实验，采用DRL 算法对激励器的激励频率进行优化选择，证明在不同迎角下使用DRL 算法训练的网络可以选择最优频率。Guéniat 等对圆柱绕流控制进行了尝试，在仿真环境下使用RL 算法对流动进行控制，实现了减阻的效果。Pivot 等采用计算仿真方法，模拟低雷诺数（Re=200）二维圆柱绕流流场，通过RL 算法控制圆柱的自旋转从而抑制尾迹区的流动，达到减阻目的（减阻率约为17%）。Xu 等在圆柱后方上下布置2 个相同的小圆柱，在Re=240 时使用DRL 算法训练网络，通过控制小圆柱的自旋转来抑制尾流的分离。Rabault 与Tang等也采用计算仿真方法模拟了低雷诺数下二维圆柱绕流流场，通过在圆柱上下端点处加装射流孔，对圆柱进行零质量射流控制；仿真结果表明，使用DRL 算法训练的网络成功地稳定了卡门涡街，且圆柱受到的阻力也降低了约8%。由此可见，深度强化学习正作为一种可行的控制策略，逐渐与流动控制领域的研究相结合。

本研究的目的是设计一种基于深度强化学习算法的闭环控制系统，该系统可以根据流场中的翼型表面压力系数选择合适的前缘吹气量，抑制大迎角下的流动分离，实现非定常吹气，减小系统的吹气量。实验中，NACA0012 翼型以固定的迎角放置于流场中，选择深度强化学习中性能优异的TD3（Twin Delayed Deep Deterministic Policy Gradients）算法作为控制系统的核心驱动，由压力传感器测得的表面压力实时数据以及智能体自身的动作输出作为神经网络的输入数据，通过迭代实验使智能体自我学习抑制流动分离的最佳控制策略。

1 实验方案

1.1 实验设置

实验在南京航空航天大学（NUAA）非定常空气动力学实验室的1 m 非定常低噪声低湍流度风洞中进行。风洞为开口风洞，实验段开口为1.5 m（宽）×1.0 m（高）。实验模型为二维NACA0012 翼型，弦长200 mm，展长400 mm，模型上表面布置了6 个测压孔，测压孔均匀分布在机翼中部，相邻孔之间的距离为20 mm，与前缘的距离分别为弦长c 的20%、30%、40%、50%、80%、90%，如图1所示。实验风速10 m/s，基于弦长定义的雷诺数为1.36×10，机翼迎角16°。射流激励器采用沿翼型上表面均匀吹气的形式，气体从模型侧边通入，经一级缓冲区和二级缓冲区（设2 个缓冲区的目的是保证激励器出口气体速度基本一致），从翼型上表面吹出。激励器的位置如图1所示，与前缘的距离为弦长的10%，射流缝高1 mm，射流出口方向与翼型弦线成30°夹角。射流出口速度由电磁比例阀（PVQ 系列）进行无级控制，控制频率为100 Hz，出口速度与电磁比例阀控制信号（即电压信号）正相关，范围为0～22 m/s，如图2所示。机翼表面的压力系数由动态压力传感器（MS4515DO 系列）通过测压孔测得，采样频率为100 Hz，准确度为±0.25%。本文通过补偿微压计给出9 个标准压力点，使用压力传感器进行了7 次重复性测试，绝对误差为±0.2 Pa，如图3所示。

图1 翼型截面Fig.1 Airfoil section view

图2 电压与射流出口速度对应关系Fig.2 Correspondence between voltage and jet velocity

图3 传感器重复性测试Fig.3 Sensor repeatability test

1.2 深度强化学习

强化学习通常被定义为在马尔科夫决策链（MDP）下寻找最优策略从而获得最高累积奖励的问题。马尔科夫决策链可以由1 个元组（，，P，）表示，其中S 和A 分别表示状态空间和动作空间；P为状态转移分布，表示在状态s 下采取动作a 后转移到新状态s的概率分布；R 表示在状态s 下采取动作a 后获得的奖励。

图4 强化学习的基本框架Fig.4 The basic framework of reinforcement learning

强化学习的目的就是要找出最佳的策略π，从而最大化长期回报（）=E[]。其中，表示策略的相关参数，p则是MDP 中的状态转移分布。因此，学习的目标是找到一组参数（*）可以使目标函数J（）最大化。策略梯度法是通过估计∇J（），然后执行梯度上升算法找到网格参数*。∇J（）可以估算为：

式中，Q（s，a）表示从s开始行动、遵循策略做出动作a后获得的预期回报，一般称之为Q 函数。与之相关的还有值函数V （s），表示从s开始、遵循策略所能获得的预期回报。Q 函数与值函数的相关表达式以及它们之间的关系如下：

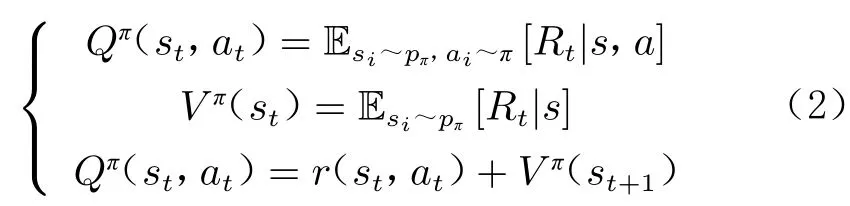
本研究采用的深度强化学习算法为TD3 算法。该算法包含了6 个深度神经网络（1 个Actor 网络、2 个Critic 网络以及各自对应的Target 网络）。TD3算法设置2 个Critic 网络，可有效缓解Q 函数值（简称Q 值）高估的问题，延迟Actor 网络的更新，减少积累误差，从而降低方差。此外，还引入了一种SARSA 型正则化技术，通过改变时序差分目标自举出相似的状态动作对。

1.3 基于深度强化学习的控制策略控制

图5为翼型流动分离的闭环控制系统示意图，图中C为压力系数。在实验中，状态空间分为2 种：第1 种是翼型上表面距前缘40%、90%弦长位置的压力系数；第2 种在第1 种的基础上额外增加智能体的动作输出，即将智能体的动作输出也纳入到观测环境中。为了提高智能体的动态性能，智能体的输入不仅包括当前时刻的观测量S，还会往前追加4 步，即智能体的实际观测量为{S，S，S，S，S}。动作空间为施加在电磁比例阀上的电压，体现为射流出口速度。射流激励器的控制信号为0～5 V，对应的射流出口速度为0～22 m/s；激励器的控制频率为100 Hz。

图5 闭环控制系统示意图Fig.5 Schematics of the closed-loop control system

后缘附近的压力系数能够反映流动分离是否被抑制。当气流附着到机翼表面时，由于压力恢复，后缘的压力系数C会接近于零。因此，奖励值R通过机翼后缘处（距前缘90%弦长）给出，奖励函数可设置为2 类：

第1 类为离散型奖励函数：

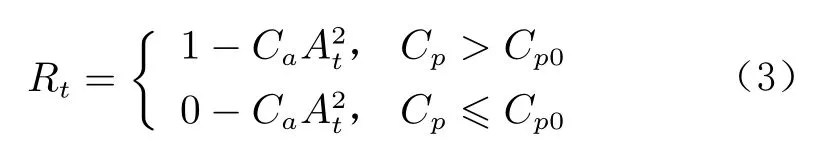
式中，C为惩罚系数，C为函数分段点。依据流动分离是否被抑制，将奖励离散为0 和1，同时附加一个额外的惩罚项CA，用于惩罚吹气量的大小，输出动作越大，惩罚项会越大。图6显示了迎角16°时，距前缘90%弦长处的压力系数的时间变化图。图中，射流激励器在第4 s 时以最大的动作（5 V）启动，压力系数从–0.50 增加到–0.05，流动分离被抑制。根据该结果，将C设定为–0.30，当距前缘90%弦长处压力系数大于–0.30 时，可以认为流动分离已经被抑制或者一定程度上被抑制。

图6 翼型后缘压力系数随时间变化Fig.6 Time variation of the pressure coefficient of the airfoil trailing edge

第2 类为连续型奖励函数：

当后缘处的压力系数C越接近目标压力系数C时，智能体得到的奖励值越接近于0；当后缘处的压力系数C越偏离目标压力系数C时，智能体会得到一个更大的负值；同时，智能体还附加有吹气的惩罚量。

离散型奖励函数的目标是抑制翼型的流动分离，而连续型奖励函数的目标则是希望对后缘处的压力系数进行精确控制。

图7展示了智能体的简要学习流程，图中L（）为网络参数的损失函数。每一个完整的时间步包含了控制部分和训练部分。在开始的时间节点上，智能体根据测压孔测量的翼型表面压力系数S和Actor 网络给出的电磁比例阀控制信号A来控制翼型前部的射流速度；在结束的时间节点上测得翼型表面压力系数S，根据设置的奖励函数返回一个奖励值R；将{S，A，R，S作为一组数据存入经验池B 中。训练部分即从经验池中随机选择一批数据用于神经网络的学习，对Actor 网络和Critic 网络进行参数更新，而Target 网络则根据相应网络参数的变化进行平滑更新。

图7 智能体简要学习流程Fig.7 TD3 algorithm learning process

2 结果与讨论

在实验中，对于训练的智能体而言，训练前没有获得任何的先验知识，初始化的智能体输出在给定输出范围的中值（2.5 V）附近。实验每一幕为500 个时间步，即5 s。每一幕的总奖励值被定义为500 个时间步获得的总奖励值。在训练过程中，由于每一次输出动作都会附加一个随机噪声，总奖励值并不能准确地表示智能体的性能，因此在每训练20 幕之后增加测试环节。由于奖励函数不同，智能体每一幕获得的总奖励值也不尽相同，因此下文中的总奖励值均经过统一化处理，以离散型奖励、C=0010为计算方式。实验探究了观测量改变（2 种方式，即仅以翼型表面压力数据作为观测量或将翼型表面压力数据和智能体自身动作一同作为观测量）对智能体性能的影响，获得了离散型奖励和连续型奖励下智能体的训练效果，最后对训练完成的智能体在其他迎角和风速下的控制效果进行了测试。

2.1 奖励值的变化趋势图

图8显示了惩罚系数C=0.010 时、离散型奖励下测试环节总奖励值随幕数的变化规律。在训练初始阶段，由于初始化的智能体输出动作在2.5 V 附近，射流出口气体速度低，不能抑制翼型的流动分离，无法获取流动再附带来的奖励收益，因此智能体更趋向于降低吹气量以减小吹气惩罚，每一幕的总奖励值一直徘徊在0 附近。直到某一刻，一个巨大的动作噪声将输出动作带到了5.0 V 附近，射流吹气量陡然增大，流动分离被抑制，智能体学到了有益的经验，总奖励值便开始上升，随后稳定在250 左右。如图9所示，此时在智能体的控制下，翼型表面靠近后缘处的压力系数在–0.50～0 之间波动，输出动作开始周期性变化，但是动作集中在0 V 附近，智能体倾向于少吹气。如图8所示，在60 幕的时候，智能体达到了当前参数设置下的最佳控制策略，随后奖励值又开始下降。

图8 测试环节总奖励值随幕数变化Fig.8 The total reward value of the test session varies with episodes

图9 第20 幕测试下翼型后缘压力系数和输出电压随时间变化Fig.9 Time variation of the pressure coefficient of the airfoil trailing edge and the output voltage at twentieth episode

2.2 仅观测压力数据的控制结果对比

图10 展示了仅以翼型表面压力系数为观测量时、在不同惩罚系数下翼型表面后缘处压力系数随时间的变化和智能体输出动作随时间的变化。由于奖励函数不同，相同时序后缘压力系数在不同奖励函数下获得的奖励也有所不同（图中的总奖励值均经过统一化处理）。可以看出：当惩罚系数C=0 时，即对智能体的输出动作不存在惩罚时，智能体毫不犹豫地选择了以最大动作5.0 V 输出，抑制了流动分离；而相对于定常吹气，周期性的激励肯定是更好的选择，但是当奖励函数中不存在动作的惩罚时，智能体无法学到该控制律。当惩罚系数C升高至0.005 时，惩罚项开始对智能体的控制策略产生影响，翼型后缘压力系数稳定在–0.30 以上，这表明翼型的流动分离得到抑制，并且动作输出开始周期性波动，波动的区间限制在2.0～5.0 V。当惩罚系数C=0.010 时，训练出的智能体达到了最好的性能表现，输出动作从0 和5.0 V 开始周期性波动，无量纲激励频率F=0.13。将智能体10 s 内的动作输出进行加权平均后，吹气量比定常吹气（5.0 V）减少约52%。当惩罚系数增大至0.020 时，由于惩罚项的占比过大，智能体难以逃脱低输出带来的低惩罚，陷入局部最优难以跳出，智能体的控制策略更倾向于集中在0 V 附近，控制效果不理想。

图10 不同惩罚系数下翼型后缘压力系数和输出电压随时间变化Fig.10 Time variation of airfoil trailing edge pressure coefficient and output voltage with different Ca

图11 展示了将奖励函数设置为连续奖励时、在智能体控制下翼型表面后缘处压力系数随时间的变化和智能体输出动作随时间的变化。将奖励连续化后，数值上与离散型奖励相差了一个数量级，因而也将惩罚系数减小了一个数量级，奖励函数R=-|C-（020）0001。由图可见，连续型奖励设置下的智能体也训练出周期性的激励，但是并不能将后缘处压力系数稳定在目标值–0.20 附近，波动范围很大；但是，它也可以将翼型后缘压力系数控制在–0.30 以上，只是输出动作在1.6～5.0 V 之间波动，总奖励值略低于离散型奖励下的控制策略。

图11 连续奖励函数下翼型后缘压力系数和输出电压随时间变化Fig.11 Time variation of continuous reward function airfoil trailing edge pressure coefficient and output voltage

由此可见，不论是离散型奖励，还是连续型奖励，仅以翼型表面压力数据作为观测量，训练出的智能体并不能很好地达到效果。在强化学习中，对算法性能影响较大的因素是决策链的马尔可夫性质。马尔可夫性质表示系统下一个状态只和当前状态有关，而与之前的状态无关。换言之，根据当前的观测量加上动作量就可以完全确定未来状态轨迹的分布。而在真实的动力学系统中，由于存在实验时间延迟以及误差，系统真实状态无法被完全且准确地获取，进而导致决策链的非马尔可夫性质。下面将在观测量中引入智能体以往采取的动作量，进一步增强系统的马尔可夫性质，并对控制结果进行讨论。

2.3 压力数据与控制动作一同作为观测量的控制结果对比

将智能体自身的动作输出加入到观测量，即观测量变为0.04 s 内翼型表面压力数据以及智能体自身动作输出的时间序列。图12 展示了将动作加入观测量后离散奖励函数下不同惩罚系数对智能体最终训练结果的影响。可以发现，当惩罚系数C= 0.010时，智能体表现出了更加严格的周期性控制，控制频率更高，并且压力系数稳定在–0.10 以上，与定常吹气（5.0 V）效果基本一致，但吹气量更少，为定常吹气的50%。而当C=0.020 时，智能体则表现出了极致的贪婪，在满足C＞ –0.30 的前提下尽可能地减少吹气，当压力系数开始下降并将降至–0.30 时，智能体才会提前进行一次5.0 V 的动作输出，将压力系数拉回。图13 对2 种控制律进行了傅里叶变换，可以发现，当C=0.010 时，傅里叶变换后的幅值P 只有一个峰值，对应的无量纲激励频率F=0.50，这表明智能体训练出了一种固定单一频率的控制律，这种周期性激励方式是抑制翼型流动分离的一种典型控制律。当C=0.020 时，对控制律进行傅里叶变换后，没有确定的主导频率，存在多个频率共同作用。

图12 离散奖励函数、不同惩罚系数下翼型后缘压力系数和输出电压随时间变化Fig.12 Time variation of airfoil trailing edge pressure coefficient and output voltage with different Ca under discrete rewards

图13 不同控制律的傅里叶变换Fig.13 Fourier transform of different control laws

图14 展示了将奖励函数设置为连续奖励时，不同目标压力系数C下智能体控制的翼型表面后缘压力系数随时间的变化和智能体输出动作随时间的变化。可以看出，当C为-0.10 和-0.20 时，智能体可以将翼型后缘压力系数稳定地控制在C附近。当C=010时，后缘处（0.9 c）压力系数起初会有一点超调量，随后便稳定在010附近，上下波动不超过±0.03。当C=020时，智能体也可以将后缘处（0.9 c）压力系数控制在020附近，上下波动在±0.05 以内。将2 种控制律进行傅里叶变换后（图15）可以发现，两者都有一个主导频率（即F≈0.66），不同的是两者主频的幅值。当C=010时，在F=0处幅值P=4.0 V，而C=020时的P=3.0 V，说明2 种控制律在基准动作上也有所不同。与仅将压力系数作为状态输入相比，加入动作量状态输入后，智能体的性能大大提升，能够根据奖励函数的设置将压力系数稳定在目标值附近。

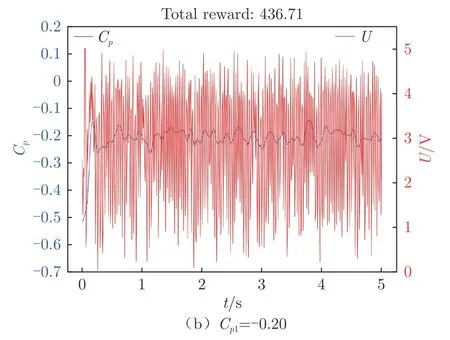
图14 连续奖励函数下翼型后缘压力系数和输出电压随时间变化Fig.14 Time variation of continuous reward function airfoil trailing edge pressure coefficient and output voltage

图15 不同控制律的傅里叶变换Fig.15 Fourier transform of different control laws

图16 为智能体在不同迎角与风速条件下的性能表现。智能体是在迎角16°、实验风速10 m/s 的状态下进行训练的，目标压力系数C=–0.20。训练完成后，将迎角调节为15°和17°，或将实验风速调整为8 和12 m/s。 由图16（a）～（c）可以看出，在改变风速和降低迎角的情况下，智能体可以将翼型后缘压力系数稳定控制在C附近；相较于训练工况，测试工况压力系数波动较大；不同状态下，输出的控制律也有所不同。由此可见，通过训练的智能体具备良好的泛化能力。但是在增大迎角的情况下（图16（d）），智能体的泛化能力减弱，不能完成后缘压力系数稳定控制的任务。

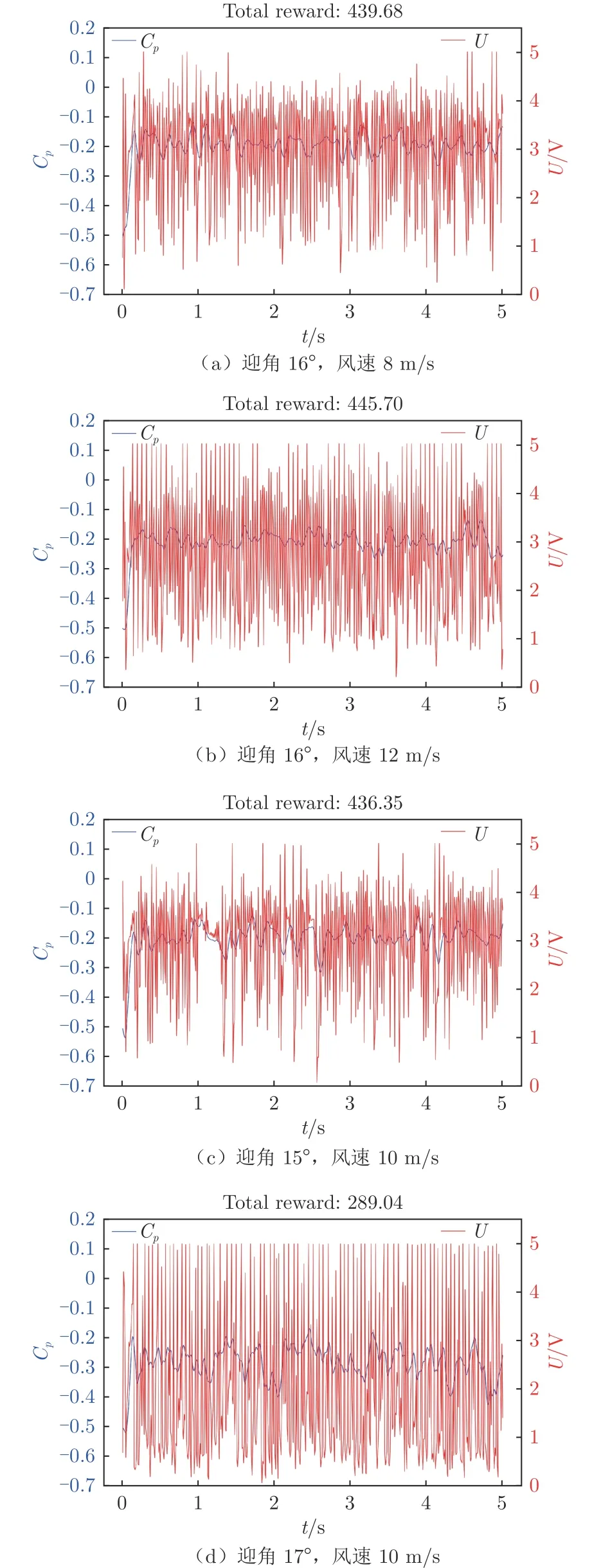
图16 不同迎角与风速下翼型后缘压力系数和输出电压随时间变化Fig.16 Time variation of airfoil trailing edge pressure coefficient and output voltage under different angles of attack and wind speeds

3 结 论

本文将深度强化学习应用在翼型分离流的主动控制实验中，在无需获取翼型模型的情况下，其能够根据奖励函数完成不同的控制任务。实验研究了基于深度强化学习算法的射流激励器在NACA0012 翼型上的闭环流动控制，对比了不同状态输入和不同奖励函数对控制效果的影响。结果表明：

1）基于DRL 算法的闭环控制系统可以实现大迎角下流动分离的抑制，并且是在没有任何先验知识的情况下完成了控制律的训练。与定常吹气相比，训练出的非定常吹气可以在满足抑制分离的条件下减少50%的吹气量。在训练过程中，DRL 算法不仅能训练出典型控制律，还可以发现新的控制方案。

2）奖励函数的设置对于智能体的训练效果有很大的影响。离散型奖励中，惩罚系数的大小直接影响智能体的策略；而采用不同的奖励（离散型和连续型奖励）也会导致控制效果的差异。

3）对于机翼大迎角流动分离这类准周期运动，将动作量加入观测量可以极大地改善智能体性能。加入动作量后，离散型奖励可以训练出更高频率的控制律，此外还可以在满足条件的情况下尽可能地减小吹气量；连续型奖励训练出的智能体可以将后缘压力系数稳定控制在目标值附近，这是开环控制难以做到的。在改变风速和降低迎角的情况下，智能体具有良好的泛化能力。