基于粒子群算法的固定时间多约束无人机轨迹规划
邵士凯 石伟龙 杜云








摘要:針对粒子群算法在轨迹规划时,将无人机视为质点,未考虑无人机的飞行时间、角度等参数的不足,提出一种数值方法结合粒子群算法的轨迹规划求解方法。首先,考虑到对每个时刻控制变量进行优化会耗费大量的时间,将无人机的飞行时间离散为一定数量的切比雪夫配点,在这些离散的配点处优化控制变量以减小计算负担;其次,将角速度作为控制变量,运用曲线拟合求解出角速度与时间的函数,经过积分求出无人机的角度、位置与时间的函数;再次,将结果代入粒子群优化模型并结合无人机运动学模型进行优化求解,根据分配的时间计算出最终的角速度、角度以及位置坐标;最后,在复杂环境下进行无人机轨迹规划仿真,通过与已有方法的对比,验证所提求解方法的有效性和可行性。结果表明,所提出的轨迹求解方法可以求出包括位置在内的各个运动学参数,规划出光滑的轨迹并且成功避开前进过程中的障碍物。所提方法有效提升了轨迹规划的求解维度,对实现智能自主化飞行有一定的参考价值。
关键词:航空、航天科学技术基础学科其他学科;轨迹规划;无人机;粒子群算法;运动学模型;曲线拟合
中图分类号:TN958.98文献标识码:A
DOI:10.7535/hbkd.2022yx03005
Fixed time multi-constraint UAV trajectory planning based on particle swarm optimization
SHAO Shikai SHI Weilong DU Yun
(School of Electrical Engineering,Hebei University of Science and Technology,Shijiazhuang,Hebei 050018,China)
Abstract:In view of the disadvantage that UAV is usually regarded as a particle in trajectory planning with particle swarm optimization algorithm,the flight time,angle and other parameters of UAV are ignored,a trajectory planning method combining numerical method with particle swarm optimization algorithm was proposed.Firstly,considering that the optimization of each control variable will cost a lot of time,the flight time of UAV was discretized as a certain number of Chebyshev points,and control variables were optimized at these discrete collocations to reduce the computational burden.Secondly,the angular velocity was taken as the control variable,the function of angular velocity and time was solved by curve fitting,and the function of angular and position of UAV with time was obtained by integration.Thirdly,the angular velocity,angle and position were calculated according to the allocated time.Finally,the simulation of UAV trajectory planning in complex environment was carried out,and the effectiveness and feasibility of the proposed method were verified by comparing the Monte-Carlo simulation results with the results of existing methods.The results show that the proposed method can calculate the kinematic parameters including position,plan a smooth trajectory and successfully avoid the obstacles in the process of forward.Therefore,the combination of particle swarm optimization algorithm and numerical method can solve the kinematics parameters of UAV and provide certain reference value for the improvement of the solution dimension of trajectory planning and the realization of intelligent autonomous flight.
Keywords: basic science and technology of aeronautics and astronautics other disciplines;trajectory planning;UAV;particle swarm optimization (PSO);kinematic model;curve fitting
随着科技的不断创新,无人机已经广泛应用于军事和民用任务,如情报、监视、侦察、救援和商业表演[1-3]。作为无人机研究领域的重要方向之一,无人机轨迹规划备受关注。
经过众多学者的不断探索,无人机轨迹规划算法的研究成效显著。基于图形的算法是一种简单的路径规划方法,如:Voronoi图算法[4]、A*算法[5]、概率路线图算法[6]、快速探索随机树算法[7]以及人工势场算法[8]。然而,这些算法很少考虑无人机的运动学和动力学约束,因此通常不能应用于实际情况。另外,这类算法都是基于代价图实现的,需要提前生成和存储代价图,而代价图的生成非常耗时。近年来,随着群体智能技术的发展,基于生物群体的进化算法取得了很大的进步[9],它们保持了较强的搜索能力,能够以更高效、更灵活的方式搜索最优解。利用这种方法进行无人机路径规划越来越受到研究者的重视。常用的算法主要有人工蜂群算法(artificial bees colony algorithm)[10]、[JP2]蚁群算法(ant colony algorithm)[11]、遗传算法(genetic algorithm)[12]和粒子群算法(PSO)[13]。在这些算法中,粒子群算法相对于其他算法具有通用性强、搜索效率高、迭代公式和算法规则简单、易于仿真实现等优点[14-15],应用于无人机航线规划求解后取得了一定成果[16-18]。
上述智能算法虽可快速规划出可行轨迹,但仍有不足之处,如易陷入局部最优、未考虑无人机的实际飞行性能需求等,导致其轨迹规划结果只具备粗略的指引作用。为提高轨迹的求解精度,一些学者采用数值方法将求解的参数维度由三维拓展到四维,进而,求解结果可直接作为无人机系统的参考指令,大大降低了飞行控制系统的复杂度。文献[19]针对高超声速飞行器,在多约束条件下,设计了基于Dubins曲线的轨迹规划算法,仿真结果表明所提方法可产生满足约束的飞行轨迹。文献[20]提出了一种基于伪谱法的轨迹规划方法,采用非线性规划方法有效解决了轨迹优化问题。但数值方法仍存在较大局限性,随着问题维数的提升、复杂程度的提高,数值方法会出现耗时长、收敛速度慢,甚至无法求得有效解等问题。因此,综合群智能算法和数值法的优点,将群智能算法与数值方法结合实现轨迹规划是一个值得研究的问题。文献[21]将控制变量和时间分别离散取值并结合粒子群算法提出了一种新的轨迹规划求解方法,有效解决了轨迹规划的优化问题。然而,文献[21]主要是将飞行时间平均分配,控制输入接近分段常数值,而且采用二维的运动学模型,因此该求解方法存在一些局限性。文献[22]针对无人机与水下无人航行器协同攻击目标的问题提出了一种对控制变量进行优化的粒子群算法,最终提出的路径规划方法能够生成协同路径,所得结果与理论最优解非常接近,但是在轨迹优化的求解方法上只提出了一个大体框架以及一些仿真验证,没有阐明具体的求解方法。
针对粒子群算法以及已有方法的不足,本文提出一种新的轨迹规划求解方法,在固定时间且多约束的条件下,将传统的仅包含位置的三维航线规划扩展为包含飞行时间和多种状态约束的四维轨迹规划。
1问题描述与模型建立
1.1问题描述
针对无人机在复杂环境下的轨迹规划问题,考虑到目标点、障碍区域已由卫星与高空雷达探测得知,且本文假设无人机匀速飞行。因此,影响任务完成的关键在于:1)如何将飞行时间合理分配给各个配点;2)如何求解粒子群算法与无人机运动学模型的耦合关系,获取多维度航线指令,为飞控系统提供良好参考;3)如何保证整体航线的最优性,如距离最短、性能指标最优等。无人机在复杂环境下轨迹规划示例如图1所示。
1.2无人机运动学模型的建立
在轨迹规划问题中,通常将载运工具视为质点,采用质点运动模型,计算其行动轨迹,甚至在一些文献中只考虑了质点运动学模型[23]。这是因为相较于控制器模块,轨迹规划模块相当于外回路,需要为内回路提供控制指令信号,所以需要有较快的运算速度。轨迹规划问题中载运工具通常视为刚体,其运动模型由1组变系数非线性微分方程描述,求解此方程组需要耗费一定时间。为了进一步节约时间,本文采用简化后的无人机运动学模型[24],见式(1)。
2求解策略
2.1配点分布
在轨迹规划过程中,对每个时刻的控制变量优化取值会耗费大量时间,从而降低算法的效率。为了平衡计算量和效率,在轨迹规划阶段设置了配点,即将UAV飞行的时间离散为一定数量的切比雪夫点,它们是优化控制变量的时刻。切比雪夫点计算公式[25]见式(2)。
2.2粒子群算法
2.2.1公式描述
2.2.2自适应参数调整
2.2.3混沌初始化
2.3运动学模型的求解
2.3.1轨迹规划评价函数
2.3.2公式描述
2.3.3求解策略与步骤
无人机在进行轨迹规划时,面临各种参数的调试运行,仅仅求出航迹的位置信息并不能满足实际的需求。因此,若想为无人机提供更好的飞行参考指令,需结合无人机运动学模型求出各个运动学参数。具体步骤如下:
2.3.4求解流程
3仿真結果与分析
具体仿真环境:CPU为intel Corei5处理器,内存为8 GB,操作系统为windows 7 64位,主频2.1 GHz,在MATLAB R2016b环境下实现无人机轨迹规划。
3.1仿真条件设定
首先设定地形环境。为使仿真更具有真实性,将仿真环境设定为三维地形图,具体包括山峰威胁区域和雷达威胁区域,山峰用起伏的曲面表示,雷达用半球体表示。具体参数设定如表1所示。
3.2轨迹规划仿真结果与分析
3.3仿真比较
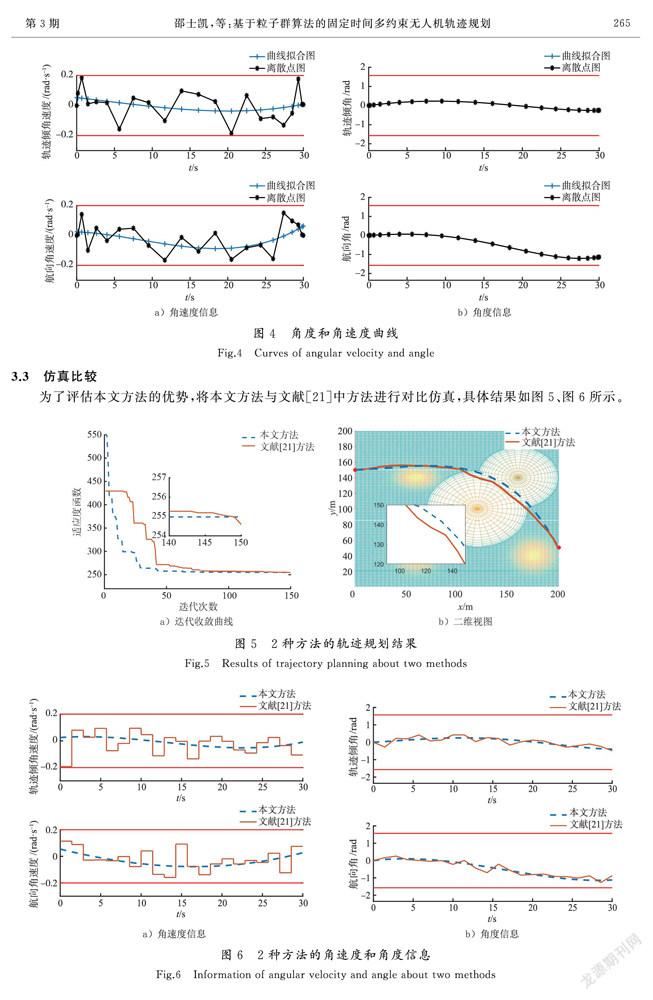
图5 a)反映了适应度函数值的变化过程,可知在同等条件下本文方法的适应度函数值会以较快的速度收敛到最优值,因此相较于文献[21]所述方法,本文方法有着更快的收敛速度。图5 b)为轨迹的俯视图,可知运用本文方法,无人机可以成功到达终点并规划出可行且平滑的轨迹,而文献[21]所述的方法产生的轨迹发生了偏折,影响到轨迹规划的效果。
为了探究轨迹偏折的原因,2种方法的角速度和角度的详细信息如图6所示。由图6 a)可知,文献[21]所述方法将时间离散等分,每个时间段的控制输入为分段常数值,而本文方法的飞行时间离散为一定数量的切比雪夫点,适用于在轨迹规划的末端时刻对多个控制变量进行处理的终端约束问题。同时,本文方法求解的控制输入为一条曲线,与文献[21]中的分段常值输入相比,本文的控制输入更接近实际情景。此外,在图6 b)中,文献[21]所述方法产生的角度连接线是一条折线,这也是直接导致轨迹波折的原因,而本文方法所求的角度值接近于一条曲线,计算数据相对稳定。因此,本文方法相对文献[21]中的方法,在算法收敛和生成平滑轨迹的问题上更具有优势。
4结语
粒子群算法在轨迹规划过程中将无人机作为质点考虑,因此求解结果只包含位置信息,求解维度比较单一,然而在实际飞行过程中,还需要涉及无人机的角度、角速度等参数信息。针对这一不足之处,本文提出通过求解无人机的运动学模型,得出各个运动学参数,使传统的仅包含位置的三维軌迹规划扩展为包含飞行时间和多种状态约束的四维轨迹规划,在提升求解维度的同时,避免了数值法计算的复杂性。
本文采用的运动学模型还较为简单,今后尚需在现有工作基础上继续进行深入研究,建立更合适的四旋翼无人机运动学模型,并探索更精确、快速的轨迹规划求解方法。
参考文献/References:
[1]GEORGE J,SUJIT P B,SOUSA J B.Search strategies for multiple UAV search and destroy missions[J].Journal of Intelligent & Robotic Systems,2011,61(1):355-367.
[2]WAI R J,PRASETIA A S.Adaptive neural network control and optimal path planning of UAV surveillance system with energy consumption prediction[J].IEEE Access,2019,7:126137-126153.
[3]TOMIC T,SCHMID K,LUTZ P,et al.Toward a fully autonomous UAV:Research platform for indoor and outdoor urban search and rescue[J].IEEE Robotics & Automation Magazine,2012,19(3):46-56.
[4]PEHLIVANOGLU Y V.A new vibrational genetic algorithm enhanced with a voronoi diagram for path planning of autonomous UAV[J].Aerospace Science and Technology,2012,16(1):47-55.
[5]何燕.基于动态加权A*算法的无人机航迹规划[J].河北科技大学学报,2018,39(4):349-355.HE Yan.UAV route planning based on improved dynamic weighted A* algorithm[J].Journal of Hebei University of Science and Techno-logy,2018,39(4):349-355.
[6]BAUMANN M,LONARD S,CROFT E A,et al.Path planning for improved visibility using a probabilistic road map[J].IEEE Transactions on Robotics,2010,26(1):195-200.
[7]KOTHARI M,POSTLETHWAITE I.A probabilistically robust path planning algorithm for UAVs using rapidly-exploring random trees[J].Journal of Intelligent & Robotic Systems,2013,71(2):231-253.
[8]甄然,甄士博,吴学礼.一种基于人工势场的无人机航迹规划算法[J].河北科技大学学报,2017,38(3):278-284.ZHEN Ran,ZHEN Shibo,WU Xueli.An improved route planning algorithm for unmanned aerial vehicle based on artificial potential field[J].Journal of Hebei University of Science and Technology,2017,38(3):278-284.
[9]MA Haiping,SHEN Shigen,YU Mei,et al.Multi-population techniques in nature inspired optimization algorithms:A comprehensive survey[J].Swarm and Evolutionary Computation,2019,44:365-387.
[10]赵新秋,段思雨,马学敏.基于阈值搜索的多目标人工蜂群算法[J].控制与决策,2020,35(8):1793-1802.ZHAO Xinqiu,DUAN Siyu,MA Xuemin.A multi-objective artificial bee colony based on limit search strategy[J].Control and Decision,2020,35(8):1793-1802.
[11]张斌,钱正祥.基于蚁群算法的无人机航迹规划技术及研究现状[J].战术导弹技术,2012(4):58-62.ZHANG Bin,QIAN Zhengxiang.Research status of route planning of UAV based on ant colony algorithm[J].Tactical Missile Techno-logy,2012(4):58-62.
[12]FISTER I,FISTER I,YANG Xinshe,et al.A comprehensive review of firefly algorithms[J].Swarm and Evolutionary Computation,2013,13:34-46.
[13]杜云,贾慧敏,邵士凯,等.面向多目标侦察任务的无人机航线规划[J].控制与决策,2021,36(5):1191-1198.DU Yun,JIA Huimin,SHAO Shikai,et al.UAV trajectory planning for multi-target reconnaissance missions[J].Control and Decision,2021,36(5):1191-1198.
[14]SHAO Shikai,PENG Yu,HE Chenglong,et al.Efficient path planning for UAV formation via comprehensively improved particle swarm optimization[J].ISA Transactions,2020,97:415-430.
[15]LEE W,KIM D E.Adaptive approach to regulate task distribution in swarm robotic systems[J].Swarm and Evolutionary Computation,2019,44:1108-1118.
[16]KARIMI J,POURTAKDOUST S H.Optimal maneuver-based motion planning over terrain and threats using a dynamic hybrid PSO algorithm[J].Aerospace Science and Technology,2013,26(1):60-71.
[17]HUANG Chen,FEI Jiyou.UAV path planning based on particle swarm optimization with global best path competition[J].International Journal of Pattern Recognition and Artificial Intelligence,2018,32(6).DOI:10.1142/S0218001418590085.
[18]PHUNG M D,QUACH C H,DINH T H,et al.Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection[J].Automation in Construction,2017,81:25-33.
[19]王荔豪,王愛华,柯楠,等.基于Dubins曲线的高超声速飞行器路径规划[J].弹箭与制导学报,2015,35(3):41-43.WANG Lihao,WANG Aihua,KE Nan,et al.Route planning for hypersonic vehicle based on Dubins curves[J].Journal of Projectiles,Rockets,Missiles and Guidance,2015,35(3):41-43.
[20]ZHANG Limin,GAO Haitao,CHEN Zengqiang,et al.Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method[J].Nonlinear Dynamics,2013,72(1):1-8.
[21]KAMEL M A,YU Xiang,ZHANG Youmin.Real-time fault-tolerant formation control of multiple WMRs based on hybrid GA-PSO algorithm[J].IEEE Transactions on Automation Science and Engineering,2021,18(3):1263-1276.
[22]WU Yu.Coordinated path planning for an unmanned aerial-aquatic vehicle (UAAV) and an autonomous underwater vehicle (AUV) in an underwater target strike mission[J].Ocean Engineering,2019,182:162-173.
[23]SHEN Chao,SHI Yang,BUCKHAM B.Integrated path planning and tracking control of an AUV:A unified receding horizon optimization approach[J].IEEE/ASME Transactions on Mechatronics,2017,22(3):1163-1173.
[24]吴宇,苏析超,崔佳鹏,等.USV&AUV水下目标协同搜索与打击航迹规划[J].控制与决策,2021,36(4):825-834.WU Yu,SU Xichao,CUI Jiapeng,et al.Coordinated path planning of USV&AUV for an underwater target[J].Control and Decision,2021,36(4):825-834.
[25]FAHROO F,ROSS I M.Direct trajectory optimization by a Chebyshev pseudospectral method[J].Journal of Guidance,Control,and Dynamics,2002,25(1):160-166.
[26]TIAN Dongping,SHI Zhongzhi.MPSO:Modified particle swarm optimization and its applications[J].Swarm and Evolutionary Computation,2018,41:49-68.
[27]YAN Yuting,ZHANG Ru,WANG Ji,et al.Modified PSO algorithms with “Request and Reset” for leak source localization using multiple robots[J].Neurocomputing,2018,292:82-90.
[28]曹詩卉,时满宏,亓迎川,等.基于混沌粒子群算法的无人机航迹规划[J].空军预警学院学报,2016,30(6):418-421.CAO Shihui,SHI Manhong,QI Yingchuan,et al.Path planning of UAV based on chaotic particle swarm optimization algorithm[J].Journal of Air Force Early Warning Academy,2016,30(6):418-421.
[29]CHAI Runqi,SAVVARIS A,TSOURDOS A.Violation learning differential evolution-based hp-adaptive pseudospectral method for trajectory optimization of space maneuver vehicle[J].IEEE Transactions on Aerospace and Electronic Systems,2017,53(4):2031-2044.

