Effect of B4C on strength coefficient, cold deformation and work hardening exponent characteristics of Mg composites

S.Suresh, M.Nvneeth Krishnn, S.C.Vettivel

a Department of Mechanical Engineering, University College of Engineering, Nagercoil, Tamilnadu, India, Pin: 629 004

bDepartment of Mechanical Engineering, Universal College of Engineering and Technology, Vallioor, Tamilnadu, India, Pin: 627 117

c Department of Mechanical Engineering, Chandigarh College of Engineering and Technology, Chandiagarh 160019, India

Abstract

Keywords: Powder metallurgy; Cold deformation; Workability; Instantaneous work hardening exponent; Workability stress exponent; Triaxial stress.

1.Introduction

The magnesium (Mg) is used in the automotive, electronics, and aerospace sectors.It is due to their greater strength to weight proportion, low densities, better mechanical properties, more stiffness and specific strength, better thermal conductivity, and vibration-damping capacity [1–3].Mg related metal matrix composites have wide applications in automotive, medical, and aerospace areas since Mg is the lightest metal which creates greater specific strength MMCs [4].Mg is applied in biomedical, automotive, consumer electronics, sports, gearboxes, and helicopter transmission casings[5].However, the Mg application is limited because of their quick strength loss with increasing temperature, low creep resistance at elevated temperatures, and low elastic modulus[6–8].Hence,proper reinforcement needed to improve the Mg properties [4].

Ceramic particle added Mg composites possess applications in the aerospace and automotive sector because of their lesser weight and greater specific strength [9].Boron carbide(B4C) is an essential material for several reasons.It has less density (2.51g/cm3), good chemical resistance, and very hard[4].The inclusion of B4C in the Mg matrix enhances the flexural strength and interfacial bonding strength of composite[7,10].In terms of density, Mg and B4C possess 1.74g /cm3and 2.52g/cm3respectively.The produced Mg/B4C composite have an additional lesser weight and approximately 2g/cm3density [3].The B4C has important applications in airborne transport vehicles, land borne and light armor due to its high hardness, less density, and elevated modulus [11].

The powder metallurgy (P/M), stir and squeeze casting routes are the typical fabricating methods for processing the Mg-based composites [9].The P/M method offers more benefits over these techniques for producing the composite.P/M needs less temperature for fabrication and increases better homogeneity of particle distribution, especially greater volume fraction obtained for a ceramic particle but these are very tough to attain by other routes [6,12].Usually, using a suitable blending and sintering process can succeed in porous-free and fine microstructure [13-15].Balakrishnan et al.[16]experimented to make AZ31/TiC magnesium-based composites utilizing FSP and investigated the microstructure using SEM.Four distinct(0,6,12,and 18%)volume fractions of TiC particles were taken.The SEM examination specified that TiC particles were uniformly dispersed in the Mg matrix without any clusters formation.There was no interfacial reaction among the Mg and TiC particles.

Workability is a deformation measurement that the P/M specimen can resist before crack takes place during the upsetting or forming process [17,18].The workability measures the specimen capability against the crack formation and permanent deformation due to the internally developed stresses[19,20].To find the workability and load-carrying capability of the specimen, the deformation experiment was conducted by giving a compressive incremental load [21].Szczepanik et al.established that the specimen with the more relative density and less aspect proportion had better formability [22].Reducing the composites aspect ratio provides superior formability stress index rate due to the more densification.The relative density (R) of preform enhances monotonically with load [23].The hot deformation performance of the ZK21 alloy was examined by Wu et al.[24].They concluded that the workability of ZK21 alloy improved with the increase of deformation and strain rate at around 10 s-1strain rate and 250–400 °C temperature was feasible and desirable for ZK21 alloy.

Yan et al.[25]examined the compression workability behavior of AZ61-SiCp magnesium-based composites.The AZ61- SiCp composites flow stress enhances with the increment of SiC volume fractions.The semi-solid AZ61-SiCp composites flow stress is responsive to the rate of strain and heat.Flow stress enhances with lower temperatures and a superior rate of strain.The factor which describes the work hardening performance of the specimen is called work hardening exponent.This is caused by the permanent decomposition of the specimen under room temperature [26].Work hardening performance of Al–ZrB2preform is analyzed by Yadav Kaku et al.[27]and found that at static strain hardening states, the value of strain reduces with the ZrB2particle.The consequences of work hardening and workability factors such as various stresses, relative density, instantaneous coefficient of strength and instantaneous work hardening exponent under triaxial stress condition were studied by Selvakumar et al.[18]and established that work hardening and workability factors enhance with increasing of reinforcement particle because of the relative density growth.Less aspect proportion specimen permits identical density compared with greater density specimen, as a result of the fast transmission of a load.

It could be perceived from the literature that not much study reported on the workability and work hardening effect of Mg-B4C composite so far.Hence this examination intends to explore the work hardening and workability effects of Mg specimen and Mg-B4C (5–15%) composites using cold deformation experiments.In this present analysis, Mg specimen and Mg-(5–15%)B4C composites are fabricated using P/M techniques and conduct characterization such as SEM and EDS with elemental mapping.The consequences of workability stress exponent parameter, relative density, instantaneous work hardening exponent, instantaneous coefficient of strength, coefficient of strength, strain hardening exponent,several stresses,and stress proportion factors on Mg specimen and Mg-(5–15%)B4C composites are performed, recognized,recorded and reported.

2.Experimental details

2.1.Materials and microstructures

Mg and B4C micron powders were chosen to analyze the characterization, work hardening, and workability performance of Mg and Mg-B4C composites.The Mg powder with 74μm sizes and B4C powder with 44μm sizes were utilized for this exploration.The Mg and B4C powders with 99.95%and 99% purity were used.SEM is used for analyzing and deciphering the microstructures of the materials.The SEM investigation of the obtained Mg and B4C particles has been performed and is displayed in Fig.1 (a-b).Mg comprises of relatively splendid characterization.Fig.1a shows that Mg particles are deformed ellipsoidal and spherical shape.It has a particle size limits between 40 to 90μm and rough surfaces with uneven structure.Fig.1b identifies that B4C particles are in the polygonal structure.

2.2.Specimen preparation

2.2.1.Blending of powders

The Mg and B4C powders were pulverized exclusively and mixed at various weight percentages utilizing an appropriate ball mill with 10mm tungsten carbide balls.The mass ratio between the ball and the powder was 20: 1.The distinctive weight percentage (5–15%) of B4C powders were milled and mixed with Mg at 200rpm speed and for 2 hours.The Mg and B4C particles were mixed based on weight percentages due to simple calculation.

2.2.2.Compaction

Compaction is the method toward compressing of metallic powder in the die through greater loads.The cold compaction was performed with 1MN maximum capacity universal test machine and suitable die-punch.The cold compaction procedure was carried out by pouring the mixing particles inside the hole of a die and then giving 500MPa uniaxial compressive loads gradually.The cold compaction experiments wereconducted as per the Metal powder Industries Federation: 42(MPIF: 42) standard [28].To lessen the friction between die and punch, the graphite powder was utilized as a lubricant on their contact surfaces before the compaction process.After adequate uniaxial compressive loading was given, the green compacted specimens were taken safely from the die.Similarly, Mg - (5–15%) B4C specimens were fabricated at room temperature conditions.Fig.2 signifies the compaction process performed by the UTM.

Fig.1..SEM image (a) Mg powder (b) B4C powders.

Fig.2.Compaction process using UTM.

2.2.3.Sintering

The samples obtained at the cold compaction process were sintered to 590 °C by electric muffle furnace for 2h.The problem of Mg composites during sintering is combustion and oxidation.Both problems can be rectified using charcoal and coating of alumina-colloidal graphite mixture on the samples.The compacted sample was preserved in an argon atmosphere to evade oxidation in the time of sintering.After the alumina-colloidal graphite mixture was coated on the samples and dried to room temperature, they undergo to the sintering process.Charcoal was used to protect the specimens by purifying and eliminating oxygen contamination in the furnace during heating.During sintering, charcoal emits CO2at very minimum temperatures nearby the specimen.The CO2surrounding the specimens are protects them from burning even at high temperatures.The sample was cooled in the furnace until it reached room temperature.The sintering was properly monitored throughout the process.Afterward, the sintering was accomplished, the sample was cooled within the electric muffle furnace to ambient temperature and the sintered specimens are given in Fig.3.

2.3.Characterization of composites

Before conducting characterization studies on the Mg-B4C specimen, they were sliced to the necessary height by the EDM wire cutting machine, and then the surface was polished.The prepared specimen was not collaborating for morphology study due to its rough surfaces.Polishing and etching are the important primary processes for the characterization study.Polishing was performed in two stages specifically primary and secondary process in which primary polishing includes 600 grits emery paper and secondary polishing was carried out using disc polishing machine with diamond polishing paste.Then the polished surfaces of the specimen were subjected to an etching process using an acetic glycol according to the metallographic approach.Afterward,the etched surface was dried in atmospheric air and utilized for morphological study.

2.3.1.SEM microstructure

SEM was studied to confirm the distribution of B4C grains in the Mg.The SEM study confirms that the B4C reinforce-ment particles are dispersed well with magnesium.The SEM image of Mg-B4C composites with dissimilar B4C wt.% (0,5, 10 and 15%) are given in Fig.4 (a-d).The dark area in Fig.4 represents Mg and the brightest part is B4C.This ensures that the B4C particles are well mixed and dispersed with Mg.The micro constituents of Mg specimen are in the form of irregular, wafer, and platelet structure and it has a very strong bond between them.The different hexagonal shapes and sizes are found in Mg- B4C composite.This is due to the accumulation and combined bonding of Mg and B4C particles.The Mg and B4C particles make a strong chemical bond among them and develop a solid structure.No difference between the Mg and B4C elements in the Mg-B4C composites was observed in the SEM micrograph.This is because fine B4C particles are well distributed in the Mg matrix.

Fig.3.Sintered specimens.(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig.4.SEM image (a) Mg specimen (b) Mg-5B4C (c) Mg-10B4C (d) Mg- 15B4C.

2.3.2.Energy dispersive spectroscopy analysis

EDS is an analytic method used to examine the elemental characterization or elemental composition of samples.In this present analysis, the EDS spectrum was used to con-firm the elements present in the Mg specimen and Mg-(5–15%)B4C composites.Fig.5 display the elemental map results of Mg-B4C composites.The elemental image has three colors namely Green, Blue, and Yellow.The color of Mg,boron, and carbon looks green, blue, and yellow respectively.The existence and distribution of Mg, B, and C particles are confirmed through this elemental map analysis.The green component is higher than the blue and yellow components.Since more percentage of Mg metal presents in the Mg-B4C composites.Hence, the remaining two colors are less.It is observed that the B4C particles were uniformly spread with the Mg matrix.It was affirmed that no oxide being in the sintered Mg-B4C composite is observed.This is an outcome of better chemical bonding amongst the Mg and B4C particles.However, few agglomerations of carbon can be noticed in grain boundaries.That is, it is clear that Mg and B4C particles are distributed with very fewer agglomerations at the grain boundaries.

Fig.5.Elements presents in Mg-B4C composites (a) magnesium (b) boron (c) carbon.

The Mg and B4C particles peaks and elemental composition were affirmed by EDS investigation and are given in Fig.6.EDS image of Mg-B4C composites displays the intense signals of Mg, carbon, and boron at 1.22 Kev, 0.27 Kev, and 0.18 Kev values.Mg has a greater peak than boron and carbon due to the more weight percentage.The level of carbon and boron peaks increases with the increase of B4C inclusion.The received results are concurrence with the outcomes already found in [29].

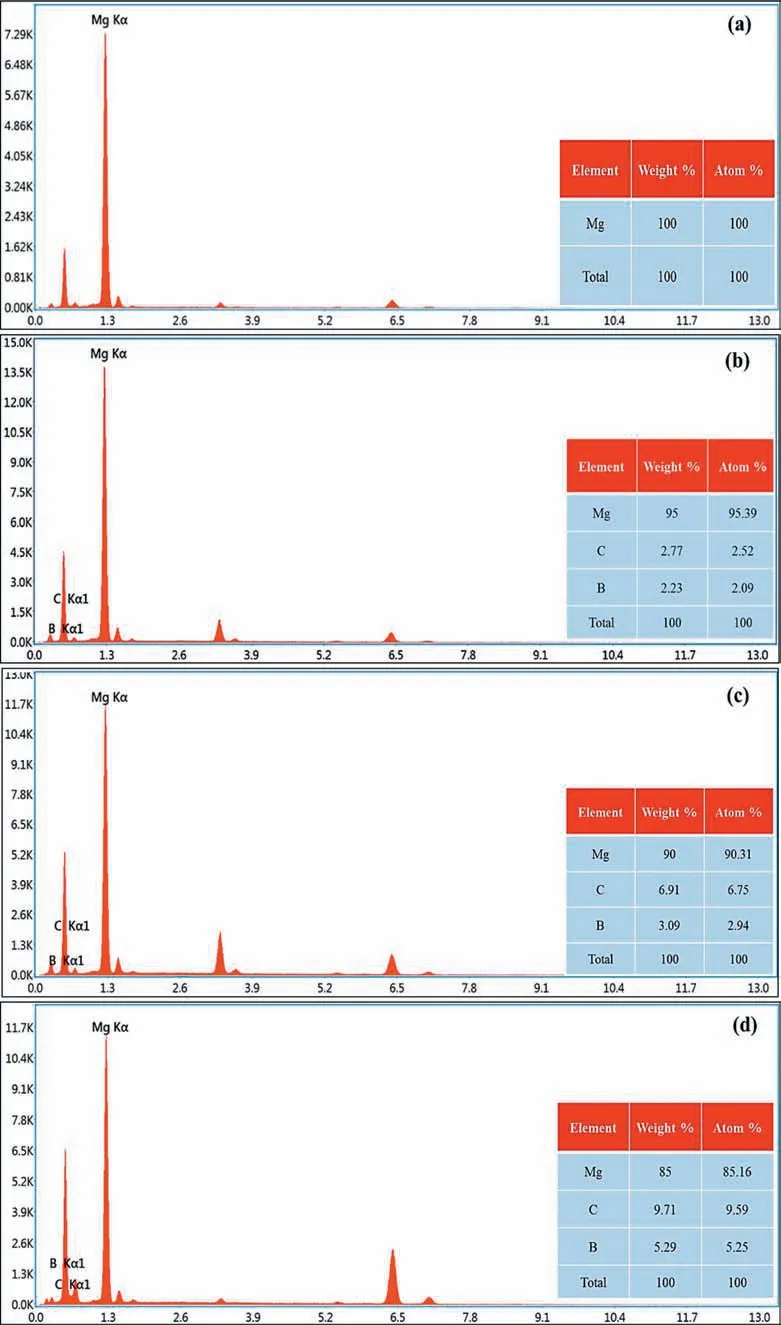
Fig.6.EDS image (a) Mg specimen (b) Mg-5B4C (c) Mg-10B4C (d) Mg-15B4C.

2.3.3.X-ray diffraction investigation

The crystal configuration and phase identification of Mg-B4C composites were measured using XRD analysis.The 1.54060wavelength X-rays were made using CuKαradiation and used to create the particle diffraction patterns.XRD investigation was performed under test conditions of 3–90oscan ranges, 2θangle, 0.02ostep width and 6s time duration.The Debye-Scherrer technique utilized to compute the crystalline extent of the elements in the composites.The Debye-Scherrer formula used for crystalline size measurement was mentioned in Eq.(1).

Where, D – the size of crystal;λ– wavelength;β– width of peak andθ– the angle of diffraction.

The XRD results for the prepared Mg-B4C composite are given in Fig.7 (a-c).All the specimen display the broad diffraction peaks, which can be indexed to the Mg and B4C structures.The Mg and B4C peaks were diagnosed in the XRD image of the Mg-B4C composites.The crystalline extent of the Mg-5%B4C, Mg-10%B4C, and Mg-15%B4C composites evaluated from the Debye-Scherrer expression was 64.097nm, 46.339nm, and 36.410nm, respectively.It can be found that the Mg diffraction peaks have the relative intensity rate corresponding to the 2θangle 38.94o, 45.19o, 65.67oof(1 1 1), (2 1 0), (3 1 0) and it was seen to be the diffraction peaks of B4C has the relative intensity rate corresponding to the 2θangle 36.11o, 65.19o, 82.74oof (1 1 1), (2 2 0),(3 2 1).

2.4.Experimentation

2.4.1.Cold deformation experiment

The cold deformation experiment was conducted to determine the workability performance of the Mg-B4C composites with differences in B4C content (0, 5, 10 & 15%).Before conducting cold deformation tests, the primary density (ρo),primary height (ho), theoretical density (ρth), and primary diameter (Do) were measured.The initial density (ρo) of the specimen was measured utilizing the Archimedes principle.This process was conducted by applying a compressed load of 0.01 MN to all samples through a 1MN capable UTM machine.Measure the specimen density (ρf), specimen height(hf), contact bottom diameter (DCB), the diameter of bulging(Db), and contact top diameter (DCT) after the deformation.The contact diameter (DC) of the specimen was calculated using the value of DCTand DCB.The relative density of the specimen was calculated from the ratio of their density after deformation (ρf) and theoretical density (ρth).The deformation effect in the specimen before and after the upsetting process was illustrated in Fig.8 (a-b) as mentioned by Kumar et al.[30].As mentioned above, the compressive load was given progressively for every specimen until the visible initial crack takes place in the specimen.The primary crack occurred in the composites during the upsetting process was displayed in Fig.9.The composite workability performance is decided through the stress exponent formability parameter(βσ) and it depends on the triaxial effective and hydrostatic(σeffandσm) stresses.

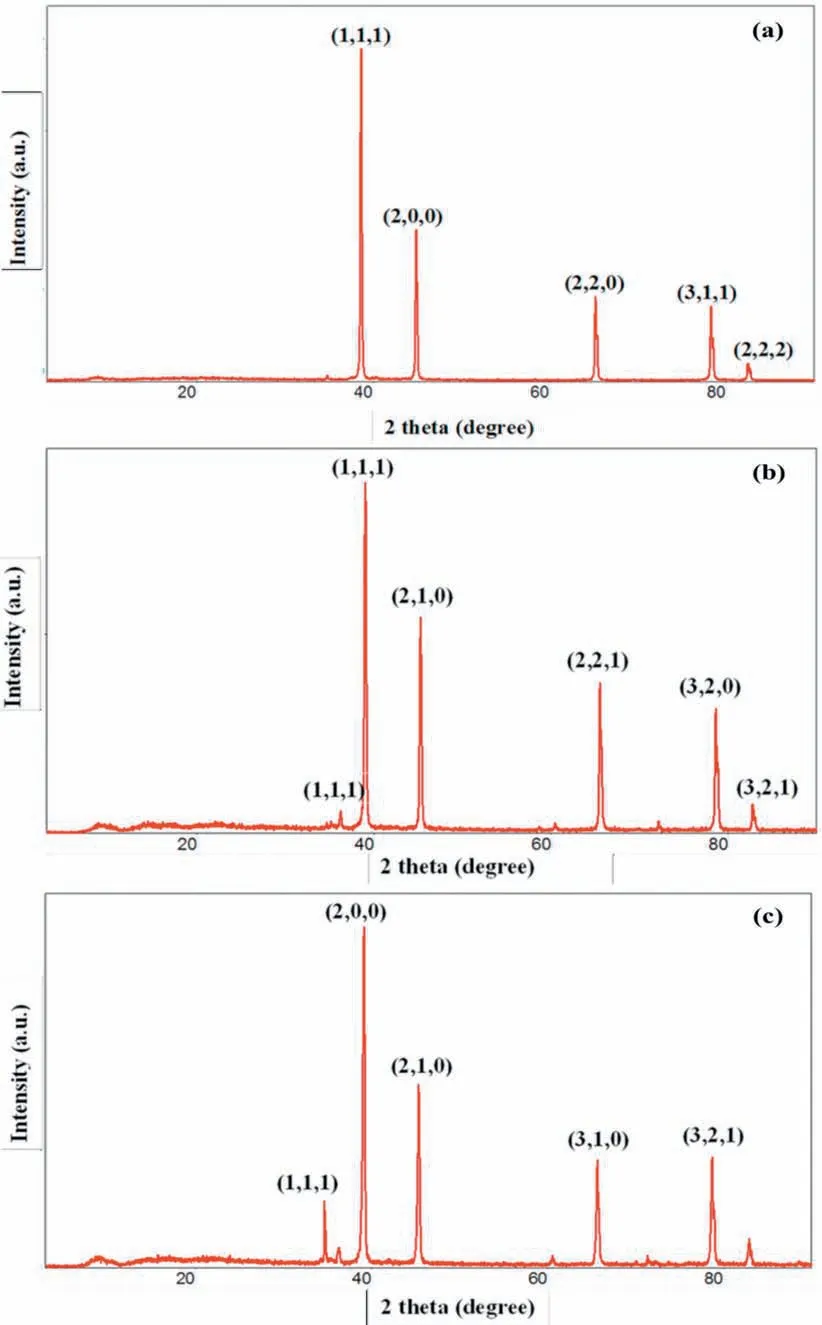
Fig.7.XRD analysis of the composites (a) Mg-5B4C (b) Mg-10B4C (c) Mg-15B4C.

Fig.8.Cold deformation process(a)before deformation(b)after deformation(Kumar et al., 2011).

2.4.2.Work hardening exponent and coefficient of strength

Work hardening index (n) and coefficient of strength (k)are manually determined through the log sheet.At first, the curve was drawn amongst the axial true stress (σz) vs.axial true strain(εz)on vertical and horizontal axis correspondingly.Thereafter a tangent is drawn to the curvature.It extended till the axial true strain value of one.Currently measured the vertical axis value and that same were equal to the coefficient of strength (k).The slope of the plotted curvature was computed by way of taking the ratio of perpendicular span to the horizontal span and the same was equal to the work hardening index (n).

3.Theoretical exploration

3.1.Density evaluation

The relative and theoretical densities (ρth& R), the density of specimen before and after deformation (ρo&ρf)are vital parameters for determining the formability of Mg-B4C composites whereinρfandρoare measured through the Archimedes principle following the standard of ASTM:B962–13 [31].The composition rule was used to determine the theoretical density (ρth) as stated in [32].

The proportion of density of specimen after distortion to the theoretical density is called relative density.Usingρfandρthvalue, the relative density (R) was calculated as given in Eq.(2).

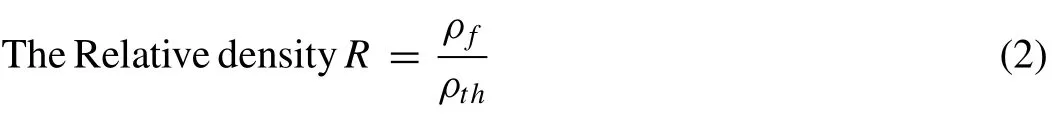
Where,ρfspecimen density after distortion andρththeoretical density.

3.2.Triaxial stress state

The Mg-B4C composites undergo volumetric deformation during the cold upsetting process.This is since the mutually perpendicular principal or normal stresses act on the three dimensions of the specimens.Generally, in the uniaxial stress state condition principal stress acts on only one dimension and is zero in the other two directions.Due to the deformation shape, in the biaxial stress condition, the principal stresses act only in two dimensions but it is zero in other directions.Uniaxial and biaxial stress states apply only to uniaxial and biaxial compressions respectively as they affect the actual flow property of the composites.Hence,they are not acceptable for the cold deformation process.Therefore, triaxial stress condition is optimal for obtaining an actual flow property of the composites [33].

The contact diameter (DC) is a basic requirement to calculate the area of contact (AC) after distortion and is given in Eq.(3).

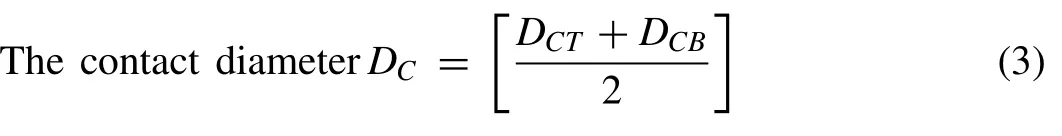
Where DCTand DCBare the contact top and base diameter after distortion respectively.

The area of contact was evaluated from Eq.(4).

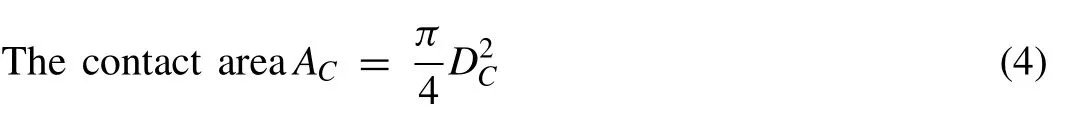
3.2.1.Triaxial stresses

Effective stress (σeff), axial stress (σz), mean stress (σm),and hoop stress (σθ) are used to evaluate the workability of composites [34].The stress produces the deformation by the axial load is called axial true stress(σz).Theσzis determined to utilize the following Eq.(5).

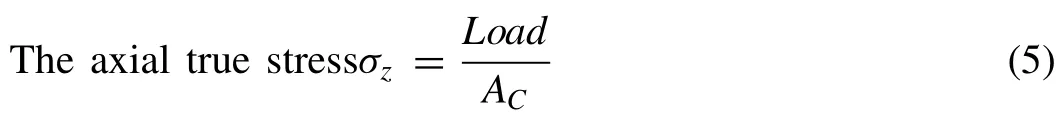
Poisson proportion (α) is the most significant and necessary factor to estimate the circumferential stress (σθ).It isthe proportion of increment in circumferential strain and axial strain [35].Before evaluating the hoop stress (σθ), the Poisson ratio (α) is calculated by Eq.(6) [17].

Fig.9.Before and after deformation of specimen during upsetting process (a) Mg (b) Mg-5B4C (c) Mg-10B4C (d) Mg-15B4C.

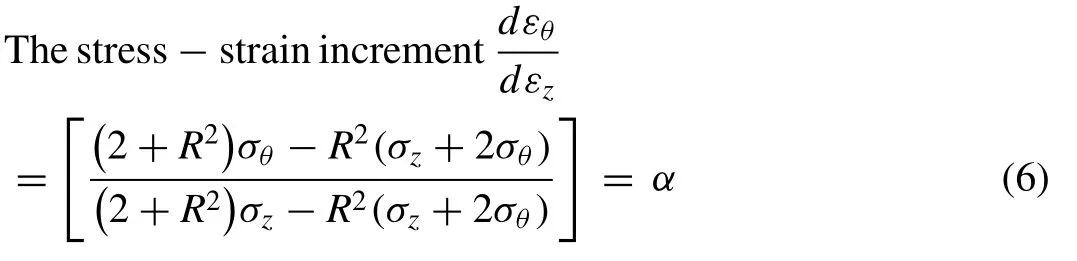
Where, R relative density;σzaxial true stress;σθ– circumferential stress andαPoisson proportion.

The stress performing on the perimeter of the specimen is called hoop stress (σθ).In particular, the hoop stress is superior to axial true stress (σz).The formula for the circumferential stress (σθ) obtained from the mathematical relationship of Poisson proportion (α) is given in Eq.(7).

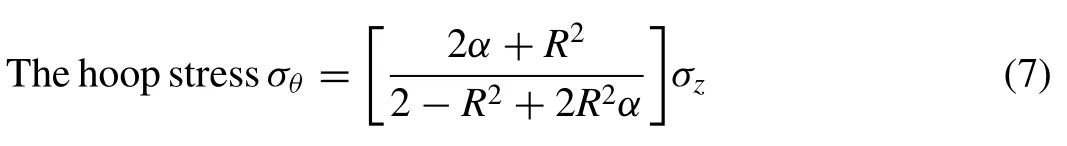
Hydrostatic stress (σm) is the median of three principal or normal stresses.The mean stress expression for the process of cylindrical upsetting or forming is mentioned in Eq.(8).

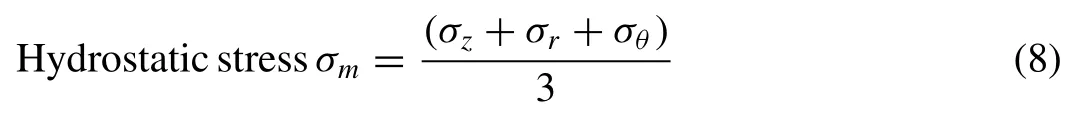
In general, true axial stress (σz) has a compressive nature but hoop (σθ) and radial stresses (σr) have a tensile nature.As stated by Narayanaswamy et al.[17]in the state of triaxial condition, radial stress (σr) is equal to hoop stress (σθ).Hence, after simplifying the above Eq.8, they specified in Eq.(9).

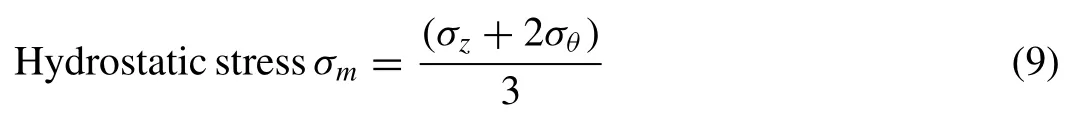
Effective stress (σeff) is the stress required to achieve an initial critical state from a yielding position.The effective stress formula for the cylindrical upsetting or forming phenomenon as mentioned by Sumathi et al.[36]is given in Eq.(10) below.

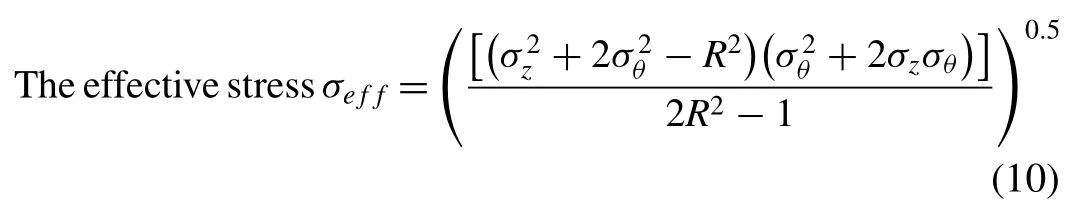
Whereσz– axial true stress andσθ– circumferential stress.

3.2.2.Triaxial strain

The axial true strain (εZ), conventional circumferential strain (ε′θ) and true circumferential strain (εθ) are assuming a significant part in workability studies.All strains were computed according to the same standard adopted in [36].

Measuring the deformation in the specimen due to axial stress is called real axial strain.True axial strain (εz) for the cylindrical upsetting or forming process is calculated using Eq.(11) as mentioned below:

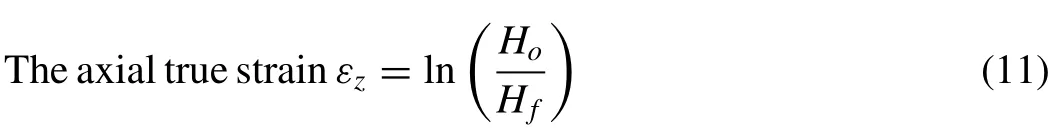
The true circumferential strain is the diametric strain.The ratio of the difference in circumference to the original circumference of the sample as a result of the circumferential stress is known as true circumferential strain (εθ).Theεθfor the cylindrical upsetting or forming process is given in the following Eq.(12) as stated in [37].

3.2.3.Stress exponent formability parameter (βσ)

The specimen capacity to resist the distortion contrary to the applied load is known as formability.The effective and mean stresses cause the major effects in stress exponent formability parameter (βσ).As reported in [38], the formula for calculating the stress index formability factor is given in Eq.(14).

As Selvakumar et al.specified in [18]:

Utilizing the Eq.(15) and (16), exponent of instantaneous work hardening (ni) and instantaneous coefficient of strength(ki)of Mg-B4C composites can be computed from the respective triaxial stress and strain values.

4.Results and discussion

4.1.Consequences of various stresses depending on the axial true strain

The consequences of various stresses like effective, mean,circumferential and axial true stresses (σeff,σm,σθ,andσz)depending on axial true strain (εz) for the Mg-B4C composite with the difference in B4C content (0, 5, 10 & 15%) are displayed in Fig.10 (a–d).Except for the true axial stress,the curvatures of all other stresses are present above the horizontal axis.The axial true stress alone is below the axis because of its compressive nature.In the beginning, every stress slowly enhances with increasing an axial true strain because of opposition to the distortion by every specimen.Thereafter,curvature continuously enhances till the primary crack occurred in the composite due to increasing relative density (R)and an increase of load distribution.The outcome displaysthat,σz(axial true stress) value was larger compared with circumferential stress (σθ).It was recognized thatσmandσeffpossess the least and higher value respectively due to better density.The result shows that superior stresses and axial true strain are attained for Mg-15%B4C composite.The reason was that added B4C content reduces the pore extent and enhances the relative density and as well of its perfect dispersion in the Mg.Therefore Mg-15%B4C composite has necessary additional loads to create the distortion.The highest value of various stresses for Mg-(0–15%) B4C composite and comparison with previous reports were indicated in Table 1.The results have good agreement with [18,26,33].

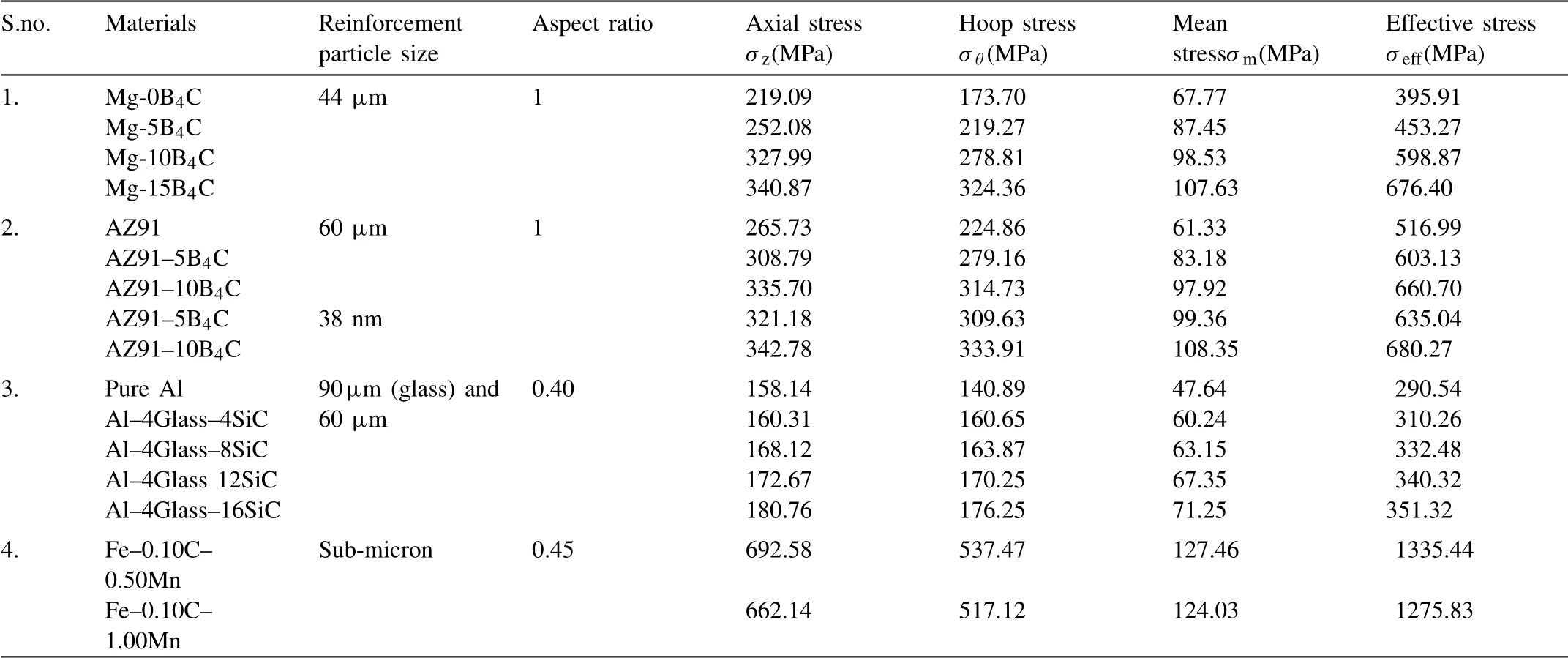
Table 1The highest value of various stresses and comparison with previous reports [26,33,41].

Fig.10.Consequences of various stresses depending on the axial true strain (a) Mg specimen [32](b) Mg-5% B4C composite [32](c) Mg-10% B4C composite(d) Mg-15% B4C composite.

4.2.Consequences of axial stress (σz) depending on the relative density (R)

The consequences of axial true stresses depending on relative density for the Mg-B4C composite with a difference in B4C content (0, 5, 10 & 15%) are displayed in Fig.11a.In the beginning, the relative density was enhanced more yet theσz(axial stress) enhanced very minimum at the start because of the opposition against the deformation for every specimen.The closure pores in the composites rapidly conquer the space while the deformation increases.Thereafter, relative density is gradually enhanced because the closure pores in the composites conquer the space was reduced, however axial true stress enhanced to some extent than the initial period.Similarly, both axial stress (σz) and relative density (R) constantly enhanced all over the period until primary crack occurred in the composites.The result shows that superior relative density and axial true stress are attained for Mg-15%B4C composite.It is due to the decrease of porosity by the particle of B4C and the good distribution of B4C particle in Mg-15%B4C composite.Therefore Mg-15%B4C composite has necessary additional axial true stresses to create the distortion.The result has great concurrence with [30,36].

4.3.Consequences of the formability stress index(βσ)depending on the relative density

The consequences of stress exponent formability parameter(βσ) depending on relative density for the Mg-B4C composite with a difference in B4C content (0, 5, 10 & 15%) are displayed in Fig.11b.Initially, relative density and stress exponent formability is enhanced due to improvement in mean stress (σm) and the better closure of pore for all the composites.Usually, at the beginning of distortion, theσmis greater compared withσeff.The curvature of Mg-15%B4C composite enhanced straight up in the till it reaches the R-value of 0.95.Thereafter,in the rest of the portionσeffenhanced andσmdecreased due to better closing of the pore.Theβσ(formability stress index) is consistently enhanced by increasing the relative density.Relative density and workability are directly proportionate to one another.Relative density and workability of composites enhance while increasing the inclusion of B4C reinforcements.Indeed, workability experiments increasing the R-value,by enhancing the density of specimen after distortion(ρf)because closure pores in the composites reduce the space.The outcome displays that Mg-15%B4C composite possesses a greater R-value of 0.9861 compared with other composites.The Mg-15%B4C composite has a greater R (relative density) value and workability stress index (βσ) compared with the Mg-(0–10%)B4C composites because of its greater mean stress value.The highest value of stress exponent formability parameter for Mg-(5–15%) B4C composite and comparison with previous reports are listed in Table 4.The results show good agreement with the findings [26,30,35].

4.4.Consequences of relative density (R) depending on the axial strain (εz)

The consequences of relative density depending on axial true strain for the Mg-B4C composite with a difference in B4Ccontent (0, 5, 10 & 15%) are displayed in Fig.12a.Quadratic polynomial parabolic curve fitting method used to draw the graph.Table 3 mention the coefficient of regression (R2) and quadratic equations of Mg-B4C composites and it as well displayed that the Mg-15%B4C composite possesses superiorR2(0.952) value.On account of increasing the B4C additionε2ZandεZthe coefficient in the equation reduces and the constant value increases.TheR(relative density) value becomes greater as a consequence of increasing theεz(axial strain)value for all the composites.In the beginning, R-value enhances with the increase ofεz.Subsequently,R-value increasing consistently with an increment ofεz.Fig.12a confirmed that Mg-15%B4C composite possesses superior R-value compared with other composites because the closure pores in the composites reduce the space by B4C content.Table 2 shows the highest value of relative density for the Mg-B4C composites and comparison with previous reports.These findings are well agreed with earlier studies [18,26].

Table 2The highest value of relative density for composites and comparison with previous reports [26,41].

Table 3The acquired curvature fitting outcomes relative density versus axial true strain.

Fig.11.(a) Consequences of axial stress depending on the relative density for Mg-B4C composite with difference in B4C content (0, 5, 10 & 15%) (b)Consequences of formability stress index depending on the relative density for Mg-B4C composite with difference in B4C content (0, 5, 10 & 15%).

4.5.Consequences of stress exponent formability parameter(βσ) depending on axial true strain (εz)

The consequences of stress exponent formability parameter depending on axial true strain for the Mg-B4C composite with a difference in B4C content (0, 5, 10 & 15%) are displayed in Fig.12b.The graph was drawn using a quadratic polynomial parabolic curvature fitting method.Table 5 mention the coefficient of regression (R2) and quadratic equations of Mg-B4C composites and it as well displayed that the constant value inthe equation enhances andε2zandεzcoefficient reduces with increasing of B4C addition.The greater R2value (0.992) was attained for Mg-15%B4C composite compared with the other composites.The stress exponent formability parameter and axial true strain were acquired using Eq.(11) and (14).The stress exponent formability parameter(βσ)enhancing more as increasing ofεz(axial strain) for every specimen.The Mg-15% B4C composite contains superiorβσvalue compared with Mg-(0–10%)B4C composites for a respective increase inεzvalue due to the increasing ofσm(mean stress) and better closure pore during the cold upsetting.Maximumβσvalue acquired for the Mg-B4C composite with difference in B4C content (0, 5, 10 & 15%) are 0.3890, 0.4450, 0.4624 and 0.4804 respectively.The result has great concurrence with[19,30].

Table 4The highest value of stress exponent formability parameter for composites and comparison with previous reports [26,30,35,41].

Table 5The acquired curvature fitting outcomes- stress exponent formability parameter (βσ) versus axial true strain (εz).

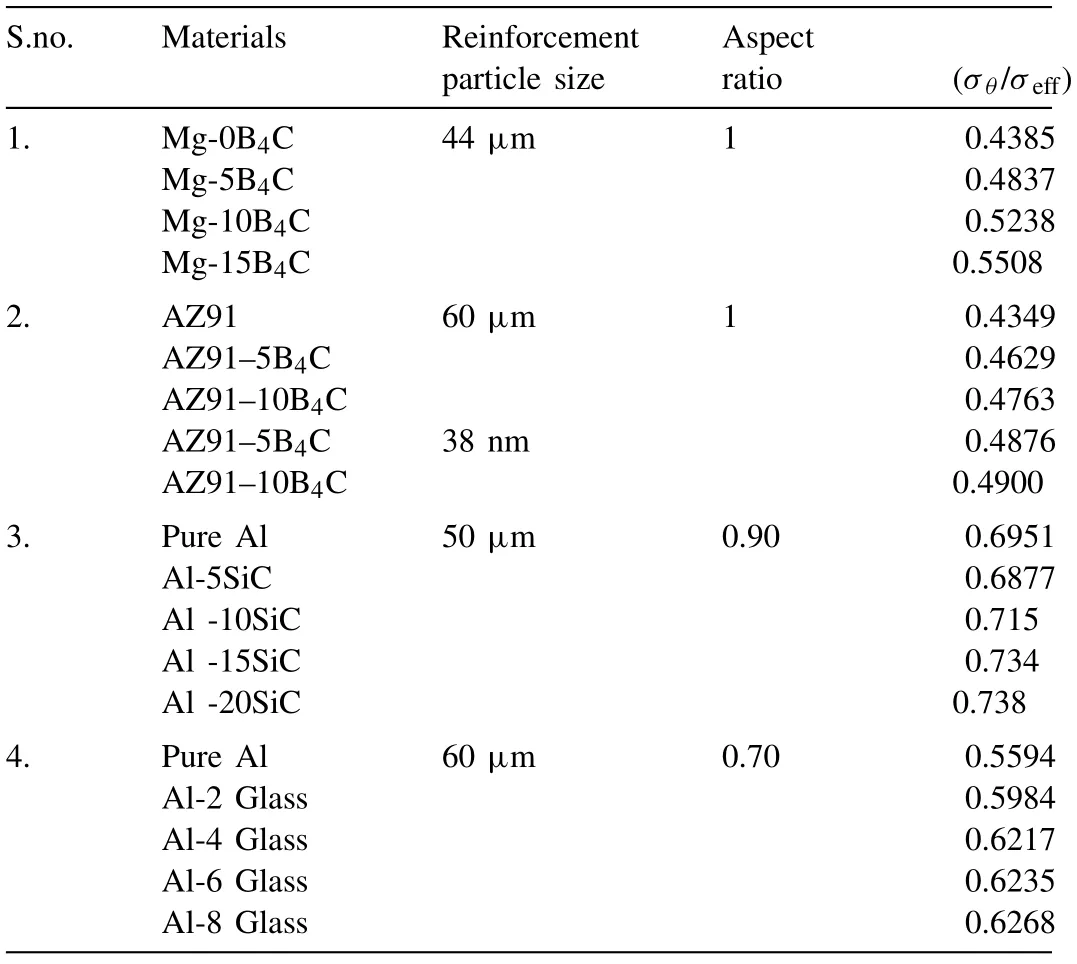
Table 6Highest value of stress proportion factor (σθ/σeff) for the composites and comparison with previous reports [30,35,41].

Table 7The attained curvature fitting outcomes-stress proportion factor (σθ/σeff) versus relative density.

Fig.12.(a) Consequences of relative density depending on axial true strain for the Mg-B4C composite with the difference in B4C content (0, 5, 10 & 15%)(b) Consequences of stress exponent formability factor depending on axial true strain for the Mg-B4C composite with the difference in B4C content (0, 5, 10& 15%).

4.6.Consequences of stress proportion factors depending on relative density

Theσm/σeff&σθ/σeffare the two stress proportion parameters used for present exploration.The consequences ofσθ/σeffstress proportion parameter depending on relative density for the Mg-B4C composite with the difference in B4C content (0, 5, 10 & 15%) are given in Fig.13a.The consequences ofσm/σeffstress proportion parameter depending on relative density for the Mg-B4C composite with the difference in B4C content (0, 5, 10 & 15%) are displayed in Fig.13b.Table 6 indicates the highest value of stress proportion factor (σθ/σeff) for the Mg-B4C composites and comparison with previous reports.The graph was drawn using a quadratic polynomial parabolic curvature fitting method.Table 7 mentions the curvature fitting outcomes ofσθ/σeffdepending on R.Table 8 indicates curvature fitting outcomes ofσm/σeffdepending on R.

The outcome displays that the superior value of R2(coefficient of regression) attained for Mg-15%B4C composite.Particularly, Table 8 confirmed that Mg-15% B4C composite possesses the R2(coefficient of regression) value closer to one.It is well displayed that the constant value in the equation enhances and R2and R coefficient reduces with increasing of B4C addition because of the higher relative density.Bothσθ/σeff&σm/σeffrises to the enhancing of R (relative density) for all the composites because of the increase in circumferential and mean stresses.Maximumσθ/σeff&σm/σeff(stress proportion parameters) acquired for higher relative density composite.In the beginning,σθ/σeff&σm/σeff(stress ratio factors) increased gradually due to its low value of relative density and greater opposition against the deformation of the composites.Subsequently, bulging occurred in the specimen due to the increase of relative density, mean, and circumferential stresses.It is caused due to the closure pores in the composites and hence space was reduced.Bothσθ/σeff&σm/σeffare eventually enhanced more than the preceding level due to its increasing R-value.So it causes the creation of primary crack in the composite owing to the damaging of pores inside the specimen.The attained R-value for Mg-15%B4C composite was greater than other specimens, since,porosity is reduced by the increasing of B4C content.The result has good agreement with [18,30,35].

Table 8The acquired curvature fitting outcomes-stress proportion factors (σm/σeff)versus relative density.

4.7.Consequences of an instantaneous exponent of work hardening (ni) depending on axial true strain (εz)

The consequences of an instantaneous exponent of work hardening (ni) depending on axial true strain for the Mg-B4C composite with the difference in B4C content (0, 5, 10 &15%) are given in Fig.14a.It shows three stages [18].The instantaneous exponent of work hardening increased vertically with a slight growth of axial true strain at the beginning owing to the opposition against the deformation of the Mg matrix.Thereafter, the magnesium runs inside the pores by overcoming the opposition of the specimen.At this instant, the work geometry hardening is a superior extent than the insignificant extent of work magnesium hardening.Hence the nivalue reduced while growing of axial true strain.

At last, work magnesium hardening enhances until the formation of primary crack than work geometry hardening.Consequently, the nivalue enhanced for the less growth in axial true strain.At this instant, the work geometry harden-ing is small.The highest value of instantaneous exponent of work hardening for the Mg-B4C composites and comparison with previous reports are shown in Table 9.These curves outcomes are in better concurrence with the findings in [26,39].Table 9 exposed that Mg-15%B4C composite possesses the highest nivalue and lesser for Mg specimen.

Table 9Highest value of instantaneous coefficient of strength and instantaneous exponent of work hardening for the composites and comparison with previous reports [26].

Fig.13.(a) Consequences of σθ/σeff depending on relative density for the Mg-B4C composite with difference in B4C content (0, 5, 10 & 15%) (b)Consequences of σm/σeff depending on relative density for the Mg-B4C composite with difference in B4C content (0, 5, 10 & 15%).

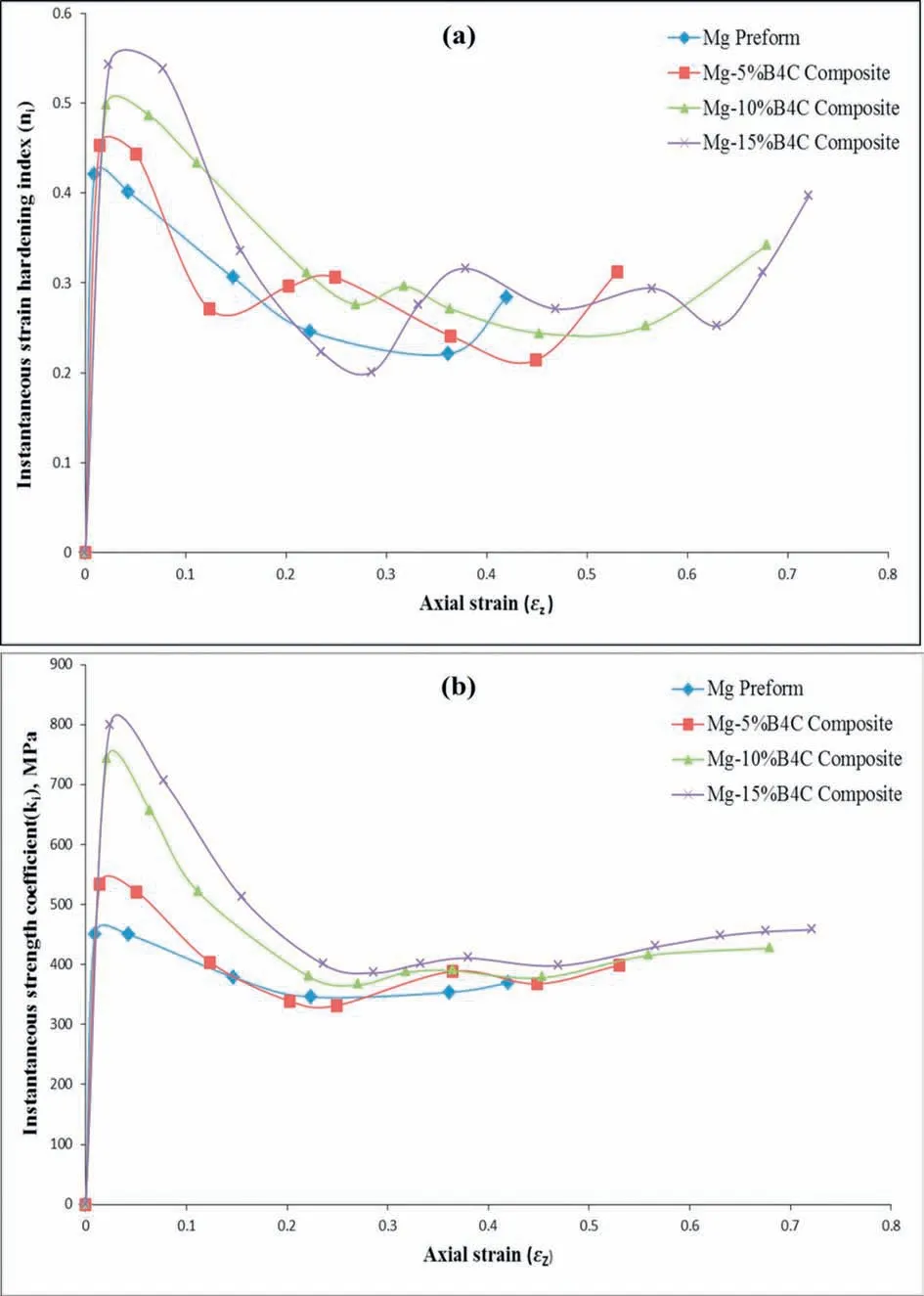
Fig.14.(a) Consequences of the instantaneous exponent of work hardening depending on axial true strain for the Mg-B4C composite with the difference in B4C content (0, 5, 10 & 15%) (b) Consequences of the instantaneous coefficient of strength depending on axial true strain for the Mg-B4C composite with the difference in B4C content (0, 5, 10 & 15%).

4.8.Consequences of the instantaneous coefficient of strength (ki) depending on axial true strain (εz)

The consequences of ki(instantaneous coefficient of strength) depending on axial true strain for the Mg-B4C composite with the difference in B4C content(0,5,10&15%)are given in Fig.14b.The curvature in Fig.14b consists of three levels as like the consequences of ni(Fig.14a).These curves outcomes are in better concurrence with the findings in [40].Fig.14b established that, the major change in the highest kivalue of Mg specimen and Mg-B4C composite.The highest value of instantaneous coefficient of strength for the Mg-B4C composites and comparison with previous reports are shown in Table 9.It is well observed that the ki(instantaneous coefficient of strength) character was affected by boron carbide.This is confirmed by the values presented in Table 9.These curves outcomes are in better concurrence with the findings in [26,39].

4.9.Consequences of an exponent of work hardening (n)depending on wt.% of B4C

The consequences of n (exponent of work hardening) depending on dissimilar wt.% of B4C (0%, 5%, 10% and 15%)of Mg-B4C composite are given in Fig.15a.It revealed that 15% of B4C content composite possesses supreme n value.In the beginning, the n value is lower in zero wt.% of B4C subsequently enhanced gradually and reached the greatest point at 15wt.% of B4C.The exponent of work hardening value depending on their B4C content for the Mg-B4C composite and comparison with previous reports are shown in Table 10.It signifies the work hardening index (n) value for dissimilar B4C content composites.Mg-B4C composite at 15% B4C content reached the maximum value (0.375) than all otherB4C content.Table 10 data signifies that growing of B4C content in the tested composites enhances the n value.It is well noticed that extent of the pore decreases while increasing the B4C wt.%.Composites with lesser pore size have supreme n value [18].The result has good agreement with[26,30,35].

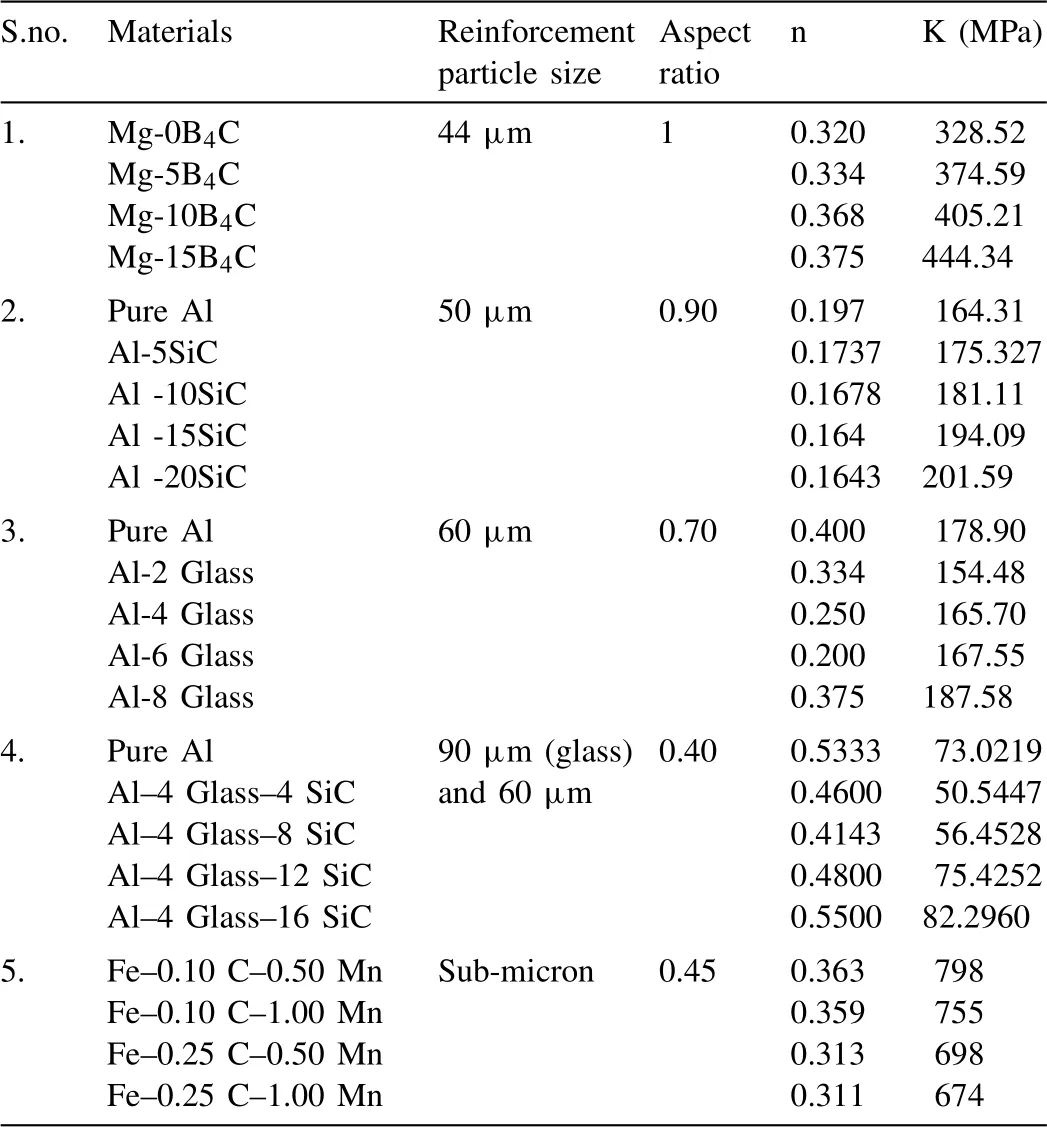
Table 10Coefficient of strength and exponent of work hardening values depending on their B4C content for the Mg-B4C composite and comparison with previous reports [26,30,35].

4.10.Consequences of the coefficient of strength (k)depending on wt.% of B4C

The consequences of k (coefficient of strength) depending on dissimilar wt.% of B4C (0%, 5%, 10% and 15%) of Mg-B4C composite are given in Fig.15b.It has been revealed that the Mg-B4C composites reached the maximum value at 15% B4C for different B4C content viz.0%, 5%, 10% and 15%.As in Fig.15a, the curve displays a growing tendency from zero B4C wt.% to 15 B4C wt.%.Greater k value was attained for high B4C wt.% (15%) composite compared with the other specimen.The 15 B4C wt.% composite shows a greater k value due to its greater relative density and fewer pores.The coefficient of strength value depending on their B4C content for the Mg-B4C composite and comparison with previous reports are shown in Table 10.It signifies the coefficient of strength (k) value for dissimilar B4C content composites.The k value was higher for 15 B4C wt.% composites like the axial true stress.The result has good agreement with[26,30,35].

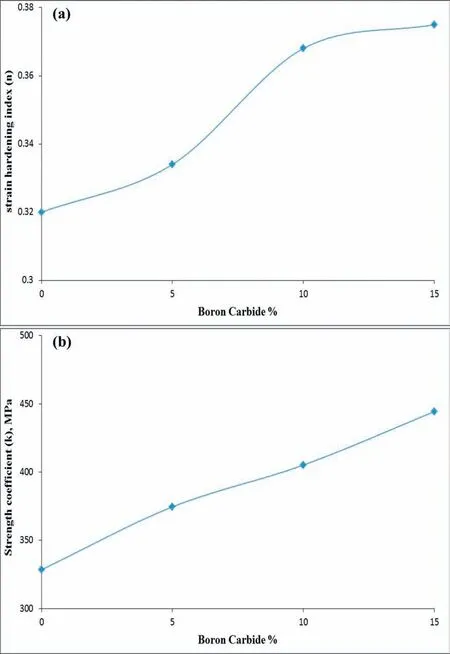
Fig.15.(a) Consequences of the exponent of work hardening depending on the dissimilar percentage of B4C content for the Mg-B4C composite (b)Consequences of the coefficient of strength on the dissimilar percentage of B4C for the Mg-B4C composite.

5.Conclusions

In the present exploration, Mg and Mg-B4C composites are manufactured by using P/M techniques with different B4C content, the characterization was executed with SEM, XRD,and EDS analysis.Formability and work hardening performance of Mg-(5–15%)B4C composites are conducted by cold deformation test and compare this outcome with Mg specimen.Based on the conducted experiments, the discovered conclusions are specified below:

•The EDS and XRD results revealed that, presence of Mg and B4C elements in the Mg-B4C composite seen with different peaks.The existence and distribution of Mg, B,and C particles are confirmed through the elemental map analysis.

•Workability study reveals that the stress index formability factor (βσ) of Mg-15%B4C composite are increased more than the Mg specimen and Mg-(5–10%) composites because of the closure pores in the composites reduce the space by the increasing of B4C content,greater axial strain,and relative density.

•The greatest stress proportion parameters (σθ/σeff&σm/σeff), stress exponent formability parameter (βσ) and relative density obtained for Mg-15%B4C composite.Because the extent of the pore decreases while increasing the B4C wt.%.

•The values of kiand niare enhanced quickly which is maximum in minimum axial true strain thereafter reduced till the closing of pore occurred.Lastly,both values slightly enhanced before the primary crack.It is disclosed that the kiand nivalues are higher for Mg-15%B4C composite and lower for Mg specimen.

•The consequences of k and n depending on dissimilar B4C wt.% displays that the k and n value was higher for 15 B4C wt.% composites.Hence, it is decided that the Mg-15%B4C composite displayed greater workability and work hardening behaviors.