基于KNN和雷达辐射源脉间参数的舰船目标个体识别方法
顾 鹏, 王碧垚, 黄黔川, 李 伟, 张明阳
(电子信息控制重点实验室, 四川 成都 610036)
0 引 言
电子情报侦察作为现代体系作战的重要环节,通过截获并处理雷达辐射源的信号,以查明敌方辐射源的技术特性、地理位置、用途、能力、威胁程度、薄弱环节等信息。然而随着雷达技术的发展,雷达信号的调制方式越来越复杂,特别是相控阵雷达越来越普遍,雷达信号呈现参数多变化快、工作带宽多样化以及特征日益隐蔽的特点,而且不同雷达参数经常出现“混叠”现象使得识别的难度大大增加,因此如何正确识别敌方雷达目标是电子情报侦察的关键技术之一。
雷达目标识别一直是研究的热点领域,但现有资料对基于雷达辐射源脉间参数进行舰船目标个体识别的研究较少。文献[1]介绍了雷达辐射源识别技术发展历程和现状;文献[2]讲述了辐射源个体识别(Specific Emitter Identification,SEI)发展现状,通过使用SEI技术能够利用雷达自身的无意调制信息进行个体识别,但要获取雷达信号脉内信息;文献[3]将时域脉冲波形作为训练样本,使用深度学习方法进行雷达辐射源型号识别,但未能识别到目标个体;文献[4]利用辐射源脉间参数通过特征参数匹配法进行雷达信号识别,要人工预设辐射源脉间参数特征权重及阈值,而且未能识别到目标个体;文献[5]利用航迹关联理论和辐射源配备关系能够进行辐射源平台识别。综上所述,目前雷达目标的识别主要依据雷达信号脉内或脉间特征提取。脉内信息含有丰富的雷达“指纹”特征,但由于网络带宽限制,大多时候脉内中频数据无法进行实时传输处理,只能用于事后分析,并且由于设备存储容量限制无法进行全时段数据采集,脉间参数特征通常只能识别到雷达型号,因此利用雷达辐射源脉间参数并结合其他维度信息进行目标个体识别的研究变得十分必要。本文依据雷达辐射源脉间参数和目标历史航迹数据进行目标个体识别,舰船目标个体识别的难点在于海上同型多目标编队场景,由于雷达相同并且位置接近导致无法进行有效区分,鉴于此本文提出一种基于KNN和雷达辐射源脉间参数的舰船目标个体识别方法,一是能够满足实时处理时效性,二是能够提升同型多目标识别正确率。
1 KNN原理
K最邻近(K-Nearest Neighbor,KNN)算法是距离度量学习方法中的一种,其在对样本进行分类时,是根据查询样本最近的K个近邻的标签来将其分类。KNN最邻近分类算法的实现原理:为了判断未知样本的类别,以所有已知类别的样本作为参照,计算未知样本与所有已知样本的距离,从中选取与未知样本距离最近的K个已知样本,根据少数服从多数的投票法则,将未知样本与K个最邻近样本中所属类别占比较多的归为一类。在scikit-learn中,KNN算法的K是通过 n_neighbors参数来调节的,默认值是5。
如图1所示,若K=3,由于红色三角形所占比例为2/3,绿色圆将被判定为属于红色三角形那个类;若K=5,由于蓝色四方形比例为3/5,因此绿色圆将被判定为属于蓝色四方形类[6]。
图1 KNN原理图
2 基于辐射源脉间参数的目标个体识别
由于KNN最邻近分类算法在分类决策时只依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别,而不是靠判别类域的方法来确定所属类别,因此,对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合[7-9]。海上目标编队跟踪存在多条航迹反复错误交叉的问题,当辐射源目标参数可区分时,能够通过辐射源脉间参数进行关联判决,但当辐射源参数接近或重叠时,仅依据辐射源脉间参数已经无法区分。因此,本文提出一种基于KNN和雷达辐射源脉间参数的舰船目标个体识别方法,能够依据辐射源脉间参数和目标历史航迹对同型多目标进行有效识别,流程如图2所示。

图2 基于KNN和雷达辐射源脉间参数的舰船目标个体识别流程图
2.1 基于脉间参数的雷达辐射源识别
辐射源脉间参数通常由多个参数组成,例如载频、重频、脉宽、天线扫描方式等,用于描述雷达辐射源不同维度的特征。每个参数用特定的类型和参数值来进行表征。不同的脉间参数对应不同的雷达工作模式,一般雷达不同则工作模式也不同,因此,可以利用辐射源脉间参数特征进行雷达辐射源识别。常用的基于脉间参数的雷法辐射源识别方法有两种:1)传统的雷达信号参数模板匹配法,通过设置不同特征参数关联识别门限和权重,将待识别雷达信号与识别库信号数据依次比较并计算识别置信度,选择置信度最高的作为结果输出;2)基于机器学习和深度学习的自动目标特征提取分类方法,如卷积神经网络(Convolutional Neural Network,CNN)等,通过对辐射源历史样本数据进行训练,学习生成网络模型,再将待识别数据输入模型进行分类与预测。本文主要讨论目标个体识别即辐射源搭载平台的识别,平台识别过程中直接利用辐射源型号识别的结果,在此对辐射源型号识别的过程不做赘述。
2.2 基于时间-质心分布的近邻分类改进算法
基于KNN和雷达辐射源脉间参数的舰船目标个体识别方法结合雷达辐射源脉间参数和目标历史航迹数据进行目标个体识别,前置条件是当前的舰船目标个体已识别出,并且辐射源与舰船平台的搭载关系已知。该方法通过设置时间和距离范围来确定K,从而限定当前可能识别的目标范围,范围内每个目标根据历史航迹计算质心并记录最新时间,当有未知辐射源信号到达时,则与范围内雷达目标进行参数关联,关联成功则进一步计算与质心距离来判断目标所属类别,否则认为不是范围内的目标。
在传统的KNN中,若K值过大,非相似数据被包含较多,造成噪声增加而导致分类正确率降低;若K值过小,得到的近邻数过少,会降低分类精度,同时也会放大噪声数据的干扰。因此,本文提出了基于时间-质心分布的近邻分类改进算法,引入了时间-质心的概念。实现方法为:用待分类样本与K个近邻样本质心的距离来代替待分类样本与训练样本之间的距离。

(1)
(2)
F(x)=θ0·x0+θ1·x1+…+θn·xn=θ·X
(3)
式中:θ为质心影响因子向量,由x各阶权重系数构成;X为自变量向量,由x各阶指数构成。
式(3)表示质心与坐标函数方程,影响因子为时间、定位误差等,通过对近邻点进行综合加权,保证时间近、定位误差小的点权值高。
式(1)和(2)表示一定时间和距离范围内,m个近邻样本航迹的质心。通过计算待分类样本与质心的距离确定所属类别,如果待分类样本距离近邻样本的质心越近,则待分类样本与近邻样本越“相似”,预测越准确。
本文选欧氏距离作为距离度量。以计算二维空间中的A(x1,y1)、B(x2,y2)两点之间的距离为例,欧氏距离d为
(4)
实现步骤:
1)通过设置时间和距离范围确定K;
2)确定K个样本所在类别分别为{ω1,ω2,…,ωn};

4)计算待分类样本x0与各类别样本质心的距离dωi,i=1,2,…,n;
5)计算最短距离dωi所对应的类别,即为待分类样本所属类别。
该方法实质是通过计算K个近邻样本质心,放大了不同类样本间的距离,提升了分类正确率。相对于传统KNN算法主要有两个优点:1)当样本不平衡时通过对K近邻点进行加权,保证在进行目标航迹识别时距离近、时间近、定位误差小的点权值高,并通过设置阈值消除噪声干扰;2)通过时间、距离确定K,不需要计算待分类样本与所有样本的距离,只计算与质心的距离,保证正确率的同时降低了运算量。
3 仿真实验与结果分析
场景设置:由于中低轨卫星在一次侦察任务中对海上目标侦察持续时间比较短,考虑舰船目标慢速移动特性及时空约束强的特点,一次侦察任务中目标之间的编队阵型变化不大。所以一个海上目标编队可以看做是在侦察时间内相对位置不变朝着某一固定方向作匀速直线运动。现假设有一个海上目标编队,编队中三艘军舰D1、D2和D3两两相距d,其中D1和D2同时搭载A雷达,D3搭载B雷达,A和B雷达辐射源参数见表1。编队以20节(1节=1.852 km/h)航速朝某一固定方向匀速航行,相对位置保持不变,侦察卫星对目标进行连续跟踪监视。
场景分析:现假定D1、D2和D3航迹均已起始,信号参数已识别,当有未知辐射源信号到达时,先依次与D1、D2和D3三个目标进行参数关联,若关联度小于阈值则认为是不同雷达,否则认为是同型雷达,则利用改进最近邻分类算法计算与质心距离来判决待识别雷达目标所属类别。根据知识库中雷达与平台的搭载关系,若与A雷达参数关联成功则认为该信号属于D1、D2目标,通过计算与D1、D2质心距离判断目标所属类别;若与B雷达参数关联成功,则认为该信号属于D3目标;若与雷达A、B均未关联成功,则认为是新雷达信号。后两种情况依靠参数就能区分目标个体,相对简单,因此本文重点对第一种同型多目标情况进行仿真分析。

表1 雷达辐射源参数
场景仿真:假设卫星一次侦察任务持续10 min,每10 s侦收一个目标信号,共计60次。卫星平均定位精度圆概率误差(Circular Error Probable,CEP)为4 km,当d=3 km时,目标D1和D2真实航迹和观测航迹如图3所示,可以看出目标航迹已经重叠在一起,很难直接区分。

图3 d=3 km时目标D1和D2真实航迹和观测航迹
当d=2 km时,目标D1和D2真实航迹和观测航迹如图4所示,此时大部分航迹已经混叠无法直接进行区分。
假设训练集所占比例为0.75,训练集为45次,测试集为15次,即每次对后15次侦收目标信号进行预测,进行20次蒙特卡罗仿真统计分类正确率,仿真中通过设置时间和距离范围确定K值。
当d=3 km,K=5时,分类正确率如图5所示,其中基于时间-质心分布KNN改进算法和传统KNN算法平均正确率分别为:0.898和0.782。
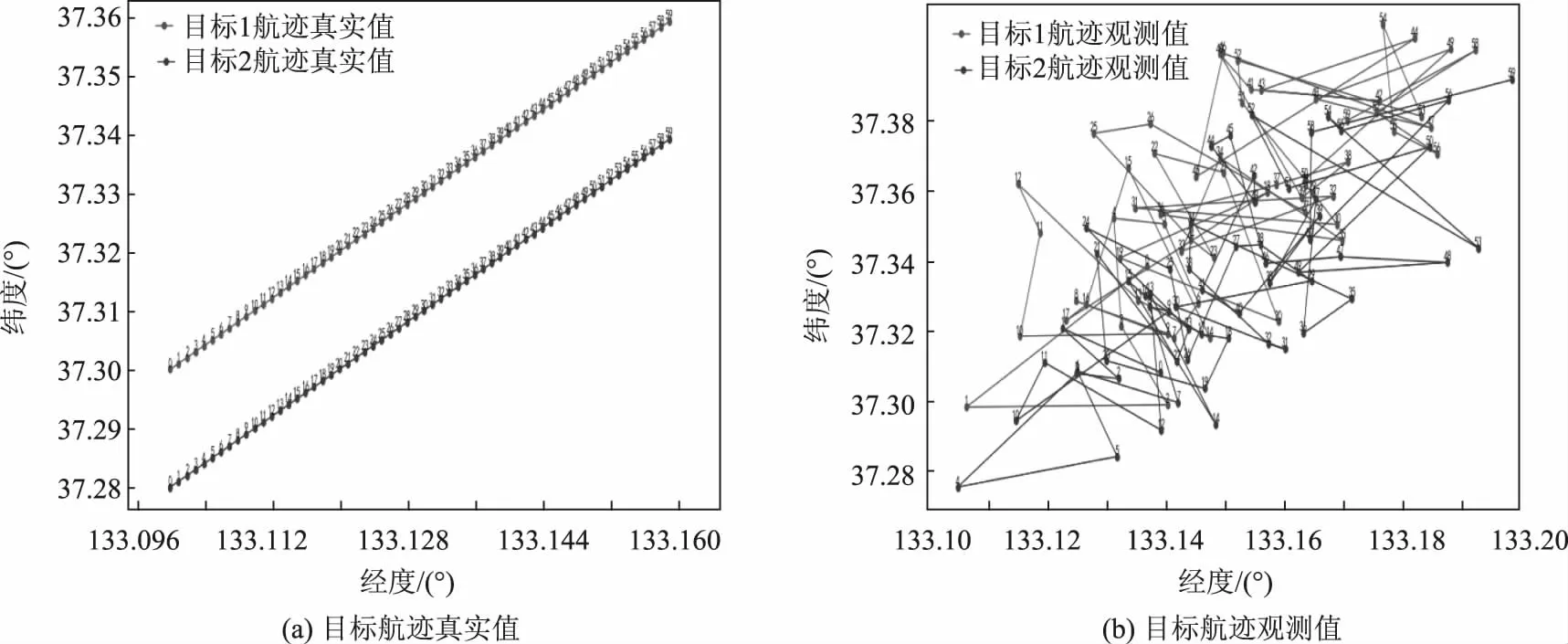
图4 d=2 km时目标D1和D2真实航迹和观测航迹

图5 当d=3 km,K=5时,分类正确率
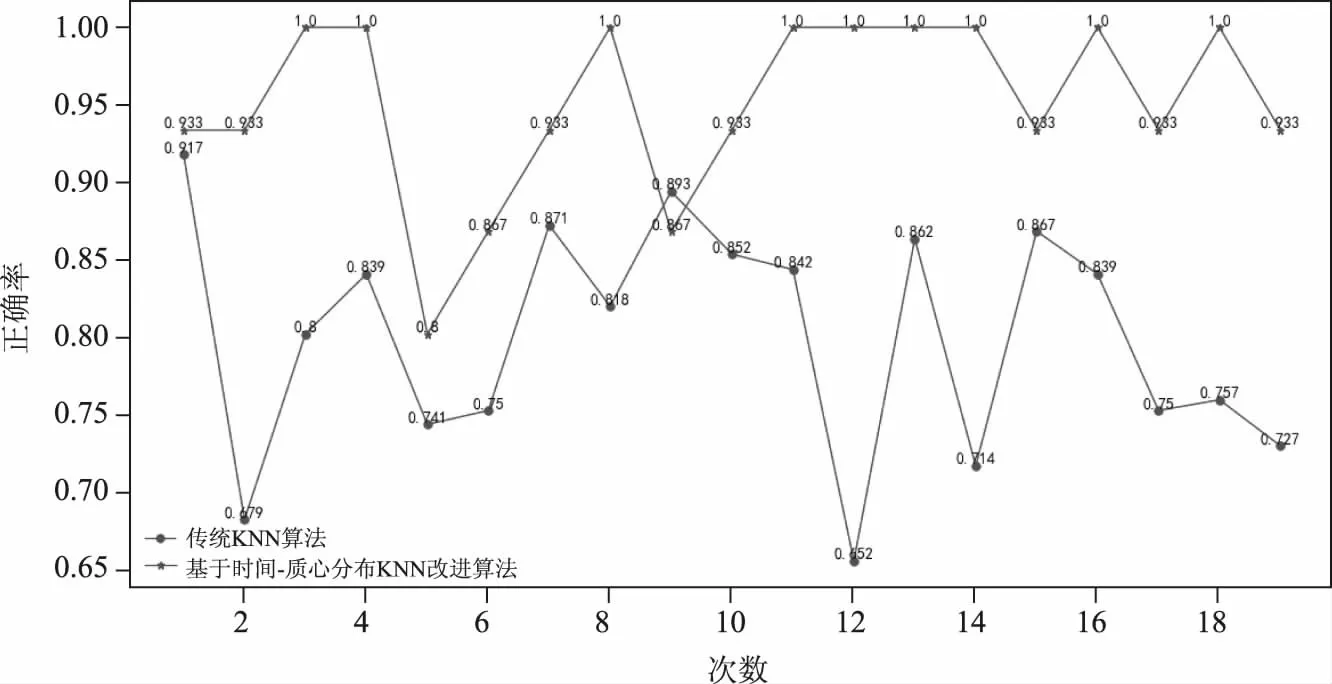
图6 当d=3 km,K=10时,分类正确率
当d=3 km,K=10时,分类正确率如图6所示,其中基于时间-质心分布KNN改进算法和传统KNN算法平均正确率分别为:0.951和0.798。
当d=2 km,K=5时,分类正确率如图7所示,其中基于时间-质心分布KNN改进算法和传统KNN算法平均正确率分别为:0.814和0.691。
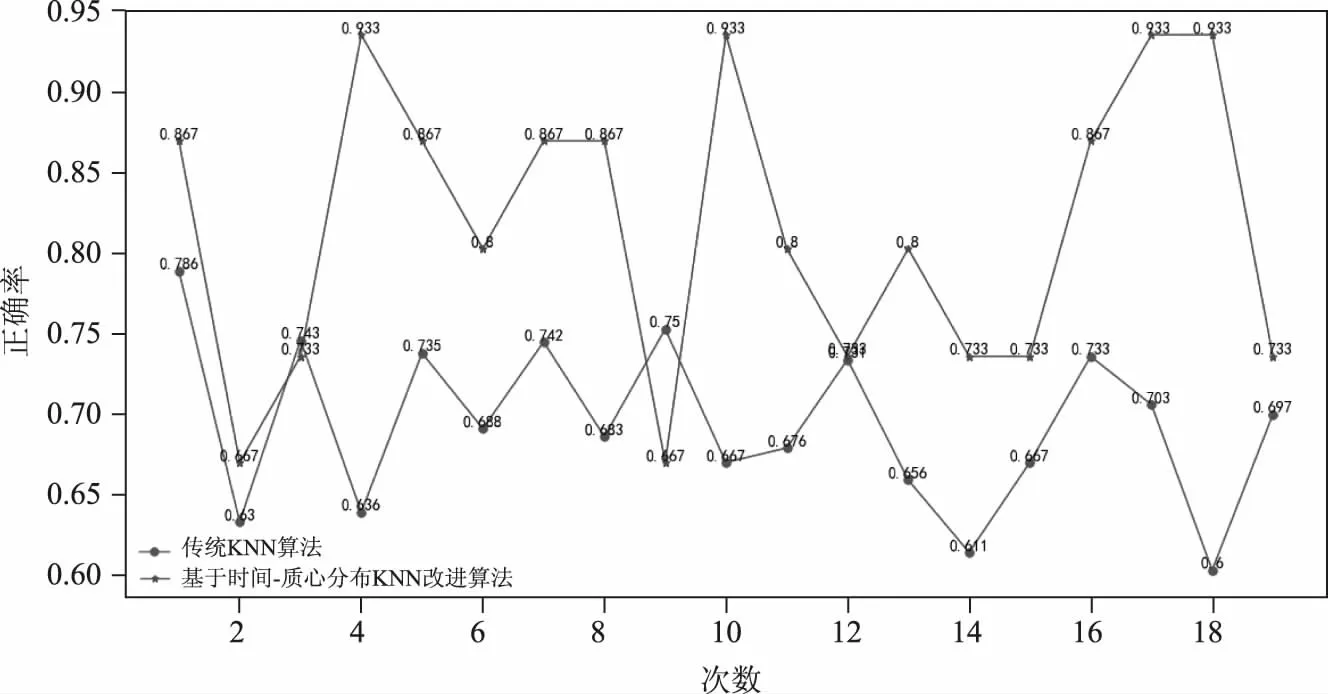
图7 当d=2 km,K=5时,分类正确率
当d=2 km,K=10时,分类正确率如图8所示,其中基于时间-质心分布KNN改进算法和传统KNN算法平均正确率分别为:0.856和0.685。
当d=3 km时,计算K取值对时间-质心分布KNN算法影响,如图9所示。
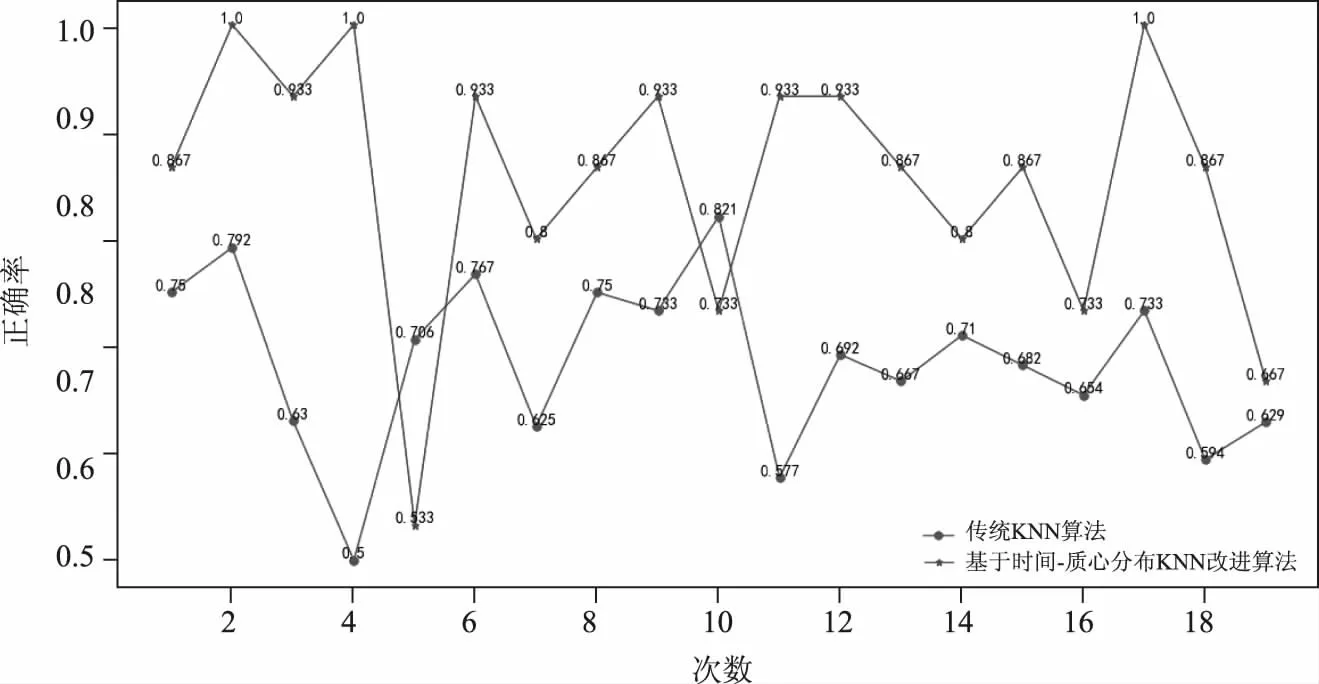
图8 当d=2 km,K=10时,分类正确率
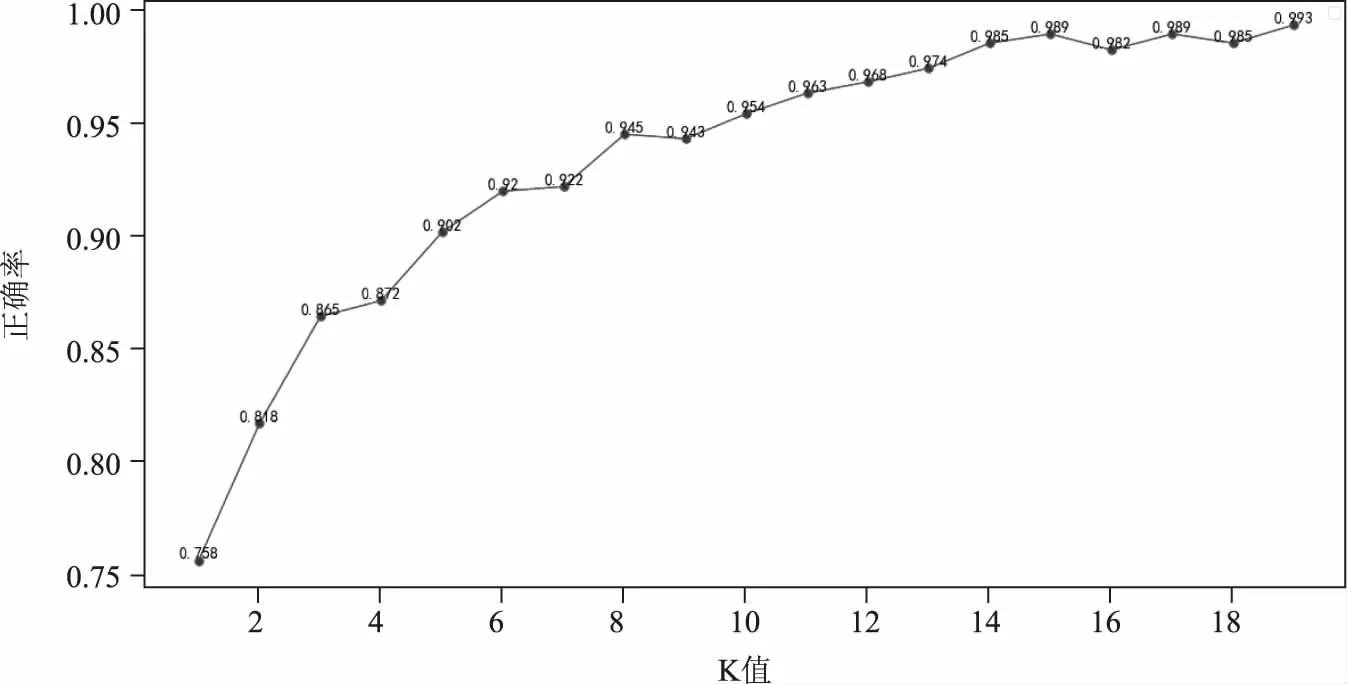
图9 K取值对时间-质心分布KNN算法影响
由前文分析可知,当目标距离小于定位精度时,KNN算法能够利用历史航迹对不同目标进行有效识别,基于时间-质心分布KNN改进算法相比传统KNN算法平均正确率提高至少10%,正确率随着K取值增大而提高,当K=5时,正确率超过0.9,K=10时,正确率超过0.95,但K=10以后提升相对缓慢。
4 结 语
本文研究了一种基于KNN和雷达辐射源脉间参数的舰船目标个体识别方法,能够依据辐射源脉间参数和目标历史航迹对同型多目标进行有效识别,并在传统的KNN算法基础上进行改进有效提升识别正确率,具有识别正确率高,运算量低的优点。下一步将研究对航迹进行跟踪滤波和状态估计,进一步提升识别准确率。

