基于非线性分析的非轴对称磁流体动力学建模

张军

(皖西卫生职业学院，安徽 六安 237005)

0 引言

磁流体在实际应用中又被称为磁液体，属于我国高新研究领域中的代表性产物。此种物质不仅具有常规流动体的特性，也具有固态磁铁的相关性能，主要由直径小于10.0 nm的含磁固态颗粒构成。通常情况下，磁流体在静态环境下无显著的磁吸力，只有在外加磁场或外部环境主动干预的条件下，才会展现出磁力特性。目前，相关磁流体的研究已经覆盖到多个领域，包括地震预测、医院诊疗、声音调试、地质勘查与找矿等。在相关方面的研究中发现，太阳运动与变化的过程受到其本体黑子磁反应的支配，也正因如此，磁流体成为了技术单位工作人员的关注对象。基于理论层面分析，与非轴对称磁流体相关的研究可使用非线性偏微分方程，尽管常规的轴对称也可以用于解释此类问题，但轴对称基于微观层面分析，属于将磁流体的力学参数描述成为了1个平均的模型，经过综合计算与分析后得出的力学参数，也仅是1个环向平均结构，无法对磁场细微变化中环状结构进行深入描述[1]。因此，技术单位在深入此方面研究时，提出用于描述磁流体的非轴对称位形，希望从力学平衡角度对磁流体的物理性能进行细致化阐述。但此种研究结果现如今仍局限在理论研讨层面，相关实践成果较少，无法为后续科研提供有效的数据支撑。因此，本文将基于非线性分析角度，对非轴对称磁流体动力学建模展开研究，以此种方式，为流体动力学研究提供更加可靠的指导。

1 基于非线性分析的非轴对称磁流体动力学建模研究

1.1 非轴对称磁流体动力学特征分析

为了确保构建的非轴对称磁流体动力学模型符合其动力学研究需求，可在开展相关研究前，进行磁流体动力学特征的分析[2]。在对其进行特征分析时，可参照磁流体集成在某种结构中应用的物理方法，构建可用于描述磁流体动力学特征的物理特征结构模型。其结构如图1所示。

图1 描述磁流体动力学特征的物理特征结构模型

从图1中可以看出，将磁流体集成在等离子电弧结构中，流体可以发生磁效应，当对应前端电流可以满足基础需求时，对应结构产生的物理学特性与常规磁场相同。但大部分情况下，电流在结构端的发射量不足，因此，需要采用混合区域发射的电流进行磁场导电供应[3]。综合上述研究，对非轴对称磁流体动力学特征提出假设：磁流体弧柱区域的载流等离子已发生完全电离反应，其中呈现游离状态的等离子大多以带电离子与非带电离子构成，因此在分析磁流体动力学特征时，可直接忽略中性离子对磁场力学的干扰；当等离子参数占据了大部分空间时，可以认为其动力学特征满足le≪d的物理学特性。其中le表示磁流体的平均自由程度，d表示流通空间间距。因此，可以按照流体基本理论进行磁流体动力学参数的描述。考虑到电子的质量小于磁流体中离子的质量，因此在进行磁流体动力学分析时可以忽略由于电子惯性产生的分量。综合上述内容，完成对非轴对称磁流体动力学特征的分析。

1.2 基于非线性分析的建模边界条件设定

在掌握磁流体动力学基本特征的基础上，进行其建模前的边界条件分析。为了确保设定的建模边界条件符合大部分磁流体动力学特性分析需求，此次研究以磁流体集成在电弧结构导电作为参照[4]。综合磁场导电的多种物理学性能与常规磁场条件可知，邻近电弧阴极边界的磁流体电子能量在1.5 eV左右，对应的离子流体的有效能量在0.25～0.40 eV(本次研究取值为0.3 eV)，磁流体中离子运动速度为1.0×104m/s，根据全欧姆定律，进行离子平均电荷参数的设定，即zi=1.85。在此基础上，假设磁流体中离子密度、电子密度的分布均呈现一种均匀状态，此种状态可以表示为

在掌握相关参数后，对磁流体中近阴离子的边界条件进行设定，表达式如下：

(1)

式中：n0表示磁流体中近阴离子的边界条件；γ表示电极边缘发生侵蚀现象的概率，值为115.0 μg/C；mi表示磁流体中单位面积内平均电荷数；uz0表示阴极电极。在完成阴极边界条件的设定后，进行阳极电极边界条件的确定，在此过程中，可假设阳极没有在磁流体中发射带电离子，因此可以将阳极表示为同等电位发射面。但相同的电位在发射过程中存在阳离子层与阴离子层之间的相互干扰作用力，此种作用力会影响到磁流体中电子的传输[5]。因此可将该条件作为阳极边界条件，将此条件融合全欧姆定律，得到边界条件表达式。具体如式(2)所示：

(2)

1.3 基于等离子体密度分布构建多相流方程

在完成对约束条件的分析后，可根据磁流体中等离子体密度的分布进行多相流方程的构建。根据所构建的方程，进行磁流体动力学参数的描述。在此过程中，引进麦克斯韦方程组，对磁流体中等离子体相关参数进行描述，方程组表达式如下：

(3)

式中：E表示磁流体产生电场的强度，单位为V/m；B表示电子能量守恒方程；对应的磁场感应强度计算公式表示为t；J表示磁流体导电后电流密度，单位为A/m2；ρe表示磁流体荷载密度，单位为C/m3；ε表示电解质，通常情况下此数值为常数，单位为F/m。在完成等离子体密度分布的相关参数论述后，建立一个针对磁流体导电的三相函数，其中对应的三相包括电解质、空气、磁流体溶液。在流体界面及其附近的电导率可以使用式(4)进行定义，公式如下：

(4)

式中：ηm表示流体界面及其附近的电导率；ki表示磁流体单相电导系数，单位为S/m；σi为单机体积微分参数。在此基础上，在界面进行磁流体动力学界面跟踪，跟踪的方式是指在界面引入空气，稀释磁流体电解质液体，当前端释放压力后，界面将会产生形变，进行压力梯度的释放。以此种方式，实现对界面等离子特性的跟踪，将跟踪得到的离子数值与麦克斯韦方程组进行对接，得到多个等式，将等式计算结果导入式(4)，即可完成对多相流方程的构建。

1.4 磁流体动力学建模计算参数模拟

在完成建模准备工作后，结合对磁流体力学的非线性分析，进行建模过程中计算参数的模拟[6]。为了确保计算参数的实体化，此次研究以有效电压值为220.0 V的电解槽作为磁流体的载体，参照图1所示的结构，构建一个实体化模型。

在模型中需要将与动力学相关的参数以文件的形式传输到ANSYS Fluent软件当中，方便其实现数值模拟。参数包括：电流流通强度、阳极电流流通时密度、阳极间隙、阴极电流流通时密度、阴极间缝等。为了实现对不同条件下的磁流体结构动力学参数变化态势的分析，需要在参数文件中引入周围空气温度、电解质周围温度、电解质过热度等环境影响参数[7]。同时，在艾迪捷通用热流体软件当中，引入非线性函数，对磁流体结构的动力学变化特征进行预测，将其变化态势的时间步长设置为0.01 s，当各项残差结果均达到预期设置的标准区域范围时，说明非线性函数计算完毕。同时，考虑到各个模拟参数变化特征的稳定性需要，在模拟的过程中忽略温度梯度变化和浓度梯度变化对其造成的影响，并且针对磁流体周围存在电解质的情况，可将电解质当中的气泡影响忽略，从而确保最终模型模拟得出的结果能够符合研究对象实际动力学参数变化。同时，在初始阶段，需要在非线性函数的基础上，将流体初始的流动速度设置为0，将其看作是从静止状态开始。在其动力学参数变化过程中，还应当对三维外磁场数据进行提取并存储[8]。对部分光滑程度较弱的磁流体结构，为了方便模拟，可将其表面空气、槽膛结构等接触面定义为光滑结构面，依此按照上述各个结构的设置实现在ANSYS Fluent软件中对磁流体动力学模拟，得到相应的动力学参数，针对其参数的变化情况对非轴对称磁流体结构的动力学特征进行更加全面的分析。

2 实例应用分析

为进一步验证本文上述设计的动力学建模方法在实际应用中的可行性，以某一非轴对称的磁流体结构作为研究对象，利用本文上述建模思路对该结构进行动力学建模。为了确保实验结果具有可比较性，选择将基于STAR-CCM+的建模方法作为对照组，利用该建模方法对上述结构进行动力学建模，并对两种模型的应用效果进行对比。本文实验当中的非轴对称磁流体结构存在真空电弧，其主要组成包括阴极斑点区、等离子区和阳极鞘层区。在该结构中，当电流未达到足够大时，电极之间的等离子体全部由第一个组成部分提供。同时，在该结构的真空开关中，电子与粒子之间存在极间均满足麦克斯韦分布特点。因此，在实验过程中，为了方便对比，可将真空电弧和等离子体参数设置为定值，将其看作稳态，在特定的开距和电流的情况下，利用两种建模方法实现对其动力学模型的构建。已知非轴对称磁流体结构的电弧电流增加时，其电弧的等离子体和电流的收缩会呈现出不断明显的趋势，而当电极之间的距离增大时，电弧的等离子体和电流的收缩程度同样会呈现出不断明显的趋势。通过对比上述已知变化趋势与最终两种模型得出的数值变化是否一致，可以实现对模型应用效果的分析和验证。因此，在此基础上，完成两种模型的构建后，记录不同电弧电流和电极间距条件下的电弧等离子体和电流的收缩情况。5种实验条件对应参数如表1所列。

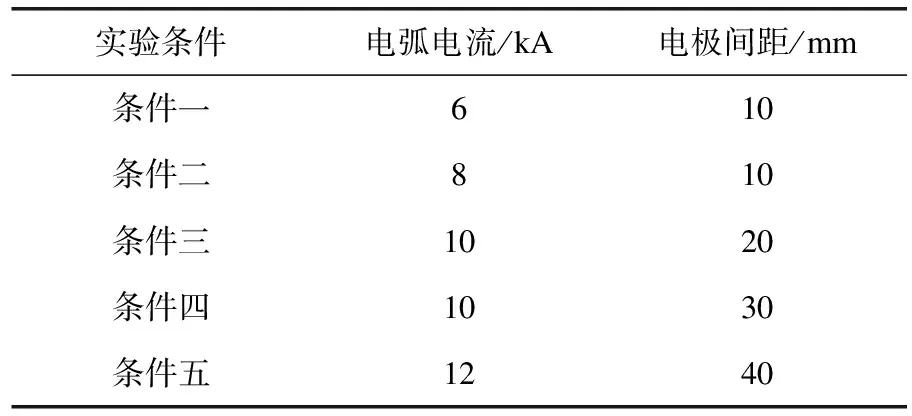
表1 5种实验条件对应参数表

在明确5种不同实验条件后，通过条件一和条件二得出的数据，可以证明在电极间距相同，电弧电流变化时，结构的动力学特征；通过条件三和条件四得出的数据，可以证明在电弧电流相同，电极间距变化时，结构的动力学特征。记录每种条件下对应的2种模型数值模拟结果。为了方便对两种数据变化的比较，将其各自得出的数据结果绘制成表，如表2所列。

表2 两种建模方法下实验对象动力学参数变化

从表2中不同建模方法得到的模拟结果可以看出，本文建模方法下，电弧等离子体和电流均呈现出明显的下降趋势，说明在模拟过程中电弧等离子体和电流均呈现出明显的收缩趋势。在STAR-CCM+建模方法下，电弧等离子体和电流的变化并没有形成规律，收缩态势不明显，无法体现上述已知的该模型在不同实验条件下的变化特征。因此，通过上述实验得出的实验结果可以证明，本文提出的动力学建模方法在应用到实际非轴对称磁流体结构中可以实现对其动力学参数变化的精准模拟，方便对该结构的动力学特征进行更加全面地分析。同时，将本文提出的基于非线性分析的建模方法应用到非轴对称磁流体相似结构的实验中，同样适用，可针对其具备的除电弧等离子体和电流以外的参数进行分析，例如电子温度、轴向电流密度、横向电流密度等，具有更广的适用范围。

3 结语

本文提出基于非线性分析的非轴对称磁流体动力学建模方法，在完成研究后，将基于STAR-CCM+的建模方法作为对照组，实施对比实验，实验结果表明本文提出的动力学建模方法，在应用到实际非轴对称磁流体结构中可以实现对其动力学参数变化的精准模拟，方便对该结构的动力学特征进行更加全面的分析。因此，可尝试将本文设计的方法进行市场推广，为相关科技研究提供更多的技术指导与支撑。