基于TVP-FAVAR模型的中国金融状况指数的构建和预测

2022-07-12 04:57桂文林梁彩丽朱丰毅黄云英

统计与信息论坛 2022年7期

桂文林,梁彩丽,朱丰毅,黄云英

(暨南大学经济学院,广东广州 500632)

一、引言

2008年金融危机前,金融从业者、学术界学者和政策制定者普遍存在一个误解,认为宏观经济稳定自然而然会预示金融稳定,金融稳定是宏观经济稳定显而易见的结果。然而,金融危机于宏观经济大稳定环境下爆发了,甚至直至今日世界上仍有大部分国家的经济增长无法恢复到危机前水平,一些地区的家庭仍存在去杠杆化,即便实施了扩张性货币政策,信贷供给增长也一直缓慢。金融危机对实体经济产生深远的、持续性的影响,反过来,宏观经济的萧条又会引发新的金融危机。金融危机会对实体经济影响之深之广,使得“宏观—金融联系”这一主题获得了政策界和学术界的广泛关注。

值得注意的是,不是所有的危机最终都会演变成系统性金融危机。比如,一个银行部门爆发的金融危机并不一定会蔓延到其他金融部门。但是,像美国次贷危机这种大规模、系统性的金融危机,会传递给全部金融部门,进而影响全部实体经济部门。孟浩等通过TVP-VAR模型研究了各金融市场之间风险传染的网络特征,发现中国的金融市场风险也存在部门间的溢出效应,并且呈现出不稳定性、方向非对称性以及随机性[1]。鉴于不同国家金融市场的规模差异与环境复杂度差异,有必要对不同国家金融市场的关键部门乃至整个金融系统进行监测,以便在可能的危机蔓延到实体经济部门之前及时调整政策或投资方向,朝着金融稳定和宏观经济稳定双赢迈进。因此,建立金融部门与实体经济之间的联系很重要,特别是在金融危机时期。

金融部门与实体经济部门之间的天然联系使得,一旦金融不稳定阻碍了经济增长,实体经济的萧条将进一步加剧金融系统性压力,这样金融和实体经济发展便进入一个恶性循环。因此,监视金融市场、建立金融部门与实体经济之间的联系显得尤为重要,特别是在金融不稳定时期。金融状况指数可以说是金融部门与实体经济之间的一条纽带,透过金融状况指数可以预知未来经济活动的发展趋势。

二、文献综述

金融状况(Financial Conditions)是通过影响经济行为进而影响当前和未来经济状况的金融市场的状态。考虑到金融指标的种类和数量差异,Hatzius等将金融状况指数(Financial Conditions Index,FCI)定义为一个综合指数,用以反映有关经济活动的未来发展状况,供中央银行和市场参与者使用[2]。关于FCI的文献可以追溯到21世纪初。Goodhart和Hofmann在货币状况指数(Monetary Condition Index,MCI)的基础上纳入了股票和房地产价格变量,采用VAR脉冲响应和总需求缩减两种方式,加权平均得到了G7国家的FCI[3],此后便带动了学术界研究FCI的热潮。本文从金融状况指数的变量选择、金融状况指数的构建模型或合成方法以及金融状况指数的应用三个方面进行简要概括。

(一)金融状况指数的变量选择

现有FCI文献主要基于金融与实体经济之间的传递机制来选择用于构建FCI的金融变量。金融变量主要通过对总需求的影响来影响未来通胀。利率、汇率、货币供给与信贷供给作为货币政策工具,通过货币政策渠道调控宏观经济的运行。股价和房价则通过财富效应和资产负债表效应对产出和价格产生影响。因此,构成FCI的指标主要选自上述六个细分金融市场的代表性变量,详见表1。

表1 现有FCI文献中选取的金融市场变量

第一是利率类变量,它是MCI的原始构成变量之一,是一种价格型货币政策工具,是货币政策向实体经济传导的一种标准渠道,利率的调高和调低代表着宏观调控当局的政策立场变化。利率变化通过影响不同种类金融资产的相对价值变化,进而影响投资、消费和总产出。央行将利率下调时对应扩张性货币政策,此时企业融资成本相应减小,投资相应增加,进而总产出增加;利率降低也会使家庭部门减少储蓄,增加对黄金、房地产等保值类产品的投资,同时总消费支出也会有所增加。也就是说,利率对个人和企业的消费行为具有直接或间接影响。

第二是汇率类变量,这也是MCI的原始构成变量之一,汇率的变化反映了本外币交换价格的变化。汇率通过国际贸易、资本跨国流动等渠道影响本国进出口,进而影响总产出和总需求。一国货币当局减少本国货币供给时,本币名义利率上升,持本国货币的资产收益增加,进而吸引国外资本流入本国,本币需求进一步增加,导致本币升值,进而本国产品价格上升,出口减少、进口增加,最终导致本国总产量降低、总产出下降。

第三是资产价格类变量,Hatzius等认为影响企业和个人财富的股价和房价是FCI的自然组成部分[2]。Wacker等在关于FCI研究中考虑了财富效应对产出和消费的影响[4]。由于房产在私人部门财富中的比例高于股权,且房价的波动又比股价的波动低得多,因此房价对财富的影响比股价更重要,房价对私人部门的消费产生更大的影响。

房价和股价也可能通过家庭和公司的资产负债表来影响经济,这就是资产负债表效应。李程等研究发现房地产价格的上涨会推高企业杠杆率和居民杠杆率,形成“房地产价格—杠杆率—金融压力”依次传递的联动机制[5]。资产负债表渠道源自信贷市场的信息不对称问题,进一步导致不利的选择和道德风险。家庭和公司的净资产越低,可用于担保贷款的抵押品越少,逆向选择和道德风险就越严重。资产价格的上涨通过增加抵押品的价值来提高企业和家庭的借贷能力,额外的可用借贷可用于购买商品和服务,从而刺激经济活动。该过程是可以自我强化的,因为额外的可用信贷也可用于购买资产,进一步推高资产价格,而这又会增加借款人的信贷价值,因此Brave等在构建FCI用于描述金融市场状况时都考虑了股价和房价[6-7]。

第四是利差类变量,收益率利差是一种风险度量指标,可能为金融价格影响实体经济的渠道提供信息。透过利差数据,可以将金融事件和商业周期关联起来。固定收益率利差往往在经济衰退之前扩张,又在经济复苏之前收缩。Hatzius等研究认为,FCI应该适当地反映金融部门的风险[2,4]。信贷利差反映了不同市场参与者可接受的资金的相对价格,FCI应反映金融市场的风险度量标准。在金融部门承受压力时,信贷利差可以增加金融压力的可预测性。

第五是货币类和信贷类变量。货币供给是央行通过控制市场上流通的货币数量,直接对中国物价进行调节的一种直接的数量型货币政策工具,也是中国宏观调控的主要手段。信贷供给是央行通过调整商业银行的存款准备金率,进而改变商业银行的放贷标准,间接对中国宏观经济进行调控。货币供给和信贷供给都可以影响企业融资成本和家庭投资与储蓄,是金融市场通过信贷渠道影响实体经济的表现。

(二)金融状况指数的构建方法

与MCI的构建一样,构建FCI的方法通常分为两大类:加权求和法和主成分或因子分析法。加权求和法就是对选取的金融变量的缺口进行加权平均,即:

(1)

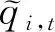
主成分或因子法则是从一组指标中提取主成分或公共因子,以捕获信息集中的最大变化,通过对主成分或公共因子而不是构成变量本身进行加权平均得到FCI。现有文献主要有两种可选的主成分或因子分析方法:第一是标准主成分或因子分析,第二是时变参数因子增广向量自回归(time-varying parameter factor-augmented vector autoregression,TVP-FAVAR)模型或动态因子模型。这两种方法的主要区别在于:标准主成分或因子分析假定每对金融变量之间的关系是恒定的,而TVP-FAVAR或动态因子模型则允许这种关系在每个时间点都发生变化。

1.加权求和法

第一,根据大型宏观经济模型或结构模型估计的系数进行加权平均。Goodhart等证实了基于结构模型得到的权重优于其他方法估计的权重,因为它考虑了经济的结构特征以及所有宏观经济指标的相互作用[3]。王维国等利用中国数据估计了小型宏观经济模型,通过模型系数加权平均测算了中国FCI,并指出FCI的走势与中国金融环境的实际波动有紧密的联系[8]。但是,在一些国家特别是发展经济体中,大型宏观经济变量的可获取性较差,并且数据处理较为复杂,因此学者轻易不使用这种方法。

第二,根据VAR模型的脉冲响应大小进行加权平均。该方法可以在特定时期内根据构成变量对目标宏观经济变量(如产出增长或通货膨胀)的相对影响来加权平均得到FCI。换句话说,在VAR模型中,FCI权重是根据目标宏观经济变量对每个构成变量的累计脉冲响应得出的。Goodhart等基于VAR脉冲响应构建了G7国家、美国的FCI[3]。徐国祥等基于VAR或TVP-VAR模型的脉冲响应函数加权平均得到了中国FCI[9-11]。但是,VAR有一个局限性,那就是每个构成变量的权重通常是固定的。

第三,根据总需求缩减式的系数大小和显著程度进行加权平均。从总需求缩减式推导FCI的一个明显优势是,可以确定每个潜在的货币传导渠道对实体经济的影响。金融市场在转移货币政策对实际经济活动和通货膨胀的影响方面起着相当重要的作用。Goodhart等使用OLS估计了简化形式模型,然后评估了七个发达国家FCI的样本外预测[3]。他们的结果表明,基于简化形式模型的FCI通常比基于VAR模型的性能更好。陆军等也基于总需求缩减式构建了中国FCI[12]。但是,使用简化形式模型估计FCI的权重时,现有文献至少有三个不足:第一,没有考虑FCI的提纯问题;第二,参数估计的准确性堪忧;第三,模型假设过于严格,实际应用中难以做到。

2.主成分或因子法

主成分分析(PCA)是一种统计技术,它试图捕获信息集中最大的变化。在这种技术下,FCI被视为金融系统多个指标的共同变动。Brave等分别采用PCA方法构造了加拿大、美国、挪威和欧元区FCI[6,13]。邓创等通过提取前8个主成分,并以各成分的方差贡献率为权重,测算出中国的FCI,用以衡量中国金融周期的波动状况[14]。

然而,采用标准PCA提取FCI存在明显的不足之处。Wacker等的研究结果表明,标准PCA假定每个金融变量在样本期内具有恒定的载荷,即金融变量之间的相关结构保持不变,这并不符合真实的情况[4]。为避免固定载荷问题,Koop等开创了使用带有随机波动率的TVP-FAVAR模型构建FCI的先河,允许因子载荷和VAR系数动态演变,考虑了FCI与目标经济变量的联动性[7]。TVP-FAVAR模型克服了标准PCA中固定载荷的假设缺陷,并在TVP-VAR中检验FCI对目标经济变量的预测能力,因为一个优良的FCI能够准确地预测目标经济变量。陈磊等也采用TVP-FAVAR模型测算了中国的金融状况指数[15-16]。Zhu等则在TVP-FAVAR模型的框架内基于TVP-R-SV算法用小型金融变量集合测算了英国FCI,并强调单就预测经济发展而言,TVP-FAVAR模型是构建FCI的最佳模型[17]。

动态因子方法是从一系列宏观经济变量中找到公共因子系列,并用公共因子衡量这些变量的共同变动。在动态因子模型中提取重要金融变量的潜在公共信息作为FCI,是满足FCI的构建需求的。因此,除了提取主成分作为FCI外,还可以基于动态因子模型提取公共因子作为FCI。Matheson在因子法的基础上考虑了模型的时变性,采用动态因子模型构建了美国和欧元区的FCI,表明简单的VAR加上估计的FCI对产出缺口、核心通胀和实际短期利率的预测性能比其他一系列模型要好[18]。肖强等使用动态因子模型测度了中国FCI,尚玉皇等则结合高频与低频数据,建立了混频动态因子模型测度中国FCI[19-20]。

(三)金融状况指数的应用

FCI用于研究金融市场与实体经济之间的联系、预测未来经济活动的变化。Hatzius等证明了FCI是经济活动的可靠预测指标[2,7]。余辉等指出FCI与通胀存在因果关系,FCI可以作为通胀的先行指标[21]。徐国祥等通过谱分析发现FCI与中国通胀和经济一致指数具有较强的相关性和领先性,证明FCI是宏观经济的先行指标[9]。邓创等通过脉冲响应研究了FCI波动与宏观经济的动态互动和非对称效应,指出FCI波动领先于中国的经济景气波动,金融状况向好的加速效应比金融状况恶化的负面效应更显著[14]。

FCI可以作为金融市场压力的领先指标和预警信号。一个全面的FCI可以监控和评估整个金融市场的压力水平,可以更好地描绘历史性金融事件,如重大金融危机。苏黎世联邦理工学院从400多个金融变量组成的面板中提取主成分,编制KOF晴雨表以度量瑞士的商业周期。Hakkio等从11个金融指标中提取第一个主成分构建了堪萨斯城联储的FCI[22]。Brave等则使用动态因子模型编制了芝加哥联储的金融状况指数(NFCI)以及剔除宏观经济成分后调整的国家金融状况指数(ANFCI),并指出这两个指标都是金融压力的主要预测指标[6]。此外,FCI可以提高宏观审慎预警信号模型的统计能力和信息内容。

除了为金融市场压力和宏观经济发展提供预警信号外,FCI还可以帮助政策制定者更好地理解不同金融冲击对实体经济的传导路径及其影响,以便从金融稳定局面出发,制定既能保金融稳定又能促经济发展双目标的货币政策。此外,金融稳定机构还可以将FCI用于衡量旨在减轻金融动荡的政策措施的影响。

(四)文献评述

梳理文献后发现,现有的关于FCI的测度研究尚有改进的余地。已有文献在建构FCI时,或者未考虑金融环境和经济结构的变化而采用常系数VAR模型和标准PCA,或者考虑了参数的时变性但未能实证检验变量选择的动态性对FCI精度的影响。实际上,随着经济结构的变化,不同时点影响金融状况的变量可能不同,相应变量获得的权重也会不同。一个典型的例子就是,次贷危机爆发前后房地产市场对金融系统的影响更显著,房地产市场变量应纳入FCI构建当中。此外,一个良好的FCI不仅要考虑结构突变,还要进行“提纯”,这两点在选择构建方法时应重点考虑。

为此,本文明确考虑了经济结构的突变性和FCI的“纯粹性”,采用Koop等提出的一种新的构建FCI的TVP-FAVAR模型,允许不同样本点选择不同的金融变量,并且赋予各自不同的权重来合成中国FCI[7]。确切地说,采用动态模型选择与平均(dynamic model selection and averaging,DMS和DMA)技术,以动态方式实现模型的选择与平均,提高FCI的测度精度。其中,DMS在每个样本点上选取单个最佳的TVP-FAVAR模型来提取FCI,而DMA则平均所有样本点的最佳模型规范,以降低FCI的测度误差。

可见,相比于已有的研究,本文的边际贡献主要有:(1)有别于以往文献考虑单一通货膨胀率,本文在评估FCI的质量时同时考虑了通货膨胀率和宏观经济景气一致指数,全面地覆盖了多种评价指标;(2)在短期利率方面新增了上海银行间7天同业拆借利率,在房地产价格方面新增了住宅物业价格指数,指标的范围广,信息充分;(3)重点增加了三个利差指标,在FCI的构建中考虑了潜在金融市场风险对金融市场整体形势的影响,囊括了更多的金融市场信息;(4)相比以往文献构建中国FCI之后使用简单的一元回归模型预测通胀,而本文不仅在TVP-FAVAR模型中提取FCI,也在TVP-VAR模型中对通胀和宏观经济景气一致指数两个变量进行预测,捕捉了FCI与两个宏观经济变量之间的动态互动关系,同时进行了模型选优。

三、金融状况指数的测度方法

(一)TVP-FAVAR模型介绍

借鉴Koop等构建的TVP-FAVAR模型,本文令xt(t=1,2,…,T)为n×1维金融变量矩阵,yt是s×1维宏观经济变量。在本文的实证研究中yt=[πt,gt]′,其中πt表示通货膨胀率,gt表示宏观经济景气一致指数[7]。滞后P阶的TVP-FAVAR模型如下:

(2)

(3)

TVP-FAVAR模型由两个方程组成,一个方程允许从金融变量xt中提取潜在的公共因子ft(FCI),另一个方程允许对FCI与目标宏观经济变量的动态关系进行建模。第一,与大多数学者提取FCI后在另外回归模型中进行预测不同,使用包含FCI在内的多元系统预测宏观经济变量,能够更好地表征它们的共同变动和相互依赖性。第二,在式(2)右边加入yt这种设定能够从FCI中剔除宏观经济成分的影响,使最终估计的FCI能纯粹地反映金融市场的真实状况。值得注意的是,这种方式只能剔除当前宏观经济状况对FCI的影响,FCI仍能反映对未来宏观经济的预期,FCI的本质功能没有改变。

在式(3)的左边包含yt是为评估FCI提供一个度量。因为一个尽可能准确地预测yt的FCI才是好的FCI。基于FCI对yt的预测来不断更新FCI是本模型的特点。在式(2)中包括yt并不是建立经济结构模型(SVAR或DSGE等),也不具备结构模型的经济含义。因此,结构模型所引起的问题,如结构VAR通常涉及反映假定因果结构的变量排序问题在此无需解决。

λt=λt-1+vt

(4)

βt=βt-1+ηt

(5)

其中,vt～N(0,Wt),ηt～N(0,Rt)。最后,式(2)～(5)中的所有扰动项彼此不相关。

通过对TVP-FAVAR模型施加约束,可转化成其他相似模型。(1)将λt和βt约束为常数(Wt=Rt=0),则退化为FAVAR模型。(2)若提取的因子个数为零(ft=0)时,则退化为TVP-VAR模型。(3)若提取的因子个数为零且λt和βt均为常数,则退化成VAR模型。

(二)单个TVP-FAVAR模型的估计

为了实现在递归预测中提取FCI、减少模型估计负担、简化FCI的估计,本文借鉴Koop等的两步估计法,将方差折现思想与卡尔曼滤波器相结合,以获得状态变量ft的后验分布以及时变参数θt=(λt,βt)的分析结果[23]。但是,鉴于式(2)和(3)中的潜在因子ft和载荷λt均不可观测,传统卡尔曼滤波器递归用于状态空间模型是不可行的。为此,本文采用了Doz等的双重线性卡尔曼滤波算法,同时对不可观测的状态向量ft和时变参数θt=(λt,βt)进行快速估计[24]。

TVP-FAVAR模型中的误差协方差矩阵通常使用多元随机波动率模型来建模,但该方法计算较为繁杂。为了减少计算负担,递归使用方差矩阵折现方法来估计协方差矩阵(Vt,Qt,Wt,Rt)。对于Vt和Qt,采用指数加权移动平均(exponential weighted moving average,EWMA)滤波器来估计,EWMA依赖于延迟因子κ1和κ2。协方差矩阵Wt和Rt则采用Koop等使用的遗忘因子模型来估计,遗忘因子模型依赖于遗忘因子κ3和κ4[23]。延迟因子和遗忘因子的作用相似,延迟(遗忘)因子的取值越小赋予近期观测值的权重越大。特别地,当κ1=κ2=1时协方差Vt和Qt退化为常数;当κ3=κ4=1时,Wt=Rt=0,此时λt和βt是常数。

(三)多个TVP-FAVAR模型的选择与平均

根据每个时点进入TVP-FAVAR模型的金融变量不同,本文共需处理Mj(j=1,2,…,J)个模型。通过对时点t未进入TVP-FAVAR模型的特定金融变量组合的因子载荷限制为零,或者将xt中未进入的各列金融变量取值为零,得到特定的TVP-FAVAR模型。每种金融变量组合而成的模型Mj的形式如下:

(6)

(7)

当涉及多个模型时,贝叶斯模型选择或贝叶斯模型平均就显得特别有效。但是,考虑到本文所构建的FCI的时变性,在DMS中,允许每个时点进入TVP-FAVAR模型用于提取FCI的金融变量集合是动态的;在DMA中,允许使用动态权重来平均各个模型规范以降低风险。

给定一个初始状态π0|0,j,j=1,2,…,J,基于模型遗忘因子的模型预测方程和模型更新方程分别为:

(8)

(9)

其中fj,t|t-1是模型Mj的拟合优度,本文将宏观经济变量的预测可能性pj(yt|t-1)设置为拟合优度。这里的α(0<α≤1)也是一个遗忘因子,与前文的延迟(遗忘)因子(κ1,κ2,κ3,κ4)含义相同。较低的α意味着较快的模型切换速度。特别地,当α=1时,DMS和DMA退化为普通的贝叶斯模型选择/平均(BMS/BMA)。

初始值π0|0,j一经确定后,卡尔曼滤波器就可以估计出时点t应用模型Mj的概率πt|t,j,πt|t,j最大值所对应的单个TVP-FAVAR模型便是用于提取当期FCI的最佳模型,或者根据DMA加权平均后得到更稳定的FCI。

四、金融状况指数的测度研究

(一)具体变量的选择

FCI的主要目标是衡量金融市场的不稳定状态,并将各个重要细分市场的波动状态及互动效应汇总成一个连续的统计量。本文的研究目的是构造一个能反映金融市场不确定性并能更准确地测度宏观经济变量的FCI。促进经济增长和稳定物价是中国宏观调控的两个主要目标,GDP增长率和通货膨胀率作为典型宏观经济变量,应该作为评估FCI测度效果的首选指标。但是,GDP只公布季度数据,因此本文选取了宏观经济景气一致指数代替GDP增长率。通胀率和宏观经济景气一致指数均为原始值减去100。

从已有的FCI文献来看,由于构建FCI的初衷不同、数据有效性不同、模型复杂度与估计难度不同,导致选取哪些金融变量并没有一致的结论。但能确定的是,对金融状况影响较大的典型变量几乎存在于现有FCI文献中。如短期利率、有效汇率、股价指数、房屋价格通过货币政策效应、财富效应和资产负债表效应影响中国经济,是FCI的重要构成变量。货币供应量和信贷供给作为中国数量型货币政策工具,它们的调整直接影响消费和投资,也是中国FCI的重要组成部分。长期以来,收益率曲线、收益率利差一直用作衡量未来经济活动的金融指标,也是FCI的常见组成部分。此外,全球经济一体化和金融自由化为金融风险的跨国传播提供了可能,国际金融市场的风险积累也会蔓延到本国当中,因此衡量国际金融走势或风险的指标在构建FCI时应当予以考虑。

构建FCI的原始指标信息详见表2,该表报告了每个指标的名称、标识、样本开始年月、选取依据。与陈磊、罗煜等做法不同:第一,本文在评估FCI的质量时同时考虑了通货膨胀率和宏观经济景气一致指数两个宏观经济变量,并非单一的通货膨胀率,从多个角度去评估本文构建FCI所采用方法的优越性;第二,本文在短期利率方面新增了上海银行间7天同业拆借利率,在房地产价格方面新增了住宅物业价格指数,指标的涵盖范围不同,提供的有用信息也会不同;第三,本文重点增加了三个利差指标(泰德利差、1年与3年国债利差、3年与3个月国债利差),在FCI的构建中考虑了潜在金融市场风险对金融市场整体形势的影响[15-16]。

表2 构建FCI的原始指标信息

(二)变量预处理

在构建FCI之前,有必要对各变量进行预处理。第一,使用X-12方法对各原始指标进行季节调整,剔除各原始变量的季节成分,得到序列的趋势循环成分。第二,剔除通货膨胀因素影响得到实际值,其中利率和收益率变量,用名义值减去同期的通货膨胀率得到实际值,其他以人民币标价的变量则用名义值除以1999年为基期的中国定基CPI得到实际值。由于布伦特原油价格和伦敦黄金价格是用美元标价,因此这两个变量的实际值是用BIS公布的以2010年为基年的美国定基CPI计算得到的。第三,对样本期内取正值的变量进行对数化处理以减小异方差性。第四,通过HP滤波分离出序列的趋势成分和循环成分,得到缺口序列,利率、收益率及利差变量则保持水平值。

为了保证各序列的平稳性,避免“伪回归”问题,还需要对各缺口序列进行单位根检验。值得注意的是,预处理过程并不对缺口序列进行标准化处理,所有标准化操作在建模过程中完成,在构建FCI前消除各序列的量纲影响,让所构建的FCI在均值处上下波动,便于分析不同时期中国金融市场运行状况。所有数据预处理环节均由EVIEWS 9.0完成,预处理后各指标的描述性统计详见表3。

表3 变量描述性统计与单位根检验结果

单位根检验采用常用的ADF检验。检验结果显示,除M1缺口的显著性水平为7%,通货膨胀率的显著性水平为4%外,其他缺口序列的显著性水平均低于1%。因此,通货膨胀率、宏观经济景气一致指数和各金融变量(缺口)均满足主成分(因子)分析及TVP-FAVAR模型的建模需求,可以直接进入模型。

(三)金融状况指数的测度

本文的样本区间为2000M01—2020M11(即2000年1月至11月,下同),但在上文的变量选择中,某些金融变量在初期存在缺失值(如shibor是从2006M10开始)。所有18个金融变量(缺口)中,住宅物业价格指数的缺失比例为53%,上海银行间7天同业拆借利率的缺失比例为32%,伦敦黄金价格的缺失比例为14%,社会融资规模、国债收益率或利差的缺失比例为10%,其他变量在每个样本点都有观测值。虽然每个指标的观测起点不一致,但本文在TVP-FAVAR模型中所采取的卡尔曼滤波可以将某些不存在观测值的指标当作信息缺失,在某个样本点进行卡尔曼估计更新时暂时不提供有效信息,但这并不影响最终的优化结果。因此,在单个TVP-FAVAR模型中,在卡尔曼滤波估计更新中,少量缺失值并不影响最终估计的FCI的质量。

但是,在DMS和DMA中,候选变量在样本初期没有观测值是不允许的,因为某个时点(如2006M10)的FCI值是在至少观测到一个金融变量后才开始估算的,而DMS有可能仅选择该期间都缺失的金融变量(如shibor和property)来提取FCI。在这种情况下,在指定时间段内提取到的FCI值为零,是无效的。为了避免这种意外发生,本文借鉴Koop等的做法,选取一个或几个金融变量始终包含在模型中,这些被固定的金融变量的观测区间为2000M01—2020M11,横跨了整个样本区间[7]。本文将national、REER_gap、shangzheng_gap、house_gap以及M2_gap共5个金融变量(缺口)始终包含在模型中,这是邓创等用于构建FCI的5项指标[10,11,19,26]。也就是说,每个样本点的FCI值至少是基于这5个变量(缺口)提取的,仅对剩余的13个金融变量执行DMS和DMA。因此,本文的模型空间为J=213=8 192,也就是8 192个TVP-FAVARs模型。

接下来便是设置模型的超参数与初始条件。首先设置因子ft(FCI),时变参数λt、βt和时变协方差Vt、Qt的初始值,要进行DMS和DMA还要设定π0|0,j(j=1,2,…,J)。这些超参数的初始值为f0～N(0,4)、λ0～N(0,4×In(s+1))、β0～N(0,VMIN)、V0=1×In、Q0=1×Is+1、π0|0,j=1/J。其中VMIN是对角协方差矩阵,服从Minnesota先验分布,远期观测值的权重较小。此外,Wt和Rt无需初始化,因为它们的估计值与从卡尔曼滤波中估计得到的协方差矩阵成比例。对于延迟因子与遗忘因子,,本文借鉴Koop等的做法,选择κ1=κ2=0.96,κ3=κ4=0.99,模型转换的遗忘因子α=0.99,这意味着使用相对缓慢变化的模型概率来实现DMS和DMA[7]。

1.单个模型测度的金融状况指数

图1报告了使用所有18个金融变量以TVP-FAVAR模型、FAVAR模型和标准主成分分析三种方式测算的金融状况指数。实线是基于TVP-FAVAR模型提取的FCI,短划线是采用FAVAR模型提取的FCI,这两个模型均采用两步估计法进行快速估计,唯一的区别在于TVP-FAVAR模型的参数具有时变性,而FAVAR模型的参数在样本期内是恒定的。圆点线是基于标准主成分分析,从所有18个变量(缺口)中提取第一主成分得到的FCI。可以看出,TVP-FAVAR模型、FAVAR模型与主成分分析估计得到的FCI是极为相似的,TVP-FAVAR模型估计得到的FCI仅在少数样本点处与其他两个FCI不同。这进一步支持了以主成分估计值作为因子Ft的初始估计值是可行的,得到的估计值也是一致的、稳定的。

图1 所有18个变量测度的FCI

图2报告了通货膨胀率与基于单个TVP-FAVAR模型估计得到的FCI的对比走势图。由于FCI是从所有18个标准化的实际金融变量(缺口)中提取的,因而得到的FCI也是标准化的,为了更直观地对比,用于比较的通货膨胀率是经过标准化处理的。可以发现,TVP-FAVAR模型估计的FCI与中国通货膨胀率走势基本一致,特别是在2000—2013年间,均具有明显的相似的周期波动特征。还可以发现,两步法估计的TVP-FAVAR模型提取的FCI领先于通货膨胀率大约1年,也就是说本文所构建的FCI包含了未来通货膨胀的有用信息,可以作为通货膨胀率的有用预测因子。

图2 标准通胀与单个TVP-FAVAR模型估计的FCI

图3报告了宏观经济景气一致指数与基于单个TVP-FAVAR模型估计的FCI的对比走势图。与通货膨胀率一样,此处的boom也是经过标准化处理的,其取值小于零代表宏观经济不景气,反之亦然。可以发现,单个TVP-FAVAR模型提取的FCI与boom的走势更吻合,并且领先于boom 3～6个月。还可以发现,严重紧缩的FCI可以预示未来短期内宏观经济的不景气,但二者的萧条程度并不成正比。对于FCI来说,其在2008年金融危机期间的紧缩程度要大于2020年初“新冠肺炎疫情”期间的紧缩程度;而对于boom来说,其在“新冠肺炎疫情”期间的不景气程度远大于国际金融危机时期。这说明“被迫”停工停产对中国经济发展的影响是前所未有的。FCI确实包含了未来宏观经济状况的信息,可以用来预测宏观经济状况,进而指示未来的经济活动。

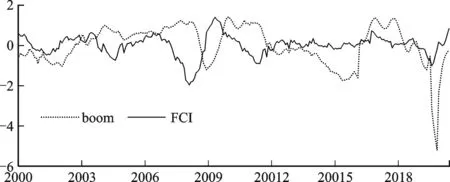
图3 一致指数与单个TVP-FAVAR模型估计的FCI

2.动态模型选择与平均测度的金融状况指数

图4报告了DMS中每个变量(缺口)进入TVP-FAVAR模型的动态概率。若变量在样本初期存在缺失值,则其概率为零。TED和M1_gap在2012年之前并没有进入模型,2012年之后的概率也很小。这并不是因为它们对金融市场压力没有贡献,而是因为它们不能提供与固定在模型中的同类变量(缺口)互补的信息。两个利差风险变量3y/3m spread和10/3y spread的概率在整个样本期间保持在0.5左右,说明这两个变量稳定地为金融状况提供了有用的信息。有趣的是,shibor在2006—2012年间以极高的概率始终保持在模型中,其后概率虽然有所降低,但整个样本期内的概率保持在0.6以上,这说明national并不能代替shibor,即使它们有相似的走势(见上文的金融变量选取)。

图4 金融变量(缺口)进入模型的动态概率

比较明显的还有USER_gap,其概率走势呈现抛物状,从样本早期的零概率逐渐上升到金融危机期间的最高点,而后逐渐下降并于样本后期保持在0.5左右。这也说明USER_gap包含了REER_gap中没有的信息,它对金融状况的贡献是不可代替的。AFRE_gap和loan_gap是两个相似的信贷变量,AFRE_gap的概率始终在0.5处波动,而loan_gap前期概率趋近于1后逐渐下降,在2008年前后隆至最低点又缓慢提高,随后在0.4趋于稳定。最后是两个国际金融市场变量,可以发现brent_gap进入模型的概率较小,而gold_gap的概率保持在0.5左右,变动不大。

综合来看,大部分变量的概率是动态性的,有的变量在某个时期进入模型,又在某个时期离开了模型,反映了同一个子金融市场在不同时期对整体金融市场的不同影响。这进一步突出了DMS和DMA技术在TVP-FAVAR模型中的优势。

图5报告了每个样本点对应的模型大小,除了始终包含在模型中的五个典型变量之外,每个样本点还有4～6个变量进入模型,换句话说,整个样本期内用于提取FCI的金融变量缺口大约为9～11个。图5还显示出,样本点越靠后,TVP-FAVAR模型动态选择进入的金融变量数量呈现递增的趋势,这说明随着中国金融市场的发展,金融市场各部门对中国金融状况的影响不是一成不变的,而是动态变动的。还可以看出,金融危机前每点TVP-FAVAR模型的大小保持在9左右上下波动,达到局部稳定的状态。

图5 动态模型选择的模型大小

图6报告了基于单个TVP-FAVAR模型估计的FCI以及经多个TVP-FAVAR模型动态选择和平均得到的DMA-FCI。可以发现,FCI和DMA-FCI的走势高度一致,数值上虽时高时低,但DMA-FCI要比FCI更平滑,尤其是在每轮金融周期的峰点和谷点处。这也是DMS和DMA的优势,每个样本点依概率选择重要的变量用于提取FCI,避免不重要的变量夸大金融状况的紧缩或宽松程度。

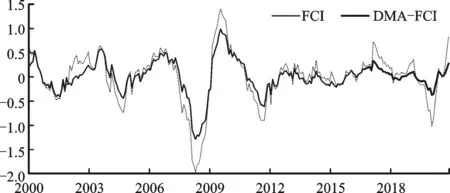
图6 FCI与DMA-FCI的走势

以“峰—峰”作为一轮周期的判定标准,图6报告的中国金融状况指数经历了六轮完整的周期。中国金融状况指数的周期长度稳定在3～4年之间,这与邓创等利用主成分分析法测度得到的结论相一致[14]。各金融领域波动相互叠加,终将反映到FCI的波动上来。本文以识别2000年以来中国重大金融事件为标准来判断DMA-FCI的合理性。

2000年7月以来,中国M1增速从局部高峰22.6%逐渐下探至2002年1月的9.5%,紧缩的货币政策下金融市场状况也跟着收紧,表现为DMA-FCI从2000年4月的0.54降为2001年7月的0.41,金融状况从宽松走向了紧缩。2001年中国加入世界贸易组织前后,对未来金融市场发展持不确定性观点使中国金融状况保持在较低状态。2002—2004年,DMA-FCI从零附近开始缓慢上升而后又逐渐下降,在此期间,中国M1和M2增速均保持在15%～20%的高速增长阶段,DMA-FCI与货币供应量呈现出相似的周期趋势,中国货币政策由稳健到适度宽松再回归稳健,对应的物价水平也是温和的、波动幅度小于2%。

2005年中国启动了股权分置改革,推动中国金融市场向好向上发展,金融状况指数逐渐上升。2007年左右,随着股权分置改革的完成,大批企业完成了上市,加之住房价格飙升、房地产投资热潮涌动,以及人民币一路升值带来大量外部资金涌入国内,中国金融市场处于繁荣状态,此时的金融状况指数到达局部峰值状态。与此同时,全球资本市场流动强盛,不同金融部门驱动作用的相互叠加使得中国物价水平上涨,进入严重的通胀期。2008年雷曼兄弟倒闭、资产泡沫迅速破灭,中国金融状况也急剧恶化,DMA-FCI于2008年6月下探至谷点-1.29,这也是2000年以来的历史最低点。金融危机还导致中国GDP增速明显放缓,物价水平急剧下跌,通胀率在2009年7月下探至-2.07%,进入了短暂的通缩期。

2008年下半年开始,为降低国际金融危机的破坏性影响,中国宏观调控当局迅速采取了适度宽松的货币政策和积极的财政政策,极力复苏中国经济,防止经济增速过快下滑。具体应对措施为“一揽子计划”,最重要的一项便是加大政府财政支出的同时减少税收,减轻企业负担。“4万亿计划”安抚了人心,成效凸显。具体表现为:中国货币供应量和信贷量增速加快,进而金融市场压力逐渐减小,DMA-FCI逐渐回升并于2009年8月达到2000年以来的最高点。此后,中国DMA-FCI又逐渐回落、缓慢向均值零靠拢,而后又受欧元贬值、人民币升值的影响在2011年9月下降至-0.61的局部谷点。2012年以来,中国经济发展进入“新常态”,金融状况指数在零附近上下波动,波幅较小,直到2015年中,中国金融市场受“股灾”的影响,金融状况指数保持在-0.21左右的局部谷点状态。2020开年以来受“新冠肺炎疫情”的影响,停工停产的大环境下中国经济景气状态达到2000年以来的历史最低,不景气程度甚于国际金融危机期间,进而金融状况也进一步恶化,DMA-FCI下探至2012年以来的局部低谷-0.35。

由此可见,本文构建的DMA-FCI可以识别出21世纪以来中国金融市场的重大风险事件,六轮周期中的谷点分别对应2001年加入世贸组织、2005年股权分置改革、2008年国际金融危机、2011年欧洲债务危机、2015年“股灾”与2020年“新冠肺炎疫情”。因此,动态模型平均测度的DMA-FCI可以描述样本期间中国金融市场环境的变化趋势,刻画了中国2000年以来的金融形势,是一个具有风险识别能力的FCI。

(四)金融状况指数的评估

下面通过递归预测来评估FCI对目标宏观经济变量的预测能力,预测评估期为2010M01—2020M11,预测步长为h=1,2,3,4,也就是向前预测1～4个月。通过计算均方预测误差(MSFE)来评估各模型的预测能力,将MSFE除以基准模型产生的相应值来对结果进行归一化,以便比较各模型的预测准确程度。

本文将不含FCI的VAR模型作为基准模型,基准模型记录的MSFE为真实值,而其他模型的MSFE则是与基准模型的相对值。TVP-FAVAR表示应用所有18个变量提取的FCI,TVP-FAVAR-DMS(DMA)表示在剩余13个变量中应用DMS和DMA提取的FCI。紧跟模型名称后面的参数c1和c2分别代表模型的延迟因子和遗忘因子,即κ1=κ2=c1且κ3=κ4=c2。除VAR模型是不包含FCI的二元模型外,其他模型是包含不同FCI的三元增强VAR模型。

表4报告了VAR类和FAVAR类模型对通胀和宏观经济景气一致指数的均方预测误差。对通胀来说,TVP-VAR、FAVAR及TVP-FAVAR模型的预测效果优于基准模型;而对宏观经济景气一致指数来说,只有包含FCI的FAVAR类和TVP-FAVAR类模型的预测效果要优于基准VAR模型。这说明,允许预测模型的参数随时间变化以及加入金融状况信息确实提高了对目标宏观经济变量的预测能力,因为经济结构具有不稳定性,况且FCI包含了有关经济活动的预期信息。此外,当向前预测2～4个月时,DMA和BMA模型分别是通胀和宏观经济景气一致指数的最佳预测模型。也就是,模型平均确实降低了风险,使预测结果趋于稳定,DMA-FCI能提高目标经济变量的预测能力。

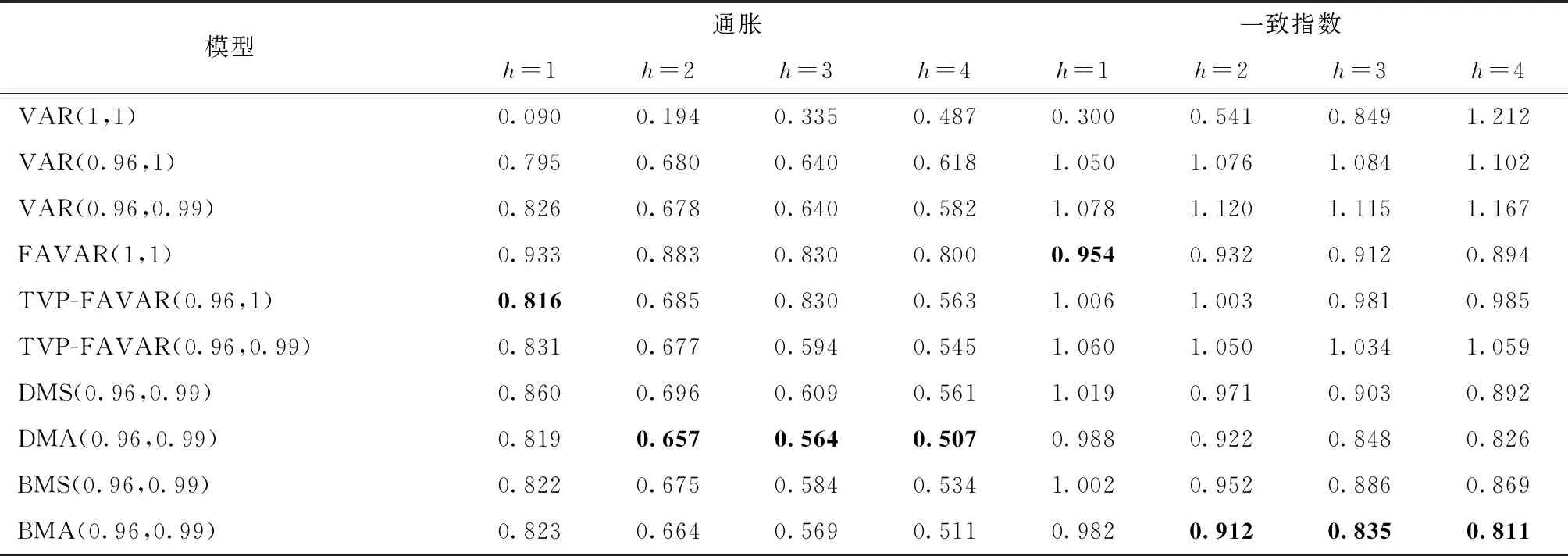
表4 均方预测误差(MSFE)

因此,在TVP-FAVAR模型采用DMA技术估计的FCI要比单个TVP-FAVAR模型估计的FCI的预测能力强。也就是说,DMA-FCI是本文测度结果中最佳的金融状况指数,因为它的预测能力最强,在TVP-FAVAR模型中执行DMA提取的FCI能显著提高宏观经济变量的预测能力。

五、结论

本文的目标是构建一个尽可能准确地预测通胀和经济状况的金融状况指数。为此,本文通过查阅大量国内外有关FCI的文献,并从FCI的变量选择、模型或方法的构建以及应用三方面进行归纳与总结,通过在TVP-FAVAR模型中始终固定5个典型的FCI的构成变量,并且对剩余的13个金融变量(缺口)执行动态模型选择和动态模型平均,最后构建了中国2000年1月至2020年11月期间的FCI。研究结果如下:

第一,金融状况指数(FCI)的测度结果表明,使用所有18个实际金融变量(缺口)在单个TVP-FAVAR模型中提取的FCI、基于动态因子模型提取的FCI以及采用主成分分析提取第一主成分得到的FCI是极其相似的。在多个TVP-FAVAR模型中执行动态模型平均测度的FCI虽与单个TVP-FAVAR模型提取的FCI很相似,但动态模型平均构造的FCI在峰点和谷点较为平滑。动态模型平均构造的FCI与中国通胀率和宏观经济景气一致指数的走势大体吻合,并且领先于通货膨胀率大约1年,领先于宏观经济景气一致指数大约3～6个月,并且其走势也与中国样本期内的金融形势变化大体一致,不管是周期特征,亦或是识别重大金融风险事件的能力,都有一定的合理性。

第二,金融状况指数(FCI)对目标宏观经济变量的预测结果表明,FCI对通货膨胀率和宏观经济景气一致指数的预测是有用的,FCI能提高宏观经济变量的预测性能。对于通胀来说,在向前1～4个月的预测中,所有模型的表现均优于基准VAR模型,但加入FCI的FAVAR或TVP-FAVAR模型表现更佳,特别是执行动态模型平均构造的FCI,其表现是最鲁棒的。对于宏观经济景气一致指数来说,TVP-VAR并没有基准VAR表现得好,反而是加入FCI后的FAVAR类和TVP-FAVAR类模型能改善宏观经济景气一致指数的预测性能;同样地,执行动态模型平均构造的FCI对宏观经济景气一致指数的预测能力是最强的。因此,在TVP-FAVAR模型中执行动态模型选择和动态模型平均可以改善对宏观变量的预测能力,该方法所构建的FCI是一个反映中国物价水平未来变化的晴雨表。