爆破P波作用下直埋压力管道安全振速研究

朱 斌，蒋 楠，周传波，贾永胜，吴廷尧

1) 中国地质大学(武汉)工程学院, 武汉 430074 2) 江汉大学爆破工程湖北省重点实验室, 武汉 430024 3) 武汉爆破有限公司, 武汉 430023

压力薄壁管道运输因其成本低、建设快、运输量大等特点广泛应用于各国城市居民的生产、生活等领域.随着21世纪地下空间时代的来临，大量新兴的地下空间工程的建设与现役埋地压力管道的矛盾不断涌现，爆破作为工程岩土体开挖的重要方式，其产生的地震有害效应对压力管道的影响尤为突出.如燃气压力管道在遭遇破坏后极易发生燃气泄露，造成严重的二次破坏导致生命财产的巨大损失.因此，研究工程开挖爆破地震作用下压力管道的振动破坏效应对于指导临近管道爆破施工安全生产，以及压力管道在爆破振动等不利因素影响下的安全设计具有重要意义.

目前国内外相关学者针对爆破地震作用下管道的安全性方面做了大量探索性研究[1-6]，实验方面，钟冬望等[7]与龚相超等[8]通过埋地钢管现场爆破，研究了埋地压力管道在实验条件下的应变峰值与爆心距和药量拟合关系；Mokhtari与Alavi Nia[9-10]通过埋地钢管爆炸响应实验，寻找管道爆炸安全距离.理论方面，刘优平等[11]以及王铁成和王卉[12]采用复变函数法研究了地下输流管道在平面P波作用下的动应力集中问题.Ghaznavi与Oskouei[13]研究了纵波传播方法对管道非线性应变量的影响.

上述研究中针对带压的薄壁管道研究相对较少，针对爆破地震波作用下薄壁压力管道的应力解析方法鲜有涉及.实际工程中，临近压力管道爆破工程中管道的内压对于管道振动时的应力大小具有不可忽略的影响，研究带压运行管道在爆破地震波作用下的安全性显得尤为重要[14].基于此，本研究根据内压薄壁圆筒受力特点，结合爆破地震波P波作用理论，采用静力分析和叠加原理建立爆破地震波作用下压力燃气管道动应力计算模型，并结合强度屈服准则对管道安全控制振速进行了解析计算，相关结论可以为破振动作用下薄壁压力管道的安全性和抗震设计提供依据.

1 P波入射对埋地压力管道作用特征

1.1 埋地压力管道受荷分析

当压力燃气管道邻近爆源进行爆破时，管道主要承受运行内压和爆破产生的地震动荷载作用，如图1（a）所示，图中p为管道运行内压.管道运行内压主要由管道运输燃气产生，由于天然气体密度小、无黏性，在研究其对管道的影响时，可以将其等效为沿管道内壁的均布荷载，大小为埋地管道运行压力设定值.管道所受爆破动荷载较为复杂，其作用特点与爆源特征、距离、岩土介质相关，在分析时根据研究特点做相关简化.大量工程实际研究表明[15-16]，爆破工程邻近管道爆破荷载由柱状装药的炮孔起爆产生，受影响管道大都处于爆破中区（Middle zone）、远区（Far zone）范围.根据柱状装药起爆产生的爆破地震荷载特征，爆破近区柱面P波、S波为主要成分，爆破远区平面P波为主要成分，P波传播速度较S波传播波速度快，其主要引起介质质点的水平向振动.在进行管道爆破动应力计算时，主要考虑爆破地震波平面P波入射时对管道应力状态的影响.

图1 压力管道邻近爆破荷载特征示意图.（a）压力管道附近的爆破地震波；（b）燃气管道荷载示意Fig.1 Characteristics of the pressure pipe near the blast: (a) blasting near the pressure pipe; (b) load on the gas pipe

爆破发生后，爆破荷载作为外加动荷载经过岩土介质传播施加到管道上，开始改变管道初始应力状态.由于P波传播速度较快，其波阵面首先到达管道迎爆侧，因此此时管道同时受到内压和爆破地震波P波动荷载作用，如图1（b）所示.薄壁压力管道在受到爆破地震荷载作用时，其荷载作用路径为，先受静内压力再受爆破振动荷载.由于内压荷载始终恒定不变，爆破地震波动荷载在达到振动峰值后具有随时间波动衰减的特性.在爆破地震波能量达到峰值时，介质的振动与应力均达到峰值，处于最危险状态.因此根据上述荷载特征，在进行管道应力分析时，可以根据初始应力状态将地震波作用的动态过程近似用振动峰值的最不利状态进行静力等效计算分析.

1.2 平面P波入射下管-土界面作用分析

根据平面P波在弹性介质中的传播特点，爆破工程产生的平面P波经岩土介质传播给管道.由于管-土介质之间存在紧密接触的不连续界面，当P波经过管-土界面时会产生反射、折射现象，如图2所示.当一束平面简谐P波以入射角度θ0经过管-土界面时会产生反射P波，反射SV波，折射P波，折射SV波，入射波与反射波和折射波同在XZ平面内，各波与平面法线方向所呈角度为θn，波的幅值为An，n=0，1，2，3，4 时分别表示入射P波，反射P波、反射SV波、折射P波和折射SV波.由于薄壁管道也具有一定厚度，且燃气管道输送燃气密度大、无黏性，因此管道内表面可等效看作自由界面，此时透过管-土界面的折射P波、折射SV波会在管道内壁再次生成反射P波和反射SV波，如图2所示.图中，λ、μ为土层介质的拉梅常数；e为土层介质泊松比；λ′、μ′为管道介质的拉梅常数，e′为管道介质泊松比.

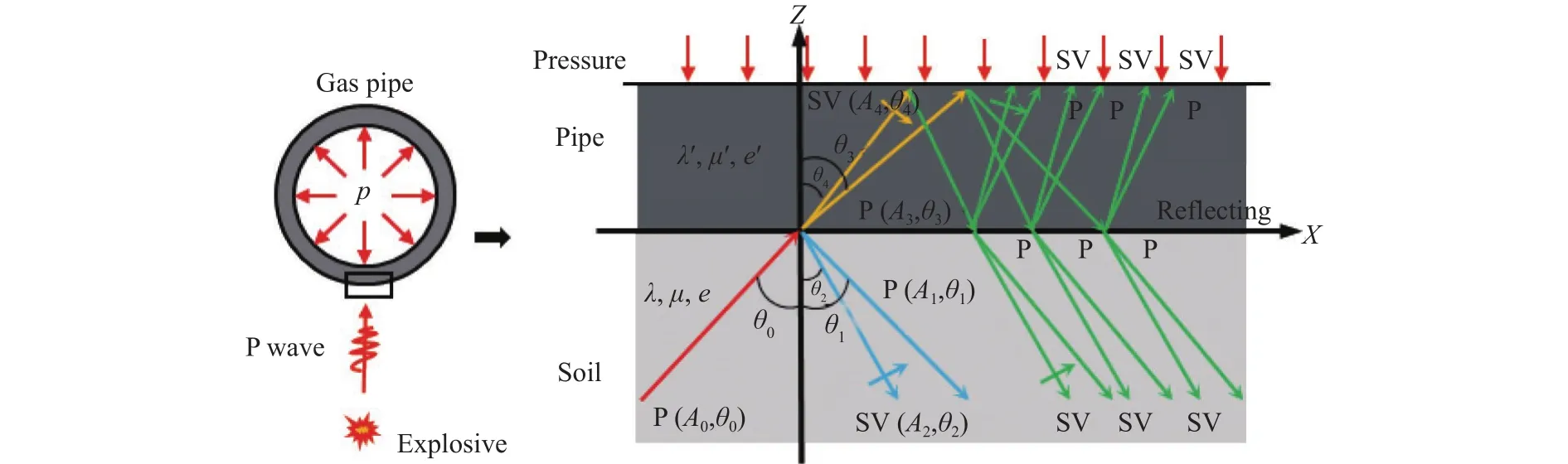
图2 平面P波入射管-土界面示意图Fig.2 Schematic diagram of the planar P wave incident to the tube-soil interface

根据周俊汝等[17]、以及陈明与卢文波[18]的研究，由于入射波实际上是个无限宽的波束，因此在厚度介质中的同一点将同时有许多个波的作用.管道厚度一般在10～20 mm左右，爆破振动主频率在10～300 Hz内.此时应力波的相长干涉较小，假设可以忽略不计.文献中计算表明，在考虑多次反射波的作用条件下，不管以何大小的入射角入射一定厚度介质时，其在介质内部以及介质结合界面处的应力都会减小.这说明，考虑应力波多次折射、反射的合作用产生的应力远远小于考虑单次折射波作用的应力.上述研究表明，折射波在介质内产生的反射波将降低介质应力.因此，研究爆炸应力波作用下薄壁管道的破坏可以忽略管道内壁自由界面的影响，仅考虑其通过管-土界面时的作用特征.

2 平面P波作用下压力管道动应力解析

2.1 假设条件与计算模型

根据上述埋地压力管道在爆破作用下的受荷特征分析，基于弹塑性力学、平面波动理论对管道计算模型做出如下简化假设：（1）压力管道、岩土介质为均质弹性介质；（2）管道厚度均匀，管道轴向两端为自由约束；（3）管道内压沿壁厚均匀分布，入射P波为一维平面简谐波不考虑体力影响.由于管道内压恒定，当爆破能量达到峰值时，管道内压与峰值地震波动荷载作用下近似看作拟静力状态，其单元加载如图3（a）所示，管-土界面单元在不同状态下的受力状态如图3所示，图中各波产生的位移为Un，n=0，1，2，3，4 时分别表示入射P波，反射P波、反射SV波、折射P波和折射SV波，σr和σθ表示初始压力作用下管道单元的镜像和环向应力，σZ和σX表示爆破地震P波入射后管道在ZX平面产生的沿Z和X方向的峰值动应力.

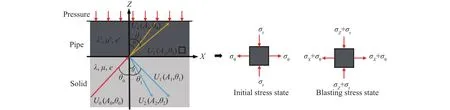
图3 管-土界面位移及单元应力模型Fig.3 Pipe-soil interface displacement and element stress model

2.2 压力薄壁管道初始应力

根据上述管道受力过程以及计算模型分析，当爆破振动产生前，根据薄壁压力容器受力特点，薄壁燃气管道仅受均匀内压作用，处于受力平衡状态.当管道两端自由且看作无限长时，管道截面处于平面应力状态，具有均匀的初始径向应力σr、环向应力σθ，如图3所示，根据薄壁压力管道理论[19]计算管道单元应力如式（1）所示.

其中，σθ为环向应力，MPa；σr为初始径向应力，MPa；p为管道运行内压，MPa；D为管道内径，mm；δ为管道有效壁厚，mm.根据式（1）分析，当埋地压力管道仅受均匀内压时，管道平面产生径向和环向应力，均与内压大小呈正相关关系，且管道切向应力还受管道尺寸壁厚和直径影响.

2.3 管-土界面爆破地震动应力、位移解析

根据平面波动理论，利用波的位移函数来分析，其中平面简谐波在介质中传播产生的位移Un可以由式（2）表示.

其中，An为波的振幅，m；ω为频率，Hz；cn为波在介质中的传播速度（n=0，1，2,···,4），m·s-1.根据图3可知，管-土界面两端由波传播产生的位移由式（3）计算.

其中，un为法向位移，upipe为管道端法向位移，usoil为土层端法向位移，vn为切向位移，vpipe为管道端法向位移，vsoil为土层端法向位移（n=0，1，2，3，4），根据式（2）、（3）得到管-土界面两侧切向、法向合位移表示如式（4）所示.

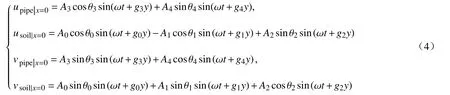
根据虎克定律可知，波在介质中传播时位移与应力的关系由式（5）计算[14].

其中，σZ为正应力，MPa；σX为切应力，MPa；E为介质弹性模量.根据式（2）～（5），管-土界面两端应力如式（6）所示.

根据反射、折射定律，在介质界面处，入射角、折射角、反射角和波在介质中的传播速度cn之间具有相关关系，如式（7）所示.

其中，kn为波在各介质中的透反射角度比；c为波速常数，m·s-1.

此外，由于爆炸应力波是多频率成分叠加而成的复杂组合，因而任何单一的波形都无法代表爆破震动的传播特征.选取统计意义上的、贡献最大的频率成分作为考察对象，可把爆炸应力波视为简谐波，则质点峰值振动速度Vn、主频率ω与最大振幅Anmax之间的关系如式（8）[20]所示.

根据相关研究，平面P波入射界面上产生的反射和折射波振幅之间具有相关关系，由此可以定义波的振幅比Kn（n=0，1，2，3）的计算式如式（9）所示.

综合式（6）～（9），当P波入射使管-土界面两侧振幅达到最大值时，管-土界面两侧峰值动应力可以由式(10)表示.

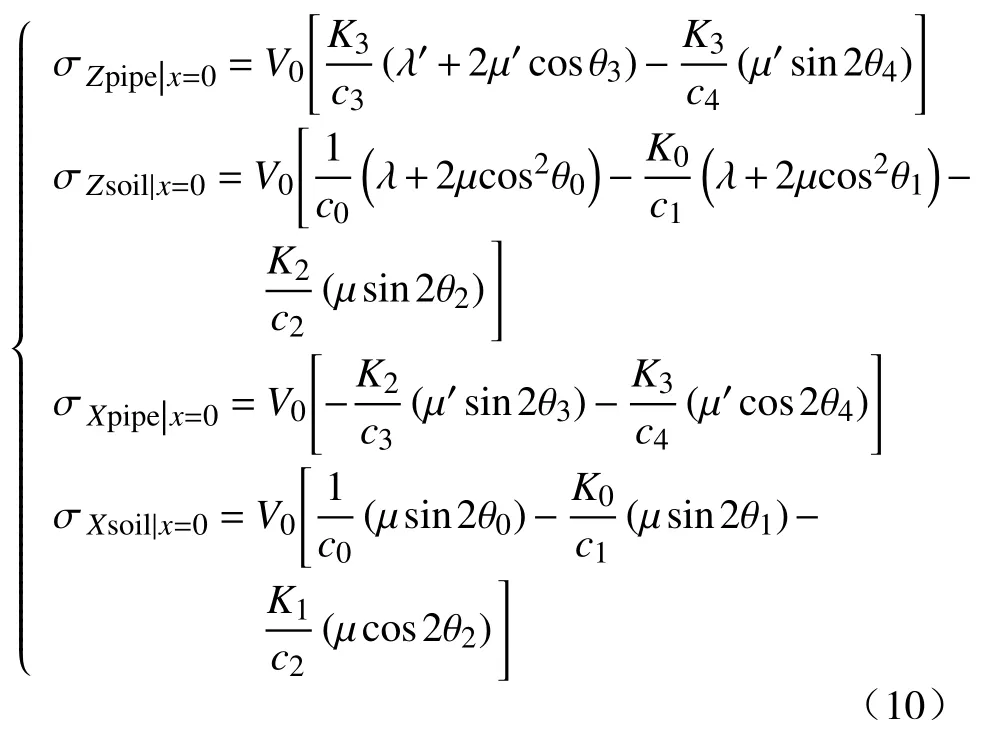
根据式（10），在求得各透、反射波位移幅值比Kn的情况下，对于给定的入射峰值振动速度V0，可以很容易求得管-土结合面两侧的法向、切向应力值.且根据式（10）分析可知，管-土两侧由P波入射产生的介质应力大小与介质性质参数相关，当介质材料性质一定时，管-土界面两侧应力大小由入射波的峰值振速和入射角度决定.

3 压力管道爆破振动应力与安全振速分析

3.1 管-土界面应力特征与强度准则

根据管-土界面特点分析可知，大多数埋地管道为刚度较大，强度较高的金属管道，主要发生以材料屈服为主的拉伸或弯曲破坏[21]；而管周填土大多为刚度较小，强度小的软黏性土等，主要发生剪切破坏[22].由于两种介质的强度、刚度差异，认为管-土界面作用主要为静摩擦力而非混凝土衬砌等结构的胶结力.根据上述分析，假设管-土界面为连续界面，因此爆破振动时管道随土壤一起运动，根据界面位移、应力连续条件，在界面处应满足式（11）.

其中，σZpipe、σXpipe为管-土界面管道侧的正应力、切应力，σZsoil、σXsoil为土壤侧正应力、切应力；根据式（11）可知，由于管道强度远大于土壤强度，当爆破振动产生的管-土界面应力大于界面滑动摩擦力或者使土壤发生剪切、拉伸破坏时，管道材料并不会发生破坏，管道仍然具有使用强度.因此，实际工程中，针对埋地管道的安全评价往往以管道本体的破坏为依据.根据图3可知，爆破振动荷载加载时压力管道侧单元的受力应由初始应力和爆破峰值应力叠加产生，其计算式如式（12）所示.

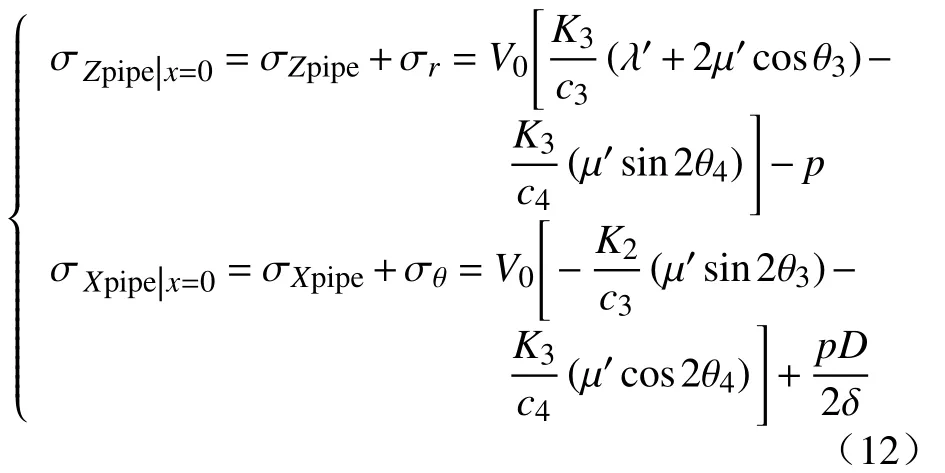
根据材料力学相关理论，针对燃气管道常用球墨铸铁、碳钢等金属材料，其变形阶段会经过弹性阶段、屈服阶段、强化阶段和紧缩阶段，当应力超过弹性极限时材料就会进入屈服，当应力超过材料屈服极限时认为管道材料失效.根据上述分析，管道界面处于平面应力状态，采用Tresca屈服条件进行判定，该理论认为金属的塑性变形是由剪应力引起金属中晶格滑移而形成的，当最大剪应力达到某一极限值时材料进入塑性状态，其判别式如式（13）所示[23].

其中，σe为有效应力，MPa；σs为材料屈服强度，MPa；η为压力管道设计安全系数；σ1、σ3为主应力，MPa.由于管道单元处于平面应力状态，因此分别对应压力管道侧轴向、切向应力.结合式（13），可以得到压力管道爆破振动有效应力安全判别式如式（14）所示，根据式（14）可以推导求出P波作用下压力管道的安全振速表达式如式（15）所示.

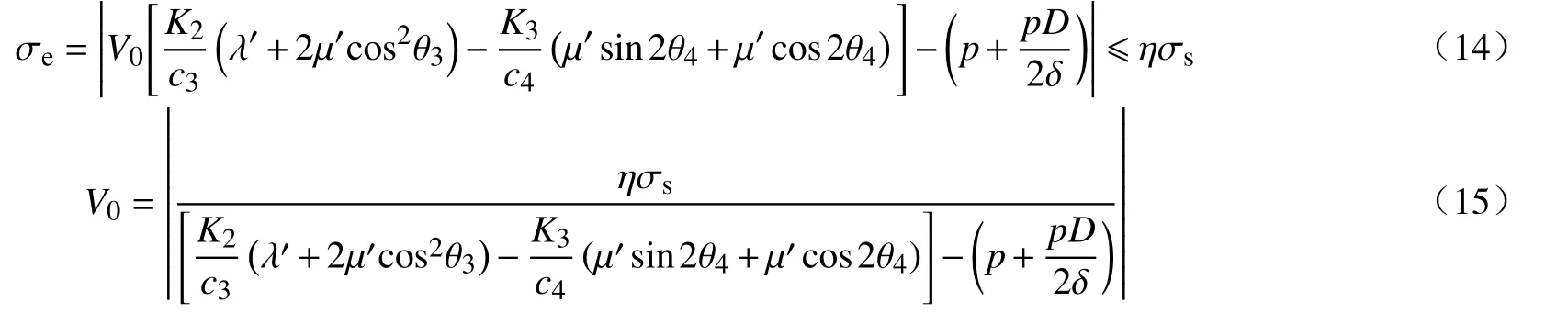
根据《输气管道工程设计规范》（GB50251—2015）[24]可知，城市埋地燃气管道的地区等级按照四级算，管道强度设计系数η可取0.3.根据上式（15），在已知入射波相关参数的情况下即可计算管道材料此时峰值有效应力的大小，根据安全判别式即可对管道安全状态做出判定.

3.2 计算实例与结果分析

为进一步分析研究爆破地震波作用下埋地压力管道的应力和安全振速，根据相关研究，采用如下两个具有代表性的管道邻近爆破振动实例进行研究.

实例1：全尺寸下穿燃气管道爆破试验[1]，实验燃气管道运行内压为0 MPa，为球墨铸铁管道DN 1000，直径为 1000 mm，壁厚δ1=10 mm，材料密度ρ1′=7.89 g·cm-3，泊松比μ1′=0.3，屈服强度σs′=300 MPa，弹性模量E1′=195 GPa.管道埋置土层为粉质黏土层，土层密度ρ1=1.89 g·cm-3，泊松比μ1=0.35，弹性模量E1=0.089 GPa.

实例2：爆破荷载作用下埋地钢管动态响应实验[4-5]，实验管道运行内压为0.6 MPa，管道材料为无缝钢管 Φ300，壁厚δ2=4.4 mm，材料密度ρ2′=7.9 g·cm-3，泊松比μ2′=0.3，屈服强度σs′=282 MPa，弹性模量E2′=210 GPa.管道埋置土层为高饱和黏性土，土层密度ρ2=1.78 g·cm-3，泊松比μ1=0.33，弹性模量E1=0.059 GPa.

根据波在介质中的传播特点，介质中纵波和横波的传播速度可按照式（16）计算[25]：

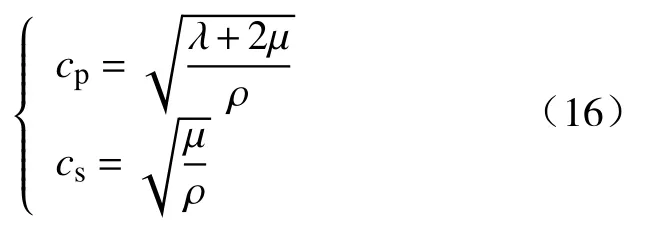
其中，cp为介质中纵波波速，m·s-1；cs为介质中横波波速，m·s-1.根据式（16）将实例中管道和土壤相关参数带入计算可得波在介质中的传播速度，计算结果如表1所示.

表1 计算实例介质波速和临界角计算Table 1 Calculation examples’ media wave velocity and critical angle calculation

根据上述计算结果可知，当波从土壤经管-土界面传播给管道介质时，由于cpipe＞csoil因此当入射波的入射角增大时，存在某一临界入射角使折射角度为90°时发生全反射，其中根据波的折射规律，入射波临界入射角的计算式如式（17）所示.

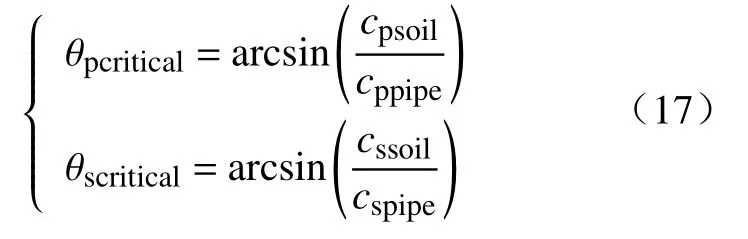
结合公式（15）、（16），根据岩层和管道相关参数，计算可得实例1、实例2中的横波、纵波临界入射角度θpcritical、θscritical如表1所示.

根据上述实例计算结果可知，当平面P波经土壤入射到管-土界面时，实例1、2中的入射波入射角大于1.27°、1.13°时在管-土界面产生全反射，当发生全反射时，入射波在管-土界面产生透射滑行P、SV波，因此管道一侧仅有沿界面的剪切应力，假设滑行波的振动幅值仍满足式（9）.则结合式（14）计算实例1、2中爆破振动作用下管道安全振速随入射角度的变化如表2所示.

表2 不同入射角下的管道安全振速Table 2 Safe vibration velocity of the pipeline under different incident angles

根据表2中的计算结果分析可知，当P波垂直入射时（θ0=0°），管道有效应力值较大，安全振速最小.当入射波达到临界角度发生全反射时，界面滑行波所占能量较小，产生的切向应力较小，因此安全振速较大，且随着角度的增大而增大.由上述分析可知，在进行地震波入射下压力管道的安全计算时主要考虑垂直入射情况，因此上述实例中满足实验工况下计算参数时，管道的安全振速分别为9.24 cm·s-1和7.62 cm·s-1.为进一步分析压力对管道有效应力与安全因素的影响，根据式 (14)分析可知，管道运行压力直接影响管道爆破振动有效应力的大小，根据我国《城镇燃气设计规范》（GB50028—2006）[26]中运行内压的大小规定，依次按照低压（0 MPa、0.2 MPa），中压（0.4 MPa），次高压（0.6 MPa、1 MPa）和高压（1.2 MPa）对上述实例1、2中管道的安全振速进行计算分析，如图4所示.

图4 不同运行压力下管道安全振速.（a）计算实例1；（b）计算实例2Fig.4 Safe vibration speed of the pipeline under different operating pressures: (a) Example 1; (b) Example 2

根据图4分析可知，运行压力对安全振速影响较大，管道计算安全振速随着运行压力的增大减小，说明管道内压对管道爆破振动安全的影响是不利的.且当入射角度为0°时其安全振速最小，对比爆破安全规程[27]中其他建构筑物的爆破振动安全控制值，均在同一量级内计算合理.此外随着入射角度的增加，入射波发生全反射.透射波能量急剧减小，因此安全振速也急剧增大，其量级远大于爆破安全规程中的其他值，因此不建议采用.综上所述，本研究适用于计算爆炸中、远区的直埋薄壁压力管道的安全振速，计算过程中不考虑管道因腐蚀和接口产生的其他应力，在进行管道爆破振动安全评估时应根据现场管道运行压力的特点，选择计算结果中的较小值作为安全控制值.

4 结论

根据受均匀内压薄壁圆筒受力理论，结合P波作用下均匀弹性介质内的应力计算，采用拟静力叠加状态对爆破地震波作用下直埋压力燃气管道应力进行了计算分析，得到如下结论.

（1）根据受力分析，爆破荷载施加前管道仅受均匀内压，管道具有初始轴向和切向应力；爆破发生后，管道同时受到内压和爆破地震波P波动荷载作用，在进行管道应力分析时，可以根据初始应力状态将地震波作用的动态过程近似用振动峰值的最不利状态进行静力等效计算分析.

（2）管道初始应力受内压和管道直径、壁厚影响，管道动应力则主要由土层中入射到管道单元中得折射波产生，压力管道爆破振动峰值应力与入射波的振动幅值、频率入射角度相关；在进行安全校核时，由于管、土介质的强度、刚度差异较大，以管-土界面管道一侧强度作为安全判据较为合理.

（3）管-土界面入射波临界角较小，管道峰值应力随入射角度增大而减小，垂直入射时主要发生拉伸破坏，发生全反射时发生切向破坏；压力管道安全控制振速随入射角的增大而增大，随运行内压的增大而减小，实际工程中根据管道内压实际情况，选择较小值作为安全控制值.