模糊层次分析法在我国深空探测方案优选应用探究

刘彤杰，宋洪庆，张 杰，骆笑天，彭如意，张贤国4,

1) 北京航空航天大学宇航学院，北京 102206 2) 上海航天技术研究院，上海 201109 3) 北京科技大学土木与资源工程学院，北京 100083 4) 北京科技大学深空探测与资源识别利用联合实验室，北京 100083 5) 中国科学院国家空间科学中心，北京 100190

深空探测是人类走出地球，探知地外世界的重要途径，对认识宇宙起源、行星组成及其演化、人类生存空间的扩展和地外生命的探索具有重要的意义[1-4].中国深空探测起步于月球探测，按照探月工程“绕、落、回”三步走的任务规划[5-9]，自2004年探月工程一期启动以来，已成功实施了5次探测任务，我国探月工程五战五捷[10-11]，实现人类首次在月球背面软着陆和巡视探测以及我国首次对地外天体进行无人自动采样和返回等探月领域的重大突破，我国已迅速跻身于国际月球探测先进行列[12-19].这些成功离不开严谨科学的方案编制和决策机制.

深空探测工程是复杂的系统工程，每一项要素都受其他要素直接或间接制约，各个要素之间的重要性互相制约，很难平衡.同时需要多技术领域、多学科专业队伍的协同配合，需要综合集成密集的复杂新技术、有效配置从研制生产到试验验证各环节的资源保障、准确识别和科学应对大量不确定性风险，还应注重科学与技术并举、协同发展推进.以中国探月工程为例，在方案决策过程中，经论证组论证和中介机构专家评估后形成的方案，人为影响比较明显，工程总体很难快速做出科学决策.因此，运用科学的方法进行决策在深空探测领域至关重要.许多学者针对深空探测中涉及学科领域多、工程复杂、可选方案多和总体设计方案优选难度大等问题，提出人工智能方法和改进专家权重调整算法等方法提高最优方案的科学性和决策的可信性[20-21].

层次分析法以及在层次分析法基础上建立的模糊层次分析法是一种实用的多因素多目标决策方法，在许多领域都发挥着作用.针对层次分析法所具有的检验判断矩阵是否具有一致性非常困难等问题，引进了模糊一致矩阵的概念，进而产生了模糊层次分析法[22].深空探测工程的发展目标的评价与优选是一个难以定量的多因素决策问题，适合采用层次分析法和模糊层次分析法等综合评价方法进行决策和优选.朱毅麟[23]，以及Higgins和Benaroya[24]采用层次分析法进行最优月球环境配置等深空探测领域的研究.还有学者采用模糊层次分析法进行航天系统的安全风险管理以及航天测控任务方案的优选决策等问题研究[25-28].

模糊层次分析法相比于层次分析法具有更容易检验判断矩阵是否具有一致性的特点，但是在深空探测方案优选领域应用较少，因此本文引入模糊层次分析法，以中国探月工程为例，从多个方面考虑影响探月总体方案的因素，全面分析各因素指标，建立多层次系统指标评价模型，然后计算出各影响因素的权值，选择合适的模糊综合评价方法对各方案实现评价，最终得到探月总体方案中的最优方案.

1 模型建立

1.1 模糊层次分析法

层次分析法是由20世纪70年代由美国著名运筹学学家T.L.Saaty提出的[29].层次分析法考察影响决策的众多要素及其内在关系，对要素进行层次划分并构建层次结构模型，采用有限的定量信息对决策问题进行定量或者定性分析[30].层次分析法为多要素影响下的复杂决策问题提供科学有效的决策方法，现在已广泛地应用在企业管理决策、科研管理、工程方案确定等方面.

模糊层次分析法是在传统的层次分析方法基础上，考虑到人们对复杂事物判断的模糊性，引入模糊一致矩阵的决策方法.

1.1.1 模糊层次分析法原理

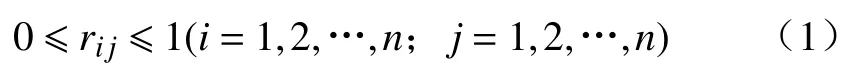
模糊互补矩阵R不仅是模糊矩阵，而且满足：

说明元素i和元素j相比较的重要性与元素j和元素i相比较的重要性正好互补.模糊一致矩阵R不仅是模糊互补矩阵，而且满足∀i,j,k有：

其中：rij=0.5，表示元素i和元素j同样重要；0＜rij＜0.5表示元素j比元素i重要，且rij越小,元素j比元素i越重要；0.5＜rij＜1表示元素i比元素j重要，且rij越大，元素i比元素j越重要.

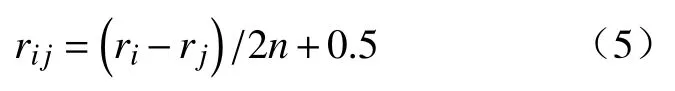
则变换以后的矩阵是模糊一致矩阵.从模糊一致矩阵R中划掉任意一行及其对应列所得的子矩阵仍然是模糊一致矩阵.模糊一致矩阵R满足中分传递性，即：

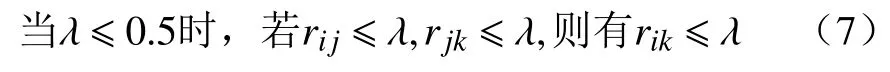
基于每一层次中的因素针对上层因素的相对重要性构建优先关系矩阵，通过由优先关系矩阵转换成的模糊一致判断矩阵的元素与权重的关系式求因素权重.因素Ai在目标Ok下的权重的计算公式[31]为：

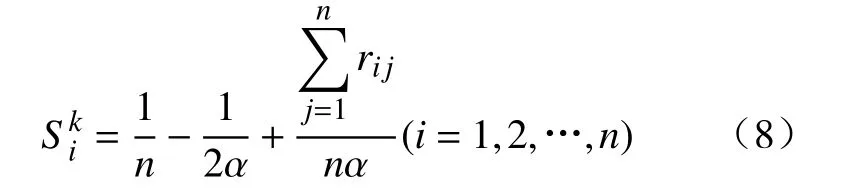
1.1.2 算法流程

模糊一致矩阵与人类决策思维具有相一致的特性，因此，基于模糊一致矩阵的模糊层次分析方法在评价指标较多、评价带有模糊性的方案优选中应用较多.模糊层次分析法一般需要经过建立优先关系矩阵、将优先关系矩阵转换成模糊一致矩阵、层次单排序、层次综合和层次总排序这五大步骤.图1为模糊层次分析法流程图.

图1 模糊层次分析法流程图Fig.1 Fuzzy analytic hierarchy process flow chart

在建立优先关系矩阵时，每一层次中的因素针对上层因素的相对重要性建立矩阵，本研究采用如表1所示的简单标度法（只有0、0.5和1三个数量标度）给予数量标度.

表1 简单标度法Table 1 Simple scale method

然后将各优先关系矩阵转换成模糊一致矩阵；之后进行层次单排序，根据模糊一致矩阵计算在上一层某目标下层次各因素的重要次序，采用模糊一致判断矩阵的元素与权重的关系式即因素Ai在目标Ok下的权重的计算公式（8）求因素权重.

当中间层为准则层、子准则层时,需要综合层次关系，将局部的层次间的重要性权值转化为相对于总目标的综合权重.最后在层次单排序和层次综合的基础上，计算各个方案相对于总目标的总体优度Ti的大小对各方案进行排序，就可得到方案从优到劣的次序，总体优度Ti的计算公式如（9）所示.

1.2 模型层次结构的确定

评价任务方案的优劣以方案的总效能为标准，所以评价体系的最终目标是方案效能.为了有助于建立正确的效能指标体系，有必要开发一种用于合理地确定系统效能指标体系的分析结构，因此层次化的指标体系一般可分为最高层、中间层和最低层三个层次.最高层只有一个元素，即问题要达到的目标，也称目标层.中间层为准则层，根据问题规模的大小及复杂程度，可以再分出子准则层（指标层）.最低层为方案层，包括为实现目标可供选择的方案.

根据系统工程管理要素和科学探索任务特点，建立中国探月工程方案优选层次结构如图2所示.中国探月工程方案优选层次结构由目标层（F层）、准则层（S层）、指标层（T层）和方案层（P层）四部分构成.其中目标层是探月总体方案，准则层项目是技术、科学、经费、周期和效益.技术对应的指标层项目是先进性、可靠性、资源需求、团队基础、体系规范和风险；科学对应的指标层项目是科学价值、研制难度、探测难度和研究难度；经费对应的指标层项目是研制费、条件保障、运行费、科学研究费和社会资本；周期对应的指标层项目是规划符合度和计划可行性；效益对应的指标层项目是科学产出、技术推动、社会影响、政治外交、人才培养和成果转化.

图2 层次结构图Fig.2 Hierarchical chart

以嫦娥四号为算例，方案层有四个方案，如表2所示.方案一是由俄罗斯联盟号运载火箭搭载发射（原来和印度合作探月任务，但印度退出合作.俄罗斯转而提出可以搭载我国中继星），用长征三号乙运载火箭发射着陆器和巡视器组合体；方案二是由长征二号丙运载火箭+SM固体上面级发射中继星，长征三号乙运载火箭发射着陆器和巡视器组合体；方案三是由长征四号丙运载火箭发射中继星，长征三号乙运载火箭发射着陆器和巡视器组合体；方案四是由长征五号运载火箭发射中继星及着陆器和巡视器组合体.

表2 嫦娥四号总体方案Table 2 Overall plan for CE-4

2 结果与讨论

2.1 判断矩阵的建立

在层次结构表的基础上邀请具有丰富探月工程方案决策经验的管理人员，以及技术、科学等领域专家进行计算参数赋值建立优先关系矩阵.第一层和第二层之间的矩阵为F-S，第二层和第三层之间的矩阵为S1-T、S2-T、S3-T、S4-T和S5-T，第三层和第四层之间的矩阵为T1-P、T2-P、T3-P、T4-P、T5-P、T6-P、T7-P、T8-P、T9-P、T10-P、T11-P、T12-P、T13-P、T14-P、T15-P、T16-P、T17-P、T18-P、T19-P、T20-P、T21-P、T22-P和 T23-P，共计 29个矩阵.

在S层中，与F层“探月总体方案”相关的因素是S1、S2、S3、S4和S5.所以F-S矩阵中是这五个因素的相对比较.邀请管理人员进行技术、科学等准则的重要性判断，得到F-S优先关系矩阵如表3所示.

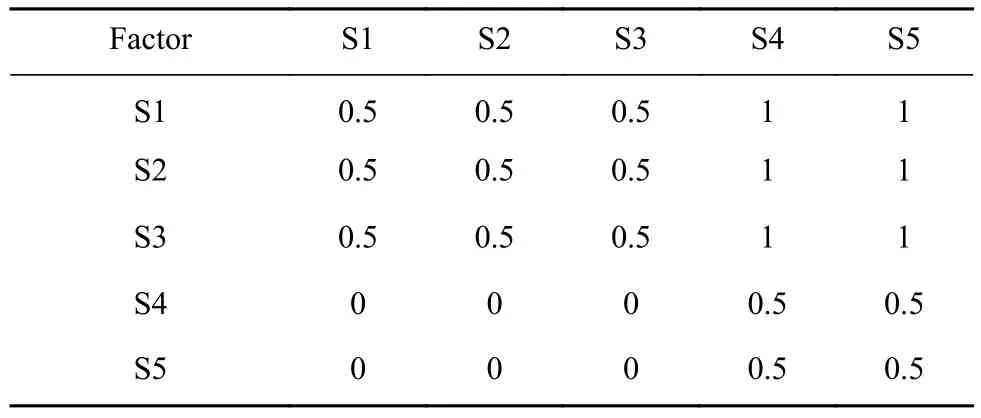
表3 F-S优先关系矩阵Table 3 F-S priority matrix

在T层中，与S层第1个因素“技术”相关的因素只有 T1、T2、T3、T4、T5和 T6，所以 S1-T矩阵中只有这六个因素的相对比较.邀请技术专家进行先进性和可靠性等指标的重要性判断，得到S1-T优先关系矩阵如表4所示.S2-T、S3-T、S4-T和S5-T类似S1-T矩阵，限于篇幅，不一一列出.

表4 S1-T优先关系矩阵Table 4 S1-T priority matrix

在P层中，与T层第1个因素“先进性”相关的因素是P1、P2、P3和P4.邀请技术专家针对先进性指标，基于“运载技术”和“探测器系统技术”两个方面，对四个方案的相对重要性进行比较，得到T1-P优先关系矩阵如表5所示.T2-P、T3-P、T4-P、T5-P、T6-P、T7-P、T8-P、T9-P、T10-P、T11-P、T12-P、T13-P、T14-P、T15-P、T16-P、T17-P、T18-P、T19-P、T20-P、T21-P、T22-P和 T23-P类似 T1-P矩阵，限于篇幅，不一一列出.

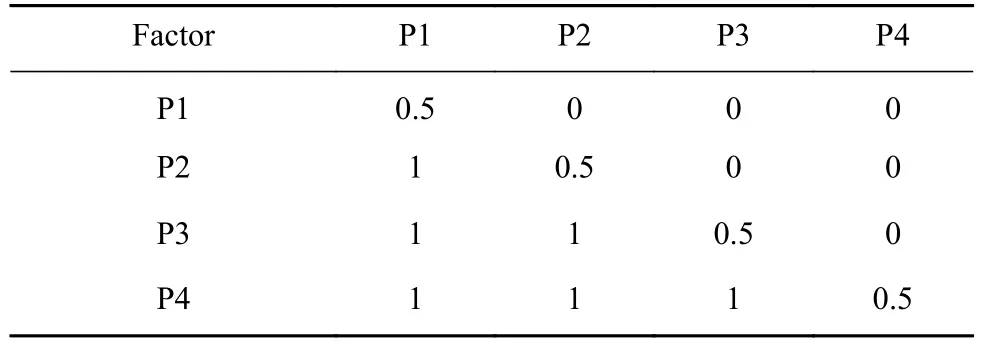
表5 T1-P优先关系矩阵Table 5 T1-P priority matrix

通过公式（4）将以上优先关系矩阵转换为模糊一致矩阵.

2.2 准则层因素权重

图3表示准则层各因素对目标层的权重.准则层相对于目标层，技术、科学和经费这三个因素所占权重相同，为0.25；周期和效益这两个因素所占权重相同，为0.125；技术、科学和经费这三大因素对探月总体方案而言同等重要，高于周期和效益这两大因素.

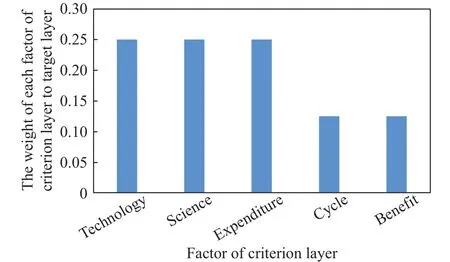
图3 准则层各因素对目标层的权重Fig.3 Weights of each factor of criterion layer to target layer

2.3 指标层因素权重

图4表示指标层各因素对准则层因素的权重.指标层中的因素相对于准则层的技术因素来说，先进性所占权重和可靠性相同，为0.233；资源需求、体系规范和风险所占权重相同，为0.117；先进性、可靠性所占权重大于团队基础，大于资源需求、体系规范和风险；先进性、可靠性这两大因素对于技术而言是最为重要的，其次是团队基础，再是资源需求、体系规范和风险.指标层中的因素相对于准则层的科学因素来说，研制难度和探测难度所占权重相同，为0.25；科学价值所占权重最大，为0.375；研究难度所占权重最小，为0.125；科学价值因素对于科学而言是最为重要的，其次是研制难度和探测难度，再是研究难度.指标层中的因素相对于准则层的经费因素来说，研制费所占权重最大，为0.3，其次是条件保障，为0.25，再是运行费，为0.2，再是科学研究费，为0.15，最后是社会资本，为0.1；研制费因素对于经费而言是最为重要的，其次是条件保障，再是运行费，再是科学研究费，最后是社会资本.指标层中的因素相对于准则层的周期因素来说，规划符合度和计划可行性所占比重相同，都为0.5；规划符合度和计划可行性对于周期而言是同等重要的.指标层中的因素相对于准则层的效益因素来说，科学产出和技术推动所占权重最大，为0.233，其次是社会影响和政治外交，为0.167，再是人才培养，为0.117，最后是成果转化，为0.083；科学产出和技术推动对效益而言是最为重要的，其次是社会影响和政治外交，再是人才培养，最后是成果转化.

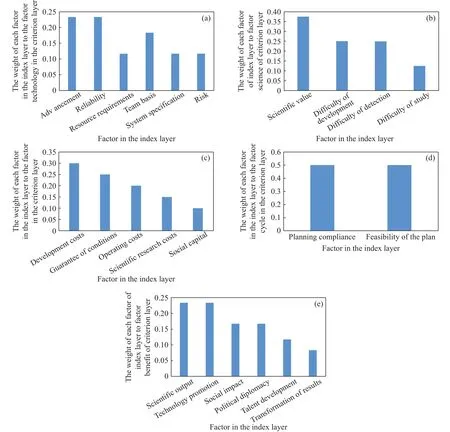
图4 指标层各因素对准则层因素的权重.(a) 技术; (b) 科学; (c) 经费; (d) 周期; (e) 效益Fig.4 Weights of each factor in the index layer to the factor in the criterion layer: (a) technology; (b) science; (c) expenditure; (d) cycle; (e) benefit

2.4 方案权重

2.4.1 技术指标分析

图5表示各方案对技术对应指标层各元素的权重.各方案相对于指标层的先进性因素来说，方案4所占权重最大，为0.375，其次是方案3，为0.292，再是方案 2，为 0.208，最后是方案 1，为 0.125；从先进性角度看，方案4是最优的，其次是方案3，再是方案2，最后是方案1.各方案相对于指标层的可靠性因素来说，方案3所占权重最大，为0.375，其次是方案 4，为 0.292，再是方案 2，为 0.208，最后是方案1，为0.125；从可靠性角度看，方案3是最优的，其次是方案4，再是方案2，最后是方案1.各方案相对于指标层的资源需求因素来说，方案1、方案2、方案3和方案4，都为0.25；从资源需求角度看，方案1、方案2、方案3和方案4是相同的.各方案相对于指标层的团队基础因素来说，方案4和方案3所占权重最大，为0.333，其次是方案 2，为 0.208，最后是方案 1，为 0.125；从团队基础角度看，方案4和方案3是最优的，其次是方案2，最后是方案1.各方案相对于指标层的体系规范因素来说，方案2、方案3和方案4所占权重相同，为0.292，高于方案1的0.125；从体系规范角度看，方案2、方案3和方案4是最优的，其次是方案1.各方案相对于指标层的风险因素来说，方案3所占权重最大，为0.375，其次是方案2，为0.292，再是方案 4，为 0.208，最后是方案 1，为 0.125；从风险角度看，方案3是最优的，其次是方案2，再是方案4，最后是方案1.

图5 各方案对技术对应指标层各元素的权重.(a) 先进性; (b) 可靠性; (c) 资源需求; (d) 团队基础; (e) 体系规范; (f) 风险; (g) 综合Fig.5 Weights of each scheme to each element of the corresponding index layer of technology: (a) advancement; (b) reliability; (c) resource requirements; (d) team basis; (e) system specification; (f) risk; (g) synthesis

2.4.2 科学指标分析

图6表示各方案对科学对应指标层各元素的权重.各方案相对于指标层的科学价值因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从科学价值角度看，方案1、方案2、方案3和方案4是相同的.各方案相对于指标层的研制难度因素来说，方案1、方案2和方案3所占权重相同，为0.292，高于方案4的0.125；从研制难度角度看，方案1、方案2和方案3是最优的，其次是方案4.各方案相对于指标层的探测难度因素来说，方案1、方案2和方案3所占权重相同，为0.292，高于方案4的0.125；从探测难度角度看，方案1、方案2和方案3是最优的，其次是方案4.各方案相对于指标层的研究难度因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从研究难度角度看，方案1、方案2、方案3和方案4是相同的.

图6 各方案对科学对应指标层各元素的权重Fig.6 Weights of each scheme to each element in the scientific corresponding index layer

2.4.3 经费指标分析

图7表示各方案对经费对应指标层各元素的权重.各方案相对于指标层的研制费因素来说，方案1所占权重最大，为0.375，其次是方案2和方案3，为0.25，最后是方案4，为0.125；从研制费角度看，方案1是最优的，其次是方案2和方案3，最后是方案4.各方案相对于指标层的条件保障因素来说，方案1和方案3所占权重最大，为0.333，其次是方案 2，为 0.208，最后是方案 4，为 0.125；从条件保障角度看，方案1和方案3是最优的，其次是方案2，最后是方案4.各方案相对于指标层的运行费因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从运行费角度看，方案1、方案2、方案3和方案4是相同的.各方案相对于指标层的科学研究费因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从科学研究费角度看，方案1、方案2、方案3和方案4是相同的.各方案相对于指标层的社会资本因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从社会资本角度看，方案1、方案2、方案3和方案4是相同的.

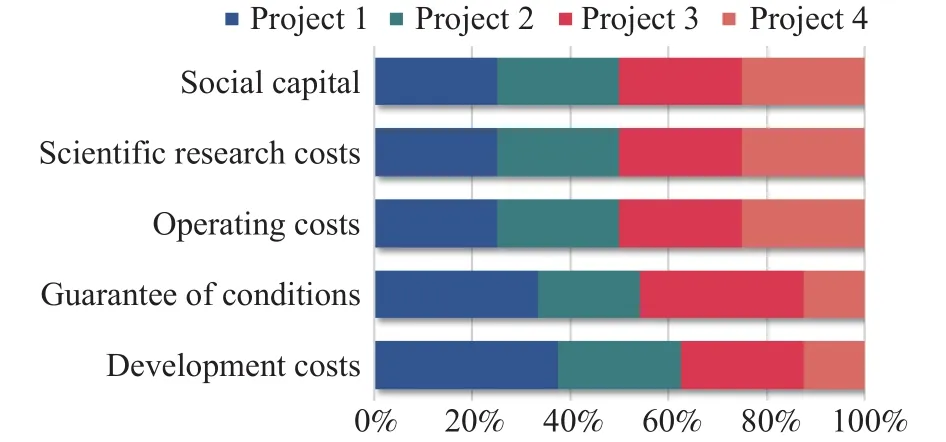
图7 各方案对经费对应指标层各元素的权重Fig.7 Weights of each element in the corresponding index layer for each program’s expenditure

2.4.4 周期指标分析

图8表示各方案对周期对应指标层各元素的权重.各方案相对于指标层的规划符合度因素来说，方案3所占权重最大，为0.375，其次是方案2和方案4，为0.25，最后是方案1，为0.125；从研制费角度看，方案3是最优的，其次是方案2和方案4，最后是方案1.各方案相对于指标层的计划可行性因素来说，方案3所占权重最大，为0.375，其次是方案 2和方案 4，为 0.25，最后是方案 1，为0.125；从计划可行性角度看，方案3是最优的，其次是方案2和方案4，最后是方案1.

图8 各方案对周期对应指标层各元素的权重Fig.8 Weights of each element in the index layer corresponding to the period of each scheme

2.4.5 效益指标分析

图9表示各方案对效益对应指标层各元素的权重.各方案相对于指标层的科学产出因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从科学产出角度看，方案1、方案2、方案3和方案4是相同的.各方案相对于指标层的技术推动因素来说，方案1、方案2和方案3所占权重相同，为0.208，低于方案4的0.375；从技术推动角度看，方案4是最优的，其次是方案1、方案2和方案3.各方案相对于指标层的社会影响因素来说，方案1、方案2和方案3所占权重相同，为0.208，低于方案4的0.375；从社会影响角度看，方案4是最优的，其次是方案1、方案2和方案3.各方案相对于指标层的政治外交因素来说，方案2、方案3和方案4所占权重相同，为0.208，低于方案1的0.375；从政治外交角度看，方案1是最优的，其次是方案2、方案3和方案4.各方案相对于指标层的人才培养因素来说，方案1、方案2、方案3和方案4所占权重相同，为0.25；从人才培养角度看，方案1、方案2、方案3和方案4是相同的.各方案相对于指标层的成果转化因素来说，方案4所占权重最大，为0.375，其次是方案2和方案3，为0.25，最后是方案1，为0.125；从成果转化角度看，方案4是最优的，其次是方案2和方案3，最后是方案1.

图9 各方案对效益对应指标层各元素的权重Fig.9 Weights of each scheme to each element of corresponding index layer

2.5 方案决策结果

图10表示探月总体方案的总排序权值.通过探月总体方案的总排序可得探月总体方案的总排序权值是：方案1是0.226，方案2是0.245，方案3是0.292，方案4是0.237，按照总效能进行排序的结果是：方案3＞方案2＞方案4＞方案1，从而可选出最优方案是由长征四号丙发射中继星，长征三号乙发射着陆器和巡视器组合体.

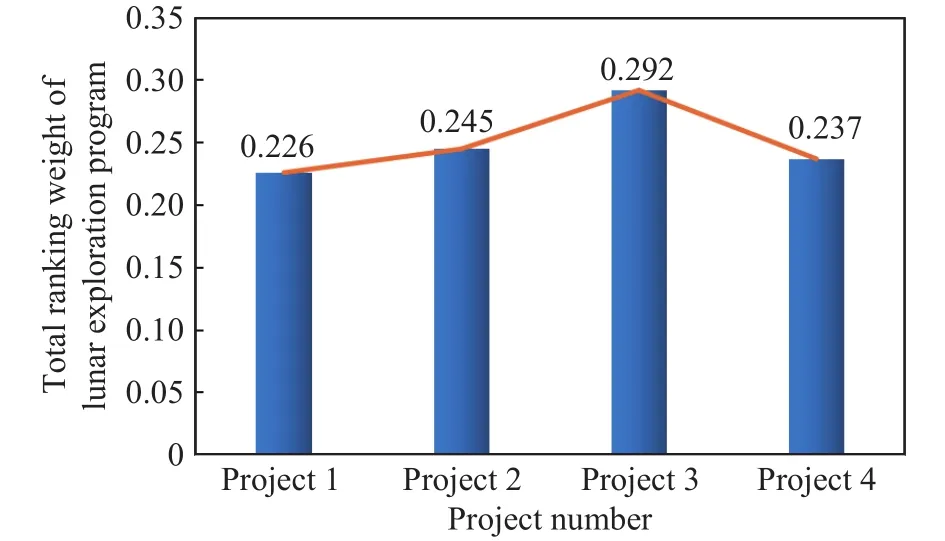
图10 探月总体方案的总排序权值Fig.10 Total ranking weight of lunar exploration program

3 结论

（1）本文基于模糊层次分析模型，考虑技术、科学、经费等多指标多层次结构，构建了中国探月工程总体方案的优选方法体系.模糊层次分析法通过模糊的方式,快速做出判断，可以避免应用传统层次分析法进行决策时，出现判断不一致情况，有利于站在国家层面遴选最优总体方案，使各相关方能尽快达成共识，同时也有益于国家科学决策.

（2）基于模糊层次分析模型的中国探月工程方案的主控因素分析表明：技术、科学和经费相对于周期和效益更为重要.先进性、可靠性是技术准则下的主控因素；科学价值是科学准则下的主控因素；研制费是经费准则下的主控因素；规划符合度、计划可行性是周期准则下的主控因素；科学产出、技术推动是效益准则下的主控因素.

（3）利用已实施的嫦娥四号任务方案，对模型的可行性、适用条件和范围进行验证.综合专家判断和理论分析，建立各层次指标下的判断矩阵，进而计算权重系数.计算结果表明嫦娥四号探月任务的最优方案是由长征四号丙发射中继星，长征三号乙发射着陆器和巡视器组合体，这也与实际情况相一致，验证模型的正确性.本研究可为我国后续各类深空探测方案制定提供快速及科学的理论支撑.