基于竹子结构的装载机动臂仿生轻量化设计

徐玉凯， 祝海林,2， 何宜玖， 周扬驰

(1.常州大学 机械与轨道交通学院， 江苏 常州 213164； 2.江苏省绿色过程装备重点实验室(常州大学)， 江苏 常州 213164)

装载机是工程建设中的施工机械，被广泛应用于许多领域，比如道路、桥梁、大坝等，对减少体力劳动，提高作业效率，保证施工质量起着重要作用[1-3]。然而，装载机在设计时常为保证寿命与安全性，普遍采用加厚设计的动臂，材料出现富余，装载机也较为笨重；动臂质量的增加将进一步提升装载机油耗，不仅造成工作成本的增加，而且导致能源的浪费，因此对装载机进行轻量化研究尤为重要[3-6]。赵磊等[7]对装载机动臂的厚度进行多目标优化设计，通过减轻动臂板材的厚度让动臂质量下降13.16%，从而实现装载机轻量化，但装载机厚度的减轻很大程度致使动臂承载能力下降。霍亚光等[2]利用拓扑优化的方法使装载机动臂的质量下降了19.25%，但其通过挖孔的处理方法降低动臂的质量，会一定程度上降低装载机的强度与刚度。竹子是自然界中典型的具有质量轻、刚度高、强度大、性能稳定的生物体，这与竹子的中空夹层的柱状体结构有着密切关系[8-10]，受竹子内部结构的启发，在研究典型的轮式装载机构型特点及其动臂静力学分析、有限元仿真的基础上，设计了仿生动臂结构，并在正载插入、正载掘起、偏载插入、偏载掘起4种工况下，分别对原动臂与仿生动臂进行有限元分析对比。

1 装载机工作装置组成原理

2 装载机动臂静力学计算与有限元分析

动臂是装载机重要工作部件，其作业条件恶劣，易发生损坏。为了保证装载机的工作安全，装载机动臂通常做加厚处理，以提高其强度，但动臂的强度往往富余很多，造成装载机工作装置质量增加，能耗上升。因此，深入分析动臂在极限载荷时的受力状况，以改善动臂的结构进而降低其质量，实现装载机轻量化，有较大实际意义。

装载机在正常工作时主要有4种工况[10]：① 正载插入工况，即铲斗仅受水平阻力的对称切入工况；② 正载掘起工况，即铲斗仅受竖直阻力的对称加载工况；③ 偏载插入工况，即铲斗仅受水平阻力的偏心切入工况；④ 偏载掘起工况，即铲斗仅受竖直阻力的偏心加载工况。文章就此4种工况分别对动臂进行静力学计算与有限元分析。

2.1 动臂静力学计算

为确保动臂在4种工况下满足强度要求，需计算出装载机工作装置极限水平插入阻力与竖直掘起阻力。图2为装载机铲斗的受力图，其中，G为铲斗和物料的重力，L1为载荷作用点到铰接点B的水平距离，L2为铲斗和物料的质心点到铰接点B的水平距离，L3为载荷作用点到铰接点B的垂直距离。

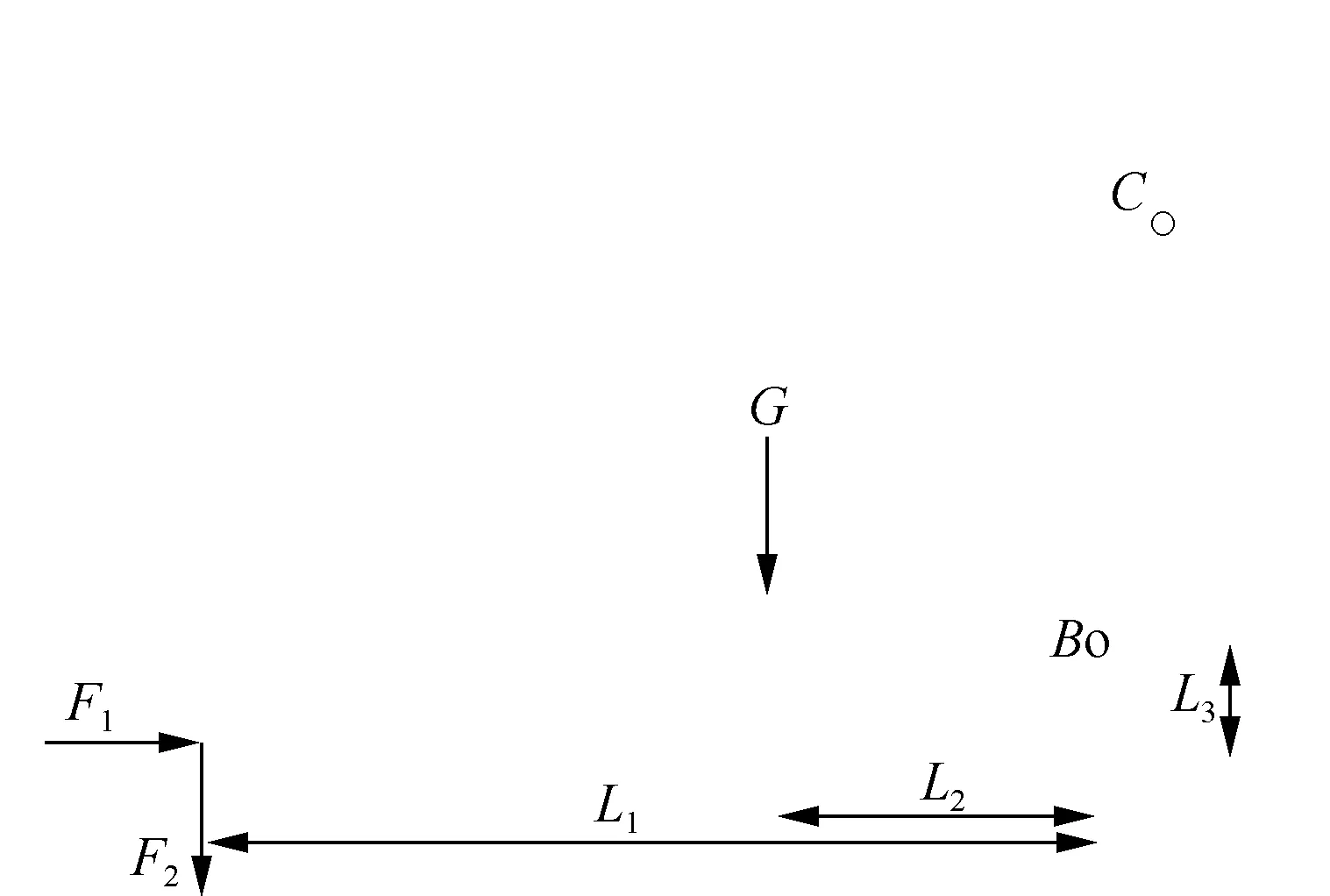
图2 装载机工作装置铲斗受力模型Fig.2 Force model of loader bucket

工作装置的水平插入阻力F1为

(1)

式中：k为物料综合影响因数；b为铲斗宽度；L0为铲斗插入物料的深度。

据ZL50型装载机铲斗二维图纸可知，b=300 cm，L0=77 cm，k=0.24。由式(1)计算可得装载机水平插入阻力F1=161 kN。

工作装置的竖直掘起阻力F2为

经过对取样的研究分析，可以判断鲕粒的形成过程为：有一粒灰岩碎屑，在海水中不断悬浮沉降，形成多层同心层，成为真鲕。其后由于粒度变大，悬浮较困难，碰撞、摩擦相应变少，有微生物开始附着生长，在周期性的潮汐作用下，不断滚动生长。但是某些环境因素的改变，导致微生物逐渐消亡。在鲕粒的最后生长阶段，形成的鲕层与胶结物无异。最后，由于泥质的加入形成一层光滑的泥质薄膜，终止了鲕粒的生长，最终形成巨型鲕粒。鲕粒形成的环境始终是动水环境。

(2)

铲斗二维图纸中，L1=120 cm，L2=68 cm，L3=41 cm，G=50 kN。由式(2)计算可得竖直掘起阻力F2=173 kN。

在铲斗初铲时，可认为动臂与机架、动臂与动臂油缸、动臂与摇臂的3个铰接处都不发生相对运动，动臂与铲斗铰接处上B点可作为动臂所受的外主动力。对铲斗进行受力分析，计算B点载荷，如图3所示。

图3 铲斗受力分析图Fig.3 Diagram of bucket force analysis diagram

铲斗受力平衡方程为

(3)

式中FC是图3中拉杆对C点产生的拉力。4种工况下，L1，L2，L3，L4，FSX，FSY的值为确定值，故而可计算出FC，FBX和FBY。由于装载机工作装置是对称结构，所以正载插入时FSX=F1，FSY=0，FBX,L=FBX,R=FBX/2，FBY,L=FBY,R=FBY/2；正载掘起时FSX=0，FSY=F2，FBX,L=FBX,R=FBX/2，FBY,L=FBY,R=FBY/2。偏载工况时，载荷集中于一点并位于铲斗最边沿，此为偏载受力情况，载荷为偏载力。根据力线平移定理，将偏载力平移到铲斗中间，同时在铲斗上增加一个附加力偶即可与铲斗偏载工况产生等效的受力。附加力偶使铲斗左右两端B点上分别添加大小相同、方向相反的两个力。因此，偏载插入时FBX,L=FBX/2+(F1×b)/(2×L5)，FBX,R=FBX/2-(F1×b)/(2×L5)，FBY,L=FBY,R=FBY/2；偏载掘起时FBX,L=FBX,R=FBX/2，FBY,L=FBY/2+(F2×b)/(2×L5)，FBY,R=FBY/2-(F2×b)/(2×L5)。其中，FBX，FBY与正载是相同，L5是动臂上左右B点之间的距离，尺寸参数为210 cm。将F1=161 kN，F2=173 kN带入上列方程计算，结果见表1。

表1 B点边界条件计算结果Table 1 Calculation results of boundary conditions at point B kN

2.2 动臂有限元分析

2.2.1 网格数无关性检验

在Solidworks中绘出动臂三维模型，再应用ANSYS对三维模型进行有限元仿真，动臂材料是16Mn, 动臂质量为1 331.3 kg，性能参数见表2。

表2 16Mn材料性能参数Table 2 Performance parameters of 16Mn material

动臂结构规则对称，采用映射网格划分，选择四面体结构，并对铰接孔处进行网格局部加密[11]。网格划分出的不同网格总数对应力值有较大影响，为证明网格的划分已具有足够精度描述应力结果，需检验网格的无相关性。分别设置网格单元精度为300，40，30，20，15，10 mm，对应划分网格总数为10 513，32 044，41 659，92 374，157 085，361 818。对动臂施加边界条件，A点设置为固定铰接约束，D点设置为平行于限制转斗油缸直线方向上的移动自由度，E点设置为限制动臂油缸直线方向上的移动自由度。

动臂工作工况对网格的无相关性检验几乎无影响，取正载插入工况进行分析，以减少计算机工作时间，提高计算效率。上述网格划分对应仿真计算出的最大等效应力分别为44.267，47.650，47.997，48.232，48.230，48.284 MPa。图4为网格数对应应力变化图，图5为10 mm单元精度时，动臂应力云图中最大等效应力红色区域网格显示图。

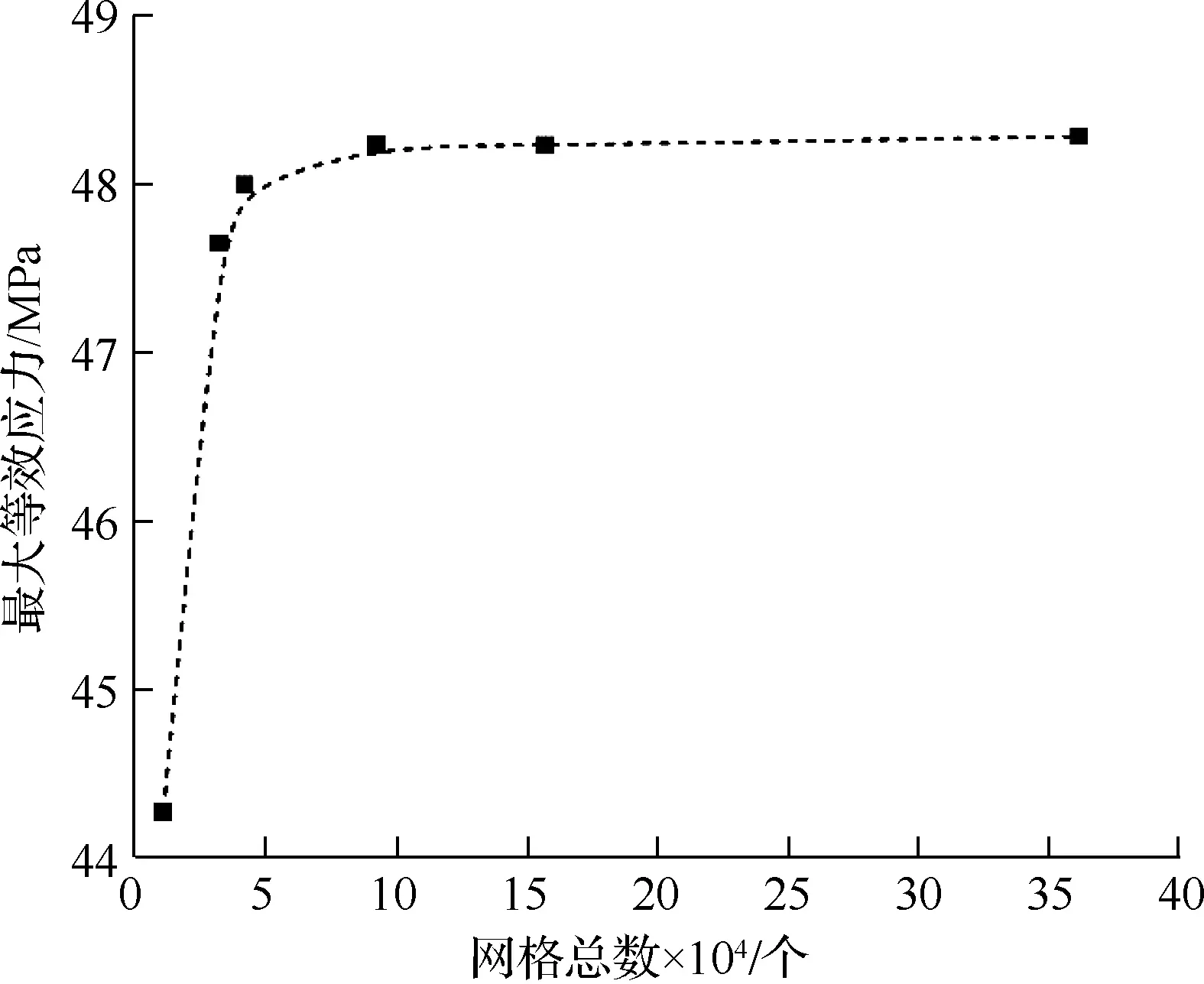
图4 网格数对应应力的变化Fig.4 The number of grids corresponds to the change of stress

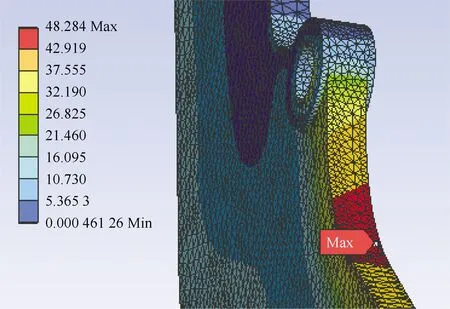
图5 最大等效应力网格显示图Fig.5 Grid diagram of maximum equivalent stress

由图4可看出随着网格总数增加，最大等效应力趋于稳定。在网格为157 085和361 818时，最大等效应力值的前后差距已在5%之内，可见网格划分的精度已经足够，此为该网格无相关性依据之一。为提高仿真数据精确性，选取网格总数为361 818的网格。

图5中显示的是10 mm单元精度，网格总数为361 818的网格划分下的最大等效应力值红色区域，该红色区域完整覆盖超过2个单元以上，此为依据之二。综上2点依据，即可证明该网格无相关性。

选用单元精度为10 mm，网格总数为361 818的网格，并将表1中的边界条件施加到B点。4种工况下的仿真结果如图6所示。

(a) 正载插入时动臂应力云图

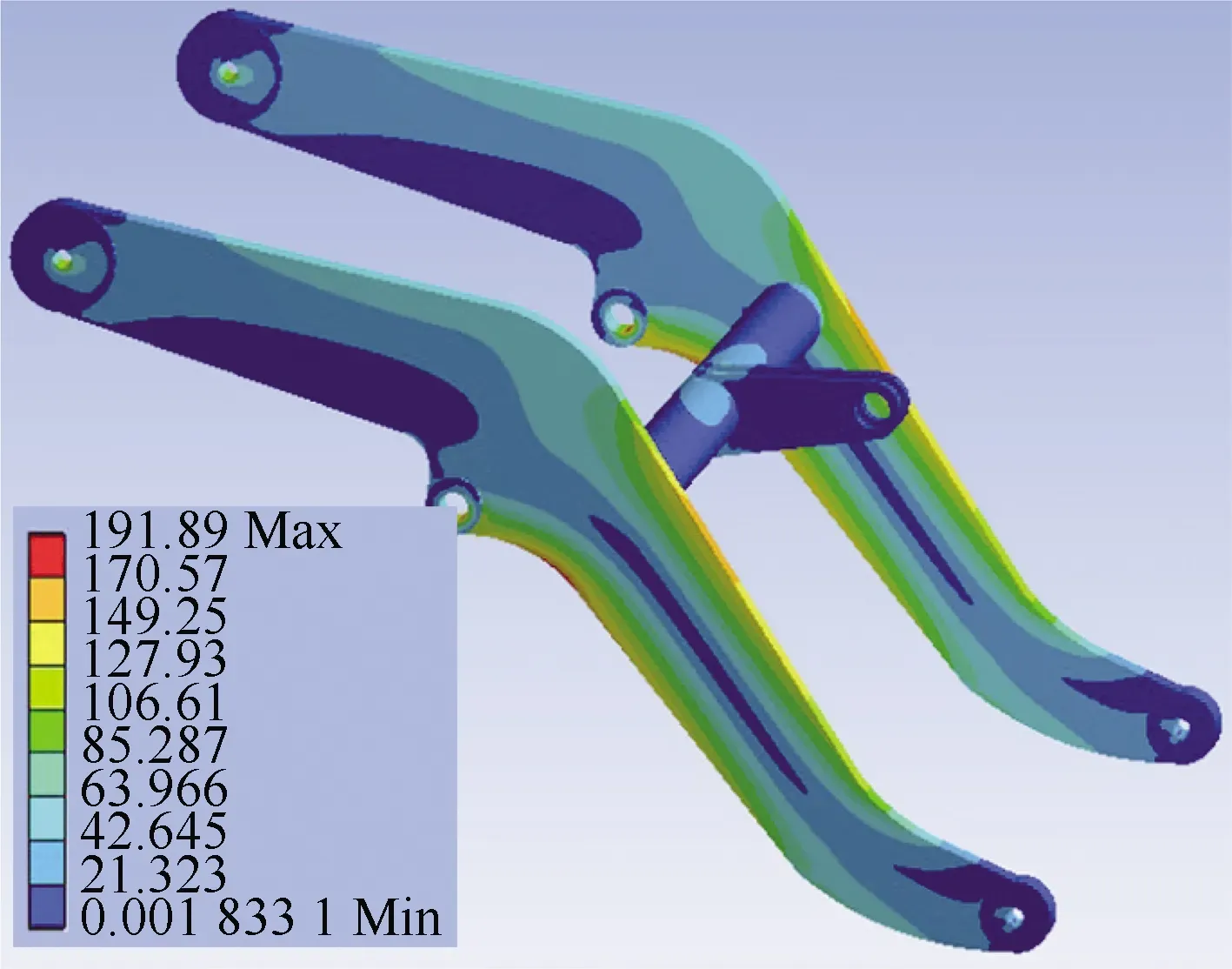
(b) 正载掘起时动臂应力云图

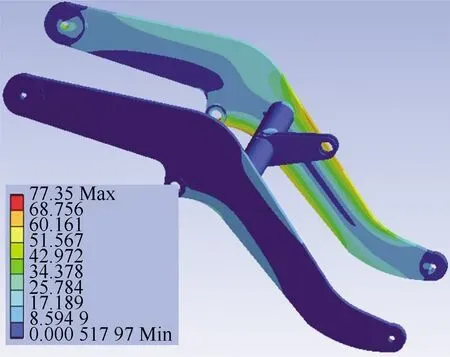
(c) 偏载插入时动臂应力云图

(d) 偏载掘起时动臂应力云图图6 4种工况下动臂静力分析云图Fig.6 Cloud images of static analysis of swing arm under four working conditions

图6显示动臂在4种工况下的最大等效应力分别为48.284，191.89，77.35，219.29 MPa，与动臂材料的屈服极限相比，4种工况的最大等效应力均在安全范围内，满足力学要求。同时可以看出该动臂在4种工况下的应力集中主要位于动臂油缸与动臂的铰接处；动臂左右动臂板的上下两段中心区域应力较小、材料盈余较多、强度富裕，这为优化动臂提供可能，也为动臂的轻量化设计提供了仿生空间。

3 动臂仿生轻量化设计及其有限元分析

3.1 仿生动臂结构设计

在自然界中，竹子是典型的具有重量轻、刚度高、强度大、性能稳定的植物，这与竹子自身的特殊空间结构有着密切关系。竹子在外界环境之中，主要承受风载，产生弯矩，发生弯曲变形，这与动臂两侧板的载荷状况类似。因此，文章选用竹子作为仿生研究对象，取其自下而上20节竹筒，对每节竹筒的外径与壁厚进行测量，将壁厚与外径比值定义为竹子的厚径比，测量结果如图7(a)所示。由图7(a)可见，随着竹子高度的增加，厚径比并没有明显变化，且稳定于一个数值 0.15。由此可以推测，竹子优异的力学性能应该与其厚径比有关，即在厚径比为 0.15 时，竹子整体耗费的材料最少，以最轻的质量，产生最佳的力学性能。

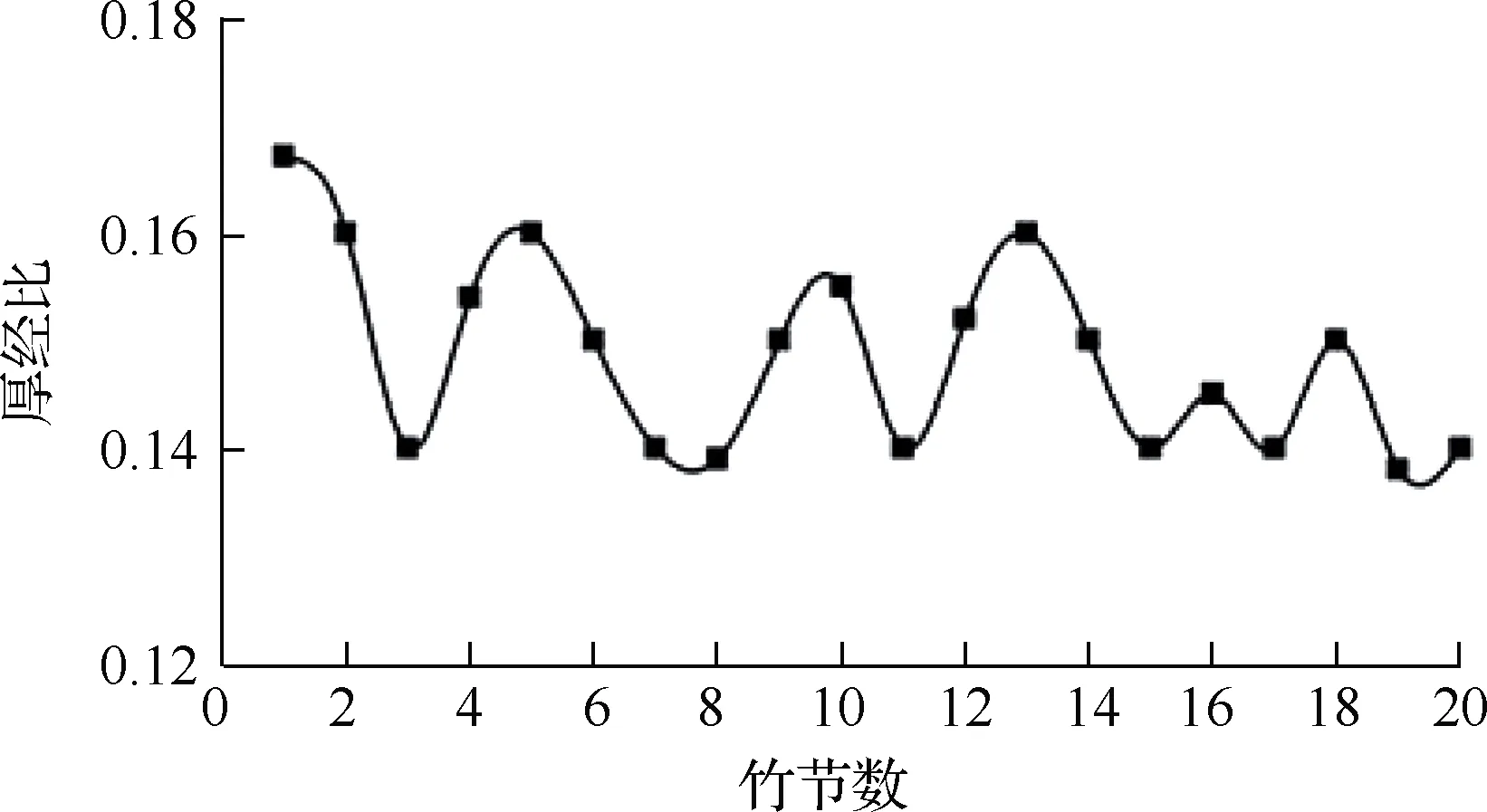
(a) 竹子厚径比随竹节数的变化关系

(b) 竹子受力前后截面变化图7 仿生竹子结构相关特点Fig.7 Related characteristics of bionic bamboo structure

竹子截面一般近似为圆形，在受到外界载荷F后，竹子截面变形为近似椭圆或近似腰形。在外界现实环境中，竹子长时间处于受力摇动状态，不会始终保持静止，截面的变形属于常态。受此启发对不同截面竹子的性能进行研究。为校验不同截面仿生竹子结构的性能，加入具有优异性能的蜂巢正六边形结构进行对比分析，如图7(b)所示。

设计相同长度、外径的4种厚径比为0.15的中空柱状体仿生微结构，材料为16Mn，其截面分别为圆形、椭圆形、腰形及正六边形。对4种仿生微结构分别进行有限元分析，上下添加2块相同的盖板，在上端面负载5 000 N、下端面固定约束，4种截面的微结构仿真结果如图8所示。

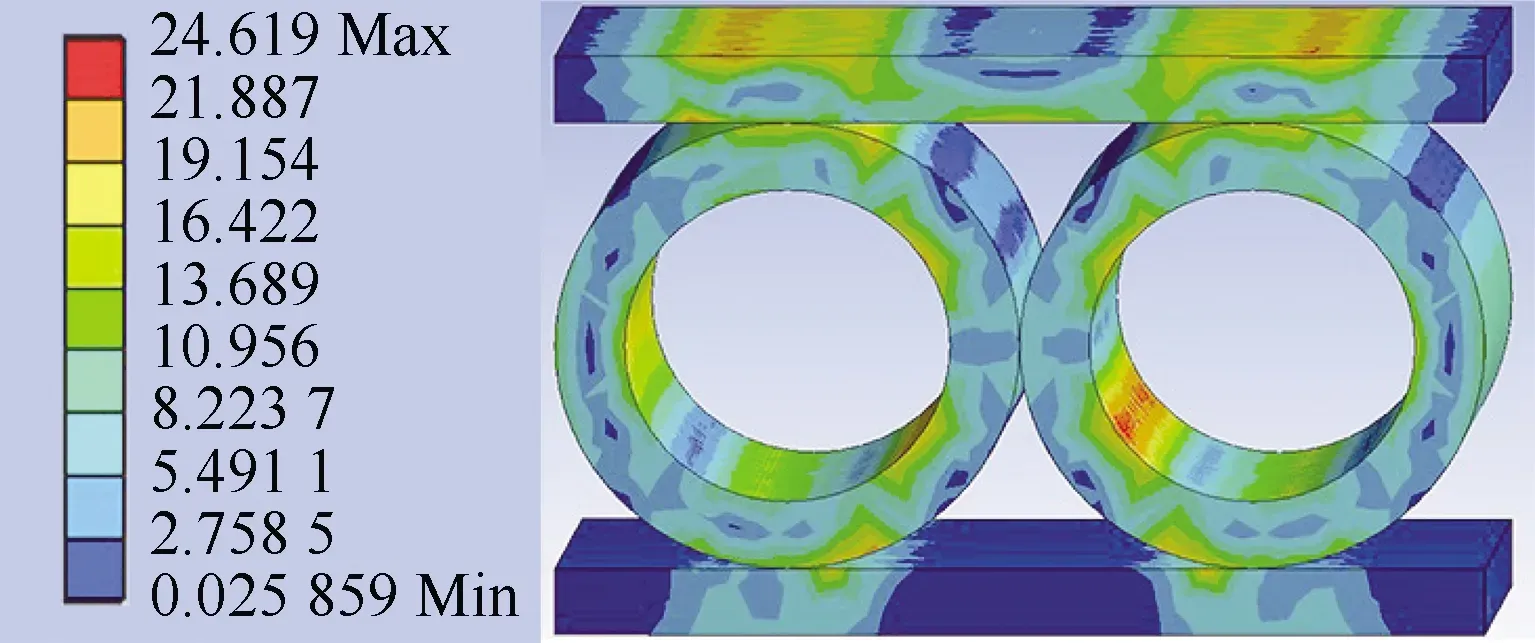
(a) 圆形截面微结构应力云图

(b) 椭圆形截面微结构应力云图

(c) 腰形截面微结构应力云图

(d) 正六边形截面微结构应力云图图8 4种截面的仿生结构受力分析Fig.8 Stress analysis of four kinds of bionic structures

4种截面的中空柱状体数据对比见表3，其中腰形截面的中空柱状体结构产生的最大等效应力值最小，形成的总位移也是最小，力学性能最佳，由此可以选择腰形仿生微结构进行动臂设计。

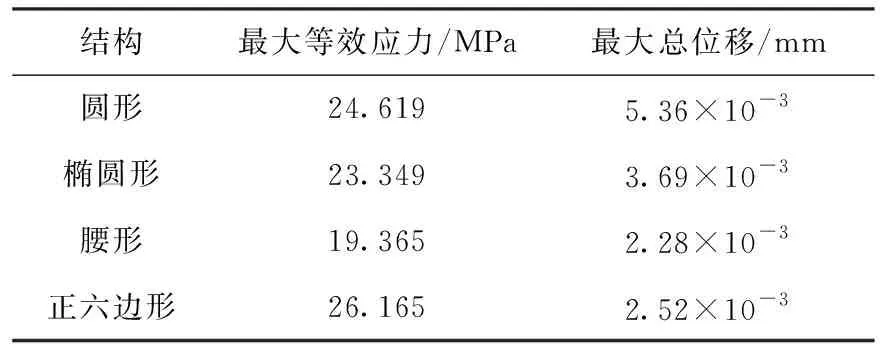
表3 仿生微结构数据对比Table 3 Comparison of microstructure simulation data

竹节是竹子自身十分重要的一个特征，国内学者对带竹节与不带竹节的竹子进行试验[12]，结果显示带竹节比不带竹节的竹子抗弯强度、抗剪强度都高，其中抗弯强度尤为明显。这些竹节可看作为竹子上排布的加强筋，防止竹子弯曲变形，增加了竹子整体的强度与稳定性。实际中竹子各竹节之间的间距是随外径而变化的，文章中的中空柱状体为等径中空腰形，其外径为固定值，故而作为仿生竹节的加强筋在使用时可等间距排布。

前面有限元分析中显示原动臂两侧板的上下段中心区域在4种工况下应力较小，材料盈余较多，可以选取该部分进行结构仿生设计，结果如图9所示。图9(a)为仿生动臂三维结构图，图9(b)为图9(a)的剖面图。以腰形截面、厚径比为0.15的双排中空柱状体作为基础，横向排布于仿生空间。在双排中空柱状体两侧等距的加入长肋板作为加强筋，增加仿生结构的承载力与稳定性，从而在保证仿生动臂力学性能的基础上进行有效轻量化处理。

(a) 仿生动臂三维结构图

(b) 仿生动臂仿生部分剖面图图9 仿生动臂图Fig.9 Imitation of vivid arm diagram

3.2 仿生动臂结构有限元分析

对仿生动臂进行有限元分析，边界条件与原动臂相同，划分网格总数为1 387 807，节点总数为744 353,质量为1 104.6 kg，仿真结果如图10所示。

图10中4种工况下的最大等效应力分别为54.385，216.12，91.814，249.74 MPa，与仿生动臂材料的屈服极限345 MPa相比，4种工况的受力情况都在安全范围内，与原动臂相比质量减轻了17.03%，实现了装载机动臂的轻量化。

(a) 正载插入时仿生动臂应力云图

(b) 正载掘起时仿生动臂应力云图

(c) 偏载插入时仿生动臂应力云图

(d) 偏载掘起时仿生动臂应力云图图10 4种工况下仿生动臂静力分析云图Fig.10 Cloud images of static analysis of bionic swing arm under four working conditions

4 结 论

1) 在分析装载机工作原理、动臂边界条件及其有限元仿真的基础上，得出了装载机动臂的强度特征，满足力学要求，并且确定了应力集中、材料富裕区域，这为装载机动臂的优化提供了参考。

2) 通过对竹子结构的深入分析研究，可得出厚径比为0.15、截面为腰形、等距排列加强筋的中空柱状体仿生结构力学性能优异。该结构具有质量轻、强度大、变形量小的优点，可作为仿生竹子轻量化结构的首选。

3) 仿生处理后的动臂，在满足强度要求的前提下，动臂质量减轻了17.03%，表明仿生竹子结构进行装载机动臂的轻量化设计与节能降耗是可行的、有效的。