水驱油田动态相对渗透率计算方法适用性研究

刘新光，李南，张金庆，张利军，郑伟

1.中国海洋石油国际有限公司海外技术支持中心，北京102200 2.中海油研究总院有限公司勘探开发研究院，北京102200

油水相对渗透率曲线(以下简称相渗曲线)是油田开发最为关键的基础参数，是水驱油田含水上升规律、产量递减规律和采收率的决定因素[1,2]。实际油田开发过程中，由于岩心取样数量和试验费用的制约，往往仅对部分层位、井区开展相渗曲线试验。随开发时间的增长，相渗曲线会发生变化[3,4]，可能与早期试验测试的相对渗透率相差较大。动态相渗曲线是通过生产井的实际油水产量反求得到的油水相渗曲线，既反映了实际岩石和流体特性，也包括了真实油藏的非均质性[5]。在方法合理的情况下，动态相渗的代表性较强，对油田开发后续预测更具指导作用。由于反函数的求解具备一定的多解性，一些文献中使用多次迭代[6,7]或者遗传算法[8]来寻找最优解的方式确定相渗的关键参数，但需要编程计算，方法求解难度较大，多次迭代也增加了不可控性，很多算例难以得到合理的结果。文献[9.10]采用相对渗透率的指数表达式，直接利用含水率与水油比的关系来计算相渗曲线，简化了曲线求解的过程。文献[11]采用相渗曲线指数表达式推导了张型近似理论水驱曲线，通过生产数据拟合水驱曲线求解待定参数来确定相渗关键参数，得到动态相渗。

在实际应用中发现，不同方法计算结果存在较大的差异，需要科学对比确定合理的计算方法，明确方法的适用油藏类型，以便对后续应用进行指导。通过数值模拟计算的油水产量数据，使用不同方法计算动态相渗曲线，对比动态相渗与数值模拟输入相渗及动态相渗计算的无量纲采油采液指数和模型中输出的产量、压差数据计算的无量纲采油采液指数[12]来综合判断动态相渗计算方法的合理性，并验证方法对油藏类型的适用性。

1 数值模型的建立

采用Eclipse软件建立数值模拟模型。

注水油藏直井开发模型(见图1(a))：网格数为21×21×20，网格步长为20m×20m×1m，地层倾角为0°，无天然水体，孔隙度30%，渗透率1500mD，原油黏度μo=50mPa·s，地层水黏度μw=0.5mPa·s，模型输入相渗为渤海辽东湾地区某油田实验室测定的相渗曲线(如图2所示)。该类油藏常采用直井规则井网开发，取五点注水井网的1/4模型(1注1采)，注采井间距594m，模型厚度20m，生产控制条件为定油限液限流压生产，生产井日产油量目标300m3，最大日产液量1000m3，最低井底流压4MPa；注水井最高注入量1000m3/d，注采平衡，最高井底流压14MPa，生产时间20年。

边水油藏水平井开发模型(见图1(b))：网格数15×30×10，网格步长20m×20m×1m，地层倾角3°，水体倍数20倍。该类油藏适合采用水平井天然能量开发，以促进水线均匀推进，设计水平井长度280m，水平井距内含油边界400m，其他条件同注水油藏直井开发模型。

底水油藏水平井开发模型(见图1(c))：网格数21×21×20，网格步长20m×20m×1m，地层倾角0°，水体倍数20倍，该类油藏适合采用水平井天然能量开发，尽量缓解底水锥进速度。设计水平井长度280m，避射高度20m，其他条件同注水油藏直井开发模型。

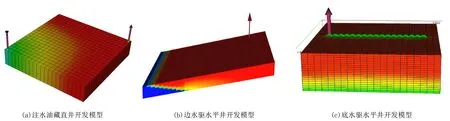
图1 不同油藏类型开发模型示意图

2 动态相渗求解方法的验证

采用注水油藏直井开发模型计算结果，对应用较广的水油比法和张型近似理论水驱曲线法进行验证。

2.1 水油比法合理性验证

相渗的指数式表达式：

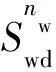
(1)

Kro=Kro(Swi)(1-Swd)no

(2)

根据平面径向流公式：

(3)

(4)

式中：Kro、Krw分别为油相相对渗透率、水相相对渗透率，1；Krw(Sor)为残余油饱和度下的水相相对渗透率，1；Kro(Swi)为束缚水饱和度下的油相相对渗透率，1；Swd为归一化的含水饱和度，1；no、nw分别为相渗的指数式表达式中的油相指数、水相指数，1；Qo、Qw分别为产油量、产水量，m3/d；K为有效渗透率，mD；h为油层厚度，m；Δp为生产压差，MPa；μo、μw分别为地层原油黏度、地层水黏度，mPa·s；Bo、Bw分别为油相体积系数、水相体积系数，m3/m3；re、rw分别为泄油半径、井筒半径，m。

假设油水相生产压差相等、供液半径相同，并将式(1)、式(2)代入式(3)、式(4)，可得到水油产量比为：

(5)

根据定义，Swd可表示为可动油储量采出程度Rf，即:

(6)

对式(5)两边取对数并将式(6)代入可得到二元一次方程形式：

(7)

其中:

(8)

式中：Np为某一时刻累计产油量，m3；NR为含水率到达100%时的累计采油量，m3；M为水油流度比与油水体积系数比的乘积，1。

使用甲型水驱曲线拟合数值模拟结果中产油、产液量数据，得到NR=30.4×104m3，之后拟合式(7)，多元回归得到M=71.3，nw=2.43，no=1.34。根据式(8)得到Krw(Sor)=0.713，之后根据式(1)绘制出相渗曲线，如图2所示。对比可见，水油比法计算的动态相渗曲线明显高于数模相渗，两者存在着较大差异。

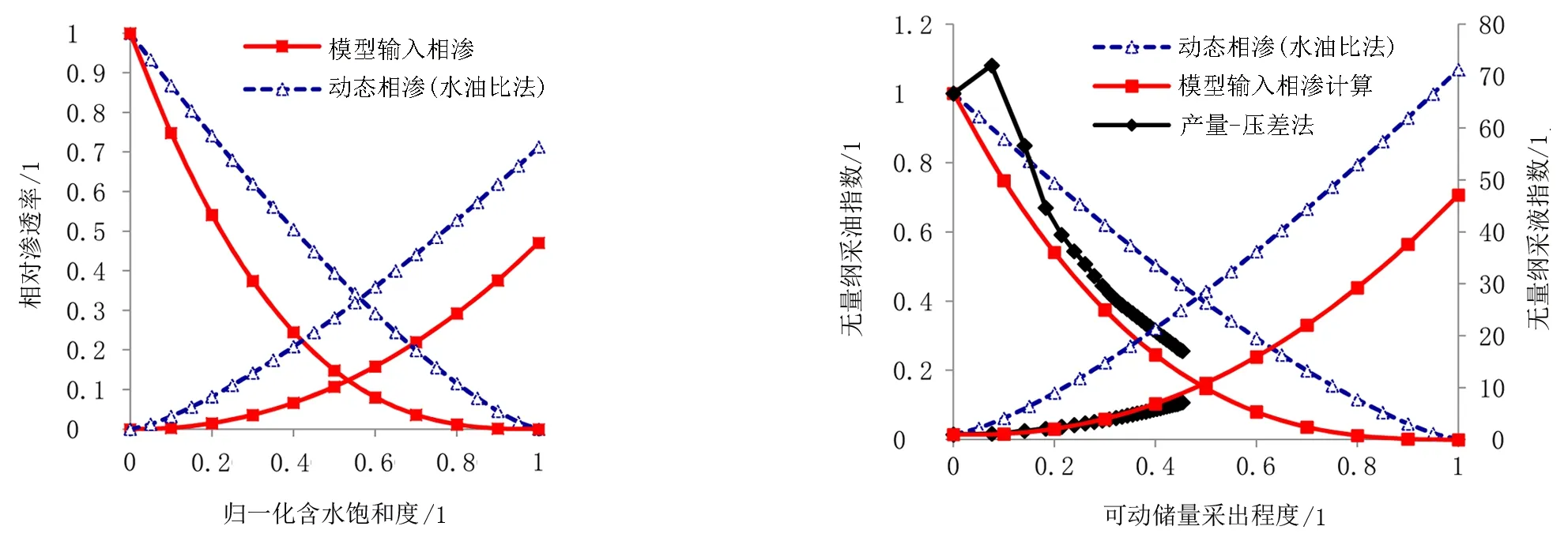
图2 水油比法动态相渗与模型输入相渗比较 图3 水油比法动态相渗与模型输入相渗和产量-压差计算无量纲采油采液指数比较

无量纲采油、采液指数为某一时刻下的采油、采液指数与初始状况下的采油、采液指数的比值，其定义为式(9)。图3中黑色实线为模型中产油、产液和生产压差数据计算得到的无量纲采油、采液指数曲线。

(9)

根据文献[11]，无量纲采油、采液指数可使用相渗参数表示为式(10)，可分别绘制出水油比法动态相渗和模型输入相渗对应的无量纲采油采液指数曲线，如图3中的蓝色虚线和红色实线。

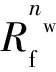
(10)

式中：Jdo、Jdl分别为无量纲采油指数、无量纲采液指数，1；Jo、Jl分别为某一时刻下的采油指数、采液指数，m3/(MPa·d)；Joi、Jli分别为无水采油期的采油指数、采液指数，m3/(MPa·d)；Rf为可采储量采出程度，1。

模型中每个网格均按照输入相渗进行计算，若动态相渗计算方法正确，回归得到的动态相渗应与模型的输入相渗接近；使用动态相渗计算的无量纲采油采液指数应该与模型给出的压差-流量计算的无量纲采油采液指数接近，这种情况下采用动态相渗才具有其对实际生产的预测和指导意义。通过对比可见，由水油比法绘制的无量纲采油采液指数高于数模输入相渗和根据产量-压差计算得到的无量纲采油采液指数。这说明水油比法计算的动态相渗误差过大，不能代表实际相渗，由此计算的无量纲采油采液指数也不能用于现场预测。水油比法假设油相、水相的压差和泄油半径相同，其过程类似于稳态法油水相渗试验过程[13，14]，即在油藏或岩心的一端注入一定比例的油和水，在另一端产出相同比例的油和水。而实际油田的开发类似于非稳态法相渗试验过程，即在油藏或岩心的一端注入水，在另一端产出油和水，生产过程中油相和水相的压差、饱和度都在不断变化，不能近似为相等，式(5)不能成立。

2.2 张型近似理论水驱曲线法合理性验证

文献[11]根据相渗的指数式表达式推导出了近似理论水驱曲线，建立了水驱曲线的回归参数与相渗关键参数之间的关系式，具体过程如下。

根据相渗的指数表达式及分流量方程，在忽略重力和毛细管压力时，可得到:

(11)

由于:

(12)

则:

(13)

式(13)无法积分，但在被积函数的分子上加上一项高阶小项后可近似得到：

(14)

式(14)可积分得到原函数，即:

(15)

整理可得到张型近似理论水驱曲线：

(16)

其中，p、q、a的表达式如下：

(17)

式中：Wp为累计产水量,m3；p、q、a为张型近似理论水驱曲线法待定系数，1。

因此，通过生产参数回归张型近似理论水驱曲线，得到待定系数p、q、a后，可以计算相渗的关键参数nw、no、M及Krw(Sor)，从而得到动态相渗。由于该水驱曲线存在p、q、a、NR四个未知数，很难同时求解，具体操作过程中，建议首先假设p=2，即张型广适水驱曲线拟合得到q，再将p在2的基础上微调以使反算的Wp、fw拟合程度更高(图4(a))，再获得p、a(图4(b)中斜率的负数)、NR(图4(b)中的截距)3个参数。使用注水油藏模型输出结果拟合式(14)，如图4所示，求得的a=2.5342，q=0.75，NR=29.824×104m3，M=26.92，nw=1.65，no=2.34。

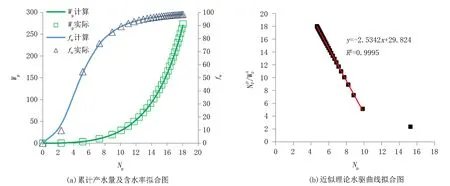
图4 张型近似理论水驱曲线拟合曲线

根据相渗参数，绘制动态相渗与模型输入相渗对比图(见图5)，可见张型近似理论水驱曲线法计算的动态相渗与模型输入相渗之间有一定的差异，但较水油比法差异明显减小。绘制不同方法的无量纲采油采液指数曲线图(见图6)，可见由张型近似理论水驱曲线法计算的无量纲采油采液指数与根据产量-压差计算得到的结果几乎完全重合，其精度高于根据模型输入相渗计算结果。可见，根据张型近似理论水驱曲线法计算的动态相渗能够综合考虑油田生产过程中相渗曲线、压力变化、平衡控制等一系列因素，虽然与模型输入相渗略有差异，但更能够代表油田总体情况，据此做出的预测也更加精确。

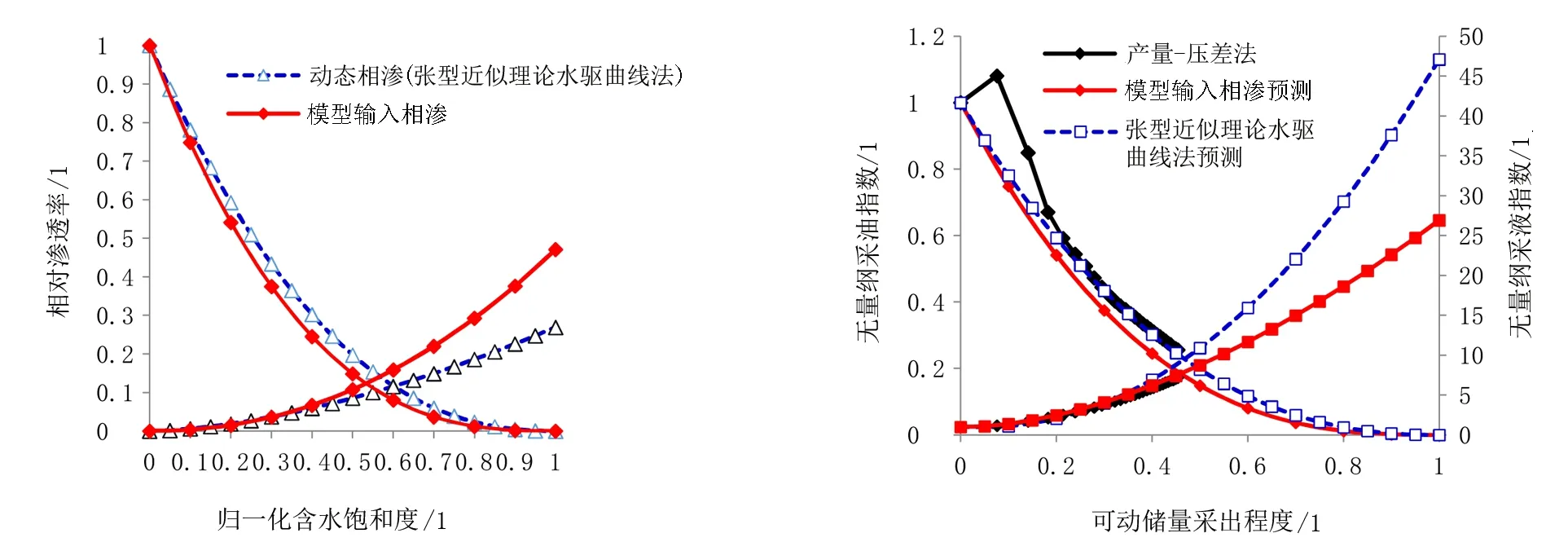
图5 张型近似理论水驱曲线法动态相渗产量-压差法计算无量纲采油采液指数比较图 图6 张型近似理论水驱曲线法、模型输入相渗和与模型输入相渗比较图

3 不同油藏类型验证

采用张型近似理论水驱曲线法，进行边水驱和底水驱油藏动态相渗的计算，并绘制无量纲采油采液指数对比曲线，结果如图7所示。对比可见，天然水驱边水油藏的动态相渗与模型输入相渗基本相同，根据相渗参数计算的无量纲采油采液指数曲线几乎完全重合，但两者与数模模型中根据产量-压差计算的采油采液指数略有差异；底水驱油藏的动态相渗与输入相渗差异较大，根据相渗参数计算的无量纲采油采液指数与模型中根据流量-压差计算的无量纲采油采液指数的差异也较大。由此可见，张型近似理论水驱曲线法计算的动态相渗对于倾角较小的注水开发油藏和天然边水驱动油藏的适应性较好，能够进行后续产量、提液时机等因素的预测[15]，但对于底水驱动油藏，由于公式(9)推导过程忽略了重力的影响，其误差较大。

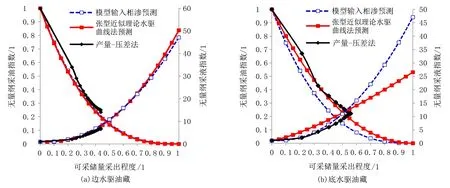
图7 天然水驱油藏水平井开发无量纲采油采液指数比较图

4 应用实例

SZ油田为典型海上注水开发油藏，以该油田处于油藏内部且开发历史较长、生产较为连续的D02井为例，其生产曲线如图8所示。采用张型近似理论水驱曲线法计算得到no=2.3，nw=1.7，M=31.5。该油田同一层位17条相渗曲线归一化后得到的no=2.19，nw=1.81，M=32.3。2种方法得到的相渗曲线对比图如图9所示(动态相渗无法计算束缚水饱和度与残余油饱和度，借用试验相渗Swi=0.31,Sor=0.25)。可见张型近似理论水驱曲线法计算的动态相渗与试验相渗曲线一致性高。因此，对于无试验相渗的已开发油田、区块或特殊的层位，可使用动态相渗作为参考。

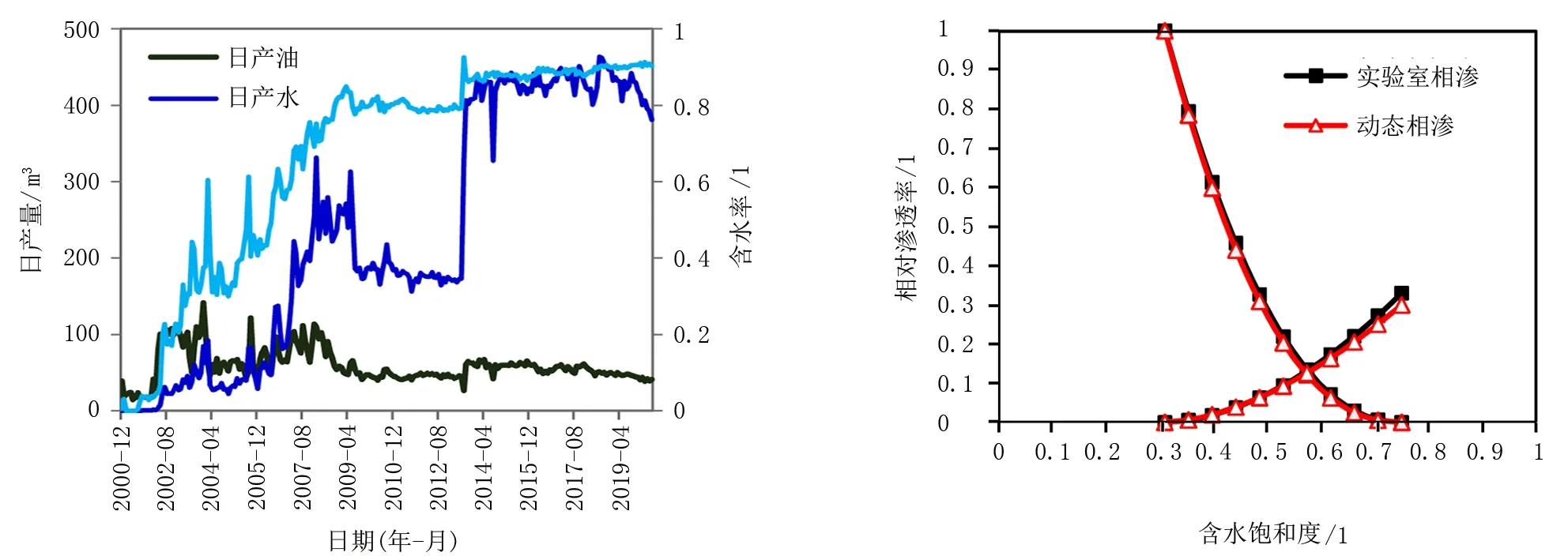
图8 SZ-D02井生产动态曲线 图9 实验室相渗与动态相渗对比图

5 结论

1)通过数值模拟机理模型中输入相渗和产量-压差法计算无量纲采油采液指数的对比表明，张型近似理论水驱曲线法的计算精度远高于水油比法；水油比法的物理意义基于稳态法相渗试验测定方法，其基本假设不适用于水驱油田开发过程。

2)地层倾角较小的注水开发油田和边水驱动油田中，张型近似理论水驱曲线法计算动态相渗预测精度较高，底水驱动油田的预测精度较低。

3)典型案例计算表明，张型近似理论水驱曲线法预测的动态相渗形态与实验室岩心相渗归一化结果较为接近，可以作为无实验相渗的油田、区块或层位的参考。