基于本地化差分隐私的空间数据近似k-近邻查询
张啸剑 徐雅鑫 孟小峰
1(河南财经政法大学计算机与信息工程学院 郑州 450002) 2(中国人民大学信息学院 北京 100872)
人工智能与大数据技术的迅猛发展,使得个人空间数据(例如移动用户位置、GPS位置、家庭住址等)的收集与分析变得尤为容易.服务方基于收集到的空间数据能够提高企业服务质量,以及开发出更具个性化的应用软件.近似k-近邻(knearest neighbor,kNN)查询是空间数据库与空间数据挖掘中的典型应用之一.例如,图1表示100万条纽约出租车位置数据(NYC)的散列图,给出kNN查询q1,要求返回与q1之间的距离满足r约束的6(k=6)个空间近邻位置点.然而,在响应q1查询的过程中,不可信的服务方有可能泄露6位乘车者或者查询者的个人空间位置数据,进而威胁个人的自身安全.主要原因是服务方收集了个人的原始空间数据,使得个人无法掌控自己的空间隐私数据.本地化差分隐私保护技术[1]的出现使得用户扰动自身数据之后再响应收集者的需求.目前基于本地化差分隐私着眼于频率估计、均值估计等研究,而涉及空间近似kNN查询的工作却很少.

Fig. 1 Spatial kNN queries on NYC图1 基于纽约出租车数据的空间kNN查询
在响应图1中的q1查询时,每个用户位置所对应的经纬度为个人的隐私信息.在利用本地化差分隐私对所有用户位置数据进行保护的过程中,通常需要对其进行本地编码与扰动.0/1编码是用户数据常用的编码技术.Basic-Rappor[2]算法利用0/1编码方案把用户数据编码成值域大小的二进制串.然而,该算法的误差与通信代价直接受值域大小的影响.Rappor[2]算法结合0/1编码与布隆过滤技术将长度为整个值域的二进制串Hash到较小的空间,减小了通信代价.不同于Rappor算法,UE[3]算法结合0/1编码与按位扰动技术实现了二进制串的保护,同时OUE[3]算法的误差摆脱了值域大小的影响.然而,这4种算法在保护用户位置时存在3点不足:1)无法满足保距性,即原始空间中近邻的数据点经过本地扰动后不再是近邻关系;2)会破坏用户位置经纬度的关联性;3)缺乏合理的数据结构来索引扰动后的空间数据点.
BV[4]算法利用连续区间分割与阈值过滤技术把数值数据嵌入匿名的汉明空间,再结合匿名空间求解数值数据之间的相似性.BV算法实现了匿名空间计算的保距性.然而,该算法存在隐私泄露风险[5],并且不适合大值域数值数据.DPRL[5]算法结合BV编码与Rappor扰动实现了满足本地化差分隐私的相似性度量.尽管DPRL实现了相似性计算过程的保距性,然而该算法存在缺乏对汉明空间压缩以及经纬度关联性易被破坏方面的不足.结合DPRL算法的不足,LSHPM[6]算法结合局部敏感Hash(locality-sensitive hashing, LSH)[7]与按位扰动技术实现了数据相似性度量.该算法利用Hash技术压缩了整个汉明空间,并利用单Hash表索引扰动之后的数据,实现了近似kNN查询.然而,该算法却存在没有充分利用LSH数据结构索引特性,即如何利用多Hash表与多Hash函数来提高kNN搜索碰撞概率方面的不足.总而言之,目前还没有一个行之有效且满足本地化差分隐私的空间kNN查询方法能够同时克服文献[4-6]所述算法带来的挑战.为此,本文基于本地化差分隐私技术提出了2种空间kNN查询算法以解决文献[2-6]所述算法存在的问题.
本文主要贡献有3个方面:
1) 为了有效解决现有0/1编码机制不能保持用户经纬度之间的关联性以及0/1串过长带来的通信代价过大问题,本文首先结合欧氏空间与汉明空间之间的映射关系提出了Embed嵌入算法,该算法能够将用户的位置嵌入到汉明空间.结合嵌入操作所得到的0/1串,提出了基于LSH数据结构的0/1串压缩算法,该压缩算法充分利用多Hash表索引与多Hash函数映射2方面优点来实现空间位置的保距性.
2) 为了提高kNN查询结果的可用性,本文利用隐私预算分割与用户分组策略设计了2种近邻kNN查询算法PELSH与PULSH.基于这2类算法,设计了4类本地扰动算法PELSHB,PELSHG,PULSHB与PULSHG.收集者通过这4类扰动算法重构多Hash表结构.
3) 理论分析了本文提出的算法满足ε-本地化差分隐私以及响应kNN查询的误差边界.通过真实数据实验分析,本文所设计的近似空间kNN查询算法具有较高的可用性和查询准确性.
1 相关工作
本地化差分隐私保护模型通常在假设收集者不可信的情况下收集用户的敏感数据.每个用户本地编码与本地扰动自身数据,然后报告给收集者.本地化差分隐私目前的研究主要集中于频率估计[3,8-9]与均值估计[10-11].GRR[8]机制在WRR[9]机制的基础上以直接编码方式转换用户数据,然后将用户数据扰动成原始值域中的某个值.该机制的估计误差容易受到原始数据值域的影响,值域过大导致误差过高.Duchi等人[10]所提的算法通过数值离散化与本地扰动操作,估计某连续区间中的均值.然而,该算法通常造成扰动结果过大地偏离真实值.PM[11]算法能够将某连续区间中的真实值扰动到一个连续区间,并给出相应的扰动边界.在隐私预算比较大时,PM算法优于Duchi等人的算法.
本地化差分隐私环境下,收集者通常结合层次结构设计隐私预算分割与用户分组策略来提高估计精度.PrivTrie[12]算法是用户分组与隐私预算分割策略的典型代表,该算法利用这2种策略重构前缀树,并结合前缀树挖掘频繁项.HH[13]算法与HI[14]算法分别利用B-ary树对用户数据进行索引,并利用树层次结构实现用户分组.PLDP[15]算法利用分类树结构实现了用户分组,结合分类树与SHist[16]算法收集所有空间用户的位置数据,并实现用户个性化隐私保护需求.然而,该算法的扰动方法没有顾及空间位置数据近邻性.GT-R[17]算法利用网格编码与四分树索引实现了用户分组,利用OUE[3]算法进行扰动,并能够较高精度地响应空间范围查询.然而,该算法在编码与扰动过程中没有考虑如何保距.此外,D-Privacy[18]机制结合空间位置之间的距离约束实现了空间范围与频率查询,然而该机制由于缺少空间索引而无法直接应用于近似kNN查询.目前,支持保距编码机制且满足本地化差分隐私的算法包括DPRL[5]与LSHPM[6].其中,DPRL算法结合BV[4]编码与Rappor[2]机制实现了字符串匹配,但该算法没有考虑字符串整个值域对匹配精度的影响;LSHPM算法利用LSH结构实现近邻查找时的保距性,然而该算法没有充分利用LSH结构特征来提高查找的碰撞概率.因此,针对文献[4-6]所提算法的不足,本文提出了2种基于局部敏感Hash结构的空间kNN查询算法,这2类算法不但能够适用于大规模空间数据,还能够比较精确地响应kNN近似查询.
2 定义与问题
2.1 本地化差分隐私
本地化差分隐私保护技术通常要求用户本地编码与扰动自己的数据,把扰动之后的数据汇报给收集者,从而使个人隐私不被泄露.本地化差分隐私的形式化定义如下所示.
定义1.ε-本地化差分隐私.给定一个随机算法M及其定义域Dom(M)和输出值域Range(M),若M在任意2条不同空间点pi与pj(pi,pj∈Dom(M))上得到相同输出结果O(O∈Range(M))的概率满足不等式:
Pr[M(pi)∈O]≤eε×Pr[M(pj)∈O],
(1)
则M满足ε-本地化差分隐私.其中,ε为隐私预算.
本地化差分隐私通常具有序列组合性质.
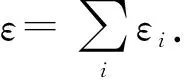
2.2 随机应答机制
随机应答机制[9]是实现本地化差分隐私的常用技术之一.该机制主要关注用户在响应敏感布尔问题时,通常以概率p真实应答,以1-p的概率给出相反的应答.收集者利用噪音结果对真实的统计结果进行估计分析.目前,基于随机应答机制出现了以GRR与按位扰动(BitP)为代表的本地扰动算法.
1) GRR[8]算法.给定空间点pi与pj,且pi,pj∈{1,2,…,d},其中d为值域大小,GRR算法为:
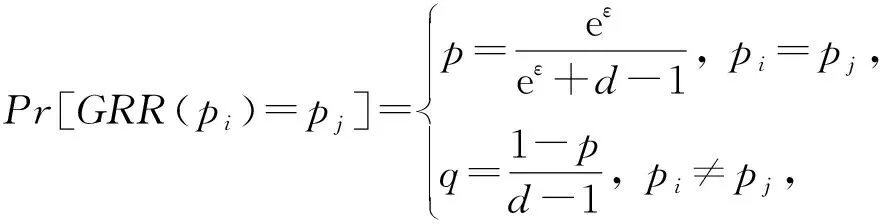
(2)
其中,e表示自然对数的底数,ε为隐私预算.
2) BitP[2]算法.给定空间点pi,利用0/1编码将其转换成二进制向量B.对于B中任意一个比特位Bi,BitP算法扰动为:

(3)

2.3 空间近似kNN查询
高效的索引结构是响应空间kNN查询的关键技术之一.以KD-树为代表的层次结构可以有效响应kNN查询.然而,在本地化差分隐私环境下构建KD-树比较困难与低效,其主要原因是构建该结构具有数据相关性,与具体的数据分布紧密关联.不同于KD-树,局部敏感Hash结构通过设计特殊的Hash簇,使得2个近邻空间数据点以较高的概率映射成相同的Hash值,而使2个距离比较远的空间数据点以较低的概率映射成相同的Hash值.该结构具有较强的保距性,其形式化定义为:
定义2.LSH[7].给定空间查询距离约束参数r与近似比率参数c,若Hash簇H对于空间中任意2个点pi与pj满足:
1) 若dis(pi,pj)≤r,则Pr[h(pi)=h(pj)]≥P1;
2) 若dis(pi,pj)≥cr,则Pr[h(pi)=h(pj)]≤P2.
则H被称为(r,cr,P1,P2)-敏感的,其中dis(pi,pj)表示pi与pj之间的距离,Pr[h(pi)=h(pj)]表示pi与pjHash值相等的碰撞概率,常量c>1,P1>P2.

因此,本文要解决的问题是在设计满足本地化差分隐私的空间kNN查询算法的同时,要尽可能获得精度较高的查询结果.
3 基于本地化差分隐私的近似kNN查询算法
在设计满足本地化差分隐私的空间近似kNN查询算法时需要考虑2条原则:1)所设计的本地编码与扰动算法尽可能满足保距性;2)所设计的kNN查询算法尽可能返回较高精度的查询结果.针对这2条原则,本文利用位置空间到汉明空间嵌入技术与本地敏感Hash技术对空间数据进行编码与Hash压缩,结合压缩编码设计相应的扰动算法.
3.1 汉明空间嵌入与LSH Hash压缩
由于汉明空间中容易找到合适的LSH Hash簇,每个用户对自己的位置pi(pi∈D)进行汉明空间转换.结合文献[7],本文提出了一种空间位置0/1编码算法,具体细节如算法1所示:
算法1.Embed.
输入:第i个用户的位置pi且pi∈D、D中所有经度与维度的最大值M;
输出:pi的汉明编码bi.

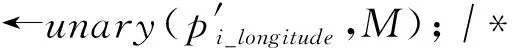
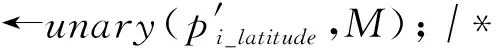

⑤ returnbi.
Embed算法的主要目的是对每个用户的空间位置进行0/1编码,进而形成二进串.例如M=3,pi=(1,2),则unary(bi1)=(100),unary(bi2)=(110),进而可知b的长度为6且bi=(100110).如果每个用户直接对长度为2M的0/1串扰动并报告给收集者,会破坏经纬度之间的关联性以及造成较高的通信代价.为此,本文利用具有保距性的LSH Hash簇对每个用户的0/1串进行压缩.LSH Hash压缩与kNN查询原理如图2所示:
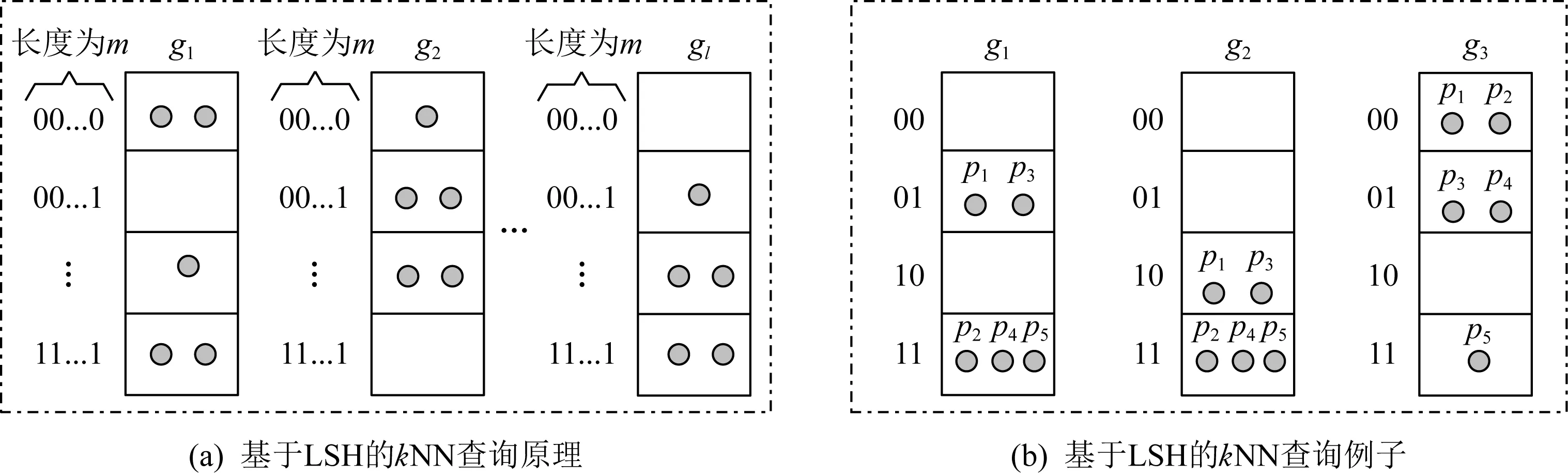
Fig. 2 Theory and example of LSH图2 LSH原理与例子
由定义2可知,满足条件1与条件2即可获得LSH Hash簇H.若汉明距离dis(pi,pj)≤r,则表示pi与pj近邻;dis(pi,pj)≥cr,则表示pi与pj不近邻.例如p1=(1,2),p3=(2,3).p1与p3的0/1编码分别为(100110),(110111).结合H与Hash表g1,如图2(b)所示,随机选择2个Hash函数h3与h4.利用h3和h4压缩p1与p3的编码,即可获得g1(100110)=01,g1(110111)=01.因此,p1与p3被Hash到g1的01编码所对应的桶内.
获得Hash簇H后,如何计算条件1与条件2中的P1与P2至关重要.根据Embed算法,碰撞概率P1与P2可以表示为
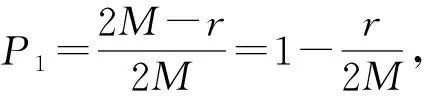
(4)

(5)
根据式(4)(5)可知,当参数r,M与c确定后,即可获得P1,P2.例如p1=(1,2),p3=(2,3),M=3,c=2,汉明距离r=dis(p1,p3)=2,则P1=2/3,P2=1/3.然而,合适的LSH Hash函数应该使P1尽量大且P2尽量小.结合文献[7]发现,通过增加Hash表个数l以及增加每个Hash表的Hash函数个数m,可以增大P1与P2之间的间隔,进而提高2个近邻点被Hash到同一个桶的碰撞概率.具体技术细节为:
结合图2(a),假设有l个Hash表,每个Hash表对应1个Hash簇H.从每个Hash簇H中随机抽取m个Hash函数,形成该Hash表的串型Hash函数,即gi={h1,h2,…,hm},1≤i≤l.则l个Hash表所对应的串型Hash函数表示为G={g1,g2,…,gl}.给定任意1个空间位置pi以及任意1个空间查询点q,利用拥有l个Hash表的Hash函数G表示pi与q之间的碰撞概率:
Pr[G(pi)=G(q)]= 1-[1-Pr[g1(pi)=g1(q)]]×…× [1-Pr[gl(pi)=gl(q)]]= 1-[1-(P1)m]l,
(6)
其中,Pr[gi(pi)=gi(q)]=(P1)m.
根据1-[1-(P1)m]l>(P1)m可知,多Hash表的碰撞概率明显高于单Hash表.
例如p1=(1,1),p2=(2,1),p3=(1,2),p4=(2,2),p5=(3,2).相应的0/1编码分别为(100100),(110100),(100110),(110110),(111110).设m=2,l=3,则G={g1,g2,g3},gi={h1,h2}.设g1,g2,g3分别抽取上述p1~p5的0/1编码的第2与第4个位置、第1与第2个位置、第3与第5个位置.则p1~p5这5个点分别在g1,g2,g3中的位置如图2(b)所示.给定查询点q=(3,3),相应的0/1编码为(111111).遍历g1,g2,g3可得p5是q的最近邻.
3.2 基于LSH的空间kNN查询算法
由文献[6]可知,当攻击者获得Hash函数{h1,h2,…,hm}后,可获取目标用户的隐私位置信息.因此,本文保护l个Hash表的构建过程,并遍历所有Hash表响应kNN查询.给定隐私预算ε,如何构建l个Hash表是个大挑战.本文分别利用隐私预算分割与用户分组策略设计了2种近似kNN查询算法.
3.2.1 基于隐私预算分割的kNN查询算法
本节首先基于多Hash表与多Hash函数的LSH结构提出PELSH算法,该算法包括本地汉明空间嵌入、用户位置本地扰动、收集者重构多Hash表结构以及响应kNN查询等操作.该算法具体细节为:
算法2.PELSH算法.
输入:n个用户的空间位置、查询点q、查询半径r、Hash表个数l、Hash函数个数m、隐私预算ε、经纬度最大值M;
输出:满足本地差分隐私的kNN集合S.
①S←∅;
② 收集者初始化l个Hash表{g1,g2,…,gl},每个gi包含m个Hash函数;
③ 收集者发送l个Hash表和m个Hash函数给每一个用户;
用户端:
④ for对每个Hash表gido
⑤ for每个用户i=1 tondo
⑥ 用户i把自身位置pi汉明嵌入为bi,bi←Embed(pi,M);
⑦ 用户i利用LSH对bi进行Hash压缩
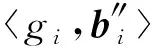
⑩ end for
收集者端:
PELSH算法利用隐私预算分割策略解决近似kNN查询问题.首先收集者创建l个空Hash表并共享给n个用户(步骤②③).每个用户利用Embed,LSH将自身数据转换与压缩成0/1串,利用LRR机制本地扰动压缩后的0/1串,并将扰动值报告给收集者(步骤④~).收集者结合所有用户的报告值重构每个Hash表,并利用重构之后的l个Hash表响应kNN查询(步骤~).
根据PELSH算法的步骤⑧可知,每个用户利用LRR算对压缩结果进行本地扰动.扰动后的0/1串直接决定着某用户位置的Hash桶地址.基于此,本文分别结合BitP机制与GRR机制设计2种本地扰动算法PELSHB与PELSHG,并利用PELSHB与PELSHG替换步骤⑧中LRR来扰动LSH压缩后的0/1串.2种算法的细节为:
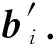
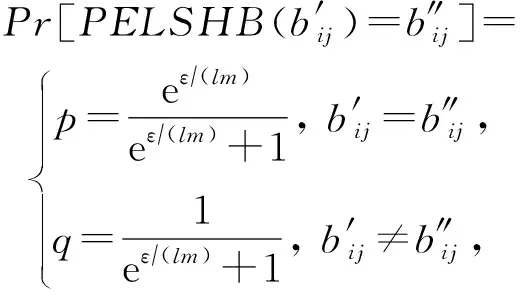
(7)
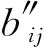
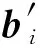
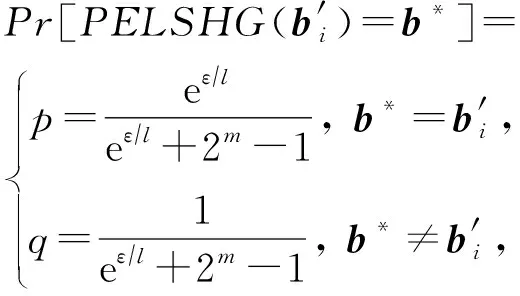
(8)
其中,b*表示值域2m中的任意值.
定理1.PELSHB算法与PELSHG算法满足ε-本地化差分隐私.
证毕.
尽管收集者采用PELSHB算法与PELSHG算法收集了n个用户的位置并重构了l个Hash表,但对于任意1个Hash表,我们期望它所对应的任意1个Hash桶中空间位置点计数满足无偏性.
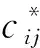
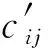
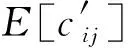
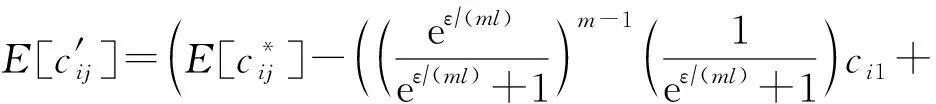
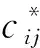
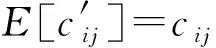
证毕.
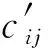
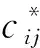

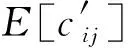
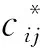
证毕.
定理4.利用PELSHB算法构建l个Hash表,

至少以概率1-β成立.
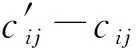

根据伯恩斯坦不等式可知:
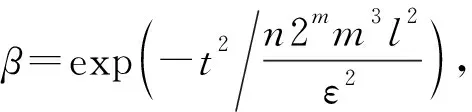
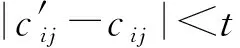
证毕.
定理5.利用PELSHG算法构建l个Hash表,
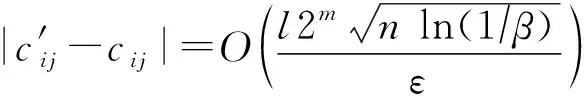
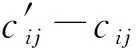

根据伯恩斯坦不等式可知:

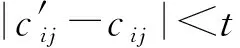
证毕.
由算法2可知,通过增加Hash表个数l和Hash函数个数m可以提升kNN查找的碰撞概率,如式(6)所示.然而,PELSH算法却是在分割隐私预算的前提下构建l个Hash表索引结构.若l值过大,则PELSHB算法与PELSHG算法会产生过大的误差.因此,本文结合用户分组策略来实现kNN查询.
3.2.2 基于用户分组的kNN查询算法
本节主要阐述PULSH算法的具体实现细节.
算法3.PULSH算法.
输入:n个用户的位置数据、查询点q、查询半径r、Hash表个数l、Hash函数个数m、隐私预算ε、经纬度最大值M;
输出:满足本地差分隐私的kNN集合S.
① 与算法2的步骤①~③相同;
② 把n个用户随机分成l组,分别记为C1,C2,

用户端:
③ for每个Hash表gi(1≤i≤l) do
④ for对Cj中的每个用户do
⑤ 与算法2的步骤⑥⑦相同;
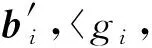
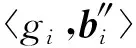
⑧ end for
⑨ end for
收集者端:
⑩ for每个Hash表gido
PULSH算法核心思路是利用用户分组策略重构l个Hash表.首先是对n个用户进行随机均匀分组(步骤②).每个用户利用LRR机制扰动LSH压缩后的0/1串,并将扰动值发送给收集者(步骤⑥⑦).收集者结合所有用户的报告值重构每个Hash表,并响应kNN查询(步骤⑩~).
根据PULSH算法的步骤⑥可知,如何利用LRR扰动0/1串是该算法的关键.类似于PELSH算法,本文同样结合BitP机制与GRR机制设计2种扰动算法PULSHB与PULSHG,并用这2种算法替换步骤⑥中的LRR.
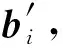
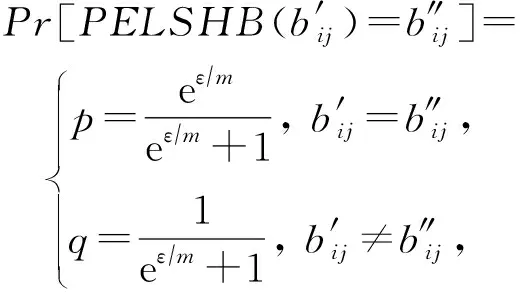
(9)
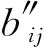
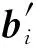

(10)
其中,b*表示值域2m中的任意值.
定理6.PULSHB算法与PULSHG算法满足ε-本地化差分隐私.
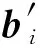
证毕.
收集者利用PULSHB与PULSHG算法重构l个Hash表,并结合重构的Hash表响应kNN查询.类似于PELSHB与PELSHG算法,对于任意1个Hash表,它的任意1个Hash桶中位置点计数应满足无偏性.
定理7.n个用户的位置点经过PULSHB算法处理后,分布在l个Hash表中.对应任意1个Hash

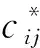
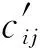
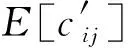
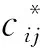
证毕.

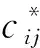
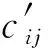
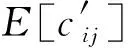
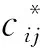
证毕.
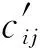
至少以概率1-β成立.
根据伯恩斯坦不等式可知:


证毕.
至少以概率1-β成立.
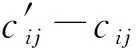
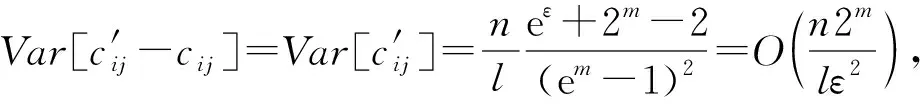
根据伯恩斯坦不等式可知:

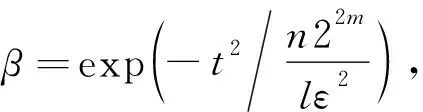
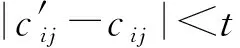
证毕.
3.2.3 4种本地扰动算法的优劣分析
定理1~10分别估计了每个桶计数的无偏性与最大偏差.下面分析PELSHB,PELSHG,PULSHB,PULSHG彼此的优劣.设Error(PELSHB),Error(PELSHG),Error(PULSHB),Error(PULSHG)为各自的最大偏差.隐私预算分割策略下的算法为PELSHB与PELSHG;用户分组策略的算法为PULSHB与PULSHG.
1) 基于隐私预算分割与用户分组的算法对比.

(11)
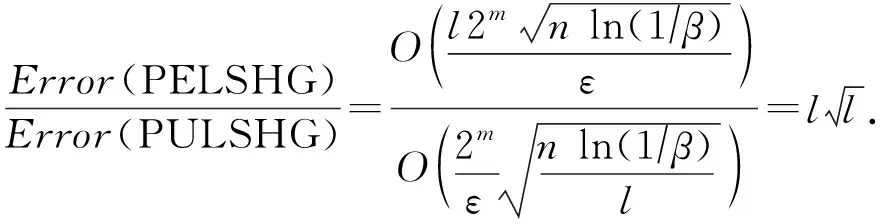
(12)
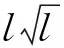
2) PULSHB和PULSHG、PELSHB和PELSHG对比.
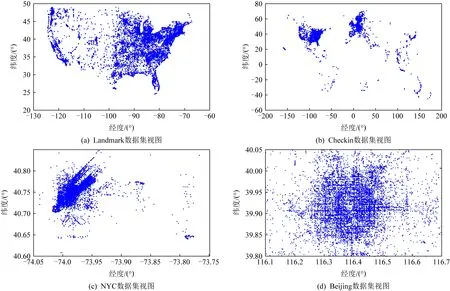
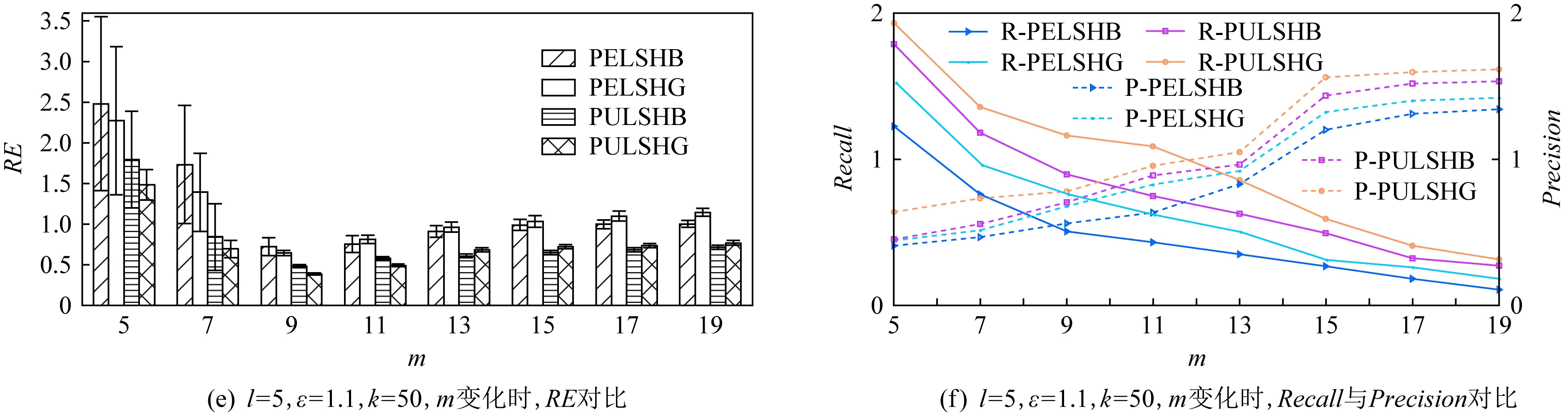
根据式(13)(14)可知,当Hash表中Hash函数的个数m<10时,Error(PULSHB)>Error(PULSHG),Error(PELSHB)>Error(PELSHG).然而,当Hash函数个数m≥10时,Error(PULSHB) (13) (14) 实验平台是4核Intel CPU(4 GHz),8 GB内存,Win7系统,代码采用Python实现.实验采用4个数据集,分别为Landmark数据集、Checkin数据集、NYC数据集以及Beijing数据集.其中Landmark数据集从infochimps平台获得,记录了2010年人口普查时用户到过的美国48个州的地标位置,总共包含870 051条数据;Checkin数据集从基于地理位置的社交网站Gowalla获取,记录了在2009-02—2010-10期间用户签到的时间和位置信息,包含100万条记录;NYC数据集是2011年整个12个月内纽约市出租车的乘车和下车的地理坐标数据,包含1 000万条信息;Beijing数据集是2011年2月某一周内北京市10 357辆出租车的乘车和下车地理坐标数据,包含1 500万条信息.4种数据集具体细节与可视化结果分别如表1与图3所示: Table 1 Characteristics of Datasets表1 数据集的属性 结合4个数据集,采用相对误差(relative error,RE)、召回率(Recall)、精度(Precision),度量HammingP,DPRL,LSHPM,PELSHB,PELSHG,PULSHB,PULSHG这7种算法的查询精度,其中HammingP是把位置数据嵌入到汉明空间后直接进行比特扰动的算法.隐私参数ε的选取分别为0.1,0.3,0.5,0.7,0.9,1.1.为了便于实验图的展示,我们对RE,Recall,Precision的实验结果取对数,并且加上最大偏移量.在4.1节中,本文提出的4种算法参数设置为l=5,m=9;4.2节和4.3节中,l=5. Fig. 3 Visualization of four datasets图3 4个数据集的可视化结果 Fig. 4 Comparisons on Landmark图4 基于Landmark数据集的算法对比 Fig. 5 Comparisons on Checkin图5 基于Checkin数据集的算法对比 Fig. 6 Comparisons on NYC图6 基于NYC数据集的算法对比 结合4种数据集,固定参数l与m,改变ε,对7种算法进行性能对比分析.图4(a)~图4(c)、图5(a)~图5(c)、图6(a)~图6(c)和图7(a)~图7(c)描述了HammingP,DPRL,LSHPM,PELSHB,PELSHG,PULSHB,PULSHG算法的RE,Recall,Precision的比较结果.当k=50时,随着ε的增加,所有算法的RE值均呈下降趋势,Recall和Precision呈上升趋势,原因是噪音的多少与ε成反比,ε越大,RE越小,Recall和Precision越高.例如,在Landmark数据集上,PELSHB,PELSHG,PULSHB,PULSHG算法均优于其他3种算法.在ε=1.1时,HammingP和DPRL算法的RE是PULSHG算法的近10倍;LSHPM算法的RE是PULSHG算法的近4倍;PULSHG的Recall是HammingP,DPRL,LSHPM算法的近20倍,Precision是这3种算法的近3倍.此外,相比HammingP和DPRL算法,本文采用LSH对数据进行压缩转换,使其在具有保距性的前提下,减小隐私预算分割的次数,增加Recall与Precision;相比LSHPM算法,本文提出的4种扰动算法增加了相似数据的碰撞概率,提高了查询精度. 图4(d)、图5(d)、图6(d)和图7(d)描述了HammingP,DPRL,LSHPM,PELSHB,PELSHG,PULSHB,PULSHG算法随着近邻个数k的增加导致RE值的变化情况.由实验结果可以发现,当ε=1.1时,随着近邻个数k从10增加到110,RE呈现先减少后增加的趋势,其原因是查询的近邻位置越多,查询的范围越大,包含的查询单个点数越多,累计误差越大,导致精度随着查询范围的增大而降低.当k=50时,在4个数据集上,PULSHG算法最优.在Checkin数据集上,PULSHG算法RE值是HammingP和DPRL算法的近90倍,是LSHPM的15倍,用户分组相比于隐私预算分割方法精度提高近5倍. 图4(e)(f)、图5(e)(f)、图6(e)(f)和图7(e)(f)描述了算法PELSHB,PELSHG,PULSHB,PULSHG的RE,Recall,Precision的比较结果.由图(e)可以发现,随着Hash函数的个数m的增加,RE值先降低后增加,其中m<10时PELSHG优于PELSHB,m≥10时PELSHG的误差大于PELSHB.用户分组算法的临界点为m=12.在m<12时,PULSHG优于PULSHB;在m≥12时,PULSHG的误差大于PULSHB.按照Hash地址扰动方法的误差随着Hash函数个数的增加呈指数形式增加.m=12与3.2.3节的理论分析存在一定出入,其原因是PULSHB与PULSHG最大偏差理论分析与参数l无关,而具体实验过程与l相关.从图4(f)、图5(f)、图6(f)和图7(f)中可以发现,PELSHB,PELSHG,PULSHB,PULSHG算法的Recall(R-PELSHB,R-PELSHG,R-PULSHB,R-PULSHG)与Precision(P-PELSHB,P-PELSHG,P-PULSHB,P-PULSHG)为负相关关系,Recall均下降,Precision均上升.从整体来看,用户分组的算法优于隐私预算分割,其原因是用户分组情况下每个用户的ε是隐私预算分割情况下的l倍,ε越小误差越大,其对应的Recall与Precision越低. 本文针对本地化差分隐私保护下空间kNN近似查询存在的问题,结合现有0/1编码机制与扰动机制存在的不足,提出了基于LSH结构的kNN近似查询算法.该类算法通过汉明空间嵌入、LSH Hash压缩、隐私预算分割与用户分组等策略实现了空间数据高精度收集.从本地化差分隐私定义角度分析文中所提出的算法满足ε-本地化差分隐私.最后通过4种真实的空间数据集验证了本文算法的kNN近似查询精度.实验结果表明,本文算法明显优于现有的同类方法.未来工作考虑如何结合本地化差分隐私与LSH实现高维数据空间中的kNN查询问题. 作者贡献声明:张啸剑负责论文的算法设计、相关定理设置及论证,并负责整篇论文的撰写;徐雅鑫负责论文算法的实现与实验结果分析;孟小峰指导论文撰写的逻辑性与算法的合理性.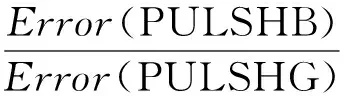
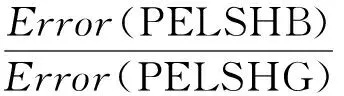
4 实验结果与分析



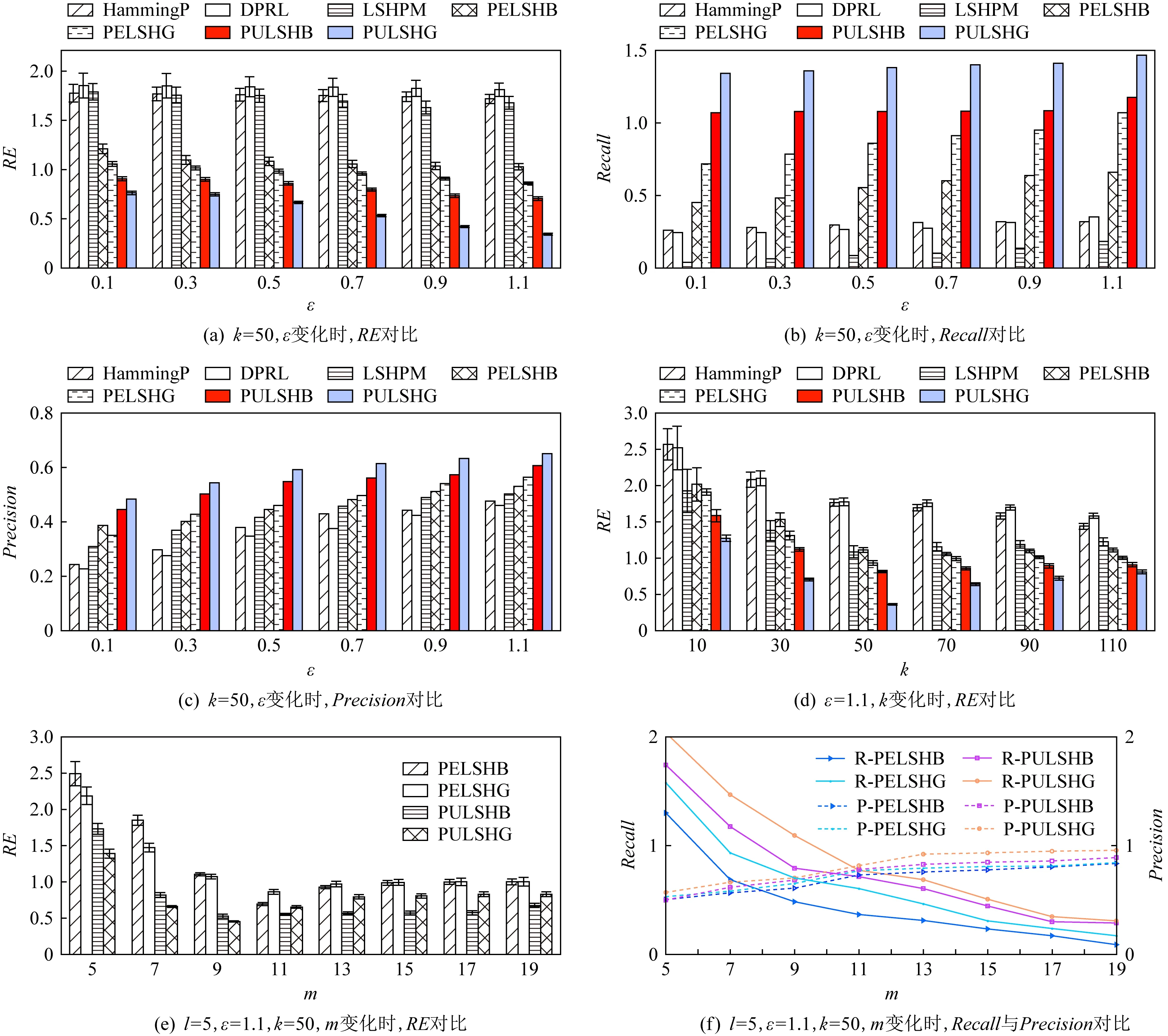
4.1 基于ε变化的7种算法性能比较
4.2 基于k变化的7种算法性能比较
4.3 基于m变化的7种算法性能比较
5 结束语

