多尺度梯度对抗样本生成网络
石 磊 张晓涵 洪晓鹏,2 李吉亮 丁文杰 沈 超
深度神经网络(Deep Neural Networks, DNNs)的成功推动计算机视觉领域各类工作的迅速发展,行人重识别(Person Re-identification, ReID)任务就是其中的典型代表.近来有研究表明,深度ReID模型依旧继承深度神经网络的脆弱性,即DNNs的输出容易受到对抗扰动的影响,遭受对抗性攻击[1-2].
近年来,研究者们针对ReID模型的对抗攻击开展一系列研究,设计攻击算法生成对抗样本[1-5]攻击ReID模型,从而充分测试模型和系统的脆弱性,并为提升和强化系统的鲁棒性提供参考.此外,由于ReID模型本身会使用如ResNet50[6]、Dense-Net121[7]、VGG16[8]、SENet154[9]、ShuffleNet[10]和TransViT(Transformer ReID Vision Transformer)[11]等基于卷积神经网络(Convolutional Neural Network, CNN)和变形器网络(Transformer)架构[12]的骨干网络,攻击算法对ReID模型进行验证的同时也对这些骨干网络进行验证,对相关领域的研究同样也会产生促进作用.
通常ReID被定义为一个排序问题,而不是分类问题[4].因此对ReID模型的攻击不同于对分类模型的攻击,在构造对抗样本时,大部分分类模型的攻击方法,如通过降低预测概率回传梯度的FGSM(Fast Gradient Sign Method)[13]等,直接攻击ReID模型时会受到限制.要实现ReID模型的攻击,需要研究如何扰乱模型最终的输出排序.Zheng等[14]提出ODFA(Opposite-Direction Feature Attack),使用特征逆向攻击法攻击目标检索模型,在特征空间中,将对抗样本特征推向与原始特征相反的方向,达到扰乱图像检索深度排序结果的目的. Bai等[1]提出AMA(Adversarial Metric Attack),直接在注册集(Gallery)中添加对抗扰动,并设计攻击距离度量,直接破坏成对图像之间的距离,大幅降低ReID系统的准确性,达到攻击ReID模型的目的.此后,Wang等[2]提出TCIAA(Transferable, Controllable and Inconspicuous Adversarial Attacks),使用对抗公式优化生成能扰乱排序输出的对抗样本,方法倾向于最小化非匹配对(即待匹配对象(Probe)与负样本)的距离,同时最大化匹配对(即待匹配对象(Probe)与正样本)的距离.Ding等[4]提出MUAP(More Universal Adversarial Perturbation),引入平均精度(Average Precision, AP)的近似值,设计基于AP的样本序列损失函数,有效扰乱全局排序关系,并生成具有更强的白盒和黑盒攻击能力的通用对抗扰动[15].
考虑到对注册集的访问极其困难,AMA在实际场景中的应用受到很大限制.其它代表性ReID攻击算法,如TCIAA、MUAP等,也存在如下缺陷.ReID对抗攻击通过对模型的输入样本图像加入精心设计的轻微扰动,诱导模型得出偏离真实的排序结果,这种扰动通常要求非常微小,无法被人类视觉系统轻易察觉.这就给攻击设置条件瓶颈.一方面,MUAP生成的通用对抗样本过于单一,固定的对抗样本对于鲁棒性研究分析而言显然是不够全面的.另一方面,在设定基于范数的扰动样本能量上限后,TCIAA在较低的攻击能量[16]条件下攻击性略显不足.此外,被攻击图像的视觉质量,即生成的对抗样本与原始图像之间的结构相似度(Structural Similarity, SSIM)[17]也有待提高.
生成对抗网络(Generative Adversarial Network, GAN)自提出以来,已成为图像生成领域的热门方法[18].GAN具有较好的学习生成复杂数据分布的能力,因此具有广泛的应用场景,相关的衍生模型在图像生成、超分辨率、风格转换等应用中都取得快速进展.但原始的GAN难以生成高分辨率图像,需要性能更强的改进策略.为此,研究者们提出性能更强的GAN[19-21].然而,GAN训练不稳定的现象已成为共识[20],由于训练期间不稳定和对超参数的敏感,GAN很难适应不同的数据集.对于这种训练不稳定的现象,一种普遍的观点是:当真实分布和生成分布的支撑集重叠程度较低时,GAN中鉴别器反馈给生成器的梯度无法提供有益的信息.为此,Karnewar等[21]提出MSG-GAN(Multi-scale Gradients for GAN),研究使用多尺度梯度生成高分辨率的图像.不同于渐进式图像生成技术[22],MSG-GAN能达到一个较好的分布匹配,在梯度回传训练过程中,将梯度传递到所有尺度,不断强化真假数据分布重叠,使网络注重学习更精细的细节,从而获得既定输出.相比传统的GAN,MSG-GAN具有更强的优势.
鉴于MSG-GAN在生成样本质量上的优势, 本文提出多尺度梯度对抗样本生成网络(Multi-scale Gradient Adversarial Examples Generation Network, MSG-AEGN),采用多尺度的网络结构,获得不同语义级别的原始样本输入和生成器中间特征.利用注意力调制模块将生成器中间特征转换成多尺度权重,对原始样本像素进行调制以获得对抗样本.在此基础上,提出基于图像特征平均距离和三元组约束的改进型对抗损失函数,约束和引导MSG-AEGN的训练.在实验部分,选择3个主要的ReID基准数据集Market1501[23]、CUHK[24]、DukeMTMC-reID[25]验证MSG-GAN的有效性,并与TCIAA、MUAP进行对比分析.结果表明,MSG-GAN能生成能量较低、攻击性较强、结构相似度较高的对抗样本,并在多个行人重识别数据集上均取得较优的攻击性能.
1 多尺度梯度对抗样本生成网络
本文提出多尺度梯度对抗样本生成网络(MSG-AEGN),将注意力机制引入多尺度生成器结构中,生成高质量对抗样本.
1.1 模型总体结构
MSG-AEGN的总体结构如图1所示.模型主体包括注意力调制的多尺度对抗样本生成器Gadv,对抗样本判别器Dadv和目标模型T.
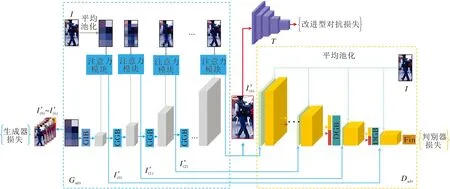
图1 MSG-AEGN总体框架图Fig.1 Framework of MSG-AEGN
MSG-AEGN分别从生成器端和判别器端传入多尺度的原始图像信息,从低分辨率4×2的图像一直到高分别率256×128的图像,这些多尺度的样本Ii(i=0,1,…,6)由平均池化(AvgPooling)运算而来,并随着训练的进行不断更新网络参数,最终学习生成256×128的对抗样本.生成器Gadv由注意力模块(Attention)、生成器初始模块(Generator Initial Block, GIB)和生成器生成模块(Generator Gene-ration Block, GGB)组成.注意力模块[7]主要实现两个功能:1)负责将生成器中间特征通过1×1卷积降维运算转换成多尺度权重Wi,2)使用Wi对原始样本Ii进行调制,得到多尺度对抗样本I′i.目标模块T主要负责提取特征,用于计算改进型对抗损失,生成器受到生成器损失和改进型对抗损失约束,判别器受到判别器损失约束.对抗样本判别器Dadv由判别器生成模块(Discriminator Generation Block, DGB)和最终输出模块(Final Block, Fin)组成,用于判别对抗样本的真实性(即与原始样本的接近度).
图2进一步描述各组成模块的实现细节及生成器Gadv和判别器Dadv之间的信号传递,包括生成器Gadv和判别器Dadv的每步具体实现及网络训练过程中每个尺度的维度变换.GIB、GGB、DS(Down Sam-ple)、HD(High Dimension)、Fin由不同的运算组合而成,线性激活单元由1×1卷积降维实现,Mini-batchstDev(Minibatch Standard Deviation)[22]为鉴别器的Batch标准偏差层(为了提高生成器模型生成数据的多样性,在判别器的最后一层上加入mini-batch discrimination).谱归一化(Spectral Normali-zation, SN)[26]和批归一化(Batch Normalization, BN)[27]是为了稳定GAN的训练,对数据分布进行归一化.
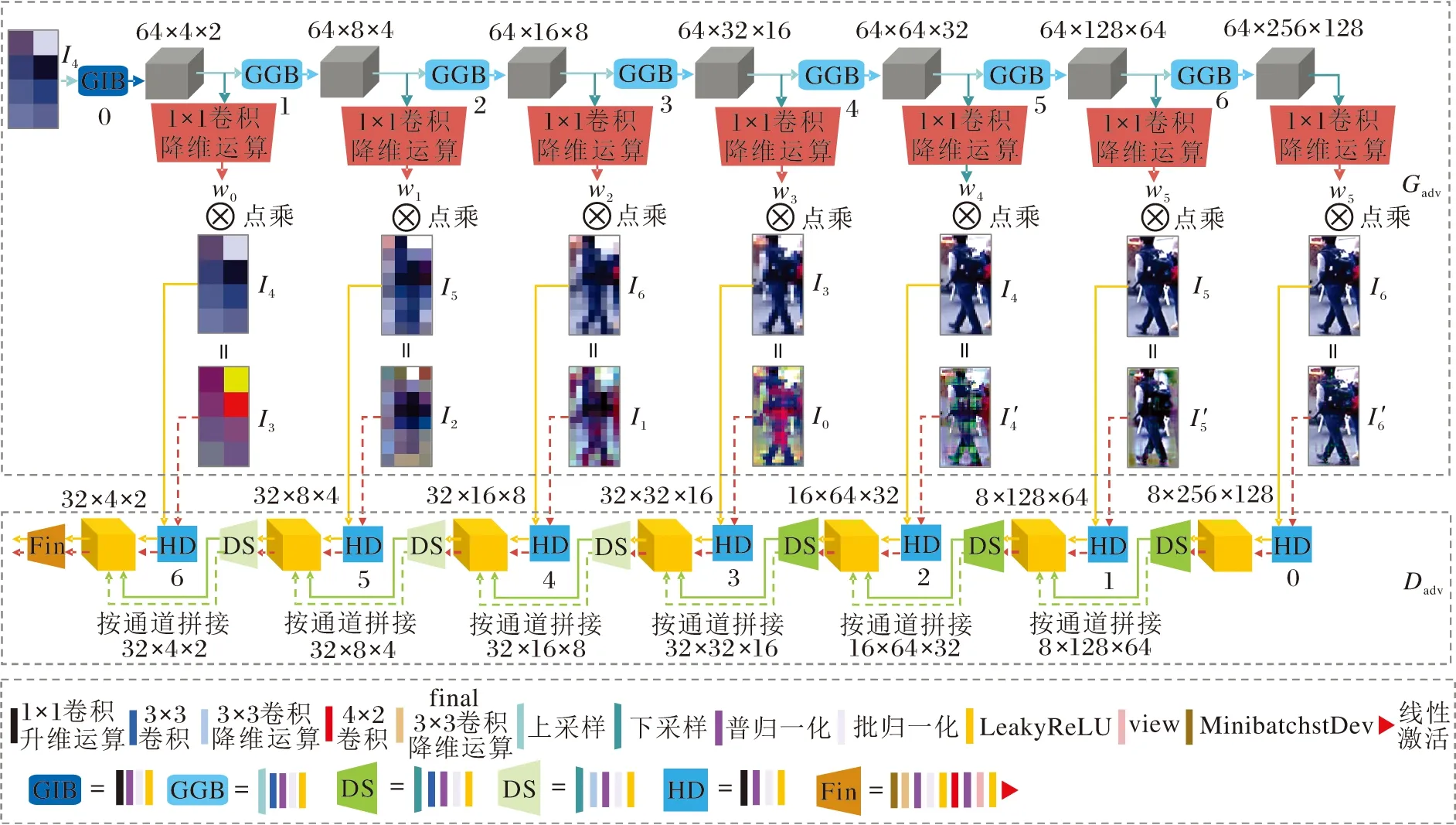
图2 MSG-AEGN各模块细节图Fig.2 Details of each module of MSG-AEGN
原始图像I由池化操作可获得多个尺度(不同分辨率)的图像Ii,i=0,1,…,6,注意力调制模块负责将每个尺度的图像与权重Wi点乘,得到多尺度对抗样本I′i,并将多尺度对抗样本I′i送入判别器进行真假判别训练,提高判别器的判别能力.同时多尺度生成器需要生成更高相似度的对抗样本以欺骗判别器.最后,将I′6送入目标网络T提取全局特征,计算改进型对抗损失.
为了便于观察生成器注意力调制模块的多尺度运算过程,本文将其结果可视化,如图3所示.图中灰色箭头表示平均池化获得多尺度原始样本方向,黄色箭头表示单个像素感受野[27]减小方向,图像中每个方形表示一个像素,随着分辨率升高,伴随像素增加,单个像素点方框越模糊.
在原始样本中灰色箭头所指平均池化方向上,感受野逐渐增大,单一像素点控制的感受野呈倍数增加,细节层语义更丰富,抽象层语义更抽象.只有浅层语义和深层语义结合才能充分表示原始图像的完整语义信息,这也说明4×2分辨率的重要意义.4×2分辨率表示原始样本的抽象层语义,在4×2分辨率中的绿框区域,伴随分辨率递增,像素数量逐渐增加,而行人书包上的语义要素也逐渐清晰.同样,在对抗样本生成过程中,注意力调制的多尺度生成器在深层对原始样本施加的调制更明显,在红框区域沿分辨率递增的方向上,对原始样本的调制逐渐减弱,这是因为在原始样本抽象层语义中,多尺度对抗样本生成网络学习到影响目标模型精度的抽象层权重,如果减少网络尺度,会使网络学习不到大感受野下由注意力模块产生的权重,从而导致在细节层网络需要付出更高的攻击能量代价,直接导致生成的对抗样本视觉质量降低.因此,相比多尺度网络,单尺度网络生成的对抗样本扰动能量会增加,SSIM值会减小.

(a)多尺度原始图像像素增加过程(a)Incremental process of multi-scale original image pixels
同一行人在不同姿态下多尺度对抗样本生成的可视化结果如图4所示.由图可清晰看到,即便是同一行人,在不同姿态和微弱的外部环境变化下,生成器生成的权重对原始样本的调制(见右侧红色方框内容)都会随之改变,这也验证MSG-AEGN学习到不同尺度的权重信息.
对抗度量部分主要通过目标网络T(被攻击的ReID网络)提取全局特征,用于计算对抗损失[2],引导网络向错误的排序方向训练.
总体而言:框架设计原则遵循MSG-GAN的网络特性,有利于对抗样本生成网络在不同感受野下提取更关键的特征信息;同时多尺度生成器Gadv学习深层样本中影响度量精度的关键权重,并获得攻击能量更低的对抗样本.

(a)原始样本 (b)对抗样本(a)Original examples (b)Adversarial examples图4 不同姿态多尺度可视化结果Fig.4 Multi-scale visualization of different poses
1.2 对抗样本生成器
在MSG-AEGN中,对抗样本生成器记为Gadv,对应的初始化函数(见图2生成器0号模块)记为
其中A0∈R64×4×2.
此函数分为3步运算:1)采用1×1卷积升维运算,2)执行谱归一化和批归一化运算,3)使用LeakyReLU[28]激活单元执行激活操作.
本文设定初始化空间A-1∈R3×4×2由原始样本空间(数据集)经平均池化操作生成(即图2中I0),a-1∈A-1.生成器初始化模块定义为Γ0运算,则
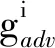
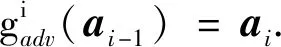
1.3 注意力调制模块
注意力调制模块分为权重转换模块和权重施加模块.权重转换模块将多尺度特征转换为注意力权重,权重施加模块利用生成的权重调制原始样本生成对抗样本.
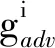
ζi∶Ai→Wi,
可得
ζi(ai)=wi,
其中,ai∈Ai,i=0,1,…,6.
换言之,wi是由生成器第i层模块gi的输出图像经过转换器ζi转换后的权重.ζi可看作是权重生成器,在生成器的不同阶段,要求学习到的特征映射能直接投影到不同尺度的权重空间.
给定任意输入的原始图像,其对应的多尺度空间表示为Ii∈R2i+2×2i+1×3.令操作⊗为矩阵点乘运算(对应位置相乘),则注意力调制机制利用权重wi对样本特征Ii进行调制,得到第i个尺度对应的对抗样本输出:
I′i=wi⊗Ii.
那么对抗扰动[6]生成表达为
pi=I′i-Ii,
其中,ai∈R2i+2×2i+1×3,pi∈R2i+2×2i+1×3,i=0,1,…,6.
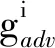
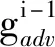
x6=Gadv(a-1).
除了得到最终的样本输出x6=I′6,生成器还可得到一系列不同尺度的中间结果xi=I′i,i=0,1,…,6,它将作为判别器的输入参与生成对抗学习.
1.4 对抗样本判别器

将不同尺度的样本送入判别器对应层,获得相应尺度的卷积激活体.为了简化表示,这里使用vi表示原始样本(真)或对抗样本(假)经过AF函数(图2中HD1~HD6模块)产生的卷积激活体(图2中黄色正方体),即
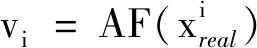
这里真假样本流向分别对应图2中黄色虚线箭头和红色虚线箭头,于是有
vi=AF(Ii)或vi=AF(I′i).
在此基础上定义函数φ,用于结合判别器第j个中间层尺度生成的vj与第j-1个中间层的输出:
φ[1-6](x1,x2)=[x1∇x2],
其中,x1、x2表示输入变量,[·∇·]表示空间叠加下采样运算,即第1步卷积激活体和前一层传入的激活量进行拼接运算(concat),第2步送入DG模块进行下采样运算.
除d0以外(该层运算缺少下采样运算,不涉及φ函数),定义判别器其余中间任意第j层的输出激活量q′j(函数φ的输出,即图2中DG模块输出量)为
q′j=φj(vj,q′j-1),
且j≠0(d0除外),于是
dj∶φj(vj,q′j-1)→q′j,
则有q′j=φ(vK-i,q′j-1).
由于i和j总是相互关联的,可通过j=K-i(K=6)关联生成器输出和判别器输入,那么
φj(vK-i,q′j-1)=[vK-i∇q′j-1],
于是,最终判别器方程为:
Dadv(v0,v1,…,vK-1,x′)=d0(x′)〉d1(vK-1,∘)〉…
dK-1(v1,∘)〉dK(v0,∘)〉dcs,
其中,运算∘表示前一个判别器模块的输出结果,运算 〉表示通道级联.x′=I′i表示多尺度原始图像,x′=Ii表示多尺度对抗样本,分别送入Dadv计算判别得分,该得分用于计算最终判别器损失函数.
1.5 损失函数
网络训练的目标是为了尽可能生成与原始图像接近且对目标ReID模型具有误导性的对抗样本.既要求对抗样本与原始图像尽可能逼近,也要求对抗样本中的对抗扰动能量尽可能小,还要对抗样本具有较强攻击性,因此本文使用生成器损失函数、判别器损失函数、改进型对抗损失函数和能量抑制损失函数训练网络模型.
1.5.1对抗损失
为了便于对比分析,本文对TCIAA[16]中使用的对抗损失函数重新进行描述.该损失函数趋向于使不匹配对距离(与负样本的距离)最小化,同时使匹配对距离(与正样本的距离)最大化.值得注意的是,如果反过来使不匹配对距离(与负样本的距离)最大化,同时使匹配对距离(与正样本的距离)最小化,会使模型性能提升,攻击的思路是使这种趋势逆向,对抗损失函数就是结合ReID常用三元组损失函数(Tripletloss)[29]的逆向思维设计的.
对抗损失为:
(1)
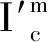
1.5.2改进型对抗损失函数
改进型对抗损失和对抗损失函数一样可攻击预测的排序,进而干扰系统的输出结果,并能增强模型的攻击性能.如图5所示,改进型对抗损失函数让MSG-AEGN学习到更倾向于负样本的错误排序,拉近待匹配对象(Probe)样本与负样本的相对距离,推远与正样本的相对距离,同时也拉近与负样本之间的绝对距离,从而使生成器G生成的对抗样本具有误导性.
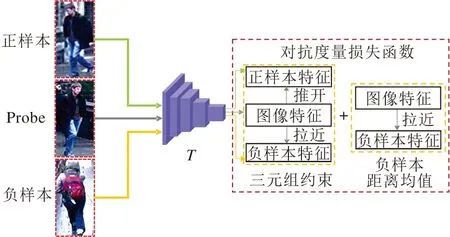
图5 改进型对抗损失函数计算原理图Fig.5 Calculation principle diagram of improved adversarial metric loss function
改进型对抗损失函数定义为基于三元组损失函数和图像特征距离的均值的计算度量:
LAdv-TripletLoss-IMP=(ha,--ha,++α)++ha,-,
其中,ha,+表示待匹配对象(Probe)与正样本之间基于全局特征距离总和的平均,ha,-表示Probe与负样本之间基于全局特征距离总和的平均,则有
LAdv-TripletLoss-IMP=max(0,ha,--ha,++α)+ha,-,
其中α为阈值,则
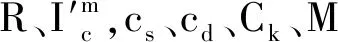
有研究表明,对抗损失函数适合ReID问题,甚至可能适合所有的开集问题.错误排序损失的使用也可能有利于攻击者学习一般的特征和可转移的特征,而设计这样的损失函数能更好地应用到基于GAN的网络结构中[16].不同于MUAP中一个Batch只能生成同种类型对抗扰动的方法,改进型对抗损失函数可帮助不同数据生成不同的对抗样本,进而得到多样化的对抗样本,更有利于鲁棒性测试.
1.5.3能量抑制损失函数
能量抑制损失函数使模型尽可能地抑制对抗样本中对抗扰动的能量大小,使模型使用更低的能量获得更高的攻击收益,并保证生成的对抗样本与原始图像的SSIM更高.定义能量抑制损失函数:
其中:给定BatchB,I∈B为B中一个输入图像,I′为对应的对抗样本;N=|B|为BatchB的尺寸,即图像总数;Normp为向量的p范数,本文实验中选用2范数.
1.5.4GAN损失函数
多尺度GAN要求生成器Gadv尽可能生成逼真样本,对抗样本判别网络Dadv尽可能增强判别能力以判别该样本是否为真实样本.那么,定义GAN总损失如下:
LM-GAN=GLoss+DLoss,
其中,GLoss表示生成器损失,DLoss表示判别器损失,
(2)
real_loss表示判别器对真样本判别损失,fake_loss表示判别器对假样本判别损失.判别器损失DLoss可定义为对真样本判别损失和对假样本判别损失的均值,于是有
real_loss=BCELoss[Sigmoid(r_preds),1(N)],
fake_loss=BCELoss[Sigmoid(f_preds),0(N)],
(3)
其中,
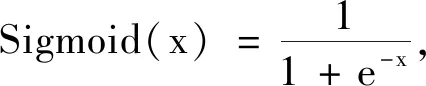
N=|B|表示BatchB中的样本数,1(N)函数表示生成N维全1向量,同样0(N)函数表示生成N维0向量.判别器对真样本(原始样本)的预测概率得分记为Sigmoid(r_preds),real_loss用于计算判别器对真样本的预测概率得分与1之间的差距损失,而判别器的理想状态是始终能将真样本判别为1.判别器对假样本(对抗样本)的预测概率得分记作Sigmoid(f_preds),fake_loss用于计算每个样本的预测概率得分与0之间的差距,而判别器的理想状态是始终能够将假样本判别为0,那么有
r_preds=D(Ii),f_preds=D(I′i),
(4)
其中,D(·)函数表示多尺度判别器Dadv,r_preds表示判别器输出真样本的预测中间量(这里原始样本Ii视作真样本),f_preds表示判别器输出假样本的预测中间量(这里对抗样本I′i视作假样本).定义
(5)
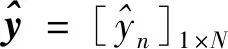
BCELoss[Sigmoid(D(I′i)),0(N)]}.
同上,生成器损失
GLoss=BCELoss[Sigmoid(g_preds),1(N)],
g_preds=D(I′i),
那么
GLoss=BCELoss[Sigmoid(D(I′i)),1(N)],
则有MSG-AEGN的总损失函数:
L=GLoss+DLoss+LAdv_TripletLoss_M+Lp.
2 实验及结果分析
2.1 实验数据集
本文在3个行人重识别数据集Market1501、CUHK03、DukeMTMC-reID上进行实验.Market1501数据集包含1 501个不同身份(ID)和32 688个标注框(Bounding Boxes),训练集包含12 936幅图像,751个ID,测试集(Query)包含3 368幅图像,750个ID,注册集(Gallery)包含15 913幅图像,751个ID.CUHK03数据集包含1 467个ID,28 192个边界框,训练集包含7 365幅图像,767个ID,测试集包含1 400幅图像,700个ID,注册集包含5 332幅图像,700个ID.DukeMTMC-reID数据集从视频中每120帧采样一幅图像,得到36 411幅图像.一共有1 404个人出现在至少两个摄像头下,有408个人(Dis-tractor ID)只出现在一个摄像头下.训练集包含16 522幅图像,702个ID,测试集包含2 228幅图像,702个ID,注册集数据包含17 661幅图像,1 110个ID.具体数据集信息如表1所示.
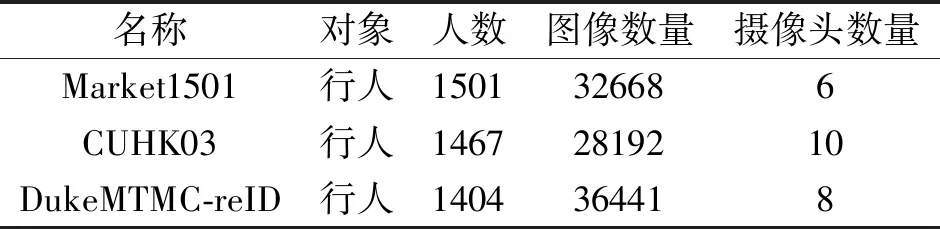
表1 实验数据集统计信息Table 1 Statistics of experimental datasets
2.2 实验细节
对于MSG-AEGN,输入图像大小为 256×128,使用随机翻转和随机擦除[29]进行数据增强.目标ReID网络选择相应的骨干网络.生成器和判别器都选择自适应矩估计(Adaptive Moment Estimation, Adam)[30]优化器,一阶矩估计的指数衰减因子β1=0.9,二阶矩估计的指数衰减因子β2=0.999,学习率为0.003,能量抑制函数中超参数λ1=λ2=0.5(攻击不同的模型需要微调),改进型对抗损失阈值α=0.3.在训练过程中,批大小设置为32,迭代次数设为10.每个批次中包含8个ID,每个ID有4幅图像.
实验遵循TCIAA中关于能量限定的协议[2],对比实验中设定对抗样本的范数能量范围(通过限定MUAP和TCIAA中扰动样本能量上限值实现).所有实验均在2块英伟达TITAN XP GPU上进行.
2.3 评价指标
本文选择使用如下评价指标:平均准确率均值(Mean Average Precision, mAP)和Rank-1,用于衡量攻击对ReID模型性能的影响.使用扰动样本的1范数能量大小(L1范式)表示攻击能量大小,对抗样本和原始样本的SSIM指标衡量两者的相似度,SSIM值越大表示生成对抗样本与原始图像越相似.在不考虑对抗样本和原始图像的结构相似性和对抗扰动能量大小前提下,只要给予对抗样本足够的攻击能量,就可以让ReID模型失效.很显然这样的做法与对抗攻击提出的微弱扰动不相符,在实际场景中容易被察觉,对于模型攻击和鲁棒性研究缺乏实际意义.对抗攻击更关注的是微弱扰动对于模型性能的影响,所以扰动的能量大小和对抗样本的SSIM显得非常重要.
1)ReID攻击通常会设定攻击的能量上限,借鉴对抗机器学习(Adversarial Machine Learning, AML)中关于对抗攻击能量大小的度量方法[16],给定图像宽度W、高度H,设定能量大小度量指标为
其中I为图像像素总数.
2)为了度量对抗样本和原始图像的结构相似性,给定图像的SSIM指标如下:
SSIM(I,I′)=[l(I,I′)α·c(I,I′)β·s(I,I′)γ].
上式基于I和I′之间的亮度、对比度和结构进行综合衡量:
其中,α=1,β=1,γ=1,可得
其中:μ、μ′分别表示I和I′的平均值;σ、σ′分别表示I和I′的方差;ρ表示I和I′的协方差;c1=(k1L)2,c2=(k2L)2,用于持续稳定的常数,一般取c3=c2/2;L表示像素值的动态范围;k1=0.01,k2=0.03.
SSIM值越大说明对抗样本与原始图像的相似度越高.SSIM可较好地度量对抗样本和原始图像之间的相似度,是衡量对抗样本质量的重要指标.在本文实验中,采用高斯函数计算图像均值、方差及协方差,而不是遍历像素点的方式.
2.4 攻击实验结果
现有的ReID模型主要分为基于变形器网络Transformer的模型和基于CNN的模型,下面分别使用MSG-AEGN对2种代表性模型进行攻击实验.
2.4.1对Transformer框架ReID模型的攻击
本文攻击目前性能最优的ReID模型——TransReID(Transformer ReID)[12],该模型以Transformer[31]为框架基础.由于TransReID分别使用不同的方法训练它的骨干网络Vision Trans-former(ViT),本文在实验中也相应使用MSG-AEGN攻击基于这些方法训练的ViT骨干网络.攻击前后性能对比如表2所示,表中基准算法-ViT表示不使用JPM(Jigsaw Patch Module)和SIE(Side Informa-tion Embeddings)[12]训练的ViT骨干网[12],Trans-ReID-ViT表示使用JPM+SIE训练的ViT骨干网,TransReID-DeiT表示以DeiT(Data-Efficient Image Transformers)[32]预训练模型训练的ViT骨干网.
由表2可知,MSG-AEGN攻击TransReID,可使其mAP值降至2.5%以下,并保持对抗噪声的L1范数能量低于30,对抗样本与原始图像的SSIM值高于70%.值得注意的是,不同的训练方法对同个骨干网络结构进行训练,获得模型的鲁棒性(防御对抗攻击的能力)是不同的.

表2 MSG-AEGN攻击TransReID前后性能对比Table 2 Performance comparison before and after MSG-AEGN attacking TransReID
2.4.2对CNN框架ReID模型的攻击
为了和更多的ReID攻击算法对比,实验选择TCIAA和MUAP作为对比算法.对扰动能量上限进行限定,在Market1501数据集上,MUAP和TCIAA的扰动样本能量上限均为16;在DukeMTMC-reID数据集上,MUAP和TCIAA的扰动样本能量上限分别为11和16.为了全面对比分析,本文利用MSG-AEGN、TCIAA、MUAP分别对目前主流的基于CNN的ReID模型进行攻击,包括AlignedReID[32]、AGW(Non-local-Attention Generalized-Mean Weighted-Regularization-triplet)[33]、BOT(Bag of tricks)[34]及其在3种不同骨干网络ResNet50、DenseNet121和SENet154上的变种.攻击实验在Market1501、Duke-MTMC数据集上进行,结果如表3和表4所示.
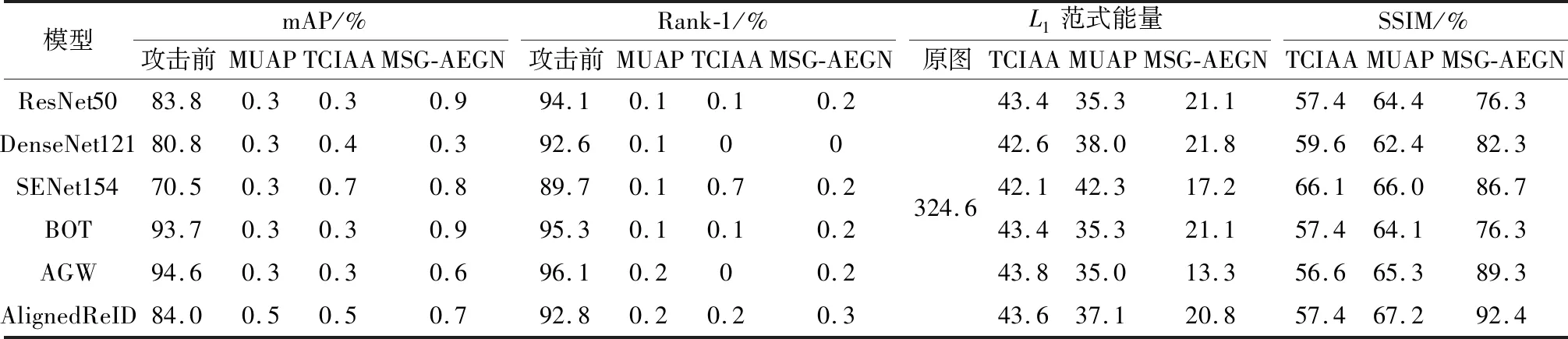
表3 3种模型在Market1501数据集上攻击基于CNN的基准ReID前后性能对比Table 3 Performance comparison before and after 3 models attacking ReID baselines based on CNN on Market1501 dataset
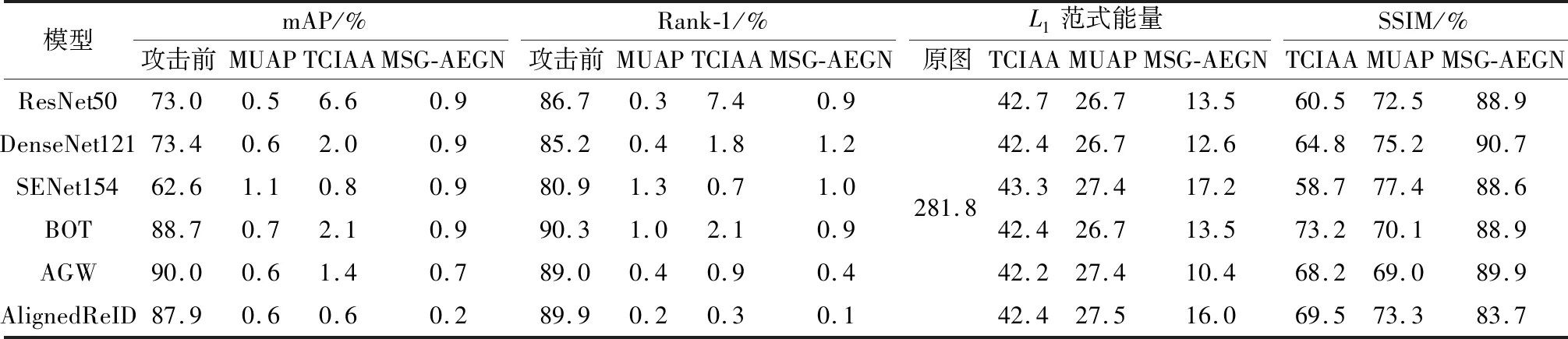
表4 3种模型在DukeMTMC-reID数据集上攻击基于CNN的基准ReID前后性能对比Table 4 Performance comparison before and after 3 models attacking ReID baselines based on CNN on DukeMTMC-reID dataset
由表3可看出,在 Market1501 数据集上,MSG-AEGN在攻击AlignedReID时,相比TCIAA和MUAP,攻击所需能量值分别降低22.8和16.3,SSIM值分别提升35.0%和25.3%.由表4可知,在DukeMTMC-reID数据集上,MSG-AEGN在攻击AGW时,相比TCIAA和MUAP,扰动能量分别降低31.8和17.0, SSIM分别提升21.7%和20.8%.实验表明,MSG-AEGN不但能提升视觉质量(SSIM),还能大幅抑制能量大小.
在不同数据集上,使用MSG-AEGN、TCIAA和MUAP攻击不同的目标ReID模型(DenseNet、AGW、BOT),生成的对抗样本可视化结果如图6所示.

(a)MSG-AEGN的攻击结果(a)Results by MSG-AEGN
2.5 单尺度网络与多尺度网络攻击效果对比
在Market1501、DukeMTMC-reID数据集上,基于MSG-AEGN验证多尺度网络对抗样本能量抑制性能强于单尺度网络.在DukeMTMC-reID数据集上设计MSG-AEGN攻击BOT和AGW,前后性能对比如表5和表6所示.
由表5可见,MSG-AEGN攻击BOT,在遭受对抗攻击后,无论是单尺度攻击或多尺度攻击都能使BOT的mAP值从88.7%降至0.9%,Rank1值从90.3%降至0.9%,但是单尺度攻击对抗扰动能量大于多尺度攻击.

表5 各网络在Market1501数据集上攻击ReID模型前后性能对比Table 5 Performance comparison before and after different networks attacking ReID models on Market1501 dataset
同理,由表6可见,在DukeMTMC-reID数据集上的结果也同样表明多尺度攻击需要的对抗扰动攻击能量更低,能大幅抑制攻击能量.

表6 各网络在DukeMTMC-reID数据集上攻击ReID模型前后性能对比Table 6 Performance comparison before and after different networks attacking ReID models on DukeMTMC-reID dataset
单尺度网络攻击和多尺度网络攻击部分可视化结果如图7所示.

(a)攻击BOT(a)Attacking BOT
由图7可见,在DukeMTMC-reID数据集上,以MSG-AEGN对BOT的攻击为例,从可视化样本中可发现,以红色限定区域为参考进行对比,多尺度网络攻击由于获得原始样本像素修改的深层权重,在浅层对像素的修改幅度明显弱于单尺度网络攻击,对抗扰动的能量也相对较低.总之,相比多尺度网络,单尺度网络生成的对抗样本能量增加,SSIM值减小.
下面通过实验验证4×2分辨率层对于实验结果的影响.在Market1501数据集上,目标网络为AGW,使用MSG-AEGN攻击AGW,在所用参数不变的情况下,去除4×2分辨率层前后可视化结果对比如图8所示.

图8 去除4×2层前后生成的对抗样本可视化结果Fig.8 Visualization results before and after removing 4×2 layer
在使目标模型的mAP和Rank1都低于1的攻击强度之下,保持4×2分辨率层产生扰动样本的L1范式能量为13.1,SSIM值为89.4%;去除4×2分辨率层后,产生扰动样本的L1范式能量为18.8,SSIM值为81.8%.由此可知,去除4×2分辨率层会增加对抗扰动的能量大小,降低对抗样本与原始样本的SSIM值.由图8还可看出,去除4×2分辨率层后对抗扰动痕迹更明显,肉眼观察下更容易被察觉.
2.6 对抗损失函数与改进型对抗损失函数性能对比
为了验证改进型对抗损失函数在其它模型上的效果,本文以TCIAA攻击方法为例,在Market1501数据集上对AlignedReID目标模型进行攻击.在1 min 45 s内,使用对抗损失函数的TCIAA和使用改进型对抗损失的TCIAA均完成10个批次的训练.此时,使用对抗损失函数的TCIAA在测试集上的mAP值由79.1%降至59.2%,Rank1值由91.8%降至73.8%.在其它实验设置和网络结构不变的情况下,将对抗损失函数替换成改进型对抗损失之后,TCIAA在测试集上的mAP值由79.1%降至13.5%,Rank1值由91.8%降至15.7%.由此可见,相比对抗损失函数,利用改进型对抗损失函数进行模型训练,在相同训练时间条件下获得的模型泛化性能具有明显提升.
为了进一步验证改进型对抗损失的有效性和适用性,将MSG-AEGN中的改进型对抗损失替换为TCIAA的对抗损失函数.以对AlignedReID目标模型的攻击为例,在Market1501数据集上,目标模型被MSG-AEGN使用对抗损失函数攻击之后,mAP值由79.1%小幅降至78.2%,Rank1值由91.8%降至90.6%,几乎没有攻击效果.在其它实验设置和网络结构不变的情况下,将对抗损失函数替换成改进型对抗损失,mAP值由79.1%降至4.4%,Rank1值由91.8%降至3.7%.由此可见,使用TCIAA攻击模型的损失函数对MSG-AEGN的训练没有效果.
综上所述,在TCIAA中改进型对抗损失函数的性能明显强于对抗损失函数,在MSG-AEGN中对抗损失函数几乎没有作用,而改进型对抗损失函数的攻击效果较明显.由此可证实,改进型对抗损失函数的可迁移性强于对抗损失函数.
2.7 消融实验结果
为了验证本文的改进型对抗损失函数和能量抑制函数的有效性,进行多组消融实验.
在CUHK03数据集上,MSG-AEGN分别攻击AlignedReID、DenseNet121,攻击前后性能对比如表7所示.以攻击AlignedReID为例,不使用改进型对抗损失时,mAP值仅从59.7%降至57.8%,Rank1值仅从60.9%降至59.1%,无太大变化,攻击效果不明显.反之,使用改进型对抗损失时,mAP值从59.7%降至1%,Rank1值从60.9%降至0.6%.由此可见,改进型对抗损失函数对MSG-AEGN攻击性能的影响较明显.
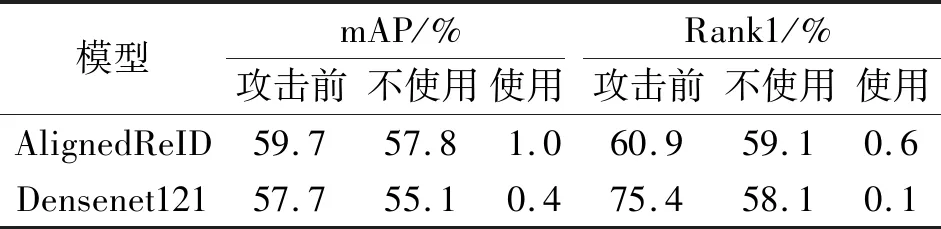
表7 改进型对抗损失函数对MSE-AEGN性能的影响Table 7 Effect of improved adversarial loss function on MSE-AEGN performance
为了验证能量抑制函数Lp的有效性,是否使用能量抑制损失函数的性能对比如表8所示.由表可见,使用能量抑制函数得到的对抗扰动能量远低于不使用能量抑制函数,因此可得,能量抑制损失函数在不同数据集和骨干网络上可有效抑制生成对抗扰动样本的能量大小.
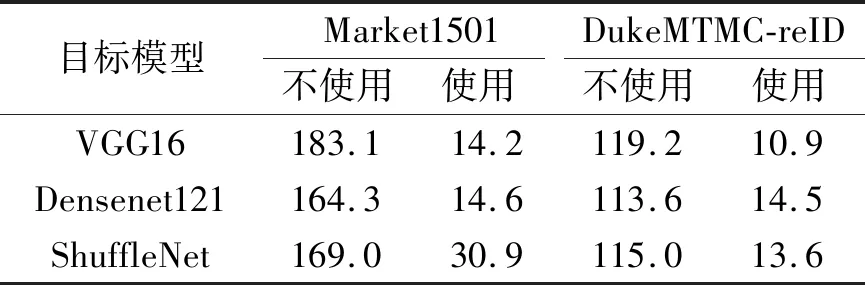
表8 能量抑制函数使用前后L1范式能量对比Table 8 Energy comparison of L1 normal form before and after energy suppression function
3 结 束 语
本文设计基于多尺度梯度对抗样本生成网络(MSG-AEGN),通过多尺度结构在不同分辨率上调制原始样本像素,从而获得扰动能量较低、视觉质量较高的对抗样本.实验表明,MSG-AEGN对基于CNN和Transformer的主流Re-ID模型均具有较好的攻击效果.尽管现有的行人重识别对抗攻击模型通过不断改进以提升对抗样本视觉质量,但离生成肉眼完全无法识别的对抗扰动这一目标还有一定差距,亟待解决诸多问题.今后可考虑生成能量更低、肉眼更难以察觉的对抗扰动,并探索其它攻击模式的对抗攻击方法,力争实现攻击效果的新突破.

