永磁直驱风力发电机定子绕组电压分布仿真计算与测试

何明鹏，张 跃，刘学忠，范琦睿，胡 波，梁智明，袁鹏飞，刘 枰

（1.东方电气集团东方电机有限公司，四川 德阳 618000；2.西安交通大学 电力设备电气绝缘国家重点实验室，陕西 西安 710000）

0 引言

随着电力电子行业的不断发展，快速开关器件（如IGBT）和逆变器（或变流器）被广泛应用于交流旋转电机的调速。然而一系列相关研究[1-3]表明，变频器侧产生的高频重复激励脉冲施加在电机定子（或转子）绕组上时会对其绝缘系统造成过早击穿，甚至影响电机的正常运行。

脉宽调制（pulse width modulation,PWM）逆变器的高频重复激励脉冲对于电机绕组绝缘的影响主要体现在两个方面：一方面是由于连接电缆与电机绕组间的阻抗不匹配，当脉冲上升（或下降）沿到来时电机绕组会产生较高幅值的重复过电压，相关研究发现电机绕组过电压的幅值与连接电缆的长度以及分布参数密切相关[4-5]；另一方面是三相PWM激励脉冲也会导致沿电机绕组上的电压分布极度不均，特别是最靠近电机接线端子的首组线圈内部的匝间电压，从而加速绕组绝缘系统老化甚至引发过早击穿，这一现象可以由多导体传输线理论来进行计算和解释[6-8]。目前对于变频电机绕组电压分布的仿真研究主要是将绕组线圈视为一条均匀的传输线路，从而忽略了位于铁芯部分的线圈与位于电机端部的线圈之间分布参数的不同[9-10]。实际上，由于集肤效应以及邻近效应的影响，位于铁心内部的线圈等效电阻与等效电感参数会随着输入脉冲方波的上升沿等效频率变化而变化，忽略频率作用而计算的分布参数并不准确。此外，由于逆变器三相PWM激励脉冲的复杂特性，少有相关的仿真研究是建立在完整的三相绕组模型基础之上的。为简化分析过程，多数研究仅在单相绕组等效电路的一段输入脉冲方波，而另一端直接接地[11-13]。然而在实际运行过程中，Y型连接的三相绕组中性点并不是直接接地，且中性点的电位受到另外两相绕组输入的影响。文献[14-15]研究表明，通过仿真计算结合实验的方法分析三相PWM脉冲作用下电机绕组的电压分布以及过电压幅值特性，能够为变频电机绕组绝缘系统的设计提出合理有效的方案。

本研究以永磁直驱风力发电机为例，基于PSCAD/EMTDC软件建立三相定子绕组等效电路模型，通过有限元计算方法得到等效电路的分布参数，应用暂态仿真计算结合实验平台验证的方法，分析三相PWM激励脉冲下定子绕组对地、线圈间以及匝间的电压波形及峰值的分布特性。

1 仿真计算及实验测试平台

1.1 定子绕组等效电路模型

为了准确分析电机定子绕组的重复脉冲电压分布特性，本研究建立了额定电压为0.69 kV、容量为2.5 MW的永磁直驱风力发电机组的三相定子绕组等效电路模型。三相定子绕组连接方式为星形连接，每相绕组由8组（只）线圈串联构成，每组线圈包含12匝导体。建立的风力发电机完整三相定子等效电路仿真模型如图1所示，变频器产生的PWM脉冲通过连接电缆施加于三相定子绕组，由于三相定子绕组的结构和参数一致，仿真时将仅以一相（如U相）定子绕组为例，分析其电压波形及其分布特性。

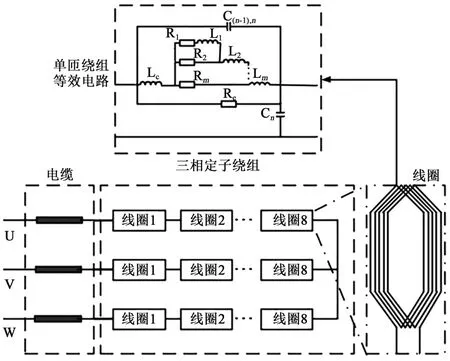
图1 完整仿真等效电路模型Fig.1 Complete equivalent circuit model for numerical simulation

图1所示的单匝绕组等效电路模型中，C(n-1),n和Cn分别表示匝间以及匝对地的等效电容，Re为线圈铁心内部涡流损耗的等效电阻，Lc为各匝导体端部的等效电感。考虑到铁心内部的集肤效应和邻近效应，各匝导体的等效电阻及电感可以由阶梯型RL电路组成[16]。针对不同频率等级的输入脉冲，RL阶梯电路体现不同的阻抗特性。当输入脉冲等效频率较高时，等效电路的上级台阶起主导作用；而对于较低等效频率的脉冲，主要由电路的下级台阶决定其等效阻抗。其中，Rm和Lm分别代表各阶频率对应的等效电阻和等效电感，参数m表示阶数。在此次仿真过程中，输入脉冲的频率范围为0.01～10 MHz，因此，阶数m的值可以选取为1～4，分别对应频率0.01、0.1、1、10 MHz。

等效电路模型的分布参数可以通过多物理场有限元分析软件COMSOL进行计算。图2所示为建立的单匝线圈二维截面模型，输入对应电机绕组的尺寸和材料参数即可在静电场下计算得到单匝线圈的对地电容、匝间电容、端部等效电感以及涡流损耗等效电阻。此外，在频域使用参数化扫描即可得到不同频率下RL阶梯电路内的等效电感以及等效电阻。该风力发电机定子绕组分布参数值如表1所示。

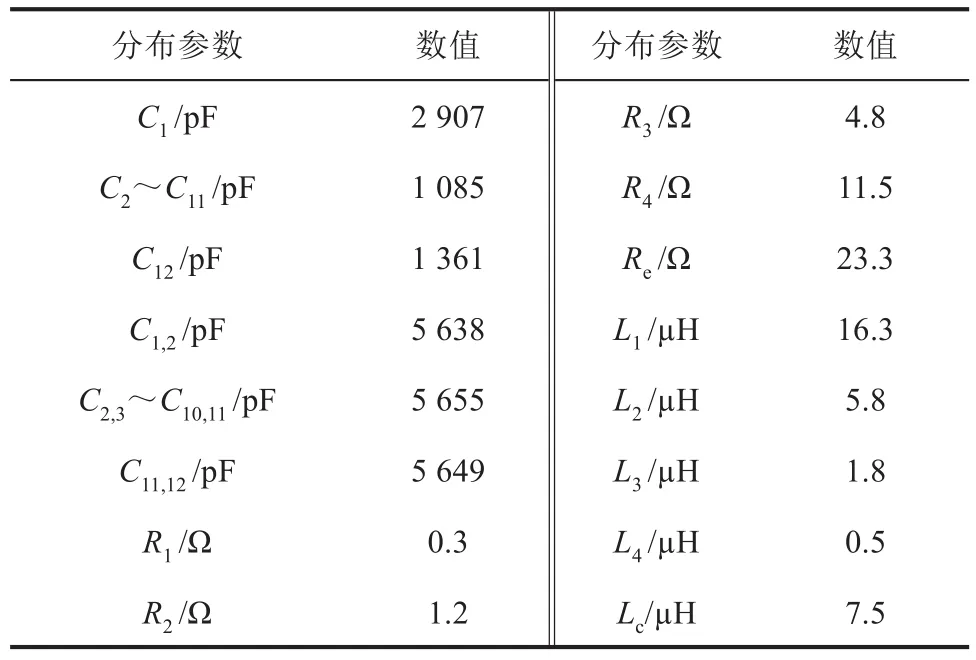
表1 定子绕组模型分布参数值Tab.1 Distributed parameters of stator winding

图2 单匝线圈二维截面模型Fig.2 Two-dimensional cross section of single turn coil

1.2 实验测试平台

为验证仿真结果的准确性，同时获取连接电缆及定子绕组情况下变频器机侧的实际输入脉冲波形，需要搭建与仿真系统对应的实验测试平台。实验测试平台的整体结构及组成如图3所示，整个测试平台基于一台容量为2.5 MW的永磁直驱风力发电机组建立，实验过程中将发电机的永磁转子拆除，仅保留定子部分，经由长度约为100 m的电缆连接PWM逆变器。为方便测量，实验前除去绕组线圈上的主绝缘，使得发电机定子绕组U相的一条支路中各组线圈的首匝导体裸露并作为线圈对地以及线圈间电压信号的测量点；此外将靠近电机端子的首组线圈鼻部绝缘结构拆除，使得该线圈的各匝导体裸露作为匝间电压信号的测量点。测量过程中，将各个线圈按照由端子到中性点的顺序依次编号为1，2，…，8。测量使用的高压探头型号为P6015A，带宽为75 MHz。实验过程中门极电压设定为1.12 kV，载波频率为3 kHz，基波频率为35.7 Hz。

图3 实验测试平台示意图Fig.3 Schematic diagram of experiment platform

2 结果与讨论

2.1 线圈对地电压分布特性

为分析电机U相定子绕组的电压分布特性，同时保证仿真与实验对比的有效性，将实验测试平台测得的变频器所产生的PWM高频脉冲作为仿真输入施加于三相定子绕组等效模型，分别通过仿真和测量得到线圈（匝）对地、线圈间以及第一线圈各匝间的电压波形，并进行对比和分析。由实验测试平台测试获得的PWM逆变器输出相间电压脉冲波形如图4所示。从图4可以看出，在脉冲的上升（或下降）处，变频器机侧输出的高频重复脉冲会产生过冲电压，其幅值最高可达1.25 kV，比门极电压1.12 kV高了约12%，脉冲的上升时间为0.6 μs。

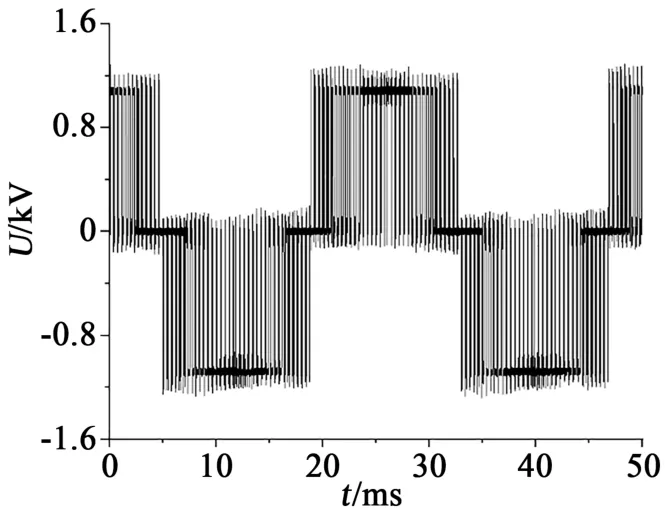
图4 PWM变频器产生的激励脉冲Fig.4 Excitation impulse generated by PWM converter

定子绕组内线圈1对地电压波形的实测及仿真结果如图5所示。从图5可以看出，在脉冲上升（或下降）处，各线圈对地电压均经历短暂过冲后趋于稳定。这是由于在激励脉冲产生的瞬间，定子绕组的初始电压分布由各组线圈的杂散电容决定。随后绕组中的电压波与电流波受绕组的杂散电容和电感等分布参数的影响，在传播过程中发生短暂的震荡。而在震荡结束后，绕组内部稳态电压将根据电阻均匀分布。实测与仿真电压波形较为吻合，其稳态值基本一致，而实验测得的过电压幅值（1.2～1.3 kV）略高于仿真结果（1.1～1.2 kV）。

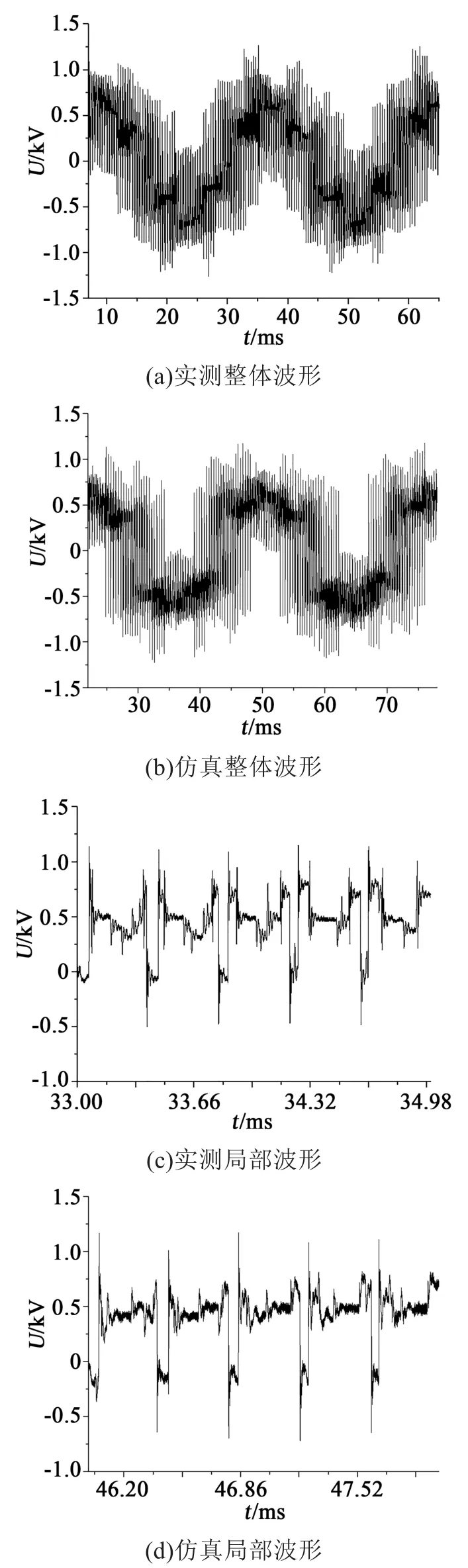
图5 首组线圈对地电压波形Fig.5 Waveform of voltage for the first coil to ground

统计仿真和实验过程中各组线圈对地电压波形中重复出现的过电压峰值，其结果如图6所示。图6中N表示每相绕组从端子开始的线圈序号，Up表示电压峰值。仿真得到的U相绕组各线圈对地电压峰值分布与实验测量结果基本一致，实测电压峰值略大于仿真值。从整体上看，线圈对地电压峰值沿电机端子到绕组中性点有明显减小的趋势。靠近端子的前两组线圈承担着较高的对地电压，而后几组线圈的对地电压分布相对均匀。最大对地电压出现于第1组线圈，其实测值和仿真值分别为1.29 kV和1.19 kV，二者误差在8%以内。

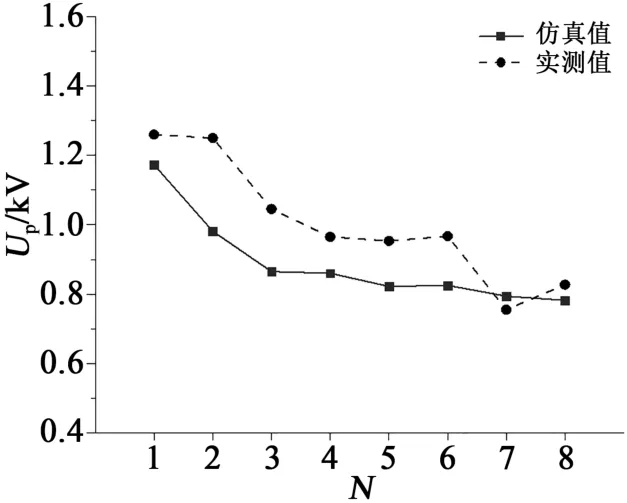
图6 各线圈对地电压峰值Fig.6 Repetitive coil-to-ground peak voltage

2.2 线圈间电压分布特性

将U相绕组中各个相邻线圈首端对应的对地电压波形相减，即可得到U相绕组各组线圈间的电压，其中第1组线圈与第2组线圈间（即第1组线圈的首末间）电压波形的实测与仿真结果如图7所示。从图7可以看出，实测波形与仿真波形均在脉冲上升（或下降）瞬间有明显电压过冲现象发生。然而相比于实验测量得到的电压波形，仿真计算结果中第1与第2组线圈间过电压的震荡时间较长且最大幅值（1.2～1.3 kV）略高于实测结果（0.8～1.1 kV）。

图7 第1与第2组线圈间电压波形Fig.7 Waveform of voltage between first and second coils

一相绕组各线圈首末间的电压峰值统计结果如图8所示。从图8可以看出，仿真得到的线圈间电压峰值分布与实验结果较为一致，实验测量的电压峰值略低于仿真结果。线圈间的电压峰值沿电机端子到中性点依旧呈现明显减小的趋势，且最大电压峰值发生在第1与第2组线圈间，对应的实测与仿真值分别为1.05 kV和1.22 kV。由此可以推测，最大匝间电压可能发生在第1组线圈上，即最靠近电机端子的线圈内部。

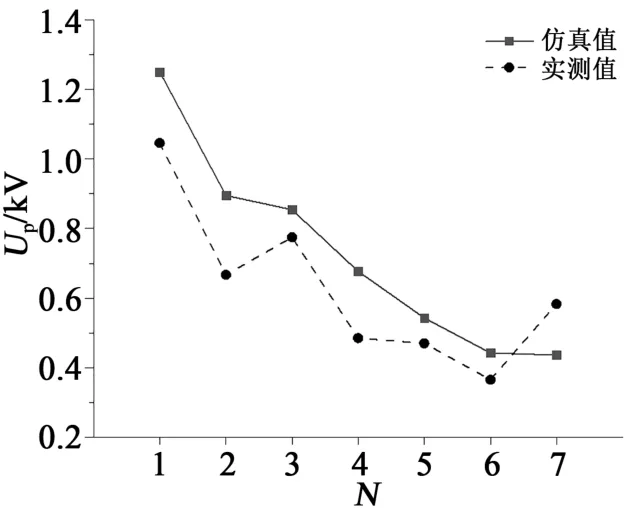
图8 线圈间电压峰值Fig.8 Repetitive coil-to-coil peak voltage

2.3 线圈内匝间电压分布特性

由2.2结果可知，以首组线圈为例分析单组线圈内各匝导体间的电压分布更具有典型性。首组线圈内第1匝与第2匝导体间电压的实测以及仿真波形如图9所示。从图9可以看出，实验测量与仿真计算波形的过电压幅值及稳态值分布趋势基本一致，相比于实测的电压波形中较为短暂的震荡过程，仿真的电压波形震幅更高。

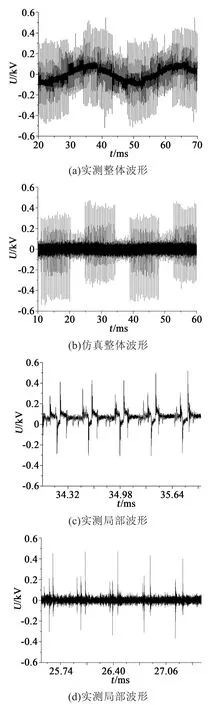
图9 首组线圈内第1与第2匝间电压波形Fig.9 Waveform of voltage between first and second turns in first coil

图10是首组线圈内匝间电压峰值。从图10可以看出，单组线圈内部从首匝到末匝导体间的电压峰值逐渐减小。最大峰值电压出现在第1匝与第2匝导体之间，且明显高于绕组的其他匝间电压，其仿真计算的最大峰值为0.57 kV。在实验测量中，绕组前4匝的匝间电压峰值与仿真结果基本吻合，而绕组的后续匝间电压峰值呈现波动分布。

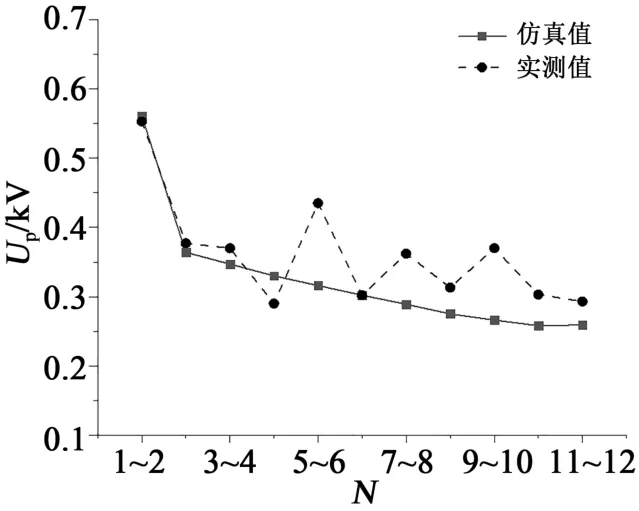
图10 首组线圈内匝间电压峰值Fig.10 Repetitive turn-to-turn peak voltage in first coil

3 结论

（1）沿永磁直驱风力发电机各相绕组从端子到中性点分布的线圈匝对地以及线圈间电压峰值均呈现明显减小的趋势，这意味着定子绕组中首组线圈的主绝缘承受着较高的电压，相对应地应当提高该部分绝缘强度。

（2）在最靠近电机接线端子的首组线圈内，第1匝与第2匝绕组之间的匝间电压峰值明显大于后续绕组，因此应适当提高第1、2匝间的匝间绝缘强度。

（3）实验测试结果与仿真计算结果较为一致，验证了该三相全定子绕组仿真模型的准确性和有效性。