北方干旱半干旱区洪水极值事件多变量频率分析

曹 丹

(辽宁省葫芦岛水文局，辽宁 葫芦岛 125000)

在水文分析计算中，常常根据某一类极值事件，例如洪水、暴雨，单变量，对该极值事件中包含的某一种特征属性，如洪峰、洪量、洪水持续时间进行频率分析以得到该类极值事件下某一频率对应的设计值[1]。然而在实际中，一种属性往往无法准确地描述该类极值事件的具体特征，也无法构建该类极值事件的某一特征和其他事件的某一属性值之间的相互关系。一些特征变量之间的联合分布无法采用单变量频率分析方法进行全面描述，变量之间的相关结果也无法刻画。因此，要解决此项问题需要通过多变量水文频率分析的方式进行[2]。Copula函数是近年来常用于多变量频率分析的一种方法[3- 12]，与其他多变量频率分析方法相比，Copula函数对于边缘独立分布的随机变量进行相关性结构的反映，分为2个独立的部分来对变量联合分布进行计算，从而构建多个相关结构的变量边缘分布概率函数，通过函数变化形成多个变量之间的联合分布，由于在边缘分布函数里对变量所有特征进行包含，因此在函数变换过程中信息不会有所损失。通过Copula函数可以构建洪峰流量、洪水历时、洪量之间的联合分布来全面地描述洪水，也可以将洪水事件与降水事件结合，通过考虑气象要素与洪水特征之间的相互关系，进而分析气象要素对洪水极值事件的影响[13]。从而对某一区域的洪水频率分析提供更全面、更科学的设计值[14]。辽西地区近些年来受气候变化影响，洪水极值发生不同程度的变化，亟需对其洪水极值和降雨条件联合分布概率进行探讨，从而为应对气候变化影响的区域洪水影响制定相对应的科学措施。为此本文选取东白城子以上流域为研究实例，结合区域实测洪水和降水数据，基于二维Copula函数建立洪水极值和降水的联合分布概率，从而确定区域洪水极值在不同降水条件下的合概率分布。

1 研究方法

Copula函数的种类较多，其中Gumbel-Hougaard Copula函数的上尾和下尾相关系数适合对水文变量进行描述，其函数主要原理由于参考文献较多，本文就不做过多介绍，分别采用Pearson相关系数等5种方法对其变量间的相依性度进行计算，Copula函数概率分析时候需要设{(x1，y1)，(x2，y2)，……(xn，yn)}为分析变量x、y的连续观测样本，则各相关系数的计算方程分别为：

(1)

(2)

(3)

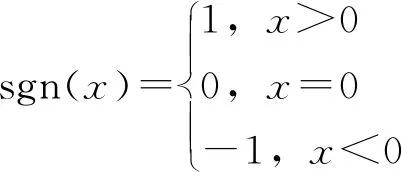
(4)

除上述3种相关系数外，Chi图和K图也是常见的用于描述变量间相依性的方法，Chi图的计算原理如下：

(5)

(6)

(7)

则有：

(8)

(9)

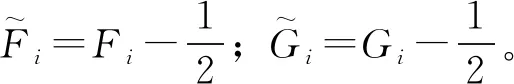
(10)

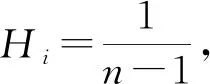
(11)

式中，

(12)

2个变量X、Y在K图中具有一定的相依度，Win和K0(ω)关系曲线均会对(Win，H(i))的所有数据在带状区域内进行圈围，2个变量之间的越高的相依度则其关系曲线越为接近。

2 研究区域概况

东白城子水文站以上流域位于绕阳河流域内，绕阳河源出阜新蒙古族自治县扎兰营子乡察哈尔山，于盘山县东郭镇万金滩注入辽河，河流总长度326km，流域面积10438.20km2，其中干流河段河道长度48.19km。流域内山丘漫岗区占总面积的43.30%，冲积平原区占56.70%，平均坡降1.72%。流域降水量和蒸发量多年均值分别为485、1750mm，降雨受季风气候影响时空分布差异较大，从南到北降水逐步递减，降水主要集集中在汛期，占全年降水量的比重超过80%。低山丘陵是绕阳河流域的主要地形，土壤产水能力较低，暴雨洪水主要集中在汛期。绕阳河干流自河源以下共有4个水文站，分别是韩家杖子站、东白城子站、四家子站和杜家站。东白城子水文站以上流域为绕阳河上游，集水面积2070km2。东白城子流域内共有10个配套雨量站。

3 分析结果

3.1 变量序列样本选取

选取的水文站点为东白城子流域出流站东白城子站。基于东白城子水文函及流域内10个雨量站时间序列的交集，选取的时间序列范围为1967—2018年。采用年最大值法(AM)选取东白城子站年最大洪峰序列作为洪水极值事件的洪峰序列，在降水样本选取时，充分考虑降水和洪水之间的相关性以及两者在物理成因上的相互而选取最具代表性的降水序列。基于此，本节选用前期累计面降水量序列作为降水序列。采用泰森多边形法，基于东白城子流域10个雨量站点的点降水量资料，计算东白城子流域的面降水量序列。随后，从最大洪峰发生的时间开始，从当天往前推算Nd的累积降水量，通过计算不同前推时间N下，累积降水量序列和年最大洪峰序列之间的相关系数，选取相关系数对应的Nd累积降水量序列进行下一部分的工作。前期累积降水量(N=1，2，……)和年最大洪峰流量序列之间的相关系数如图1所示。

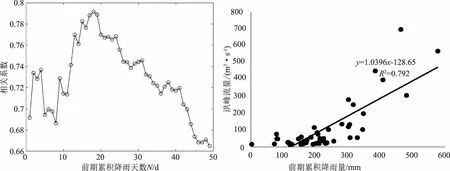
图1 前期累积面雨量序列与年最大洪峰序列的相关性

可以清晰看出，当N=18d时，前期累积降水量与年最大洪峰序列之间的相关性最高，其对应的相关系数为0.792。N=18d对应的相关性如图1所示。为此最大洪峰年序列和降水量前期累积量对应的N值为18d，2个变量之间的相应性结构采用Copula函数进行描述。

3.2 多变量边缘分布的确定

采用极大似然法估计确定东白城子站1960—2018年年最大洪峰流量序列、年最大洪量序列、年最长洪水历时序列10种频率分布下的参数，并采用拟合度比较方法确定各个序列的最优分布。东白城子站、韩家杖子站各分布的经验频率与理论频率的拟合度及最优分布选择结果见表1。

表1 东白城子站洪峰、洪量、历时最优分布选择

从计算结果中可以看出，在东白城子站，1960—2018年年最大洪峰序列、年最大洪量序列、年最长洪水历时序列的最优分布分别是P-Ⅲ型分布、GPD分布。基于此，选择各变量对应的最优分布作为构建Copula函数的边缘分布。

3.3 序列的相依性度量计算

年最大洪峰和洪量序列的分析年份为1960—2018年，分别对洪峰和洪量、洪峰与历时以及洪量与历时的Pearson相关系数γ，Spearman相关系数ρ和Kendall相关系数τ进行两两序列计算，结果见表2。对于相依性较好的洪峰与洪量序列，可以采用Copula函数描述两者之间的相依性结构，对于相关关系不好的序列，不建议采用Copula函数进行分析。为此还采用Chi图、K图进一步验证东白城子站年最大洪峰流量、年最大洪量之间的相关性，如图2所示。

表2 东白城子站两变量间的相依性度量

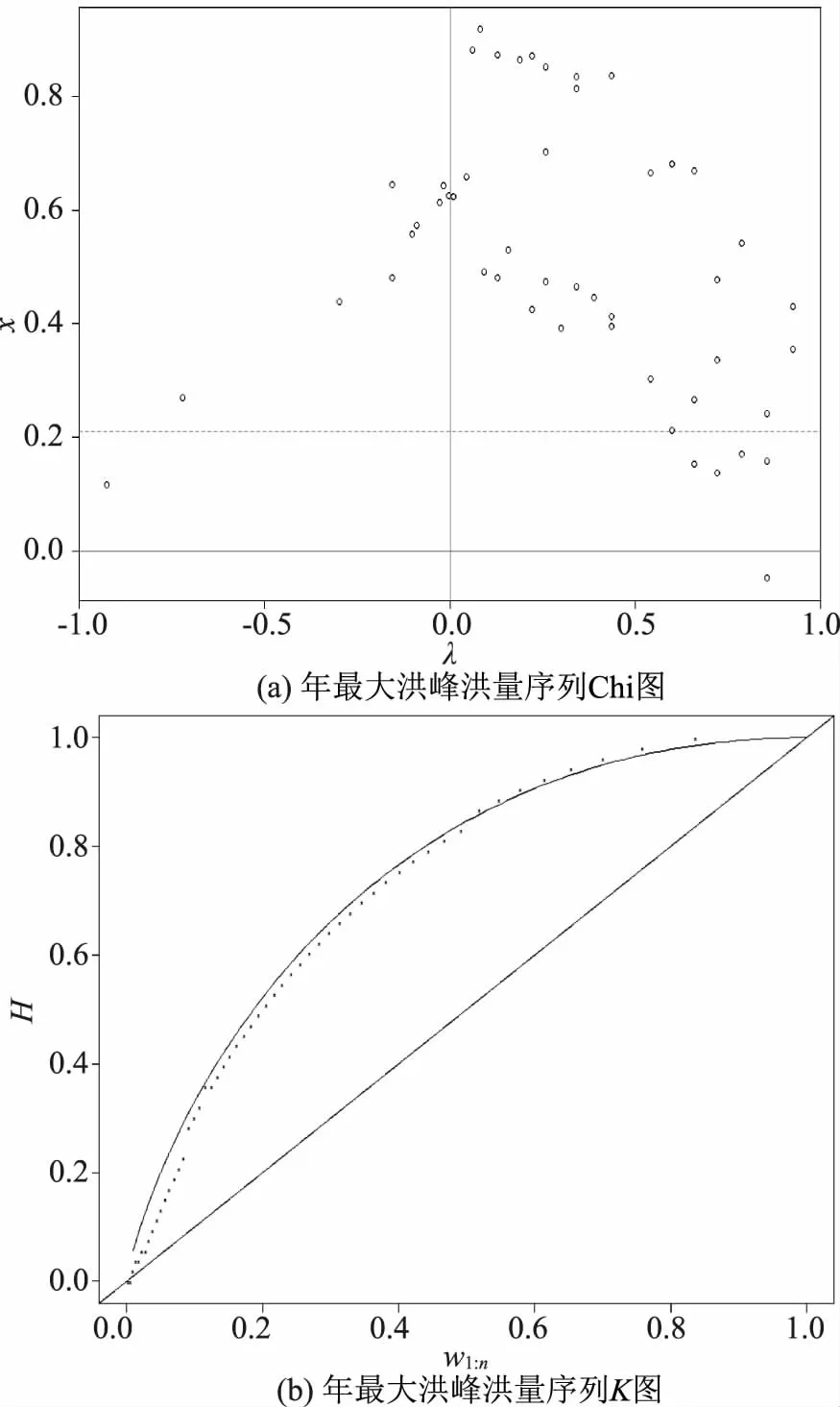
图2 东白城子站年最大洪峰洪量序列Chi和k图

从计算结果中可以看出，对于东白城子站，洪峰、洪量之间的相依性较好，不论是Pearson相关系数γ，Spearman相关系数ρ和Kendall相关系数τ均达到了0.6以上，而洪峰与洪水历时，洪量与洪水历时之间的相依性并不好，不论是Pearson相关系数γ，Spearman相关系数ρ和Kendall相关系数τ，均没有超过0.2。从图2中也可以看出，东白城子站年最大洪峰序列与年最大洪量序列之间具有良好的相依性，在其Chi图中，除个别点外，其余所有点据均落在虚线置信区间外。而在K图中，除个别点据外，Win和K0(ω)的关系曲线和对角线所围区域内均包含剩余点据，关系曲线和点据具有较好的拟合度，由此说明东白城子站年最大洪峰序列与年最大洪量序列之间具有较强的相依性。此外，从Chi图中还可以发现，除了一个点外，所有的点的χi均大于0，由此也进一步说明了东白城子站的年最大洪峰序列与年最大洪量序列之间存在正象限相关关系。

3.4 拟合度检验结果

分别采用Gumbel Copula，Clayton Copula，Frank Copula 3种Copula函数，建立东白城子站年最大洪峰、洪量序列之间的联合分布函数，分别采用2种方法对不同Copula函数进行参数估计，最后进行拟合优度检验并选择拟合效果最优的Copula函数。根据RMSE的计算公式，RMSE值越小代表拟合优度越高，以此为标准选择最优的Copula函数及最优的参数估计方法。东白城子站年最大洪峰洪量序列Copula参数计算结果见表3。

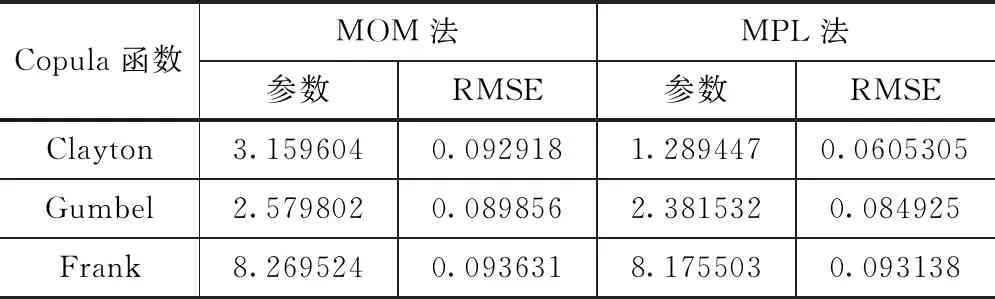
表3 东白城子站年最大洪峰洪量序列的Copula函数参数估计及拟合优度检验

从上表中可以看出，采用矩估计法(MOM法)对东白城子站年最大洪峰序列与年最大洪量序列之间不同Copula函数进行参数估计时，拟合效果最佳的为Gumbel Copula函数，拟合效果相对较差的是Frank Copula函数和Clayton Copula函数。在该站采用伪极大似然法(MPL法)估计参数时，采用Clayton Copula函数的拟合效果最好，Frank Copula函数拟合效果最低，Gumbel Copula函数拟合效果好于Frank Copula函数，因此在东白城子站采用MPL方法得到的Copula函数的拟合效果均更佳。此外，在东白城子站，通过MPL方法估计Clayton Copula函数参数得到的拟合效果最佳，由此说明Clayton Copula函数为东白城子站年最大洪峰、洪量序列的最优拟合分布。因此选用Clayton Copula函数，用于构建东白城子站年最大洪峰序列、年最大洪量序列之间的联合分布函数，且参数估计方法均选用MPL方法。

3.5 多变量模型分析

基于东白城子站、韩家杖子站的年最大洪峰、洪量之间的最优Copula函数，绘制了相应的联合重现期等值线图(重现期分别为5、10、20、50、100年)，其结果如图3所示。

图3 东白城子站洪峰洪量两变量联合重现期

年最大洪量/洪峰流量无论何种重现期，随着年最大洪峰流量/洪量的增加其发生的条件概率呈现递增变化，即说明东白城子站年最大洪峰与年最大洪量之间呈现明显的正相关关系，在洪峰流量较大的情况下，发生较大洪量洪水的可能性也较大，这也与实际事实相符合。此外，从上图中也可以看出，在同一洪峰流量/洪量下，重现期较小的情况下对应的洪量/洪峰流量发生的累积概率要明显大于重现期较大情况下对应的洪量/洪峰流量发生的累积概率，这一点与实际情况也是相符的，因为在相同的洪峰流量/洪量条件下，重现期小的洪水比重现期大的洪水更易发生。

4 结论

(1)采用矩估计法(MOM法)估计北方干旱半干旱区域年最大洪峰序列与年最大洪量序列之间不同Copula函数的参数时，拟合效果最好的是Gumbel Copula函数，拟合效果相对较差的是Clayton Copula函数和Frank Copula函数。

(2)对于北方干旱半干旱区而言，洪峰、洪量之间的相依性较好，Pearson相关系数γ、Spearman相关系数ρ和Kendall相关系数τ均达到了0.6以上，而洪峰与洪水历时，洪量与洪水历时之间的相依性较低，Pearson相关系数γ、Spearman相关系数ρ和Kendall相关系数τ均低于0.2。

(3)本文在变量样本选取时只考虑了降水和洪水极值之间的相关性，在后续的研究中还应增加其他气象要素进行洪水极值样本的综合选取，增加样本序列的覆盖程度。