具有多种治疗的HIV感染模型的最优控制

柳 玉，邓雄峰

(1.陕西铁路工程职业技术学院，陕西 渭南 714000；2.安徽工程大学高端装备先进感知与智能控制教育部重点实验室，安徽 芜湖 241000)

0 引 言

截至2020年底，全球约有3 770万艾滋病毒(HIV)感染者，其中非洲区域感染者的数量超过全球感染者总数的三分之二[1].HIV病毒主要攻击人体的CD4+T细胞，使得CD4+T细胞的数量逐渐减少，从而削弱人体免疫系统对机会性感染的免疫应答，最终导致艾滋病[2-3].2021年，全球约有2 820万HIV感染者接受抗逆转录病毒药物的治疗，其中药物主要包括逆转录酶抑制剂(RTIs)和蛋白酶抑制剂(PIs)[1].

近年来，众多学者研究传染病模型的最优控制问题，进而为临床治疗提供指导，其中传染病包括HIV、SARS、痢疾、肺结核和疟疾等.文献[3-8]考虑了使用RTIs和PIs两种药物治疗的HIV感染模型的最优控制问题.RTIs和PIs分别主要作用于阻断病毒感染CD4+T细胞和阻止感染性病毒的产生，但均未促进感染者自身免疫力的提高.1998年，KIRSCHNER D等[9]提出白细胞介素-2(IL-2)具有促使CD4+T细胞激活、增殖和分化的功能，并分析了IL-2治疗HIV感染的有效性.之后，CHATTERJEE A N等[10]考虑了使用RTIs和IL-2治疗HIV感染.2002年，JOSHI H R[11]基于文献[9]模型讨论了使用PIs和IL-2治疗HIV感染，模型如下：

(1)

其中：T(t)和V(t)分别表示t时刻血浆中CD4+T细胞和游离病毒的浓度；s1为CD4+T细胞的增殖率，s2为游离病毒对CD4+T细胞增殖的最大抑制率；μT为CD4+T细胞的自然死亡率；k为游离病毒对CD4+T细胞的感染率；g为游离病毒的最大输入率；c为CD4+T细胞对游离病毒的杀伤率；b1和b2分别为游离病毒抑制CD4+T细胞增殖和抑制游离病毒输入时的半饱和常数；v1和v2分别为IL-2和PIs两种药物的治疗效果.这里参数s1、s2、b1、b2、μT、k、g、c均为正数.

(2)

其中：u1(t)、u2(t)、u3(t)分别表示t时刻RTIs、PIs、IL-2三种药物的治疗效果，其余参数生物意义同模型(1).假设初始条件为

T(0)=T0≥0，V(0)=V0≥0

.

(3)

本文以在有限治疗时间内实现游离病毒的浓度和药物副作用尽可能小为目标，建立HIV感染模型的最优控制模型，该模型刻画了血浆中CD4+T细胞和游离病毒浓度的关系.通过Pontryagin最大值原理，得到对应的最优系统.利用反证法，证明了当治疗末端时间充分小时最优系统的解唯一.文献[4，5，10-12]中仅讨论了最优系统解的唯一性证明，但本文进一步给出末端时间充分小的估计式.此外，利用数值模拟进一步分析3种药物RTIs、PIs和IL-2组合治疗的最优控制策略以及有无治疗对细胞浓度的影响.模拟结果表明，3种药物的组合治疗能够有效提高CD4+T细胞的浓度且减少游离病毒的浓度.

1 最优控制问题的提出

经过一段时间的药物治疗，病毒通常会产生耐药性或发生突变，而且药物均存在副作用，故药物的治疗时间一般有限.本文讨论在有限治疗时间内使用RTIs、PIs和IL-2三种药物治疗HIV感染的优化方案.结合临床实际，人们通常期望实现游离病毒的浓度和药物治疗副作用尽可能小.定义目标函数

(4)

2 最优控制的特征

(5)

其中λ1和λ2为协状态变量.

(6)

横截条件为

λ1(tf)=0，λ2(tf)=0，

(7)

最优控制的表达式为

(8)

证明：利用Pontryagin最大值原理，由Hamilton函数(5)得协状态方程为

结果如式(6).由文献[14]得横截条件为λ1(tf)=0，λ2(tf)=0.

由模型(2)、初始条件(3)、协状态方程(6)、横截条件(7)以及最优控制的表达式(8)，得最优系统为

(9)

3 最优系统解的唯一性

引理1[15]设α、β为正常数，定义函数u(γ)=min{max{α，γ}，β}，则当α<β时，任取γ1、γ2∈，则有u(γ1)-u(γ2)≤γ1-γ2.

定理2当治疗末端时间tf足够小时，最优系统(9)的解唯一.

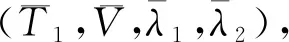
T=em tx1，V=em tx2，λ1=e-m ty1，λ2=e-m ty2，

(10)

(11)

其中m>0.进一步，得

由引理1和引理2，得

(12)

将式(10)分别代入最优系统(9)的4个方程，得

(13)

同理，将式(11)分别代入最优系统(9)的4个方程，得

(14)

根据引理2，上式等号右端的第3项和第4项可分别表示为

因此，有

(15)

将式(15)两端关于t在[0，tf]上积分并将等式右端放大，得

进一步，由MN≤(M2+N2)/2，得

(16)

其中，

同理，由系统(13)的第2个方程和系统(14)的第2个方程，得

(17)

其中，

(18)

将式(18)两端关于t在[0，tf]上积分并将等式右端放大，得

(19)

其中，

同理，由系统(13)的第4个方程和系统(14)的第4个方程，得

(20)

其中，

由不等式式(16)、(17)、(19)和(20)，得

由于上式的第1项恒非负，故

其中，

进一步，得

≤0.

(21)

为使不等式(21)左端积分项的系数均大于0，则m和tf需同时满足以下3个条件：

由定理2的证明可得，当m>max{m1，m2}时，若治疗末端时间tf满足0≤tf

4 数值模拟

利用数值模拟分析三种药物RTIs、PIs和IL-2的最优控制策略以及有无治疗对细胞浓度的影响.根据文献[11]，取治疗末端时间tf为50 d，初始条件为T0=400 mm-3，V0=3 mm-3.由文献[16]，权重取A1=A2=0.01.此外，由文献[11]知，A3约为A2的3 333至6 666倍，故本文取A3=50.其余参数取值见表1.

表1 最优系统(9)数值模拟的参数取值表Tab.1 Parameter values of optimality system (9)

在RTIs、PIs和IL-2三种药物的最优治疗策略下，观察图2和图3可知，在治疗的50 d内，CD4+T细胞浓度较无治疗明显增加，游离病毒的浓度明显减少.

图1药物最优治疗策略Fig.1The optimal controlstrategies图2有无治疗对CD4+T细胞的影响Fig.2The effect of treatmenton CD4+T图3有无治疗对游离病毒的影响Fig.3The effect of treatment onfree virus