水下爆炸下典型舰船结构整体损伤模式表征方法及图谱研究*

张 弛，刘 凯，李海涛，梅志远，郑欣颖

（海军工程大学舰船与海洋学院，湖北 武汉 430033）

为满足舰船快速性和不沉性的需要，世界海军水面驱护舰船逐渐向细长型方向发展，如近年美国服役的DDG-1000 型驱逐舰。现代驱护舰船细长型的设计特点导致其一阶湿频率约为几个赫兹。现代海战中水中攻击兵器主要为鱼雷、水雷。鱼雷主要通过直接命中船体产生直接杀伤，水雷主要采用中近场非接触爆炸对结构整体造成显著毁伤。水雷等非接触爆炸式兵器水中爆炸后的气泡脉动频率与细长型现代驱护舰船的湿模态频率接近，在若干倍数的气泡最大半径范围内，爆炸气泡和舰船之间形成强烈的耦合作用，容易导致舰船发生整体响应和破坏。在中距非接触爆炸下，这种响应表现为耦合弹性共振，出现鞭状响应，造成舰船总体大范围弹性变形；在近距非接触爆炸下，舰船则会发生整体塑性大变形，出现中拱或中垂损伤（统称为垂向损伤），甚至折断、沉没，影响范围广且造成严重后果。

近年来，国内外关于水下爆炸下舰船整体损伤特性研究逐渐增多，其中数值模拟研究作为一种有力的研究手段，对于解决复杂结构的非线性响应问题的能力突出，相关研究成果也较为丰富。Lee 等在Geer 提出双渐近法的基础上，推导了一种可评估声-结构相互作用问题的新近似方法，并通过实验验证了该方法在计算水中结构冲击瞬态响应中有较好的精度。王诗平等结合边界元方法修正Geer-Hunter 载荷计算方法，提出了非线性双渐近法，得以较好地处理低频流固耦合问题。刘云龙等建立了近场水下爆炸的欧拉有限元法，该数值模型可反映近场冲击波和气泡脉动的压力特性。针对模型实验，刘建湖等提出了一套水下爆炸舰船结构整体响应模型实验及载荷的缩比方法及模型实验设计流程，针对水下爆炸舰船整体响应各主要参数确定了各参数的缩比因子，并通过实验验证了利用该方法设计的缩比船体梁模型及实验工况在水下爆炸舰船整体响应研究中与实船响应具有一致性。姚熊亮等、宗智等、程远胜等、王海坤等采用ABAQUS 软件分别研究了舰船、典型船体梁等结构在近场不同爆距条件下发生整体中拱、中垂损伤时的响应过程，直观揭示了水下近场爆炸气泡作用下舰船的整体损伤模式，并利用模型实验验证了其数值方法的有效性。近场水下爆炸气泡在运动过程中会受到自由液面等边界的影响，其形成的射流冲击是气泡作用于船体结构的重要载荷。姜忠涛等、崔雄伟等针对水下近场爆炸气泡射流冲击外板结构开展了数值计算和实验验证研究，确定了射流的载荷压力特性和冲击速度特性，明确了射流对船体外板产生较大的剪切应力和剥蚀效应。贺铭等以双层破口结构受到水下爆炸气泡的作用为研究对象，通过气泡涌流速度、破口尺寸等参数对舰船结构抗冲击设计和生命力维持提供重要参考。

目前，水下中距、近距非接触爆炸作用下船体梁整体运动响应模式的种类已基本明确，大致可以分为中垂损伤、中拱损伤、鞭状响应及全弹性运动等几种类型。但关于水下爆炸强度和舰船整体损伤模式之间的关系仍有待进一步厘清，尚缺少合理表征爆炸载荷强度、结构强度的参数，并且此类参数与舰船整体损伤模式之间的关系也有待揭示，仍缺乏快速预报水下爆炸下舰船整体损伤模式的方法。

实现对水下中近距非接触爆炸作用下舰船整体变形及损伤模式的快速计算、评判及预报，对于优化水中兵器定向定位攻击方式、提升攻击效能及快速评判攻击效果均具有重要意义。针对以上问题，本文中综合研究水下中近距非接触爆炸冲击波和气泡载荷的影响，以水下爆炸下典型舰船/船体梁结构整体损伤特性数值计算研究为基础，提出合理表征水下爆炸强度和舰船结构强度的参数，建立水下爆炸载荷下舰船整体损伤模式的快速判定方法，实现了通过该两种参数可确定船体结构唯一整体损伤模式，提出一套快速评估水下爆炸下舰船整体损伤模式分布图谱的构建方法，以期为水面舰船设计、水中非接触式兵器攻击效能评估提供参考和借鉴，并进一步为鱼雷等接触爆炸兵器攻击方式选取和最大攻击效能设计提供参考。

1 数值模拟

1.1 有限元模型及参数

在水下爆炸下舰船整体损伤特性研究中，本文所选分析对象主要包括3 类：(1)两型实际驱护舰船；(2)与舰船主尺度相同且保证总纵惯性矩一致的实尺度船体梁；(3)保留了主要结构特征的简化缩比船体梁模型。根据Liu 等提出的方法及流程，本文中对缩比船体梁模型及其研究工况进行了设计，以保证其与实船整体响应结果具有一致性。使用Abaqus/Explicit 数值模拟软件，分别建立了缩比船体梁模型、实尺度船体梁模型及某典型驱逐舰、护卫舰实船模型。其中，船体结构采用shell 单元建模，划分单元为四边形结构网格，典型驱护舰船单元尺寸为0.5 m，实尺度船体梁单元尺寸为1 m，均小于纵骨间距。附连水域半径为船体半宽的6 倍，典型舰船计算对象的内层水域网格采用自由网格划分，耦合面处网格尺寸约为0.4 m，向外逐渐增大至2.0 m，外层水域网格采用映射网格划分，网格尺寸约为2.5 m。实尺度船体梁的附连水网格划分方法相同，水域耦合面处网格尺寸约为0.5 m，向外逐渐增大至1.0 m，外层水域网格采用映射网格划分，网格尺寸约为2.0 m。缩比船体梁网格尺寸对应缩比确定。计算均满足收敛性，数值计算模型如图1 所示。

图1 数值计算模型及网格Fig. 1 Numerical calculation models and meshes

根据Geer-Hunter 理论计算水下爆炸冲击波和气泡脉动阶段内流场压力曲线，作为载荷输入，分析起爆后结构响应过程。计算爆点位置处于水域范围之内，因此在加载时采用散波公式。将水作为声学媒介，其体积弹性模量为2.14 GPa，密度为1 000 kg/m，水中声速为1 500 m/s。船体梁模型采用Q235A 钢，材料本构模型及失效模型采用Johnson-Cook 模型，材料参数见表1。

表1 Johnson-Cook 本构模型及失效模型参数[18]Table 1 Johnson-Cook constitutive model and failure model parameters [18]

典型舰船和实尺度船体梁模型采用907A 钢，准静态屈服应力σ=390 MPa。材料本构模型采用Cowper-Symonds 模型，根据文献[19]，常数和分别为6 180 s和1.59。

数值计算时，选择瑞利阻尼法设置相应阻尼，其瑞利阻尼系数α、β 分别为：

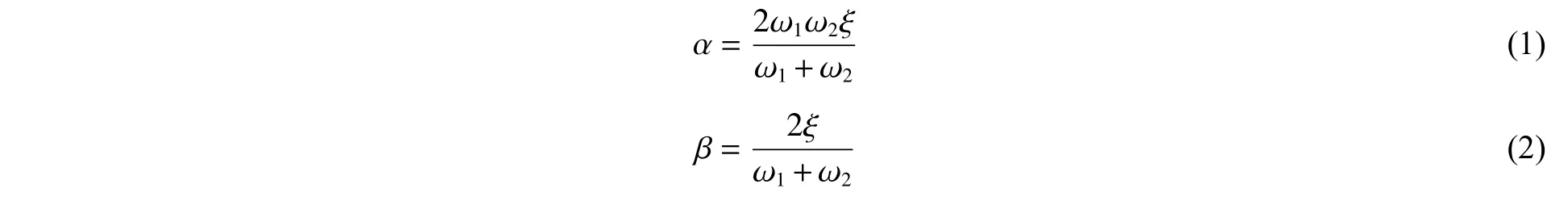
式中：ω、ω分别为一、二阶圆频率，rad/s；ξ为无量纲黏性阻尼比，一般取0.03～0.05。

1.2 数值方法的实验验证

为验证数值计算方法的有效性，以某型舰船为对象，以缩比模型与原型之间总纵强度相似、船体梁与爆炸气泡形成耦合效应，即缩比后梁模型一阶湿频率与缩比药量的爆炸气泡一阶脉动频率基本吻合，并参考文献[10-11]提出的相似性换算律设计了一种梯形横截面船体梁模型及其实验工况，开展水下爆炸实验。实验采用梁模型总长4 000 mm，宽度为300 mm，型高150 mm，其内部被横隔壁分成10 个小舱室，每个小舱室长度为400 mm；所有板厚均为1 mm；采用Q235A 普通钢制造。为保证吃水与实际情况相当，在除艏艉舱壁的其他横舱壁上焊接不同质量的铁块。配重后梁总质量为71.52 kg，其中配重质量为42.00 kg。梁模型及具体配重情况如图2 所示。通过力锤实验法测得梁模型一阶湿模态频率为22.2 Hz，二阶湿模态频率61.9 Hz。

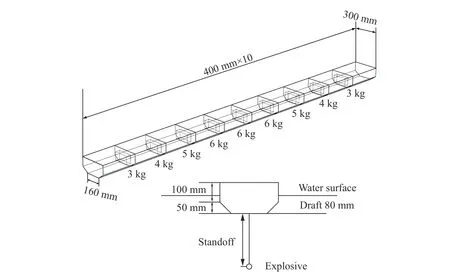
图2 船体梁模型及水下爆炸实验布置示意图Fig. 2 Schematic of girder model and underwater explosion experimental layout

实验水深为3.0 m，梁模型自由漂浮于水面，吃水约80 mm。采用TNT 炸药作为爆源，置于船体梁下方爆炸。为了验证有限元模型的有效性，选取某典型爆炸工况进行数值计算，工况参数为：药量为0.006 kg、爆距为0.30 m、最大气泡半径为0.28 m，第1 次脉动频率为19.7 Hz，爆径比γ=/为1.06。其中和根据相关文献[20]中的计算公式得到。

实验时，利用高速摄影仪从水面上拍摄记录水下爆炸下船体梁响应过程，其拍摄频率为250 s。随着气泡的膨胀和收缩，船体梁模型均出现不同幅度的上下升沉运动，并叠加整体中拱、中垂弯曲变形。通过高速摄影照片分析船体梁的运动过程，并将数值计算结果与实验结果对比。

船体梁的运动过程对比如图3 所示。根据响应过程高速摄影照片观察出，在冲击波及第1 次气泡脉动期间（约50 ms），船体梁的整体变形较大，梁呈现先中拱弯曲、后中垂弯曲的运动变形过程。炸药爆炸后（0 ms），初始冲击波短时扩展开去，强大的压力作用于结构，气泡随之开始快速膨胀，推动滞后流运动并以动能的形式作用于船体梁底部，冲击波和气泡膨胀导致船体梁出现中拱变形；气泡不断膨胀，内部压力逐渐减小，当内外压力相等时，船体梁中部出现约23.0 mm 的最大相对中拱变形，计算值为24.8 mm；随后气泡因惯性作用继续膨胀，其内部压力逐渐低于外部压力，导致船体梁中部受压开始向水平状态变化；28 ms 时刻，气泡膨胀到最大，船体梁基本回复至水平状态；随后，气泡在外部正压作用下收缩，且气泡脉动频率与结构湿模态频率相近，耦合共振被激发，与内外压差产生的负压共同作用使结构继续向中垂弯曲状态变化，气泡快速收缩进一步加快其中垂变形速度，最终产生中垂变形；48 ms 时，船体梁中部出现约69.0 mm 的最大相对中垂变形，对应的计算值约为73.1 mm。最终船体梁发生永久中垂塑性弯曲破坏，中部出现一个固定塑性绞，最大中垂变形量约为138.0 mm，计算值135.5 mm，误差2%。距梁端部800.0 mm 区域内的计算位移与实验值十分接近，偏差不超过4.0 mm。参见图4～5，得出梁结构整体的位移计算误差不超过10%。

图3 船体梁中部垂向运动过程实验与数值模拟对比图（正值为中拱变形，负值为中垂变形）Fig. 3 Comparison between experiment and simulation process of vertical movement at middle of girder (positive value represents hogging deformation; negative value represents sagging deformation)

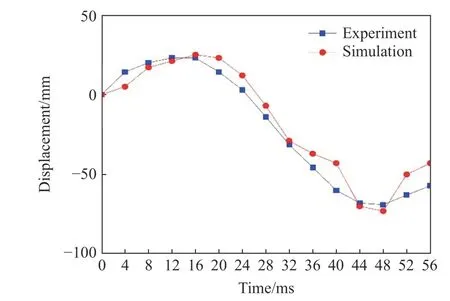
图4 船体梁中点位移时程曲线数值结果和实验结果对比Fig. 4 Comparison between numerical and experimental displacement-time curves at the girder’s mid-point

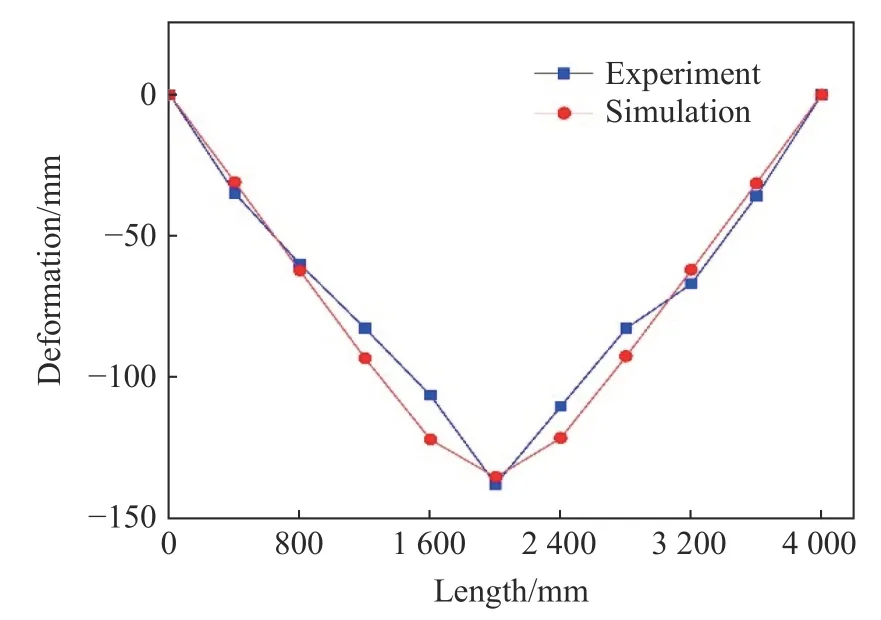
图5 沿长度方向船体梁垂向变形数值结果和实验结果对比Fig. 5 Comparison between numerical and experimental girder’s vertical deformations along longitudinal direction

利用VTOP780H 型三维激光扫描仪对实验后的船体梁损伤变形情况进行扫描、建模，提取变形数据及特征，并与数值计算结果进行比较，如图6 所示。水下爆炸载荷作用下，船体梁中部底板发生局部内凹变形，其最大变形的实验值为19.8 mm，对应的计算值为19.4 mm，相对误差为2%。

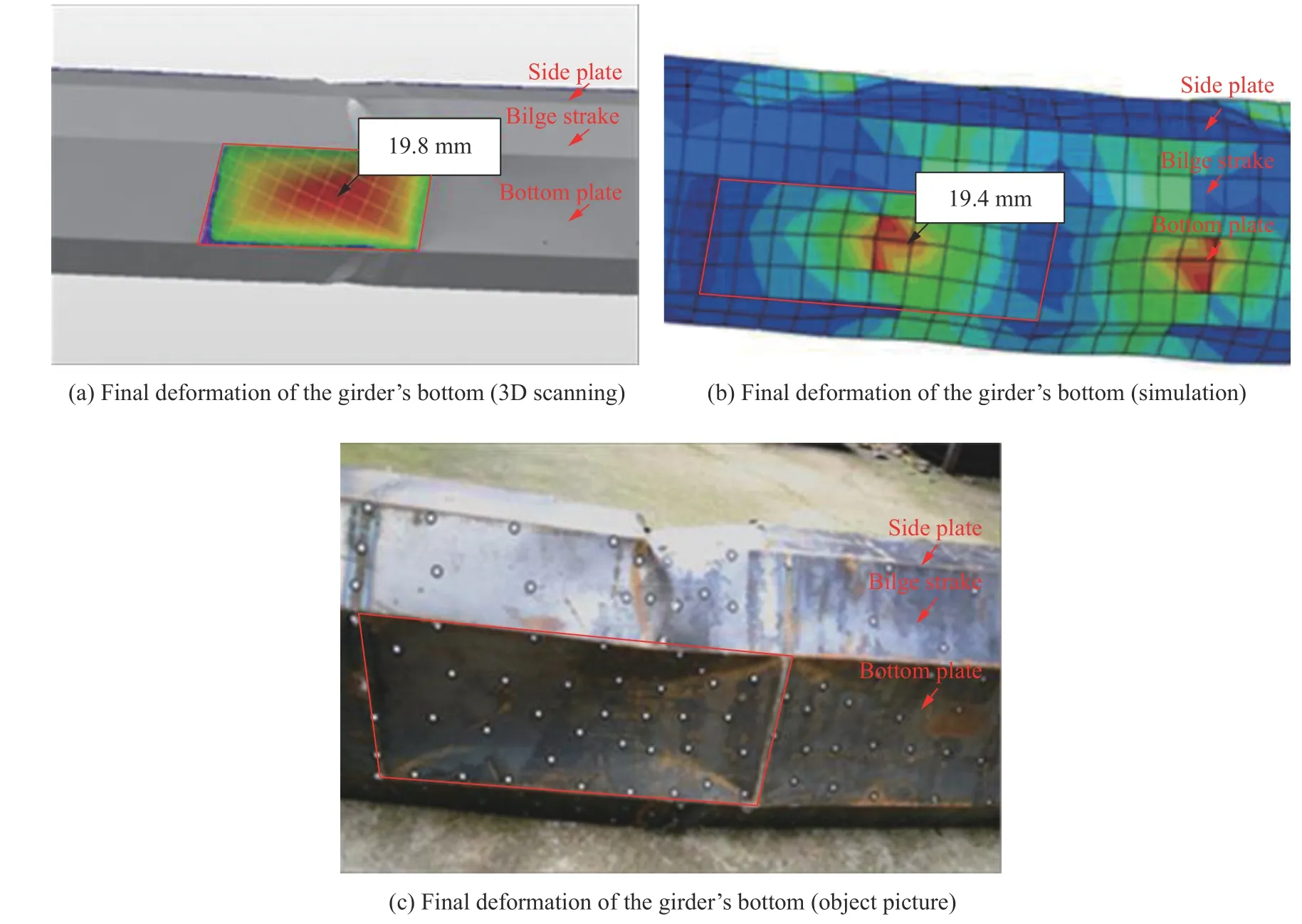
图6 船体梁底部最终变形数值模拟和实验结果对比Fig. 6 Comparison between numerical and experimental final deformation of the girder’s bottom

综合图3～6 给出的实验和数值计算结果的对比情况可以看出，本文中建立的数值计算方法能较好模拟水下爆炸下船体梁整体及局部损伤响应过程，对其损伤模式和变形量均具有较高的预报精度，验证了数值方法的有效性。

1.3 数值计算结果

在上述数值计算方法的基础上，以典型缩比船体梁、实尺度船体梁、实际舰船作为分析对象，通过改变水下爆炸强度和攻击方位，研究不同爆炸工况下典型舰船结构的整体损伤特性。图7 中给出了水下爆炸点位布置示意图。沿舰船纵向布置时，所有爆点均位于舰船中纵剖面上，即位置点的横向坐标均为0。爆点横向布置时，包括正下方爆炸和攻角α 为45°的工况。

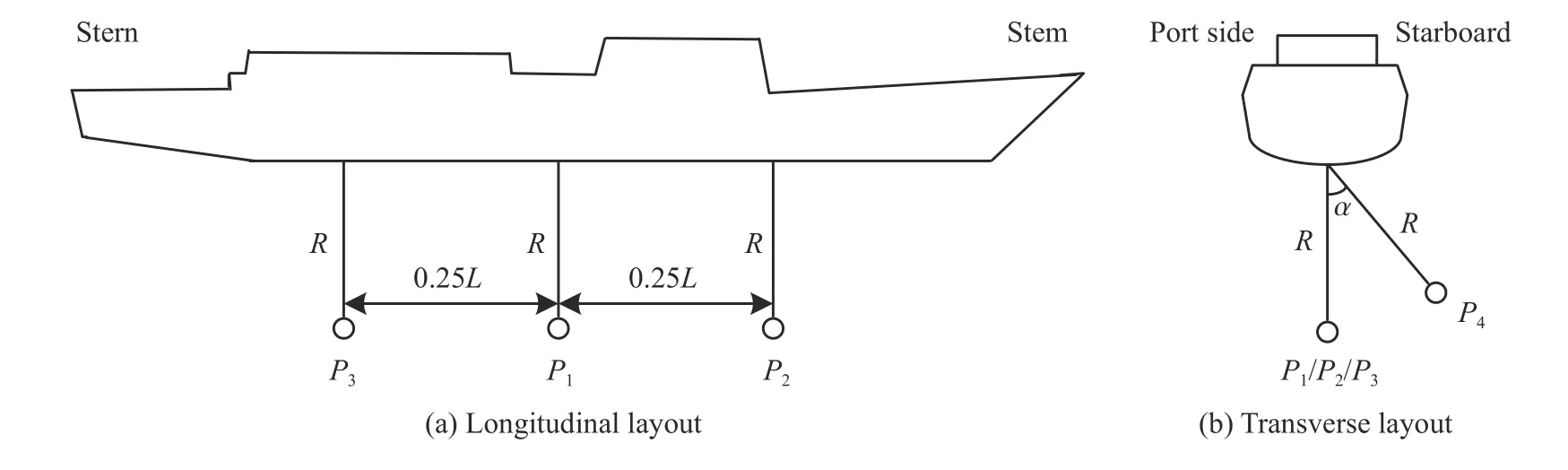
图7 水下爆炸计算工况纵、横向点位布置示意图Fig. 7 Schematic of longitudinal and transverse layout of underwater explosion calculation case

两型船工况均一致，采用W-P-R的形式。为炸药TNT 当量，为爆距，为爆点，为船长，并给出以下定义：(1)爆点位于船舯正下方；(2)爆点位于距船艏0.25处；(3)爆点位于距船艉0.25处；(4)爆点位于船舯、攻角为45°（右舷）的位置。举例：W--R表示炸药当量为、爆点位于距船艉0.25处、爆距为的工况。

使用前述建立的ABAQUS/Explicit 数值方法分析该典型爆炸工况下驱护舰船的整体损伤特性，隐去了具体工况及对应结果。舰船结构整体损伤模式示意如图8 所示。

图8 典型舰船中拱/中垂损伤模式示意图Fig. 8 Schematic of hogging and sagging damage mode of typical warship

通过对各工况进行数值计算，获得了典型舰船响应后的运动过程和响应模式。在水下爆炸冲击波和气泡脉动载荷下，典型舰船总体响应过程及损伤模式相似。首先，船体在初始冲击波作用下，船底外板和舷侧外板均出现了局部内凹变形，但整体中拱变形并不明显；随后，气泡脉动引起的流场低压效应导致船体发生中垂损伤变形。当药量和爆炸方位一定时，爆距的改变主要影响爆径比γ。在近距爆炸下，舰船结构出现显著的垂向整体损伤，当爆炸位置接近舰船结构（γ＜0.4），爆炸冲击波其气泡膨胀将造成舰船发生较为明显的整体中拱损伤并伴随底部板架局部凹陷变形；随着爆径比的逐渐增大至约一倍气泡最大半径，气泡脉动形成的低压流场将对舰船整体造成明显的中垂损伤破坏。当爆径比进一步增大（γ 约为2.5），中距爆炸气泡运动引起的低压流场对船体的总体损伤效果逐渐减弱，船体响应由永久中垂塑性损伤逐渐发展至“鞭状运动”；继续增大爆径比时（4＜γ＜6），舰船将仅发生弹性运动变形。

当药量和爆距相同时，通过改变爆炸方位，仅各工况中距离爆点位置最近的板架结构出现局部破坏，但舰船最终整体损伤模式不发生改变。当爆炸方位和爆距一定时，一般情况下，相比小药量爆炸，大药量爆炸带来的较高的冲击波压力峰值和较小的爆径比可能造成船体出现较严重的局部板架损伤和船体整体损伤变形。在一些临界工况下，即小药量爆径比略高于0.4 时，根据上述影响规律，大药量爆炸导致的爆径比的减小可能会改变整体损伤变形模式，但是局部损伤程度仍然强于小药量爆炸。

2 冲击强度与结构整体损伤的关系分析

大量研究已证明，当水下中近距爆炸发生于舰船底部时，爆炸冲击波和气泡载荷会对舰船结构造成不同程度的整体损伤，尤其以近场非接触爆炸更为明显；爆炸载荷与舰船结构响应之间存在明显的耦合关系。为揭示以上内在联系或规律特征，本文以前期研究为基础，初步提出如下分析思路和假设：(1)舰船的整体响应程度以中部结构响应大小为考核依据，以中部结构的最大中拱和中垂变形值之比作为确定其最终整体损伤模式的依据；(2)水下爆炸强度需要综合考虑冲击波和气泡载荷，其联合强度可用单一函数因子表征；(3)舰船结构整体强度可以用单一函数因子表征，该因子应包含结构典型尺度参数；(4)爆炸气泡与舰船结构之间存在耦合作用，耦合程度可用函数因子表征，是两者频率比值的函数；(5)整体损伤表征参数与函数因子、和之间存在某特定函数关系。

基于以上思路和假设，通过分析计算确定以上参数之间的函数关系，成为揭示水下爆炸载荷和舰船结构整体损伤之间关系的主要途径。

2.1 冲击波或气泡单一强度因子

当前，行业内通常分开表征水下爆炸冲击波或气泡载荷的强度。关于冲击波，前人定义了表征水下爆炸冲击波强度的冲击因子，对同一结构，若冲击因子相等则认为其水下爆炸冲击响应近似相等。常用的主要表征爆炸冲击波强度的冲击因子目前主要有3 种。

(1)基于冲击波压力峰值的冲击因子：

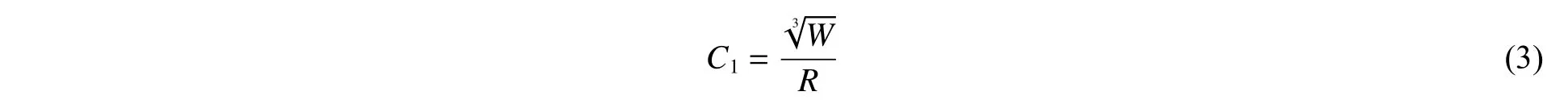
(2)基于平面波假设的冲击因子：

(3)考虑平面波假设的球面波修正的冲击因子：

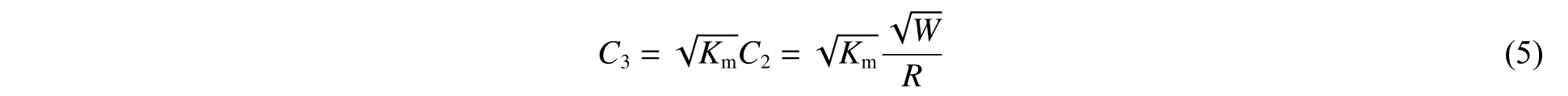
式中：为炸药质量，kg；为爆心距离结构的最短距离，m；K为修正因子。

冲击因子主要反映冲击波压力峰值，当小药量于超近场爆炸时所产生的峰值压力有可能比大药量远距离爆炸时的大，但是它对舰船结构产生的破坏不一定大，其难以反映水下爆炸结构冲击环境的相似性，目前应用较少。冲击因子主要反映基于平面波假设且结构遮挡的冲击波能量，亦称为平板冲击因子（hull shock factor, HSF）。考虑垂向冲击响应且炸药位于非正下方爆炸情形时，需要定义冲击波入射相对船体龙骨基平面的角度θ，即龙骨冲击因子（keel shock factor, KSF）：

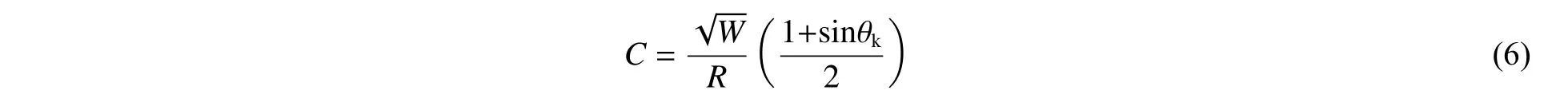
该因子考虑了爆炸方位等因素且形式简单易于计算，但在本文所研究的近场爆炸中，平面波假设不成立，该因子与环境相似过程中存在较大误差。冲击因子主要考虑球面波效应后对平面波假设冲击因子的修正。冲击因子可以较好反映近场爆炸环境，但其所涉及参数太多，计算复杂。

以上仅从冲击波角度对爆炸强度进行表征。研究发现，水下爆炸气泡携带了近一半以上的爆炸能量。对于舰船整体损伤而言，水下爆炸气泡脉动冲击作用明显，需考虑其带来的损伤影响。气泡的最大半径与爆距(爆炸深度)密切相关，李海涛等、Li 等提出常用爆距与首次脉动气泡最大半径的比值，即爆径比γ 来表征结构边界对水下爆炸气泡脉动的影响，且该参数可直接影响到气泡射流方向和强度等特性。

2.2 结构强度因子

通常使用舰船典型横剖面惯性矩来表征其总体抗弯能力，但由于其形式过于简单，无法反映截面高度、宽度、板厚等其他结构尺度参数的影响。且对于缩比模型而言，其截面惯性矩与实船截面惯性矩存在数量级的差别，无法在同一个尺度坐标上表征。为此，本文从船体梁截面惯性矩理论计算公式出发，选取典型横截面形式，在将截面纵向构件进行板厚尺度等效的基础上，推导了梁截面总纵惯性矩与截面型深、型宽、板厚之间的函数关系，为简化形式保留了高阶指数项，定义无量纲化的表征舰船/船体梁结构强度因子为：

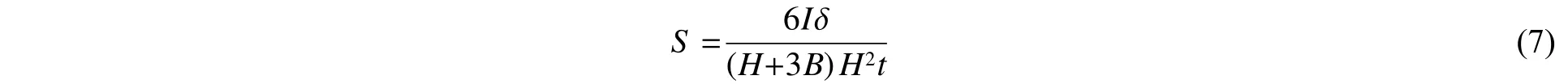
式中：为典型截面惯性矩，m；为型宽，m；为型深，m；为板厚，m；δ为无量纲船型系数，在数据处理中根据经验获得。

2.3 冲击波和气泡联合强度因子

综合考虑水下爆炸冲击波和气泡脉动联合作用及气泡脉动与船体结构耦合效应对舰船整体损伤模式的影响，建立能综合表征水下爆炸冲击波和气泡载荷强度及损伤效果的新型冲击因子。为表征冲击波与气泡联合作用下的载荷强度，选用广泛使用且形式较为简单的基于平面波假设的冲击波强度因子和表征气泡脉动强度的爆径比γ 构成新型冲击因子。通过前期单一参数变化对舰船结构整体响应的影响规律研究可知：当冲击波强度因子增大时爆炸冲击波强度较大，当爆径比γ 增大时结构损伤效果减弱。为此，兼顾两者的综合作用，同时考虑无量纲化，初步得到新的无量纲综合冲击因子为：

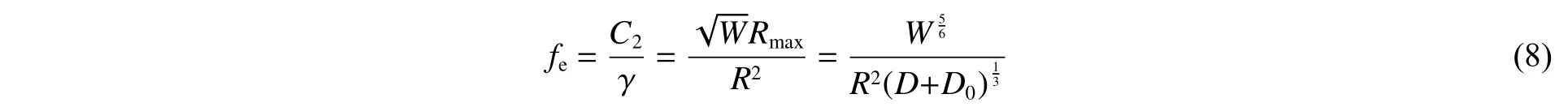
研究表明，当气泡脉动频率与结构一阶湿模态频率相近时，结构的耦合共振容易被激发出来，该耦合特征是一个不可缺少的重要因素。为反映气泡脉动与船体结构耦合效应对其整体响应的影响，定义一种表征耦合效应的因子，认为其是频率比的函数，其形式如下：

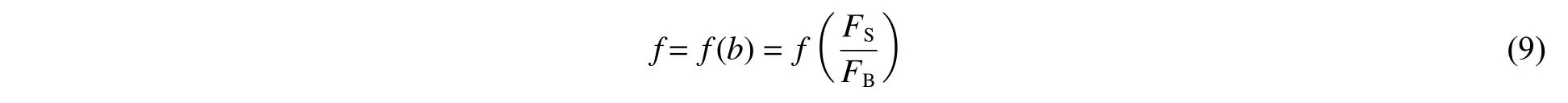
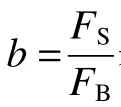
以前述3 类结构对象在不同水下爆炸工况下的计算结果为依据，结合各工况下的参数和值，反算出耦合因子，观察其数据分布并进行二次多项式拟合初步获取无量纲频率耦合因子：

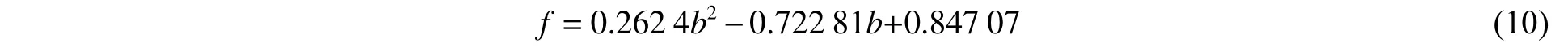
综合以上因素，提出一种综合考虑冲击波和气泡脉动联合作用强度及气泡与结构耦合效应的新型冲击因子，如下式所示：

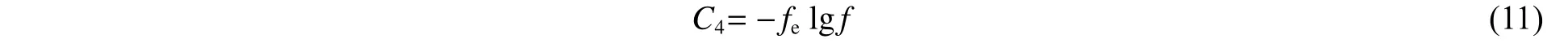
3 整体损伤图谱构建

以上述结构强度因子和爆炸冲击强度因子为纵、横坐标，分别梳理本文不同计算工况中的数值计算结果及前期部分研究数据，构建不同的舰船结构整体损伤模式分布图谱，并对其分布特征进行比较分析，具体情况如下。其中结构强度因子的具体数值已进行脱密处理。

3.1 爆径比-结构强度因子整体损伤模式分布图谱

以爆径比γ 作为横坐标，结构强度因子作为纵坐标，列出前期数值计算及实验工况下实船及梁损伤模式分布情况，如图9 所示。

图9 爆径比-结构强度因子整体损伤模式分布图谱Fig. 9 The ratio of standoff and maximum bubble radius-structural strength factor overall damage mode distribution atlas

可以看出，所涉及的研究对象中，其结构因子大致分布在3 个区间。3 种结构对象的结构强度因子分布比较合理，较好地体现了其抗水下爆炸冲击损伤的能力。所有典型爆炸工况的爆径比γ 的变化范围为0.2～6.0，为水下非接触中近场爆炸。随着γ 的增大，各类结构的损伤模式基本呈现从中拱损伤到中垂损伤再到鞭状响应的变化过程。其中，当γ＜0.4 时，各类结构以中拱损伤为主；当0.4＜γ＜2.5时，损伤模式以中垂损伤为主，包括轻微中垂塑性损伤；当γ＞2.5 时，结构以鞭状响应或弹性响应为主。总体而言，利用爆径比γ 来表征舰船或船体梁的整体损伤，具有一定的合理性，其区分度比较明显，但少部分工况的损伤模式仍存在交叠现象。例如，前期方形截面船体梁缩比模型实验研究中，在同样的爆径比γ 为1 时，5 g TNT 炸药爆炸造成梁中垂损伤，而30 g 和55 g TNT 爆炸却造成梁中拱损伤，这也表明绝对药量对结构损伤模式的影响较大，单纯通过爆径比来判断整体损伤模式仍存在一定不足。

3.2 球面波修正的冲击因子-结构强度因子整体损伤模式分布图谱

以目前较为完备的考虑平面波假设的球面波修正的冲击因子作为横坐标，结构强度因子作为纵坐标，列出前期各工况下舰船/船体梁损伤模式分布情况，如图10 所示。

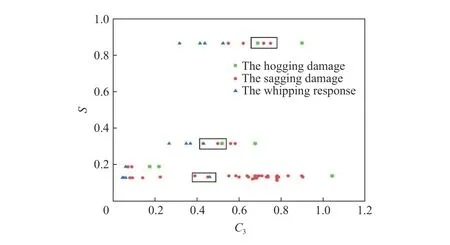
图10 球面波修正的冲击因子-结构强度因子整体损伤模式分布图谱Fig. 10 The shock factor of spherical wave correction-structural strength factor overall damage mode distribution atlas

从横坐标来看，所有典型爆炸工况冲击因子的变化范围为0～1；随着的增大，各类结构的损伤模式基本呈现从鞭状响应到中垂损伤再到中拱损伤的变化过程，但部分工况的损伤模式存在交叠现象（图中方框内），一致性分布规律不明显，初步表明，仅利用冲击波强度因子来表征舰船或船体梁的整体损伤，还存在一定困难。

3.3 新型冲击强度因子-结构强度因子整体损伤模式分布图谱

以新型冲击强度因子作为横坐标，结构强度因子作为纵坐标，列出前期数值计算及实验工况下实船及梁损伤模式分布情况如图11 所示。

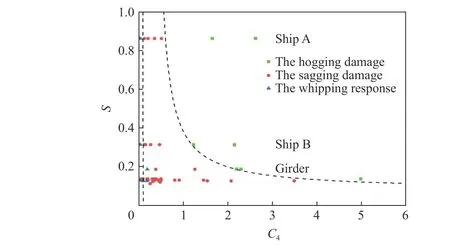
图11 新型冲击强度因子-结构强度因子整体损伤模式分布图谱Fig. 11 The new shock factor-structural strength factor overall damage mode distribution atlas

可以看出，所研究典型爆炸工况的冲击因子的变化范围为0～6。各研究对象的结构强度因子在图谱上分为3 类，如图标注。对于同类结构，随着的增大，其损伤模式基本呈现从鞭状响应到中垂损伤再到中拱损伤的变化过程。

分析两型实船工况，在4 种爆炸位置中均设置了一大一小两型药量及近中远3 种爆距。在小药量的情况下，在不同爆炸方位起爆，随着爆距的减小，舰船整体响应依次呈鞭状响应、中垂损伤、中拱损伤，其对应的爆径比参数减小（分别为5.5、1.0、0.4）、龙骨冲击因子增大（分别为0.5、2.5、4.0），与前期研究得出的损伤影响规律一致。同时，计算得出本文新提出的因子亦是随之增大的，因而出现图谱中随着持续增大，结构响应由鞭状响应向中垂损伤、中拱损伤转变的趋势。大药量工况中该影响规律及损伤模式保持不变，但结构整体损伤程度有一定提升，其爆径比参数比小药量爆距工况下的爆径比还略小，且龙骨冲击因子略大，计算出的亦对应增大。

针对船体梁模型，在研究上述爆炸参数对其整体损伤形式的影响之外，加入了船体梁各结构尺度参数变化对其影响，即结构强度变化对整体损伤模式分布的影响，因此船体梁对应的强度因子存在一定的散布。一般情况下，强度因子是某型船的固有属性不会产生变化。

观察图谱数据点分布看出，在爆炸强度相当且较小的情况下（＜0.1），各类研究对象不易出现整体塑性大变形，而是以弹性或鞭状响应为主。当0.1＜＜1 时，各研究对象主要发生中垂变形。当＞1 时，不同研究对象出现不同的损伤形式：结构强度因子较高的实船在初始冲击波能量的强烈作用下形成中拱变形，气泡负压无法将其反折，最终形成永久性中拱损伤；结构强度因子较小，相对较弱的船体梁（实尺度和缩比模型）对气泡脉动产生的负压抵抗能力较弱，在受到冲击波作用出现中拱变形之后，气泡脉动更易于将其反向弯折成中垂损伤模式，因而呈现较宽的中垂损伤区域，其发生中拱损伤的起始值较大。

综合来看，相比于因子，利用冲击因子来表征舰船或船体梁的整体损伤划分，其对应的内在变化规律与前期关于龙骨冲击因子、爆径比、爆距、药量等参数影响规律研究结论一致，绘制而成的分布图谱区域分隔比较明显，损伤模式交叠现象不突出，有利于对不同爆炸工况下舰船/船体梁整体损伤模式的快速判断。从工程应用角度而言，该图谱具有一定的合理性和参考应用价值。

4 结 论

通过对水下中近距非接触爆炸下典型驱护舰船结构整体损伤模式的研究，在本文所涉及的水下爆炸冲击环境范围（0.2＜γ＜6）内，主要得到以下结论：

(1)基于Abaqus 数值软件建立了水下爆炸下舰船整体损伤数值计算模型，并通过梯形截面船体梁模型水下爆炸实验验证其有效性；所建立数值计算方法能较好预测舰船结构整体损伤模式和总体变形，误差不超过10%。

(2)本文基于大量研究数据，全面考虑影响总体结构强度的主要结构参数（型高、型宽、板厚、惯性矩等），定义更加全面表征舰船/船体梁结构强度的因子，代替原先单一的截面惯性矩来表征其总体抗弯能力。

(3)综合基于平面波假定的冲击波强度因子、爆径比参数γ 以及通过数据拟合出可表征气泡与舰船结构的耦合因子，首次提出了表征水下爆炸冲击波和气泡脉动联合作用下的冲击强度因子。

(4)利用新型冲击强度因子和结构强度因子建立了一种快速构建舰船/船体梁整体损伤模式分布图谱的方法，所建立的损伤模式分布图谱能较好区分不同爆炸强度、舰船结构强度下的舰船整体损伤模式分布特点，具有一定的工程应用价值。