认知异构蜂窝网络中改进蜉蝣算法的资源分配策略

张达敏，王义，邹诚诚，赵沛雯，张琳娜

（1.贵州大学大数据与信息工程学院，贵州 贵阳 550025；2.贵州大学机械工程学院，贵州 贵阳 550025）

0 引言

随着信息社会科学的快速发展，移动终端用户数量呈爆炸式增长，用户服务质量（QoS,quality of service）需求激增，传统的以宏蜂窝为单元的单小区蜂窝网络已经很难应对当前终端用户激增的挑战，网络覆盖面积不足、用户分布的“热点”和“盲点”问题明显，网络拥塞现象难以得到有效控制；据美国联邦通信委员会报道，以固定式接入资源频谱方式利用率低下，约为15%～85%，更多资源未使用造成频谱资源浪费[1]。为解决资源复用利用率低的问题，1999 年，Mitola 等[2]首次提出了认知无线电（CR,cognitive radio）技术。该技术将用户类别分为已授权的主用户（PU,primary user）和未授权的认知用户（SU,secondary user），将未授权的SU 机会式地接入PU 频段空闲资源，能有效避免资源浪费，提升资源利用效率。CR 技术自提出以来，就受到大量通信领域研究者的重视。

显然，传统的宏蜂窝网络已不能满足通信用户日益增长的需求；为满足通信网络的可持续发展、千倍级的容量提升和绿色通信的需要，异构蜂窝网络逐渐成为解决传统蜂窝网络针对性覆盖率低和数据速率需求日益增长的有效技术手段。遗憾的是，异构蜂窝网络的资源复用依然是固定式接入信道方式，资源有效利用率低。随着对CR 技术的深入研究，研究者借助CR 技术优势，在异构蜂窝网络中宏蜂窝覆盖区域部署认知家庭基站（CFBS,cognitive family base station），形成融合CR 和异构技术的认知异构蜂窝网络[3]，感知空闲资源并机会式地接入，达到提升通信上行容量和资源利用率的目的；与异构蜂窝网络相比，引入CR 的异构网络能使认知家庭用户（CFU,cognitive family user）更好、更公平地接入CFBS，为不同用户接入提供高效的QoS 需求，是改善通信网络技术的重要手段。

目前，对于网络的资源分配问题，已有相关研究者进行深入研究，大部分采用的求解方案为博弈论算法[4-5]、拉格朗日的 KKT（Karush-Kuhn-Tucker）条件法[6-7]、拍卖方法[8]、图论着色模型[9]和智能算法[10-11]等，这无疑为资源分配问题的求解提供了更多方案。董晓庆等[11]在认知异构无线网络中利用遗传算法（GA,genetic algorithm）求解资源分配问题，以最大化用户传输速率为目标，得出与其他算法相比利用遗传算法求解的优势，实验证明了智能算法模型在解决这类问题的优越性，但该方法一味地追求不同用户业务需求的传输速率，并没有考虑网络中干扰和功率的影响。Hasan 等[12]针对5G 多异构的网络重叠，按照PU 的接入特性和SU 需求，使用改进的遗传算法和粒子群优化（PSO,particle swarm optimization）算法求解资源分配问题，实验取得了较好的效果，但并没有考虑资源异构问题，应用场景相对简单。对于认知异构蜂窝网络的最大化能效优化问题，庄陵等[7]在考虑带内干扰、层间干扰和实时用户QoS 的基础上，利用拉格朗日松弛法优化最大化能效，分析干扰问题，但并没有为干扰提出有效的解决方案，造成系统中干扰较大。吕威等[13]考虑认知异构网络系统中功率控制策略来降低系统干扰，利用非合作博弈论算法分析了系统干扰问题和能效问题，但整体而言该算法复杂度较高。Xu 等[14]在异构认知无线电网络中采用非正交多址接入（NOMA,non-orthogonal multiple access）技术以用户最大化传输速率和最大化带宽为目标系统分析了网络性能，利用k-means 算法求解取得了较好的资源分配效果，但干扰问题还是难以得到有效抑制。Xu 等[15]在认知异构网络中考虑用户接入公平性的资源分配方案，实验为用户取得了良好的公平性，但是场景简单、网络的仿真实验中用户数量较少，接入一般网络场景性能不一定能得到保证。

对于认知无线电和异构无线网络融合的资源分配问题已在国内外取得较多研究成果，但都主要考虑异构网络中用户传输速率、信干噪比、功率控制、能效优化等关键绩效指标。虽然都是值得肯定的研究成绩，但依然还有很多未考虑的地方，如单一的指标得到提升但并未考虑用户QoS 等缺陷，用户的体验质量（QoE,quality of experience）并未得到各方面的满足。因此对于更好的用户QoS 而言，资源分配问题还存在很大的完善空间。针对认知异构蜂窝网络中考虑用户QoS 的资源分配问题，本文利用改进离散的蜉蝣算法（MA,mayfly algorithm）[16]对含QoS 约束的资源分配求解，而MA的优势主要在于该算法具备与PSO[17]、GA[18]和萤火虫算法（FA,firefly algorithm）[19]已有的优势，是3 个算法的融合，但算法的深度融合并没有明显提升算法的时间复杂度。因此，本文基于认知异构蜂窝网络，做出以下工作内容来提升网络性能。

1) 为满足通信网络发展的绿色需求、提升网络传输质量，降低认知异构蜂窝网络中的干扰成为需要解决的关键问题之一。由此，在网络初始化阶段引入开环功率控制（OLPC,open-loop power control）策略控制发射端功率，引入闭环功率控制（CLPC,close-loop power control）策略对用户发射功率动态调整，以达到降低干扰的目的，获得更好的传输需求；在干扰分析中，考虑层间干扰和带外干扰问题，为保证用户具有可靠的传输速率，在用户接入时优先选择具有可靠传输速率的资源复用，满足用户QoS 保证；将CFU 划分为实时（RT,real time）和非实时（NRT,non-real time）用户集合，在资源复用时，优先为CFU 中的RT 用户分配资源。

2) 对认知异构蜂窝网络资源分配问题的求解，引入黄金正弦与自适应权重的离散二进制蜉蝣算法（GSWBMA,gold-sine and weight binary mayfly algorithm）求解。首先将MA 位置进行二进制离散化，转化为离散的二进制蜉蝣算法（BMA,binary mayfly algorithm），MA 与其他智能算法一样，求解精度低，因此在MA 中引入不完全Gamma 和Beta函数自适应动态权重策略，使算法能自适应地动态调整搜索趋势，提升算法搜索性能。其次，引入黄金正弦策略，在算法中引入黄金分割算子，借助繁殖阶段的交配行为作为黄金分割因子重新更新算法的速度和位置，提升算法收敛性能和精度。最后，通过GSWBMA 求解资源分配问题，实验表明GSWBMA 求解的有效性和优越性。

1 认知异构蜂窝网络模型与问题描述

1.1 网络系统模型

本文主要考虑认知异构蜂窝网络上行链路模型，以Overlay 模式接入频谱，系统模型如图1 所示。其中，认知异构蜂窝网络中包含一个覆盖范围最广的宏蜂窝基站（MBS,macro-cell base-station）、S个CFBS、M个宏蜂窝用户（MU,macro-cell user）和F个CFU。每个CFBS 服务1～10 个CFU，且MU 和CFU 随机分配在各自的小区，CFBS 随机部署在 MBS 区域范围内，设正交频分多址接入（OFDMA,orthogonal frequency division multiple access）的总带宽为W，将其平均分为N个子信道，每个子信道所占用的带宽为。同时，每个子信道都服从相同的瑞利衰落和路径传输损耗模型。由文献[14]的路径损耗模型可知，认知家庭用户i的路径损耗模型定义为

图1 认知异构蜂窝网络系统模型

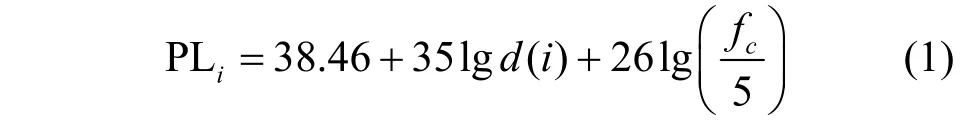
其中，PLi为第i个认知家庭用户的路径损耗，d(i)为认知家庭用户到CFBS 的距离，单位为m；fc为子载波频率，本文取2 GHz。根据文献[20]，信道增益由路径和快慢衰落共同确定，其信道增益模型可表示为

其中，K为常数，根据系统的参数确定；β为快速衰落增益系数，服从1－λ=的指数函数分布；σ为服从对数正态分布的慢衰落增益；d为用户到基站的距离；α为路径损耗指数，取值为4。

在异构蜂窝网络的业务场景，CFN 存在RT 业务和NRT 业务，2 种业务集合记为GRT和GNRT。本文主要目的是满足用户需求的QoS 保证和干扰约束下最大化认知异构蜂窝网络性能，RT用户较NRT用户拥有优先接入权。设表示第s个CFBS 中第f个CFU 在第n个子信道上到MBS 的信道增益，表示第s个CFBS 中第f个CFU 在第n个子信道上到CFBS 的信道增益，表示第m个MU 在第n个子信道上到CFBS 的信道增益，则第f个CFU 在第n个子信道上的信干噪比（SINR,signal to interference plus noise ratio）为

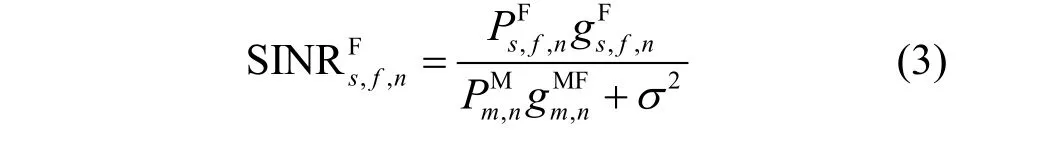
其中，σ2为系统的加性白高斯噪声，分别为CFU 在第s个CFBS 中的第f个子载波在第n个信道上的发射功率和第m个宏蜂窝用户在第n个信道上的发射功率，为宏蜂窝用户对认知家庭用户通信造成的层间干扰。由香农公式可知，在第f个子载波上的第n个信道上的传输速率为

认知无线电网络中，MU 享有资源接入的优先权。此外，为保证MU 的可靠资源接入，其SINR 需满足

CFBS 的传输功率需满足

由于硬件设施限制MBS 为CFBS 提供的传输功率预算为，则CFBS 允许的最大传输功率为

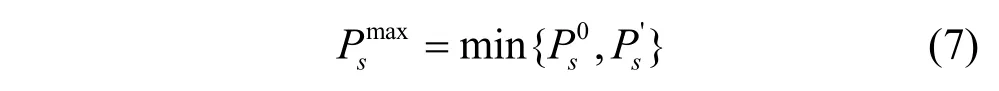
在认知异构蜂窝网络中，除了用户间的层间干扰外，通信过程中由于Overlay 方式的频谱接入过程中会发生旁瓣功率泄露现象，因此CFU 还会对MU 产生带外干扰[7]。由文献[15]的干扰模型可知，CFU 在第n个信道上对宏蜂窝网络占用的子信道造成的带外干扰为

其中，φn(f)为信号的功率谱密度，和分别为2 个子信道的中心频率，φn(f)为

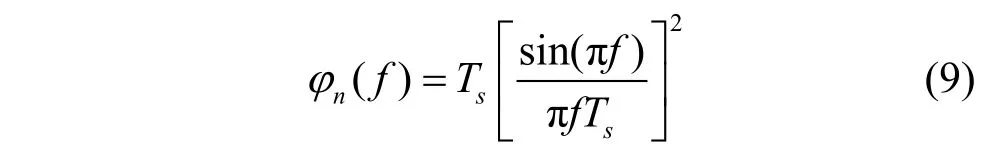
其中，Ts为抽样间隔。

1.2 引入接收SINR 的开/闭环功率控制策略

由式(3)和式(8)分析可知，认知异构蜂窝网络的用户接入信道会存在层间干扰和带外干扰问题。为有效降低系统的干扰，利用算法初始化发射端发射功率，利用算法对用户发射功率进行动态自适应调整[21]。基站通过调整用户参数下发功率控制命令给用户端，而用户接收到相应指令后通过上调/下调等方式对发射功率进行控制。引入开环功率控制和闭环功率控制的发射功率分别为

其中，Pmax为最大发送功率；α1和α2为路径补偿因子，本文取值为0.6 和0.7；PL 为路径损耗，定义如式(1)所示；ΔCMS为用户功率偏移量，与系统编码调制方式有关；P1为高层信令的功率基准值，其主要由两部分组成，P1=额定P1+用户P1，额定P1为小区特定参数，表示干扰或接收端SINR 设定的值，用户P1为终端特定参数，由终端位置确定，根据文献[18]中P1的动态范围为[-126 dBm,23 dBm]，本文取P1=-80 dBm；f(Δi)为闭环功率控制的反馈项，由Δi上调或下调功率。对于闭环功率控制策略，LTE 定义了累积式和绝对式为闭环功率的反馈因子，本文利用累积式对反馈进行调整，表示为

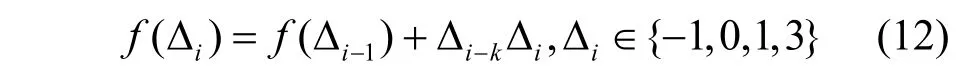
1.3 问题描述

由上述讨论，假设CFU 和MU 的信道资源和状态均已确定，在保证用户QoS 的情况下，以系统的最大能量效率（EE,energy efficiency）为优化目标。EE 的定义为

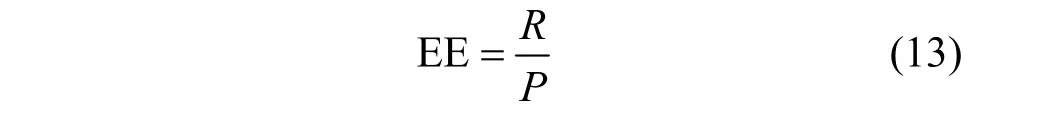
其中，R为用户传输速率，即吞吐量；P为发射功率。第s个CFBS 在第f个CFU 是否复用信道n的资源表示为ρs,f,n，若ρs,f,n=1，则表示接入信道，反之没有。

因此，根据上述模型可建立本文考虑用户QoS的目标函数及约束条件为

其中，P0为发射机电路设备功率损耗，Pmax为系统最大传输功率，Rmin为满足RT 用户的最小传输速率，为第n个信道上的干扰阈值。因此，式(14)为能量效率最大化的目标函数，式(15)为用户接入信道状态，式(16)表示一个信道最多供一个用户接入，式(17)为用户传输速率约束，式(18)为功率控制约束，式(19)为干扰约束，式(20)为SINR 阈值，超出该阈值则利用CLPC 进行上调/下调。

由式(14)～式(20)可以看出，本文为含约束优化的目标优化问题，考虑到网络用户接入间的分配，该优化问题属于非线性优化问题，为NP 完全问题。以往对NP 问题的资源分配往往采用穷举搜索求解，需要遍历所有可能的分配方案，求解时间复杂度较高。基于此，本文考虑用离散蜉蝣算法求解本文NP 非线性组合问题，能简单、快速地搜索到目标最优分配方案。

2 融合改进离散蜉蝣算法求解认知异构蜂窝网络资源分配问题

2.1 离散蜉蝣算法

蜉蝣算法求解资源分配问题时将蜉蝣群体位置映射为目标优化的可行解，即是否复用资源；将全局最优位置作为最优分配方案及函数适应度作为优化效果的判据。原始蜉蝣算法求解目标问题通常是连续的，而资源分配问题的求解结果需为离散的，因此先进行蜉蝣算法的离散化。对于连续型蜉蝣算法而言，雄性蜉蝣和雌性蜉蝣的速度和位置更新略有差异。现对蜉蝣算法的速度和位置更新进行叙述。

1) 雄性蜉蝣速度和位置更新

当雄性蜉蝣投放到有界区域时，群体之间会发生聚集行为，且按照一定的社会作用进行速度和位置的变化。雄性蜉蝣的速度更新式为

其中，为雄性蜉蝣i在j空间上第t+1次迭代的速度；a1和a2为2 个正吸引系数；Gj为第j维的全局最优位置；Pij为蜉蝣的局部最优位置；β为能见度系数，用于控制能见范围；d为舞蹈系数，且d=d0δt,d0为舞蹈系数初始值，t为迭代次数；g为惯性权重系数，r,δ均为取值为(0,1)的随机数；rp和rg分别为当前位置与Pij的笛卡儿距离和当前位置与Gj的笛卡儿距离。雄性蜉蝣的位置更新式为

其中，是雄性蜉蝣i的第t+1次迭代的速度，是蜉蝣i的第t次迭代的位置。

2) 雌性蜉蝣速度和位置更新

与雄性蜉蝣不同的是，雌性蜉蝣会靠近雄性蜉蝣交配繁殖。因此，雌性蜉蝣的速度和位置更新式分别为

其中，a3为雄性蜉蝣和雌性蜉蝣之间的吸引系数，β为能见度系数，r m为雄性蜉蝣和雄性蜉蝣的笛卡儿距离，fl=fl0δt为随机游走系数，r,δ为(0,1)的随机数，g为惯性权重系数。

3) 交配繁殖

蜉蝣的交配过程表示为交叉算子。首先从雄性蜉蝣中选择一个父本，雌性蜉蝣中选择一个母本，父本选择的方式与雄雌吸引的方式一致。采用优胜劣汰机制，将最优个体的雄性和雌性蜉蝣进行繁殖得到最优个体；依次类推，得到的2 个子代分别为

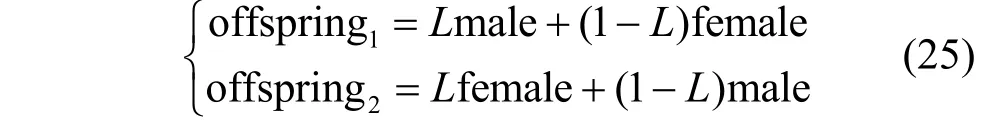
其中，L为服从高斯分布的随机数，取值范围为(-1,1)；male 为父本，female 为母本。

根据上述的速度和位置更新式可知，速度和位置均为连续变量，对于资源分配问题的求解，还需离散化更新方式，因此利用sigmoid 函数[22]将速度映射为(0,1)区间的值，然后根据式(26)和式(27)将速度离散为0 或1。

2.2 改进的离散蜉蝣算法

由于原始蜉蝣算法具有收敛精度低且求解速度慢等特点，应用于资源分配中也容易导致搜索滞慢等缺陷。本文针对这些缺陷进行改进，使改进离散蜉蝣算法具备更快的收敛精度及速度，使算法求解更快、更接近最优分配。

2.2.1 不完全Gamma 和Beta 函数自适应权重

惯性权重的引入可以使算法具有一定的先验指导作用，是继承算法先验信息的能力。在前期，为了具有方向性搜索，需根据历史搜索状态更快速地搜索到局部位置附近点。在后期，群体的大量聚集会因相似度过高和多样性缺失陷入局部最优，此时需要削减先验信息使种群后期自由探索，让群体根据社会认知部分进行信息交流合作，以此来提升后期算法搜索到全局最优的概率。引入不完全Gamma 函数[23]和Beta 分布函数[24]进行自适应动态调整权重g(t)，其定义为

其中，动态自适应权重和λ、ν、σ等参数有关，λ为控制Gamma 函数的随机变量，ν为偏移因子，b1和b2为服从Beta 函数的随机数。式(29)和式(30)分别为Gamma 函数和Beta 函数，它们存在转换关系，因此具备相互调整功能。式(31)中σ为非线性控制因子，起自适应作用，取值由相邻迭代间的适应度决定，前期取值较大是因为适应度下降具有差异，后期适应度取值变化较小，从而取较小的σ控制动态权重g。因此，引入Gamma 函数和Beta 函数，能自适应动态调整算法的搜索，有效提升算法的搜索性能。

2.2.2 融合黄金正弦策略

黄金正弦因子是根据传统0.618 黄金分割法提出的，现已有黄金正弦算法Gold-SA[25]。黄金正弦分割起源于单位圆内的参数优化问题的空间搜索，具有寻优精度良好、收敛能力快速、复杂度低等特点。黄金分割因子的实现可表示为

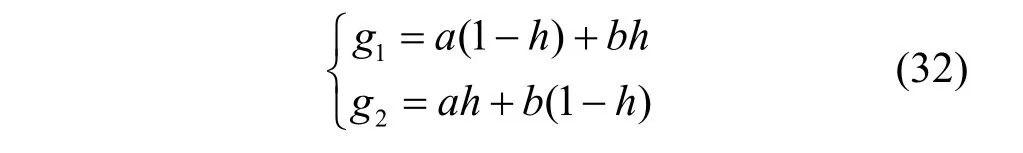
其中，a b、为黄金分割的初始值，h为黄金分割的比例系数，黄金正弦的参数推导见文献[25]。与MA 的子代交配繁殖相比，黄金分割完整对应于繁殖2 个子代的过程。Gold-SA 的位置更新式为

其中，为个体i在第t次迭代的局部最优位置，为个体i在第t次迭代的当前位置，r1和r2为随机数，取值分别为r1∈[0,2π]，r2∈[0,π]。将式(25)的变量分别映射到黄金正弦算法中，可得到2 个子代交配后的位置更新式为

将黄金正弦算法的思想融合到MA 中的交配繁殖阶段，有效避免算法交配繁殖的随机性，使算法在可行解空间得到更好的遍历。每经过一次迭代，根据黄金分割系数的调整使可行解空间渐渐缩小及向最优位置靠近，加快算法向最优位置靠近的能力，使算法能更有目的性、更快速地接近全局最优解，得到更精确的位置搜索，提升求解能力。

综上，本节对MA 进行改进，克服算法求解速度慢和收敛精度低等缺陷，使经过改进的MA 具备更好的搜索性能，为后续更好地求解资源分配问题提供新方案。

2.3 基于改进离散蜉蝣算法的资源分配策略

2.3.1 算法步骤及流程

本文利用改进的离散蜉蝣算法进行认知异构蜂窝网络资源分配问题的求解，其求解步骤如下。

步骤1种群初始化。初始化离散蜉蝣算法的位置向量，设置蜉蝣算法基本参数及种群大小为P。RT 和NRT 用户总数量为I，RT 用户赋予优先分配权值；随机产生离散可用的二进制信道分配矩阵和效益矩阵B={bi,n}I×N。当CFU 复用信道资源时所产生的干扰值为Ci,n，在可用带宽范围内的干扰矩阵为C={ci,j,n|ci,j,n=cj,i,n∈{0,1}}I×I×N。

步骤2逐个遍历所有存在干扰的用户。根据每个CFU到CFBS的实际距离和干扰距离判断是否会发生干扰，若存在干扰，则ci,j,n=cj,i,n=1；否则为0。同时，判断第i1行和第j1列的元素与第i2行和第j2列的元素是否为1，若都为1，则随机将其中一行的干扰元素置0。

步骤3以系统的能量效率作为目标适应度评价函数，按照初始化的效益矩阵B及分配矩阵A计算出最初适应度值，并记录局部最优位置和全局最优位置。

步骤4将所获得的初始能效优化值作为目标函数，并判断是否满足式(15)～式(17)的约束条件。若满足，将分配矩阵A、效益矩阵B和干扰矩阵C和目标函数传递到改进离散蜉蝣算法进行迭代求解。

步骤5判断算法是否满足迭代结束条件。若满足，则停止迭代，输出资源分配矩阵和最优能量效率；否则，返回继续执行步骤3。

步骤6算法求解完成。处理分配矩阵，并得出本次最优资源分配矩阵。

步骤7将最优资源分配矩阵逆映射为解向量，解向量顺序为信道顺序。映射过程见参考文献[26]。

为更清晰地了解算法的具体执行，图2 给出了改进的离散蜉蝣算法求解资源分配问题的算法流程。

图2 改进的离散蜉蝣算法求解资源分配问题的算法流程

为进一步探讨本文GSWBMA 对系统性能的影响，将系统公平性Fair 和最大网络效益函数进行对比分析。用户公平性评价和网络最大效益的计算式分别为

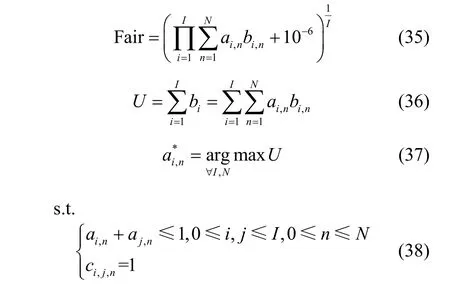
其中，Fair 为用户公平性计算；ai,n为用户i在信道n上的占用情况，占用信道资源则为1，否则为0；bi,n为用户i在信道n上的传输速率；ci,j,n为用户间的干扰，若存在干扰则为1，否则为0。

2.3.2 算法时间复杂度分析

算法时间复杂度是衡量一个算法好坏的基本指标。时间复杂度高会导致求解速度慢、效率低等，时间复杂度低会简化求解时间。设离散蜉蝣算法雌性数量为N1，雄性数量为N2，交配后的子代为N3，迭代次数为T。首先，设网络建立和目标函数初始化阶段所需的计算时间为t0，单次迭代雄性蜉蝣和雌性蜉蝣进行位置更新和速度更新的时间为t1和t2，复杂度分别为O(N1dt1)和O(N2dt2)，交配过程的更新时间为t3，引入黄金正弦，只是增加了O(1)的时间复杂度，可忽略不计。那么，算法求解需要利用目标函数和网络状态信息，结合初始化和迭代过程，求解的时间复杂度为O(t0+T((N1t1+N2t2)d+t0+1+t3))；对GSWBMA复杂度简化后，与MA 相比算法复杂度未明显提高，但算法的收敛能力得到明显改善。

3 实验仿真与分析

本节对改进离散蜉蝣算法的有效性进行验证并对认知异构蜂窝网络的资源分配问题进行求解。设本文二进制离散蜉蝣算法为BMA、融合改进的二进制离散蜉蝣算法为GSWBMA。另外，为充分对比算法和其他算法共同求解的有效性，还引入二进制粒子群优化（BPSO,binary particle swarm optimization）算法[17]、二进制遗传算法（BGA,binary genetic algorithm）[18]和二进制鲸鱼优化算法（BWOA,binary whale optimization algorithm）[27]。表1 为不同优化算法的参数设置。

表1 不同优化算法的参数设置

3.1 改进蜉蝣算法的有效性分析

为验证改进蜉蝣算法的有效性，本文利用CEC函数集的6 个函数进行分析，其函数信息如表2 所示。同时，表2 中的函数为无约束优化的连续函数，因此不需要离散化。设改进蜉蝣算法为GSWBMA，引入动态自适应权重策略的蜉蝣算法为WMA，黄金正弦因子的蜉蝣算法为GSMA。实验最大迭代次数为1 000，雄性蜉蝣和雌性蜉蝣种群个体数均为20，维度为30，独立重复30 次。

表2 6 个CEC 测试函数基本信息

表3 记录了MA 及改进算法在30 维搜索空间的最优值、平均值及标准差。从表3 中可看出，函数f1、f2和f4的改进算法可以达到理论值，与MA相比具有更好的收敛精度。改进算法中，黄金正弦策略的引入使算法在f1和f2函数中具有良好的搜索优势，直接达到理论值，且从平均值和标准差上看，算法求解的稳定性强；而MA 最优值和平均值的量级相差大，算法求解不稳定，收敛能力较差。f3函数特征复杂、寻求最优值难度大，但与MA 相比GSWBMA 依然能提升算法的收敛精度。对于函数f5，MA 的最优值达到了理论值，这是由算法的随机性造成的，其平均值和标准差整体而言收敛性不及改进算法，也进一步说明MA 求解过程的不稳定性造成的偶然误差。综上，算法的收敛性和精度在5 个函数中得以验证。

表3 CEC 测试函数的有效性对比

通过以上对比分析可知，改进算法在f1、f2和f4上均达到了理论值。为进一步验证算法收敛速度的快慢，得到理论值后，收敛快的算法具有更好的应用价值，图3(a)和图3(b)分别绘制了函数f1和f5的收敛曲线，从迭代过程判断算法的收敛性。由图3 可知，GSWBMA 的寻优速度最快，在应用中具备良好的应用价值。

图3 函数收敛性对比

3.2 不同算法优化对比分析

为验证本文提出的GSWBMA 求解认知异构蜂窝网络资源分配的潜能，在一定信道数量和用户条件下，通过实验对比算法求解的最大系统总效益和用户获得的公平性等。假设每个CFBS 服务CFU的数量不超过8，所有MU 和CFU 的QoS 需求相同；由于MU 享有接入优先权，MU 的发射功率设置比CFU 大。认知异构蜂窝网络系统参数设置如表4 所示。

表4 认知异构蜂窝网络系统参数设置

图4 为CFBS 数量为3、迭代次数为200、独立重复实验次数为5 的认知家庭网络的能量效率优化对比曲线。由图4 可知，能量效率收敛性最好的是GSWBMA，其次是BMA；除BMA 外，其他算法在大约20 次后就达到收敛效果，而BMA 需要160 次左右，由此也说明本文改进的GSWBMA 的寻优精度和收敛速度都得到很大提升。根据实验数据，GSWBMA 较BMA 而言，EE 算法求解的能量效率提升0.219 Mbit/(s·J)，而BGA 的收敛效果最差，经200 次迭代后的EE 为3.351 Mbit/(s·J)，与GSWBMA 的4.557 Mbit/(s·J)相比改进离散蜉蝣算法能提升1.206 Mbit/(s·J)。

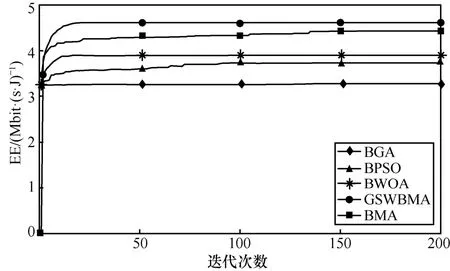
图4 CFBS=3 的能效优化收敛曲线

能量效率的对比收敛曲线引入了闭环功率控制策略，通过对发射机发射功率进行约束，可有效降低通信系统中的干扰。图5 绘制了CFBS=3 时采用2 种功率控制算法的累积分布函数（CDF,cumulative distribution function），在不同SINR 时满足RT 用户的最小传输速率的概率，以此验证引入闭环功率控制的降低系统干扰的有效性。

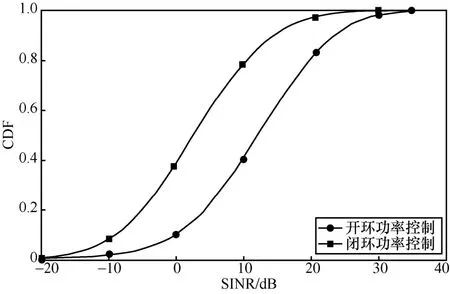
图5 不同SINR 的CDF 分布曲线

由图5 可知，随着SINR 的不断提升，能满足RT用户的传输需求的概率也在不断上升。当CDF 取值相同时，引入闭环功率控制策略只需更小的SINR 就能达到等概率的传输速率需求；当SINR 相同时，引入闭环功率控制策略能满足用户传输需求的概率更大。由此，通过引入自适应动态控制用户端发射功率能有效降低系统的干扰，提升用户QoS 需求。表5为不同算法求解用户接入信道的公平性和网络最大效益对比，目的是当用户获得较公平的资源接入和最大效益时，对比CFU 分配资源的公平性。

表5 不同算法求解用户接入信道的 公平性和网络最大效益对比

由表5 可知，GSWBMA 的公平性和最大系统效益均为最高，且与其他算法相比有更好的优势，即寻优的资源分配矩阵解的效果更好。公平性和网络最大效益越高，资源分配更加合理，且在最大化能效的基础上提升用户接入公平性能使网络容量得到有效提升，算法的遍历搜索更彻底，求解效果更好。公平性最差为BPSO 算法，为47.309 7；网络最大效益最差为BGA。由此可看出BPSO 和BGA对资源分配问题的求解很快就陷入局部最优、收敛能力低。因此BGA 和BPSO 不是最优算法。

3.3 不同CFBS 数量和不同干扰阈值下各算法优化性能对比

上述仿真实验为CFBS 数量和用户数量一定时的对比，但仅有单一对比实验不够充分。为进一步验证GSWBMA 求解认知异构蜂窝网络最优资源分配问题提升网络性能的可靠性，本节对比了不同CFBS 数量和不同干扰阈值下的性能。为了避免算法求解的随机性和偶然性，实验结果为独立重复10次取平均值。

图6 为不同CFBS 数量下的能量效率曲线，CFBS 数量从3 持续增加到24。由图6 可知，随着CFBS 数量的增加，系统的能量效率呈下降趋势，这是因为当MU 和CFU 的数量一定时，部署过多的CFBS 会出现能量损失、用户接入选择性较多、部分资源未利用的情况，导致能量效率降低。由于认知异构蜂窝网络考虑用户QoS，满足最大化用户传输速率需求，因此在具有充分的可接入资源情况下能选择较好的资源复用。由图6 可知，随着CFBS数量增加，本文GSWBMA 具有较好的能量效率，资源分配更加合理，同时更好地满足用户QoS 需求。

图6 不同CFBS 数量下的能量效率曲线

图7 为抛开EE 中用户发射功率及损耗情况下不同CFBS 数量下的RT 用户平均传输速率对比。由于RT 业务时间敏感性较强，因此需快速分配资源，具有较高的分配优先级。由图7 可知，随着CFBS数量增多，RT 用户的平均传输速率增大，当CFBS数量达到18 时，各算法求解的传输速率接近，这是因为随着CFBS 数量增加，用户选择接入的机会增大，各算法求解此类问题的难度变小，从而求解结果接近；当CFBS 数量较少时，GSWBMA 与其他算法相比有较好的RT 用户传输速率，由此证实了GSWBMA 在RT 用户下分配的优越性。从图7可以看出，RT 用户的平均传输速率明显大于最小传输速率需求（1 Mbit/s），所有RT 用户传输速率需求均得到保证。

图7 不同CFBS 数量下的RT 用户平均传输速率对比

系统中用户、基站部署的增减都会影响到层间干扰和带外干扰问题，为了对比不同干扰水平下不同算法的传输速率，图8 给出了不同干扰阈值下CFN 的平均传输速率曲线。随着干扰阈值门限的上升，CFN对宏蜂窝网络的干扰程度与干扰阈值门限呈正相关，每个系统的子信道获得的功率随之增大，因此CFN的传输速率会增加；而GSWBMA 在不同干扰阈值下传输速率具有显著优势，尽管干扰阈值门限增加，GSWBMA 求解CFN 的传输速率也有良好的效果。

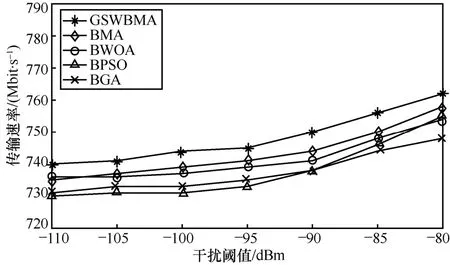
图8 不同干扰阈值下CFN 的平均传输速率曲线

图9为CFU接入CFBS对CFU间的公平性影响。当CFU 数量增加时，用户间的干扰冲突也会随之增加，网络负载变得严重，从而导致用户接入公平性降低。由图9 可知，随着CFU 数量增加，用户接入公平性会随之降低，当CFU 数量达到20 以上时，总信道数量为35，MU 和CFU 的总用户数量超过最大信道数量，资源分配优先满足授权的MU，其次是认知用户中的RT 用户，随后是其他业务用户，因此部分CFU 不能复用资源，从而用户接入公平性降低。当CFU 数量为20 时，GSWBMA 的公平性大小为31.020，其次是BMA 为27.681，GSWBMA 的公平性比BMA 的公平性高3.339；当CFU 为30 时，GSWBMA 的公平性为11.37，其次是BMA 为9.32，最差是BGA 为8.37。随着网络负载增加，CFU 竞争激烈，仅满足部分CFU 接入，因此GSWBMA 与其他算法相比求解CFU 依然具有较好的公平性。

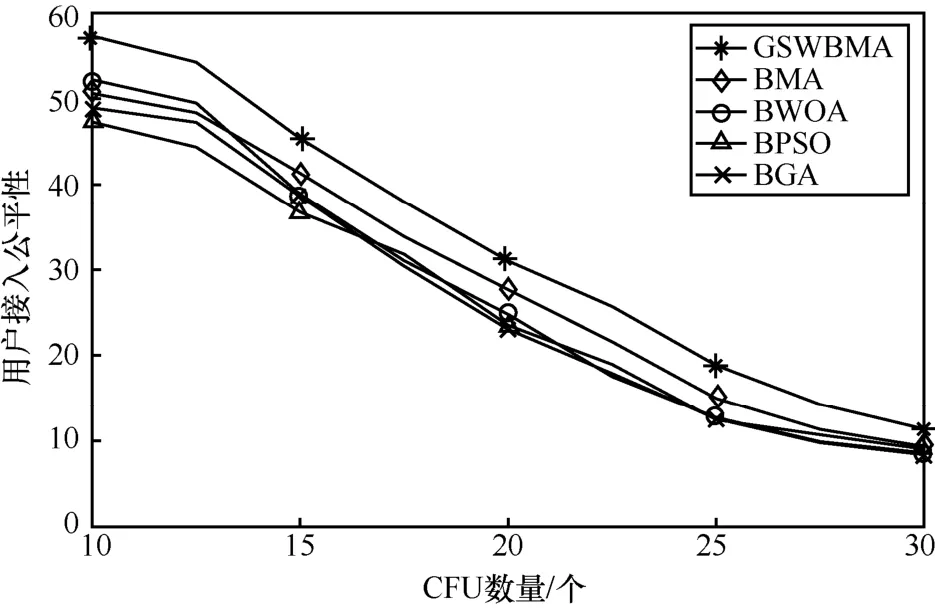
图9 CFU 接入CFBS 对CFU 间的公平性影响

4 结束语

本文主要分析了基于两层认知异构蜂窝网络的资源分配问题，提出了改进离散蜉蝣算法的资源分配策略。在认知异构蜂窝网络中，综合考虑用户的QoS需求、层间干扰和带外干扰等，同时为降低系统干扰引入闭环功率控制策略，使系统能够实时反馈调节发射功率，降低系统干扰，提升网络性能。针对蜉蝣算法求解精度低等缺陷，引入不完全Gamma 和Beta函数自适应动态惯性权重和黄金正弦策略，以此提升MA 的寻优效率和收敛性能，以及求解资源分配问题的有效性，并为求解资源分配算法复杂度进行简要分析。通过算法有效性对比实验，验证算法具有良好的寻优潜力；在保证用户QoS 需求下，从最大化能量效率、传输速率和不同CFBS 部署等视角验证GSWBMA 在认知异构蜂窝网络资源分配问题求解的优越性。同时，实验也表明较好的资源分配方案能有效提升认知异构蜂窝网络的性能。