三维圆柱型颗粒堆坍塌问题的全相态数值模拟1)
陈福振 李亚雄 史腾达 严红
(西北工业大学动力与能源学院,西安 710072)
(西北工业大学太仓长三角研究院,江苏太仓 215400)
引言
颗粒堆坍塌问题是自然界和工业工程中最为常见的一种物理现象,如仓库堆积物料突然塌方现象、砂粒输运过程中的倾翻现象、地球物理中的岩石崩塌、雪崩、海底塌方等等,给人类的生命和财产安全造成严重的影响.尽管这种现象无处不在,但即使是涉及颗粒介质的静态问题,例如确定静止沙堆底部中心的压力问题等,仍然存在一定的争议.而运动的颗粒介质则呈现出更加丰富和复杂的现象,如最为典型的颗粒介质在不同体积分数和载荷作用下会表现出类固体行为、类液体行为、类气体以及完全离散的惯性行为等[1-5].因此,建立可有效描述这些不同行为的颗粒介质运动宏观预测理论一直是物理学领域的一个重要目标,其中Science也将颗粒介质力学行为的通用理论模型定义为人类尚未解决的125 个科学难题之一.本文就主要针对颗粒堆坍塌过程中所表现出的复杂相态特性,建立一种描述颗粒介质全部相态的物理模型和数值模拟方法,为预测颗粒堆坍塌规律提供一条新的有效的途径.
在颗粒堆坍塌实验方面,Lube 等[6]研究了三维轴对称颗粒堆坍塌过程的三种流动状态,分析了不同高宽比下的运动规律.在此基础上又补充开展了二维不同材料下的坍塌过程实验[7].Lajeunesse 等[8-9]采用矩形通道和半圆形管道两种不同的装置,实验获得了二维和轴对称颗粒坍塌运动过程,特别是获得了颗粒堆内部流动结构.Roche 等[10]开展了细颗粒(约75 μm)和粗颗粒(约330 μm)情况下,最初与空气流化形成的轴对称颗粒堆释放产生重力颗粒流铺展的实验结果.Artoni 等[11]研究了湿颗粒堆的坍塌特性,旨在收集湿颗粒介质中的坍塌触发和休止现象的实验数据,获得了不同粒径、不同液体表面张力和不同液体量的玻璃微珠样品的最终沉积形态和铺展动力学过程.以上为典型的在水平表面上开展的颗粒堆坍塌实验.除此之外,文献[12-16]开展了在斜面上进行颗粒堆坍塌实验的工作.虽然实验可以获得颗粒堆坍塌过程典型时刻结果,但是费时费力,同时颗粒运动的细节无法全部获取,对于揭示颗粒运动的机理支撑度有限.因此,基于颗粒介质运动理论,采用数值模拟的方法对颗粒堆坍塌过程进行深入研究,对于全面掌握颗粒堆坍塌运动规律,预测颗粒介质运动的不同现象具有重要意义.
在颗粒堆坍塌数值模拟方面,主要包括两大类方法,一类是以离散元(DEM)为代表的颗粒轨道追踪方法,通过计算作用在每个离散单元上的作用力给出其单独运动的轨迹.文献[17-19]采用DEM 方法对平面上颗粒堆的坍塌过程进行了数值模拟.孙其诚和王光谦[20]对重力作用下12000 个球心共面的二维等径颗粒静态堆积进行了离散动力学模拟,从力链角度揭示颗粒静态和动态性质.成浩等[21]基于DEM 方法对松散体滑动堆积特性及影响因素进行了分析.Zhang 等[22]采用DEM 方法对三维颗粒堆坍塌过程进行了数值模拟,研究了颗粒堆厚度对坍塌过程的影响.DEM 方法对于揭示颗粒介质的运动机理、拟合获得颗粒介质的宏观统计特征、小规模的工程应用非常有效,但是该方法的计算消耗对于模拟工业系统中存在较大数量的颗粒来说往往遥不可及;该方法所使用的参数和模型是单颗粒层次的,往往与可开展的宏观实验不匹配;计算的时间步长与颗粒的硬度息息相关,往往很受限制.虽然有学者[23-24]开发了DEM 的粗粒化处理技术,但存在着条件苛刻、放大不足、颗粒变硬需要进一步降低时间步长而增大计算时长等问题.
另一类是基于宏观连续介质力学的数值模拟方法,如求解颗粒弹塑性本构模型的有限元方法(finite element method,FEM)[25]和有限体积方法(finite volume method,FVM)[26],求解基于流变学的黏塑性本构模型的FEM[27-29]和FVM[30-32]等,此类方法的特点是基于网格离散求解数理模型,已成功用于颗粒堆坍塌、剪切造粒、化工流化床、颗粒管道输送等问题中,但此类方法存在的最大问题是必须依赖网格求解带来的缺陷,如有限元在计算类固态和小变形的类液态时是合理的,但对于颗粒介质宏观大变形问题或者类气态问题往往会出现网格的扭曲和缠绕,计算终止;而采用有限体积法解决颗粒类气态问题和类液态问题较为合适,但类固态本构模型无法求解,同时该方法无法获得颗粒的运动轨迹,易产生伪扩散,不易加入颗粒蒸发、燃烧等物理化学模型.
为了克服网格方法在求解颗粒宏观连续介质力学模型上的不足,有学者尝试采用粒子类方法进行模拟,如文献[33-38]均采用物质点法(material point method,MPM)根据土壤的连续介质力学模型计算了类土体的颗粒介质运动问题.此类方法一方面较难处理颗粒的类气态问题,甚至是体积分数更小的惯性态,这时需要将气相应力强制置零[38],或者引入其他模型来处理干燥颗粒材料的离散运动;另一方面物质点法必须使用背景网格,依赖于背景网格求解动量方程,不可避免地存在网格重分、大范围布置背景网格、网格与物质点之间需要不断反复插值的问题.
光滑粒子流体动力学方法(smoothed particle hydrodynamics,SPH)[39-40]作为另外一种完全拉格朗日粒子方法,对离散颗粒进行模拟表征具有很大优势.SPH 不仅适合于模拟处于类固态和类液态的颗粒相体积分数几乎保持恒定的问题[41-46],同时对于类气态问题也非常适合模拟.Chen 等[47-51]前期就在传统SPH 方法的基础上建立了SPH 粒子与类气态离散颗粒间的一一对应关系,将SPH 改造成适于分散性颗粒相求解的光滑离散颗粒流体动力学方法(smoothed discrete particle hydrodynamics,SDPH),耦合FVM 求解连续气体相,成功应用于化工流化床[48]、风沙跃移[49]、气-粒传热[50]、空气燃料抛洒[51]等领域中,解决了气流载体作用下离散颗粒的类气态数值模拟问题.Chen 和Yan[52-53]近些年尝试将SDPH 方法应用于颗粒其他相态的数值模拟,取得了一定的进展.
本文即在此基础上,进一步探索建立颗粒介质的全部相态物理模型.从颗粒表现出不同相态的物理机理出发,将描述颗粒介质的弹塑性理论、黏塑性理论、颗粒动理学理论以及单颗粒输运理论有效结合起来,通过确定不同相态之间的过渡关系和转化准则,建立描述颗粒介质经历全部相态的耦合模型理论,不同相态之间不仅可以共存,同时可以正向和反向转化.然后,采用SDPH 方法模拟类固态、类液态和类气态,同时耦合DEM 模拟颗粒离散惯性运动状态,建立求解颗粒介质全部相态的数值模拟新方法.新方法针对不同的相态采用不同的与之相匹配的粒子方法,既保证了对各个相态的准确描述和动态再现,又降低了计算量.最后,采用新的理论模型和数值方法,对不同长径比条件下的三维圆柱型颗粒堆坍塌问题进行了数值模拟,一方面验证了模型和方法的准确性和适用性,另一方面探明了影响颗粒堆坍塌特性的因素和机理,为颗粒介质运动问题的解决提供理论和数据支撑.
1 颗粒介质全相态物理模型
颗粒介质作为一种由介观离散颗粒组成的宏观无定型态物质,根据颗粒的体积分数不同和载荷作用条件不同会表现出一些不同的行为特征,例如颗粒体在堆积状态时,整体表现出类似固体结构的行为,运动非常缓慢,在屈服的过程中会形成剪切带,应力状态也表现出率无关状态,这种状态为颗粒介质的类固态,称之为颗粒固相;当颗粒堆积过程中承受的等效剪应力与等效体应力的比值超过一定阈值时,颗粒介质发生塑性流动,产生类似于液体之间的黏性剪切作用效果,这种状态为颗粒介质的类液态,称之为颗粒液相;当颗粒之间运动的速度梯度继续加大,颗粒体积分数减小,不再等价于不可压缩状态时,颗粒与颗粒之间的相互作用力也不再遵循多颗粒接触假设,而主要以频繁的二体碰撞为主,碰撞速度相互独立,应力表现为剪切率的二次函数,这时的颗粒介质表现出类似气体运动的行为,这种状态为颗粒介质的类气态,称之为颗粒气相.
以上是目前国内外对于颗粒介质存在的三种相态的描述,作者通过分析发现当颗粒的体积分数继续减小,颗粒间的二体碰撞假设也不再满足,颗粒间碰撞的概率已经非常微小,颗粒主要以受到的体力作用和外部流场作用为主,这时从相对尺度上来说颗粒属于介观尺度范围,不再遵循拟流体的连续介质力学定律,因此不适用于以上三种状态描述,将这种状态称为离散惯性相,遵循质点运动定律.由此,颗粒介质从浓密到稀疏、从连续到离散、体积分数从1 至0 的全部相态可全覆盖,如图1 所示.
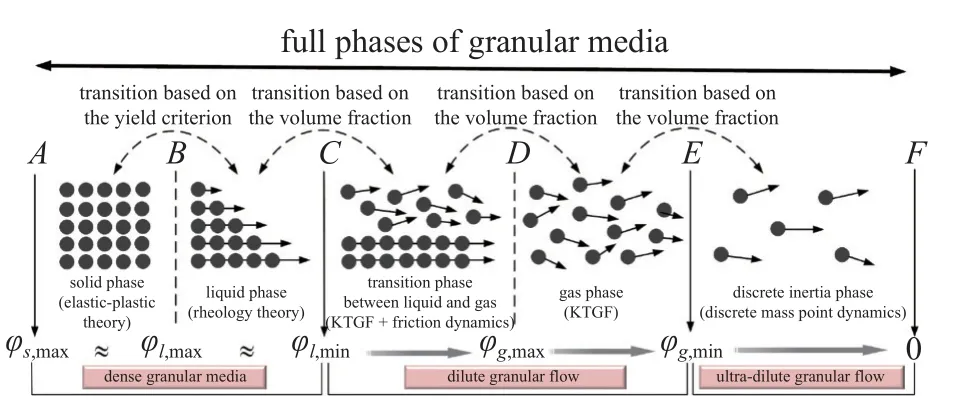
图1 颗粒介质全相态定义及物理模型示意图Fig.1 Definition and diagram of the physical model of all phases of granular media
本文在建立颗粒介质全相态理论之前,根据颗粒稀疏程度的不同将全相态划分为三个区域,将颗粒固相和液相区域统称为浓密颗粒介质区(φl,min≤φp≤φs,max,φp为颗粒体积分数,φs,max为颗粒固相最大体积分数,φl,min为颗粒液相最小体积分数,通常 φl,min≈φs,max);将颗粒液相和气相之间的过渡相和气相区域称之为稀疏颗粒介质区(φg,min≤φp≤φl,min);将离散惯性相区域称之为超稀疏颗粒介质区(φp<φg,min).划分区域的目的是分区域建模,使复杂的多相态建模能够实现一定程度的简化.建立颗粒介质的全部相态本构理论就需要根据其所处的不同相态区域进行建模,同时建立不同相态之间的转变原则:
(1) 对于浓密颗粒介质区域状态采用弹-黏-塑性本构理论描述,具体针对浓密颗粒介质固相采用弹塑性理论描述,对于浓密颗粒介质液相采用流变学理论描述;
(2)对于稀疏颗粒介质区域状态采用颗粒动理学理论和摩擦动力学理论描述,具体针对稀疏颗粒介质的液气过渡相采用颗粒动理学和摩擦动力学相结合的方式描述,对于稀疏颗粒介质气相采用颗粒动理学描述;
(3)对于超稀疏颗粒介质区域状态采用质点动力学理论描述,具体就是指针对超稀疏颗粒介质的惯性相采用质点动力学理论进行描述.
下面就分别介绍这些不同的理论,以及这些理论之间的转变原则.
1.1 描述浓密颗粒介质运动状态的弹-黏-塑性本构模型(φl,min ≤φp ≤φs,max )
对于浓密颗粒介质来说,首先介绍其运动控制方程,包括质量守恒方程和动量守恒方程两个,如下
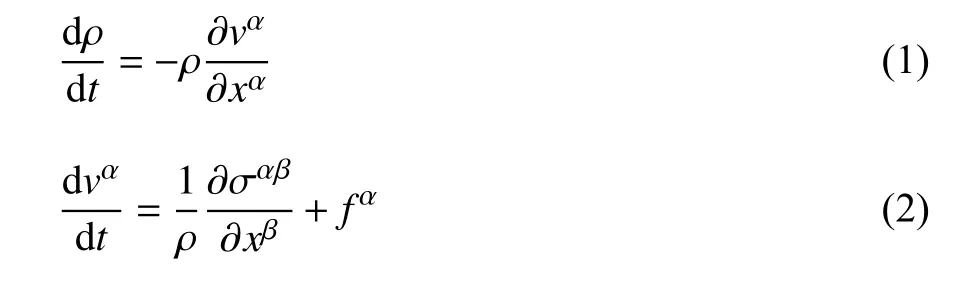
本文应用了爱因斯坦求和约定的指数表示法,α和 β 分别表示笛卡尔坐标系下的1,2 和3 三个分量,ρ 为材料的密度,v为速度,σαβ为材料的全应力张量分量,通常由两部分组成:各向同性静水压力p和应力偏张量s
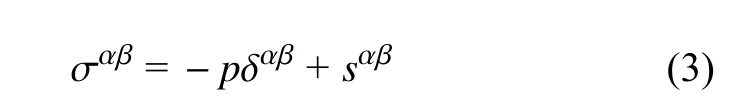
式中,δαβ是克罗内克函数,当α=β时δαβ=1,当α≠β时δαβ=0.静水压力p直接采用本构方程中的应力计算得到

全应力张量的具体形式将根据其所处的状态不同而发生改变,具体见以下章节介绍.fα为其他外力,如本文中所需要考虑的重力.d/dt为全导数.
有效耦合现有的弹塑性理论和基于流变学的黏塑性理论,获得基于稠密颗粒运动弹-黏-塑性理论的颗粒固液相计算模型[52].假设准静态和流动状态之间的屈服准则用Drucker-Prager 屈服准则表示,则可以建立从完全弹性到弹性-微黏塑性再到完全弹性-黏塑性的过渡过程,如图2 所示.

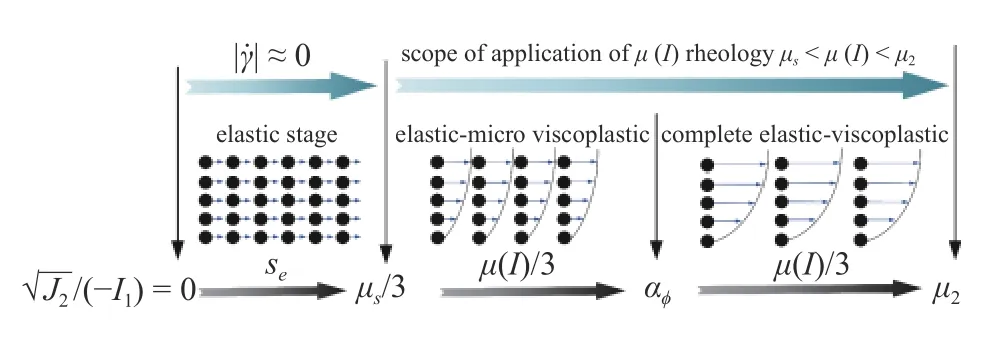
图2 完全弹性到弹性-微小黏塑性再到完全弹性-黏塑性的过渡过程Fig.2 The transition from complete elastic to elastic-micro viscoplastic and then to complete elastic-viscoplastic

1.1.1 完全弹性下的颗粒介质应力-应变关系

1.1.2 弹性-微小黏塑性状态下的颗粒介质应力-应变关系
随着颗粒受力的增加,变形逐渐增大.弹性引起的剪应力逐渐增大,首先达到.此时,根据颗粒流变学理论,颗粒介质开始流动,和 µ(I)逐渐增加.虽然发生了流动,但流动速度非常小,尚未达到塑性屈服状态.在此阶段,只有剪应力逐渐增大.
弹性-微小黏塑性状态下颗粒介质的法向应力仍按线弹性本构模型计算,如式(5),剪应力按流变学模型计算,即


1.1.3 弹性-完全黏塑性状态下的颗粒介质应力-应变关系

以及其中的塑性乘子变化率公式

1.2 描述稀疏颗粒介质区域的颗粒动理学理论和摩擦动力学理论(φg,min ≤φp<φl,min )
1.2.1 描述颗粒气相的动理学理论(KTGF)
对于稀疏颗粒流区域中的颗粒气相,采用颗粒动理学理论(简称KTGF)[54-55]进行描述,一共包括质量守恒、动量守恒、拟温度守恒等三个方程,质量守恒方程和动量守恒方程如式(1)和式(2),拟温度守恒方程式为颗粒动理学理论所特有,如下

式中,ds为颗粒的直径,ess为颗粒之间的碰撞恢复系数.g0为颗粒的径向恢复系数
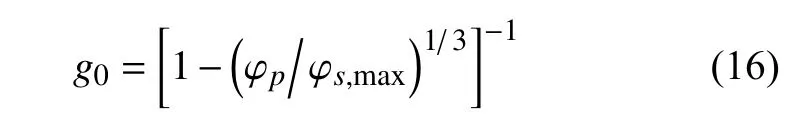
式中,φs,max为颗粒介质可达到的最大体积分数值.
1.2.2 描述颗粒气相-液相过渡区的摩擦动力学理论
摩擦动力学主要用来描述处于长程接触以及存在不可忽略的摩擦应力的颗粒.一些学者研究表明,摩擦动力学可以用于体积分数较高的颗粒[56-57].在稠密颗粒流和稀疏颗粒流之间,必然存在一个从长程接触到瞬态碰撞接触的过渡阶段.这里,摩擦动力学被用来弥补颗粒气相和液相之间存在的过渡缺陷问题.Johnson 等[58-59]提出的半经验模型用来计算由摩擦引起的法向应力,如下所示
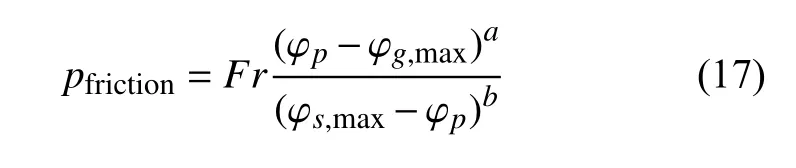
式中,Fr,a和b是材料的经验常数.摩擦黏度的计算最早由Schaeffer[60]在研究筒仓颗粒物料在重力作用下从锥形出口流动的过程中,假定服从理想刚塑性本构理论,获得了摩擦剪应力与正应力之间存在以下关系
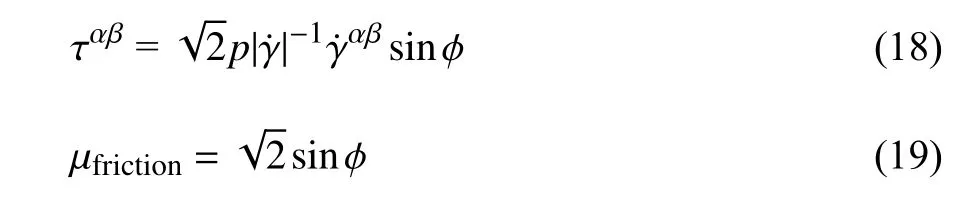
式中,ϕ 为内摩擦角.通过分析可知[53,59],摩擦动力学可以被认为是 µ(I) 流变学[61-62]在惯性数或者说剪切应变率无限大时的极限情况.
1.3 描述超稀疏颗粒流区域的质点动力学理论(φp<φg,min )
离散质点动力学是指针对具有一定质量但几何尺寸大小可以忽略的物体,采用牛顿运动定律进行描述的动力学过程
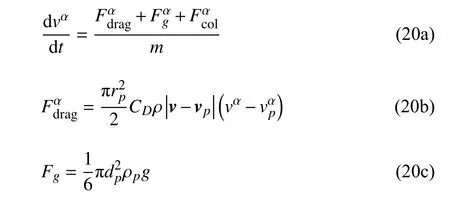
式中,右端项Fdrag为颗粒所受到的曳力.Fcol为颗粒之间的碰撞作用力,Fg为重力.本文重点是考虑颗粒间的碰撞相互作用力(见第3 节).
1.4 浓密颗粒流与稀疏颗粒流两个状态之间的转变原则
KTGF 结合摩擦动力学模型[56-57]用于计算颗粒液相和气相之间的转换.一些学者通过研究发现,摩擦动力学可以用于具有较高体积分数的颗粒,但当体积分数增加到某个值时存在不确定性.然而,将摩擦动力学与弹-黏-塑性模型相结合可以克服这一缺点.在转变过渡的界面处应力应保持守恒,弹性-黏塑性模型计算的法向应力和剪应力应与摩擦动力学计算所得的法向应力和剪应力相同.颗粒应力计算公式表示如下

式中,pEVP和 µEVP分别为采用弹-黏-塑性本构模型计算获得的正应力和剪应力,pKTGF和pfriction分别是颗粒压力pp中的动理学部分和摩擦部分,µKTGF和µfriction分别是颗粒剪切黏度 µp的动理学部分和摩擦部分.φg,max是摩擦应力开始逐渐增加时的颗粒体积分数.小于 φg,max值时,通过已知资料发现未观察到颗粒间的摩擦行为,因此假设,当均匀分布的粒子不再接触时,摩擦相互作用不再发生,主要由碰撞相互作用产生相互间的应力.
颗粒液相和气相之间的过渡如图3 所示.从颗粒液相和颗粒气相之间的过渡相开始,颗粒拟温度从零开始升高,表明颗粒之间的碰撞逐渐加剧.从过渡相到气相转变的界面上,颗粒之间的摩擦完全消失,转变为完全二体碰撞.从上述计算公式可以看出,用这种方法建立的过渡态可以有效地连接液相和气相,实现平稳过渡,符合物理定律.

图3 浓密颗粒流与稀疏颗粒流之间的过渡转化Fig.3 Transition between dense granular flow and dilute granular flow
1.5 稀疏颗粒流与超稀疏颗粒流两个状态之间的转变原则
对于颗粒体积分数小到一定数值后(φg,min),颗粒的宏观流动特征时间尺度明显小于微观碰撞特征时间尺度,对颗粒类气态的宏观连续描述不再成立,这时转化为颗粒质点进行追踪.由于在颗粒气相计算的过程中,进行了宏观拟流体假设,一个单元表征了在空间该位置处颗粒的统计平均信息,如颗粒的有效密度、颗粒的均值粒径、颗粒的均值速度等,这时在转化的过程中需要保证转化的质量、动量和能量的守恒.后面的章节中会介绍对于稀疏颗粒流采用的是拉格朗日粒子方法SDPH 进行离散求解,而超稀疏颗粒流的离散质点动力学也是采用粒子法DEM 进行模拟,因此转化的过程较为自然,可以保证物理量的守恒,同时为了更加贴近实际,还可以结合粒子分裂算法,使两者在空间位置上也对应起来.具体粒子间的转化方法见3.3 节.
2 颗粒介质全相态数值模拟方法
第2 节阐述了颗粒介质全相态理论,要对颗粒介质全相态进行数值模拟除了理论模型之外,还需要引入合适的数值模拟方法对模型进行离散求解.本文对于颗粒介质全相态中的类固态、类液态和类气态三种状态采用SDPH 方法进行模拟,因为这三种状态的本构模型均是基于宏观连续介质力学所建立的,与SDPH 的理论基础一致.当散体颗粒分散到一定程度即颗粒相的体积分数小到一定程度时,采用2.3 节的离散颗粒动力学进行描述,引入描述单一颗粒行为的离散单元法进行计算.
2.1 基于颗粒连续介质力学的光滑离散颗粒流体动力学方法
为明确SPH 粒子与颗粒之间的对应关系,Chen 等[47-51]前期已经从颗粒动理学角度出发,将颗粒相视为拟流体,拟流体区域采用SPH 方法离散求解,同时将传统SPH 方法改造成了适用于离散颗粒相求解的SDPH 方法,本文在此基础上继续拓展SDPH 方法的应用范围,对于颗粒固相和液相同样采用SDPH 离散阐述,与颗粒气相的SDPH 描述保持一致.
2.1.1 光滑离散颗粒流体动力学方法
在SDPH 方法中,实际颗粒的质量、速度、压力、位置、粒径分布、体积分数等均在计算粒子上有体现.同时,颗粒气相的拟温度值也作为计算粒子的一个参量.计算粒子与实际颗粒之间的参量对应关系如下

其中,p为颗粒下标,φp为颗粒体积分数,ρp为颗粒实际密度.颗粒的有效密度可进一步推导获得
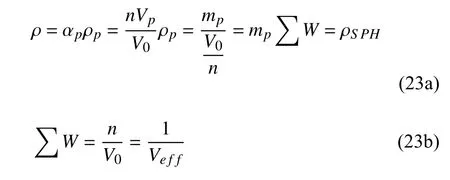
式中,n为空间内真实颗粒的总数目,Vp为每个实际颗粒所占据的空间体积,mp为每个实际颗粒的质量,V0表征了所有实际颗粒占据的空间总体积.式(23)表示计算粒子的密度等于真实颗粒的有效密度.单个计算粒子的质量和体积表征了空间中某些真实颗粒的总质量和体积.由每个计算粒子表示的真实颗粒数通过每个计算粒子的质量与每个真实颗粒的质量之比获得.计算粒子的速度、压力和拟温度取真实颗粒群相应参数的平均值.
从以上对应关系可以看出,当使用SDPH 方法进行计算时,每个计算粒子可以代表一定数量的真实颗粒群,计算粒子的数量可以根据计算精度的要求确定.对于某些精度要求不太严格的问题,计算量将大大减少,计算效率将显著提高.
2.1.2 颗粒固相和液相的SDPH 离散公式
在SPH 方法中,流体域被一系列粒子离散和求解.函数f(r) 及其空间导数 ∇ ·f(r) 在粒子i处的估计值为
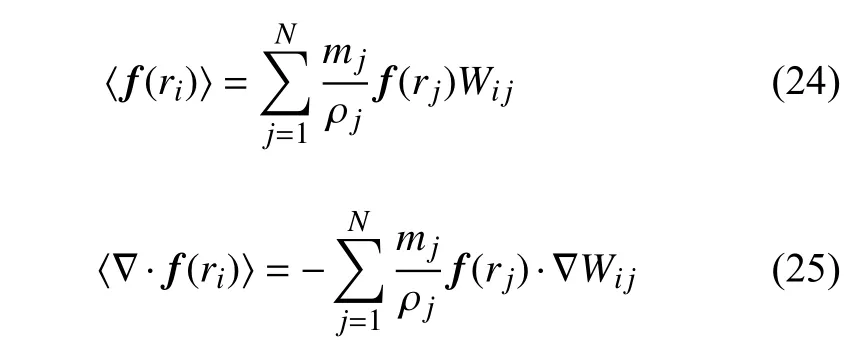
其中,m,ρ,r分别为物质的质量、密度和空间位置矢量,为光滑函数或核函数,本文采用三次样条核函数,h为光滑函数W的影响域或支持域的长度.
式(1)和式(2)中颗粒固相和液相的质量和动量守恒方程采用SDPH 方法离散,如下所示

其中,总应力张量 σαβ同样采用SDPH 离散,得到

为了满足零阶和一阶一致性条件,本文采用了一种基于核及其梯度正规化的SPH 方法的修正形式.核近似的修正形式:为了实现C0一致性,函数f(xi)的修正核近似为[63]
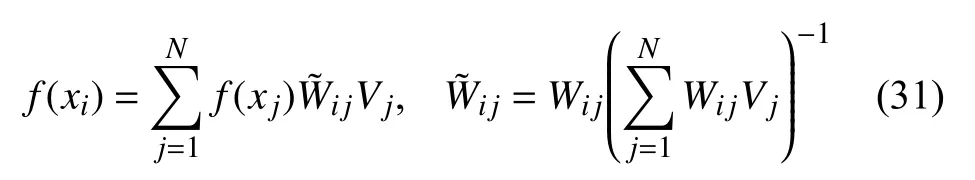
为了满足动量守恒和C1一致性,本文采用混合核和梯度修正公式[64],这种混合校正是一种改进核梯度的梯度校正和内核修正的组合,它改变了内核本身.梯度修正保证了角动量守恒,并且在内力与密度方程变化一致的情况下,精确计算了线性场的梯度,公式如下


2.1.3 颗粒气相的SDPH 离散公式
采用SDPH 方法对稀颗粒气相的拟温度守恒方程(11)进行离散,得到
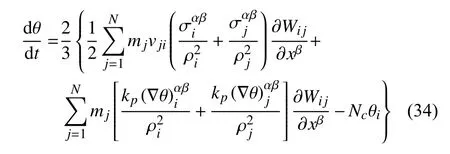
颗粒拟温度梯度 ∇ θ 采用SDPH 离散获得

不同于颗粒固相和液相,颗粒气相的拟温度变化率 d θ 需要额外进行计算.然后,采用式(33a)获得新的时刻的颗粒拟温度值 θ .
2.1.4 基于SDPH 方法的浓密颗粒介质与稀疏颗粒介质相态转变
采用SDPH 方法不论是求解浓密颗粒相还是稀疏颗粒相,计算粒子与实际颗粒之间的对应关系不会发生改变,只不过在求解的本构模型上存在不同.决定颗粒介质是处于浓密态还是稀疏态的参数是体积分数,体积分数的计算公式为.图4 展示了转变策略.如果计算粒子M的体积分数 φp大于φl,min,它表示该粒子正处于颗粒固相和液相.当 φp降低至小于 φl,min,它表示颗粒已经转变为稀疏颗粒状态或颗粒气相.将变换后的计算粒子标记为N.粒子M和N之间的变量关系如图4 所示.
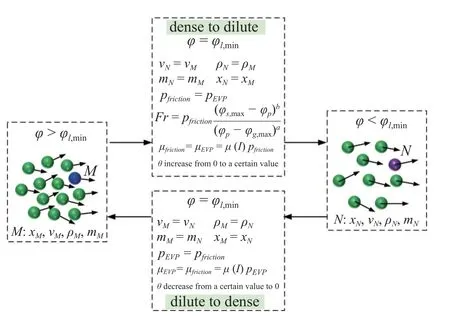
图4 基于SDPH 方法的浓密颗粒介质与稀疏颗粒介质相态转变Fig.4 Phase transition between dense granular media and dilute granular media based on SDPH method
首先要保持粒子的物性参量均不变,包括粒子的位置、速度、密度、能量等,主要区别在粒子间相互作用力上.由于浓密颗粒流的正应力采用弹性定律计算,剪应力采用弹性剪应力与塑性剪应力加和的方式计算,在向稀疏颗粒介质算法转变时,这两个作用力也应该保持不变,即由浓密颗粒介质计算的弹性正应力转化为稀疏颗粒介质的摩擦正应力,见式(17),由式(17)反向计算求得Fr作为不变量,而后根据体积分数 φp的变化更新由摩擦产生正应力的值;对于摩擦剪应力则继续采用 µ (I) 流变学剪应力公式计算 τ=µ(I)p|γ|/γ,只不过这时的p开始由式(17)计算;对于由长时接触产生的弹性剪应力则置零;以上是对于SDPH 采用摩擦动力学在过渡区产生的正应力与剪应力的数值计算,保证了转化的动量的守恒;同时从转化开始,拟温度的值由零开始计算,从而由碰撞产生的正应力和剪应力逐渐增大,直到过渡区全部转化为颗粒动理学模型计算.
同样地,对于颗粒从稀疏态转化为浓密态时,粒子变量值应该保持不变,包括粒子的密度、速度、能量、坐标等.两个状态的粒子存在的差别主要在内力的计算上.从稀疏态到浓密态过程中,颗粒的拟温度值逐渐降低,颗粒间的碰撞频次也逐渐降低,而由摩擦作用产生的正应力和剪切力数值则逐渐增加.在转化的界面上,由摩擦作用产生的正应力和剪切力与颗粒液相计算的正应力和剪切力相同.在转化为浓密颗粒态之后,颗粒间的塑性剪切力逐渐降低,弹性剪切力逐渐增加,颗粒速度逐渐降低,体积分数逐渐增加,按照塑性流动法则计算颗粒介质材料的卸载过程,直至恢复到静止状态.
2.1.5 基于SDPH 方法的浓密颗粒介质与稀疏颗粒介质间相互作用
当在空间中存在处于浓密状态的颗粒与处于稀疏状态颗粒共存时,两种相态的颗粒之间将有机会产生相互作用.图5 显示了SDPH 法中浓密介质和稀疏介质之间的相互作用.因为SDPH 粒子之间的相互作用与否取决于临近粒子搜索,当被搜索粒子位于搜索粒子的支持域时,被搜索粒子将对搜索粒子产生相互作用.假定处于稀疏状态的粒子为搜索粒子,处于浓密状态的粒子为被搜索粒子同时位于搜索粒子的支持域内时,两者产生类似于二体碰撞的应力,处于浓密状态的粒子对处于稀疏状态的粒子有力的贡献;当处于浓密状态的粒子为主粒子,处于稀疏状态的粒子为被搜索粒子同时位于搜索粒子的支持域内时,由于浓密颗粒之间的计算依赖于咬合接触,而稀疏颗粒与浓密颗粒之间的距离超出了咬合接触的范围,因此处于稀疏状态的粒子对浓密状态的粒子之间不产生内力作用,而转化为一种外力施加于动量方程右端项.

图5 基于SDPH 方法的浓密颗粒介质与稀疏颗粒介质间相互作用Fig.5 Interaction between dense granular media and dilute granular media based on SDPH method
2.2 基于颗粒质点颗粒动力学的离散单元法
采用DEM 对方程(20)中描述超稀颗粒流的微分方程进行离散,并给出以下方程

2.3 SDPH 与DEM 之间算法的耦合
2.3.1 SDPH 与DEM 之间算法的转化
在稀疏颗粒流SDPH 粒子的体积分数降到一定阈值后(φg,min)时,其不再遵循二体碰撞假设的颗粒动理学模型,因此将SDPH 粒子转化为DEM 粒子进行计算.图6 显示了SDPH 和DEM 之间算法的转化方案.

图6 SDPH 和DEM 算法之间的转化方案Fig.6 Conversion between SDPH and DEM
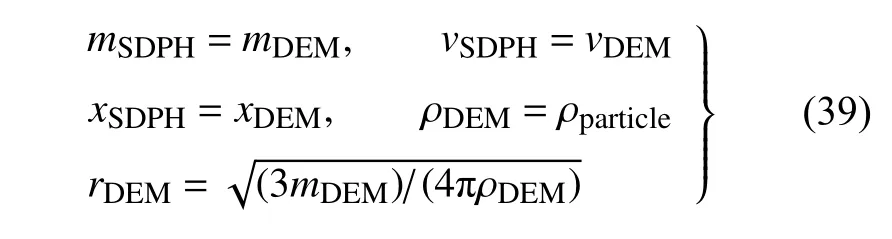
转化策略是,将一个SDPH 粒子转化为一个DEM 颗粒,SDPH 粒子的质量、速度、刚度、位置等参数与转化后的DEM 的粒子相同,DEM 粒子的密度为实际表征的颗粒的密度,因此根据DEM 粒子的质量和密度便可计算出DEM 在转化后的粒径大小,即与每个SDPH 粒子表征具有一定分布的颗粒群一样,采用该方法转化之后的DEM 粒子也是代表了一个颗粒群,代表的颗粒群的属性和参量与SDPH 粒子相同.存在的不同是,DEM 粒子中的颗粒体积分数为1,DEM 粒子的密度只有一个值即真实颗粒的密度.因此,与SDPH 粒子相比,DEM 粒子的尺寸明显小于SDPH 粒子的尺寸.可以看出,该处的DEM 粒子表征了具有相同粒径分布的颗粒群,等于是粗粒度的DEM 算法,采用文献中的算法计算[24].
2.3.2 SDPH 粒子与DEM 颗粒之间作用力传递
假如在计算颗粒介质过程中,空间中既有SDPH 粒子,又有DEM 粒子,当他们之间处于相互接触的状态时,需要计算他们之间的接触作用力.采用DEM 粒子之前的接触力计算方法进行计算.因此,需要将处于接触状态的SDPH 粒子转化为DEM 虚粒子进行计算(等效两个DEM 粒子接触计算).图7 展示了SDPH 粒子与DEM 颗粒之间的接触力计算规则.SDPH 粒子与DEM 颗粒之间相互作用力包括接触力Fc,ij=Fcn,i j+Fct,ij和法向接触阻尼力Fd,ij=Fdn,ij+Fdt,i j
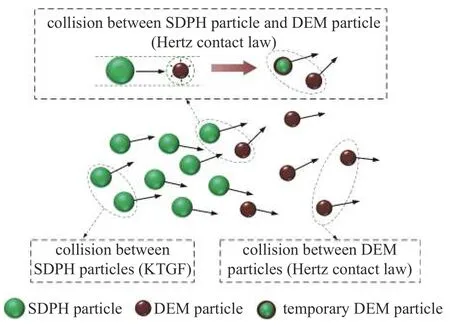
图7 SDPH 粒子与DEM 颗粒之间的相互作用Fig.7 Interaction between SDPH particle and DEM particle
考虑DEM 粒子对SDPH 粒子作用的SDPH 方法动量方程为
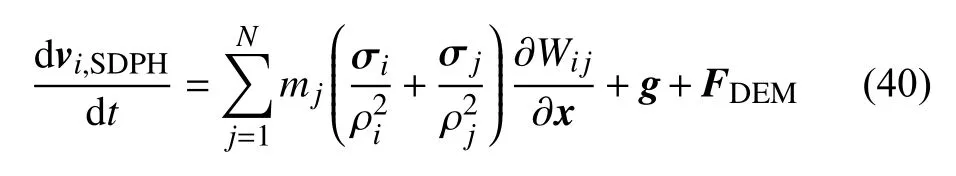
考虑SDPH 粒子对DEM 粒子作用的DEM 方法的动量方程
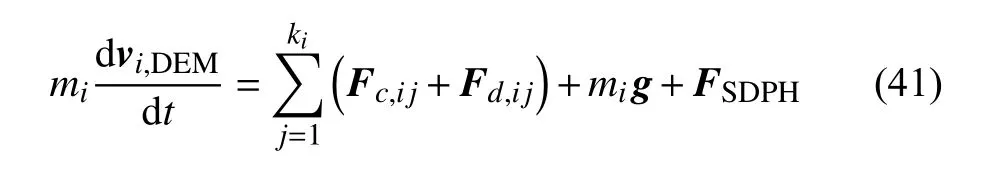
式中,FDEM为DEM 粒子作用于SDPH 粒子上的作用力矢量,FSDPH为DEM 粒子作用于SDPH 粒子上的作用力矢量.
2.4 边界条件
SDPH 和DEM 粒子与固壁边界之间的作用力分为法向边界力fn和切向边界力fτ,如图8 所示.

图8 SDPH 和DEM 粒子边界力施加方法Fig.8 Boundary force on SDPH and DEM particles
本文采用罚函数方法[67]计算SDPH 粒子与固壁边界之间的法向接触力,同时,为了保持算法的鲁棒性和参数选择的方便性,对罚参数进行了改进以保证法向力与SDPH 粒子到边界的距离成反比
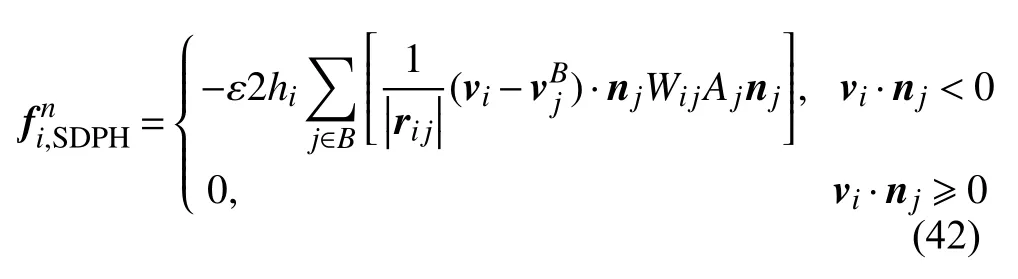
其中,ε 为罚参数,rij为粒子i和粒子j之间的径矢,vi为粒子i的速度矢量,为边界粒子j的速度矢量,nj为边界粒子j的法向向量,如图8 所示.Wij为粒子i和粒子j之间的核函数,Aj为边界粒子的面积.DEM 颗粒和边界之间的法向接触力采用方程(38)所示的赫兹模型[65]施加.
颗粒与边界之间的切向作用力fτ,采用摩擦模型计算.该模型认为颗粒与边界的切向力与法向力成正比关系

其中,t anφ 为颗粒流与边界的摩擦系数,φ 为摩擦角.
3 三维圆柱型颗粒堆坍塌过程数值模拟
颗粒堆坍塌问题是认识颗粒材料运动规律、检验模型方法有效性的基础案例.很多学者已经对二维单侧颗粒堆坍塌过程进行了数值模拟,但由于在厚度方向受限于前后壁面的制约,很多三维的现象无法获取.同时,之前的坍塌过程数值模拟工况仅限于长径比较小的案例,颗粒基本上远离快速流态化状态,也就是基本是处于类固态和类液态,采用浓密颗粒介质的本构理论便可实现有效计算,但对于长径比较大的案例未曾涉及.这里选取不同长径比下的轴对称圆柱型颗粒堆坍塌算例进行数值模拟,捕捉全三维颗粒堆坍塌过程中一些典型现象,如截锥形结构、圆锥形结构、圆球形顶部结构以及墨西哥帽结构等,检验新的理论和方法在描述这种全三维、多相态问题上的有效性,同时深入认识和理解其物理机理.
算例模型示意图如图9 所示.三维圆柱型颗粒堆高度为H0,半径为R0(具体数值根据工况不同而发生改变),长径比用a来表示,a=H0/R0.在实验过程中,初始由空心圆形容器固定,在t=0 时刻,将空心圆形容器沿垂直方向提升,并假定容器移除速度非常快,颗粒流不受其影响.而数值模拟实施过程中,颗粒堆从零时刻开始计算,即表征圆形容器已经移除.颗粒介质由初始静止状态,开始沿径向塌陷,重力势能转化为运动动能,像流体一样流动.在流动的过程中,存在于颗粒堆中的能量逐渐耗散,流动逐渐转变为准静态状态,流速降低,流动性减小,形成一个对称的堆积体.假定最终沉积时的状态中颗粒介质的高度用Hf,半径用Rf表示,通过相关实验研究[14-16]表明,颗粒的材料、粒度、表面粗糙度以及初始颗粒堆的几何形态均对最终的沉积形态以及颗粒流的运动过程具有显著的影响,其中,初始长径比起着至关重要的作用.因此,本文重点通过改变结构的初始参数(堆体的高度、半径和体积)获得颗粒流动的标度定律,与实验进行对比验证.同时,通过分析浓密颗粒流中颗粒的流动以及最终沉积规律,揭示形成不同流动特征的机理,为实际自然现象规律的揭示提供支撑.

图9 模型示意图Fig.9 Geometric model of granular pile
算例中的颗粒材料设定为干燥无黏性沙子,颗粒直径为0.32 mm,实际密度为2600 kg/m3,初始体积分数为0.6,体积密度为1560 kg/m3,弹性模量为20 GPa,泊松比0.3,内摩擦角30°.采用SDPH 方法进行初始离散,SDPH 粒子的密度为颗粒的有效密度1560 kg/m3,初始体积分数为0.6,SDPH 粒子的直径为5 mm,粒子总数量根据工况不同而发生改变,光滑长度为6.5 mm.底部边界与颗粒之间有法向作用力和切向摩擦力存在,法向接触力按照阈值函数方法计算,切向摩擦力按照摩擦模型计算,摩擦力系数 t anφ=0.6 .该算例中,决定相态转变的体积分数临界值来源于不同模型的适用范围数值,属于经验参数,这里取 φl,min=0.55,φg,max=0.5,φg,min=0.02 .
首先,为了验证本文所选取的SDPH 粒子直径的合理性,在长径比a=0.72 条件下对改变不同的SDPH 粒子初始直径进行了计算,并与文献实验结果[6]进行了对比,如图10 所示.从结果来看,随着初始粒径的减小,计算的精度也越高,但是计算量随之增加,初始粒径为5 mm 与2.5 mm 的结果相差较少,同时与实验吻合较好.因此,为了保持足够的精度,同时计算量又得到控制,本文选取的直径5 mm 是较为合理的.
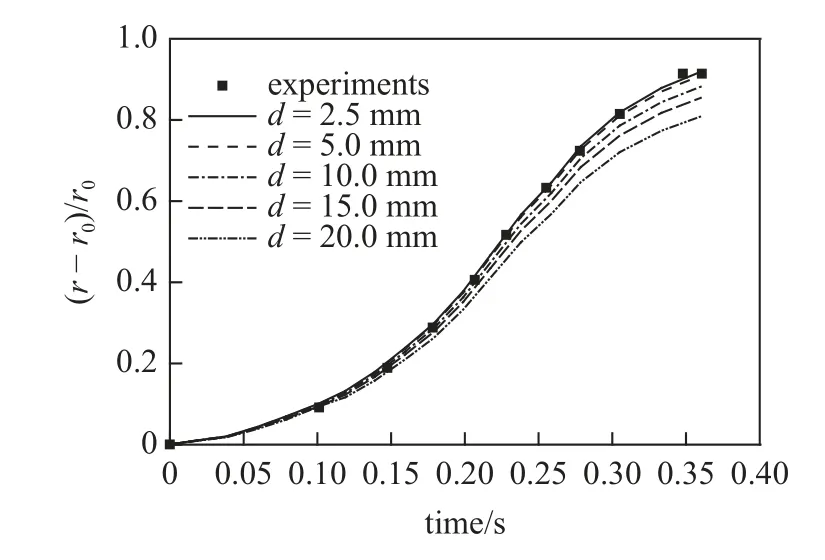
图10 不同SDPH 粒子直径下计算结果与实验[6]对比Fig.10 Comparison between calculated results and experiments[6]under different SDPH particle diameters
图11 为计算获得的在a=0.55 工况下不同时刻的颗粒运动过程及最终沉积形态图.可以看到,在150 ms 时刻,处于圆堆体上部外层的颗粒已经开始斜向下、向四周坍塌运动,而处于内层的颗粒则一直处于静止状态,它们之间存在一个明显的间隔面将外部坍塌区域与内部非变性区域分开,这在固体力学领域称为剪切带.随着时间的发展,剪切带进一步向内部中心移动,外层坍塌的区域进一步扩展.由于底部摩擦力的作用以及颗粒-颗粒间接触作用和重力作用的共同影响,在最终颗粒停止运动后,在堆体顶部留有一部分未受任何干扰的区域,形成类似“平头帽”状形态,该区域保持在初始高度H0,并且其与周围自由表面坡形成一个约为静态休止角的状态.
图12 为计算获得的在a=0.9 工况下,不同时刻的颗粒运动过程及最终沉积形态图.相比a=0.55 工况下的计算结果,该流动更加复杂.它不像a=0.55工况下直接在静态区和非静态区之间形成分割面,而是由外层一层层向内坍塌扩散,分割面不清晰,自由表面的坡度从流动前沿到堆体的上顶部逐渐变陡.随着屈服颗粒一层层的发展侵蚀,最终整个颗粒堆的上表面完全达到屈服状态,仅在最高峰处留下一个尖尖的锥形角,最终形成的坡度的角度也明显小于静态休止角.与图11 不同的是,由于该工况下最终堆积形态的最高峰不再是初始高度值,因此数值模拟结果采用高度等高线进行云图显示.通过图像可以看出本文的数值模拟很好地捕获到了该实验现象,与实验图像吻合非常好.

图11 a=0.55 工况下颗粒堆坍塌过程与实验[6]对比Fig.11 Comparison of the calculated collapse of the granular column with that of the experiment[6] under the condition of a=0.55
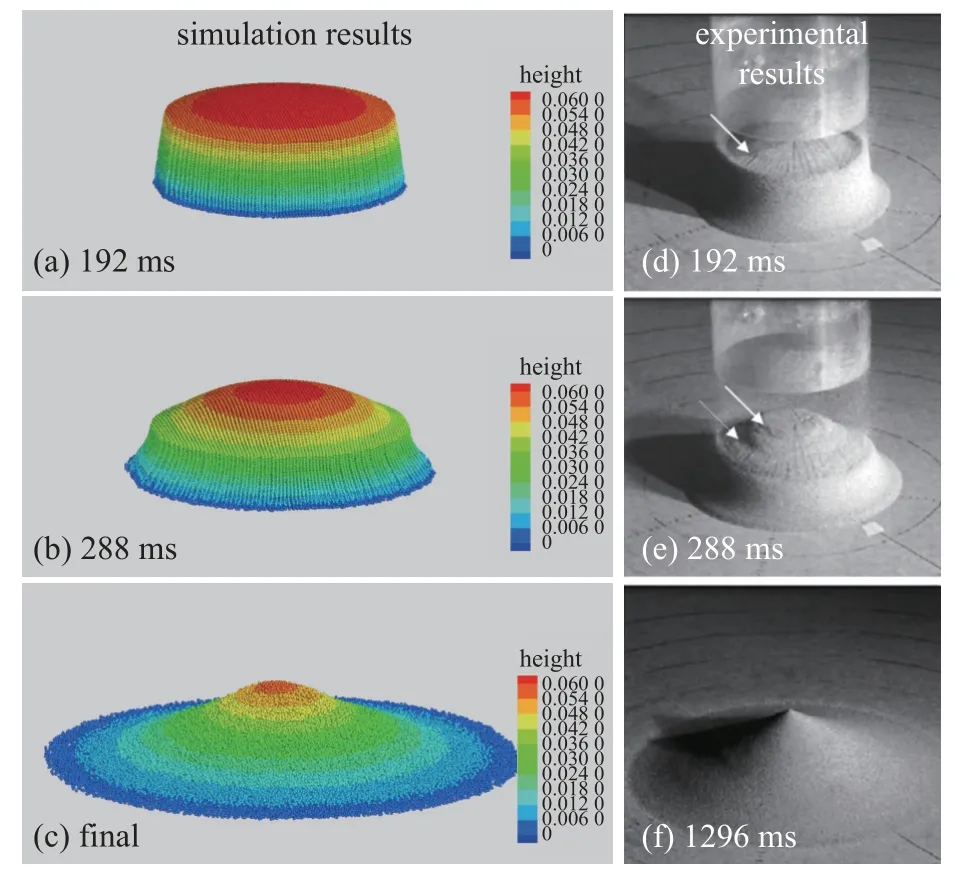
图12 a=0.9 工况下颗粒堆坍塌过程与实验[6]对比Fig.12 Comparison of the calculated collapse of the granular column with that of the experiment[6] under the condition of a=0.9
图13 为a=3.0 工况下颗粒堆在不同时刻的运动过程形态计算结果与实验对比.可以看出从0 时刻开始整个上表面开始向下运动,位于堆体底部外侧的颗粒则开始向外运动,在颗粒堆前沿两侧观察到较大的速度.由于堆体高度较大,堆体顶部的粒子以较高的速度坍塌,可以看到处于堆体周围的颗粒已经有少部分处于快速相态化状态,但位于堆体顶部的颗粒表面形态不发生改变.在堆体向下运动一段距离后,由于堆体周围颗粒受重力和剪切力作用,堆体顶部变形形成一个凸形圆顶形态,其曲率半径也随着时间的发展而逐渐变小.由于水平面上速度较大的粒子可以在水平表面的两个方向上同时对称地运动,因此,其逐渐转变成正弦函数的形状.通过与Lajeunesse 等[9]通过剖开颗粒堆积体形态可以看到,最终的形态可以分为三个区域,一个是中心未发生任何改变的静态区域,半径与初始堆体半径相同;一个是颗粒流先到达的区域;另一个是外部的扩展流动区域.本文数值模拟同样观察到了该现象,与实验吻合较好.
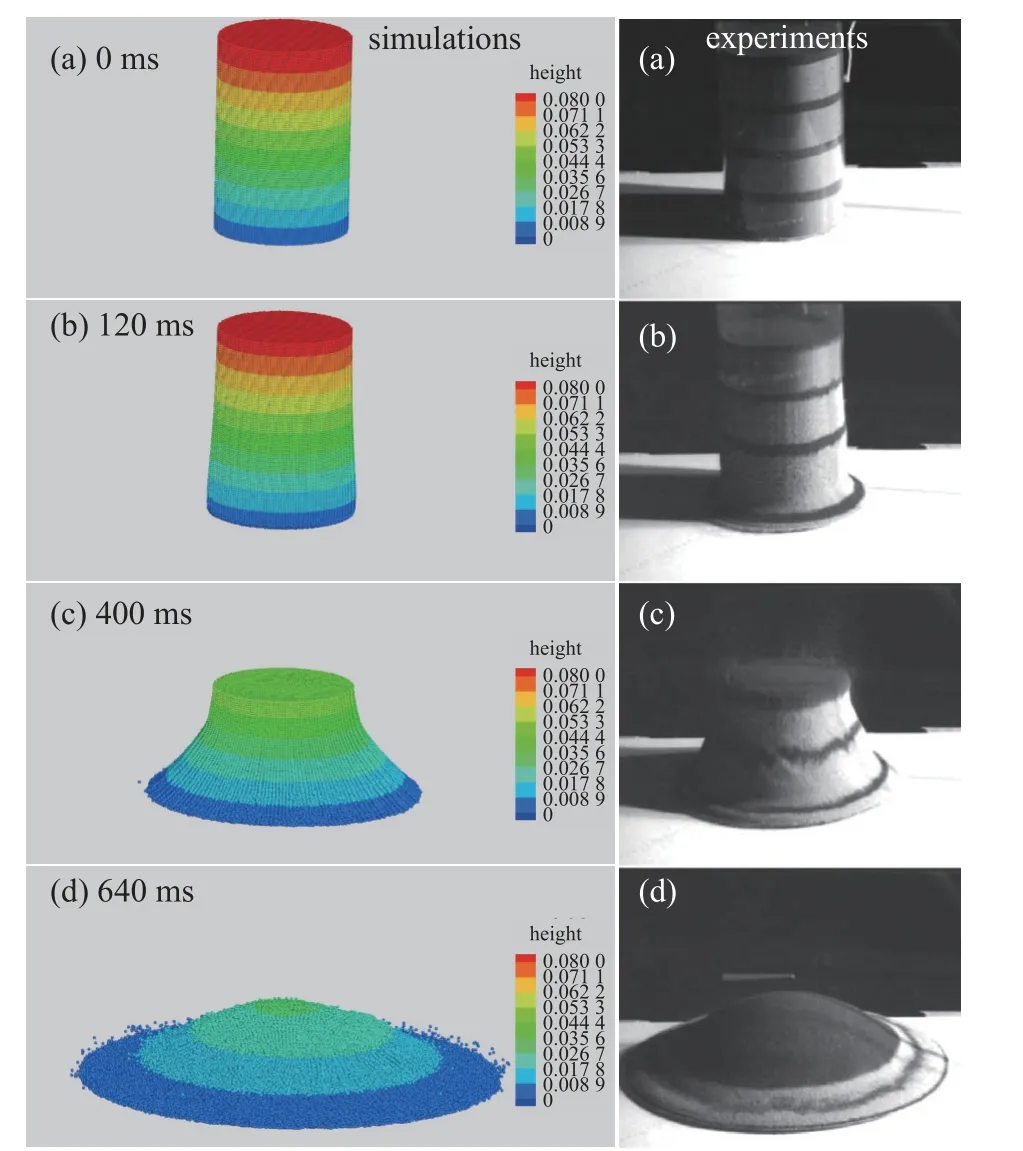
图13 a=3.0 工况下颗粒堆坍塌过程与实验[6]对比Fig.13 Comparison of the calculated collapse of the granular column with that of the experiment[6] under the condition of a=3.0
继续增大初始长径比至a=13.8,颗粒堆的表面速度扩展更大,从图14(b)和14(c)显示的堆体部分颗粒的分布即可看出,堆体表面的颗粒已经出现很大的速度波动,处于明显的快速相态化状态.在484 ms 上部堆体已经完全消失,由于向下运动的颗粒堆速度较高,到达铺展表面的颗粒仍有垂直向下运动的趋势,造成对于铺展表面颗粒堆的冲击,中心铺展区域形成一个环形凹状结构,随着时间推移,凹状结构进一步扩大,同时能量进一步耗散,直到514 s 后基本达到稳定状态.在此基础上进一步增大长径比至a=16.7,如图15 所示,凹状结构更加明显,形成明显的墨西哥帽形态,中心是一个尖型的锥角,四周形成一个脊状.通过与实验对比,除了中心锥角的角度稍大于实验获得的锥角角度之外,脊状的位置、脊状的高度、铺展的范围等数值均与实验[6,10]吻合较好.
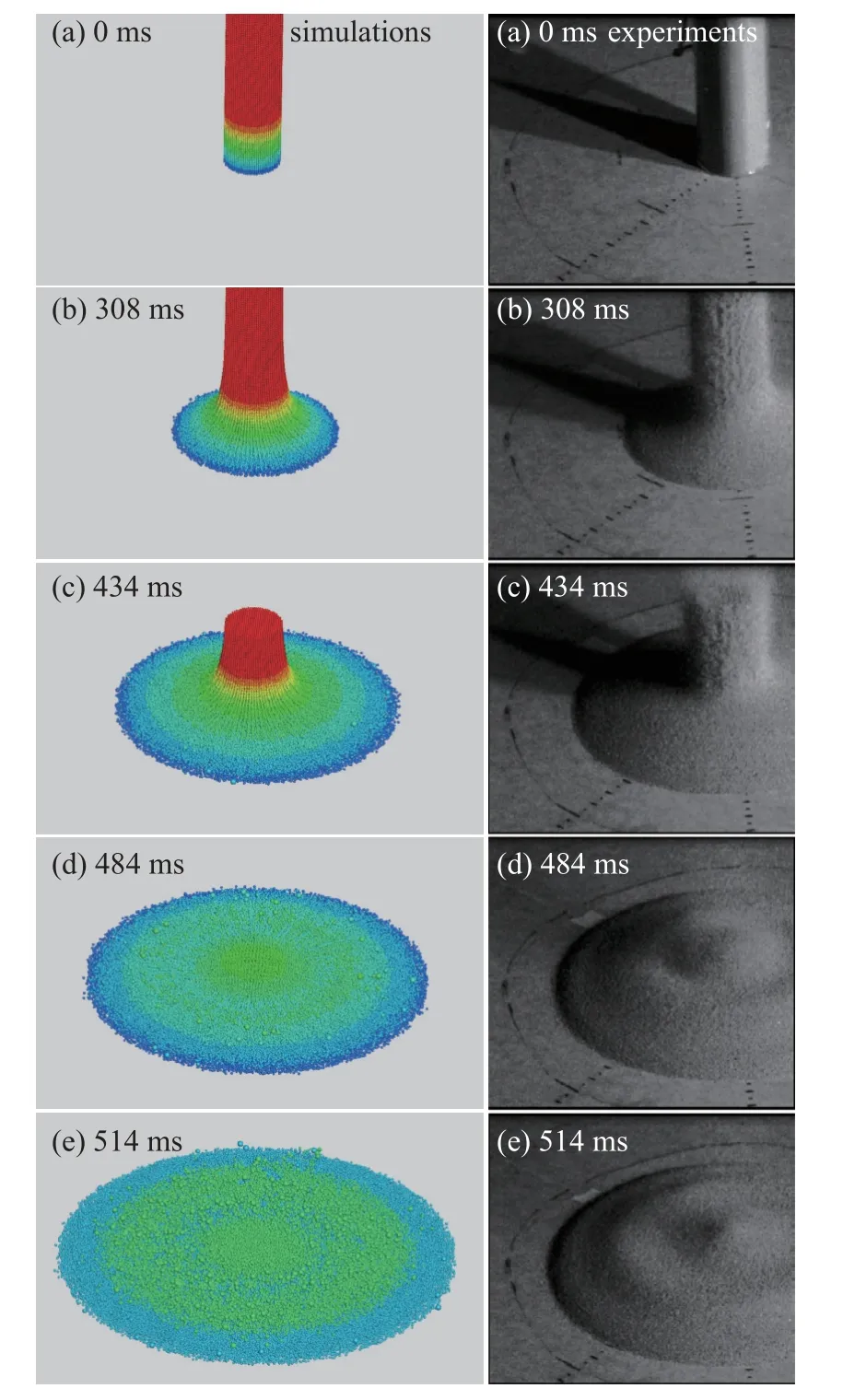
图14 a=13.8 工况下颗粒堆坍塌过程与实验[6]对比Fig.14 Comparison of the calculated collapse of the granular column with that of the experiment[6] under the condition of a=13.8
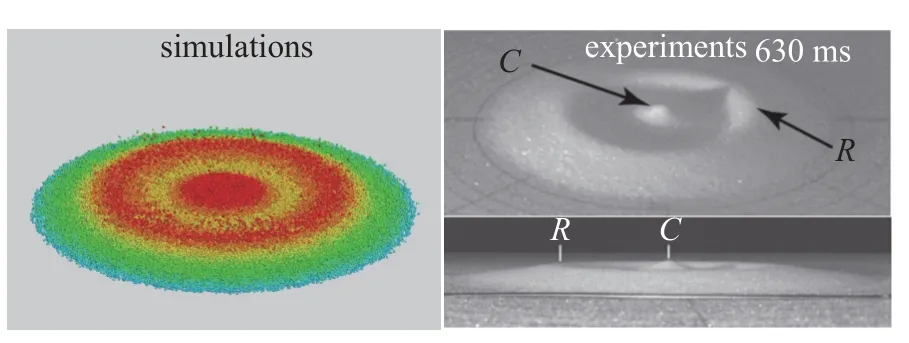
图15 a=16.7 工况下颗粒堆最终铺展形态与实验[10]对比Fig.15 Comparison of the calculated final spreading morphology of the granular column with that of experimental results[10] under the condition of a=16.7
在本文模拟算例中,对于较大长径比的三维颗粒堆来说,其颗粒运动的速度较大,铺展的范围也很大,存在一些颗粒从主体颗粒堆中分离出来,不再遵循颗粒的类固态和类液态假设.颗粒的体积分数变化较大,颗粒之间的接触不再以长时碰撞接触为主,属于快速颗粒流动,具有较大的惯性数,剪切速率较高,堆积的围压接近于零,这时必须采用类气态颗粒流模型和离散单元模型进行求解.
图16 展示了a值为16.7 条件下颗粒堆在坍塌中所经历的不同相态过程,黑色表示颗粒处于浓密态(颗粒固相和液相),红色表示颗粒处于稀疏态(颗粒气相和液气过渡状态),白色表示颗粒处于超稀疏态(颗粒离散惯性相).可以看出,由于初始长径比较大,颗粒到达壁面铺展时速度较高基本上均处于快速颗粒流状态,而处于边缘附近的部分少数颗粒由于速度更大,体积分数较小,基本上脱离颗粒堆的运动,达到超稀疏状态,计算很好地捕捉到了相态演变过程.

图16 a=16.7 三维圆柱型颗粒堆坍塌过程不同相态演变(黑色表示颗粒处于浓密态,红色表示颗粒处于稀疏态,白色表示颗粒处于超稀疏态)Fig.16 The evolution of different phases during the collapse of cylindrical granular pile (Black indicates that the particles are in dense state,red indicates that the particles are in dilute state,and white indicates that the particles are in ultra-dilute state)
图17 为a<1.7 情况下颗粒铺展范围随高径比的不同变化曲线,该曲线理论上是一条线性直线,因为在这个长径比范围内,颗粒铺展的范围有限,中心部分的颗粒堆基本保持不变,只有超出一定半径范围之后的颗粒参与铺展运动,初始颗粒堆的高度直接决定了该铺展范围,而与初始的颗粒堆半径无关,因此该直线等价于铺展范围r∞−r0与初始颗粒堆高度h0之间的关系.从量纲角度分析其必定是线性关系,实验拟合数据比例系数为1.24,从图17 可以看出数值模拟结果与实验结果[6]对比较好.
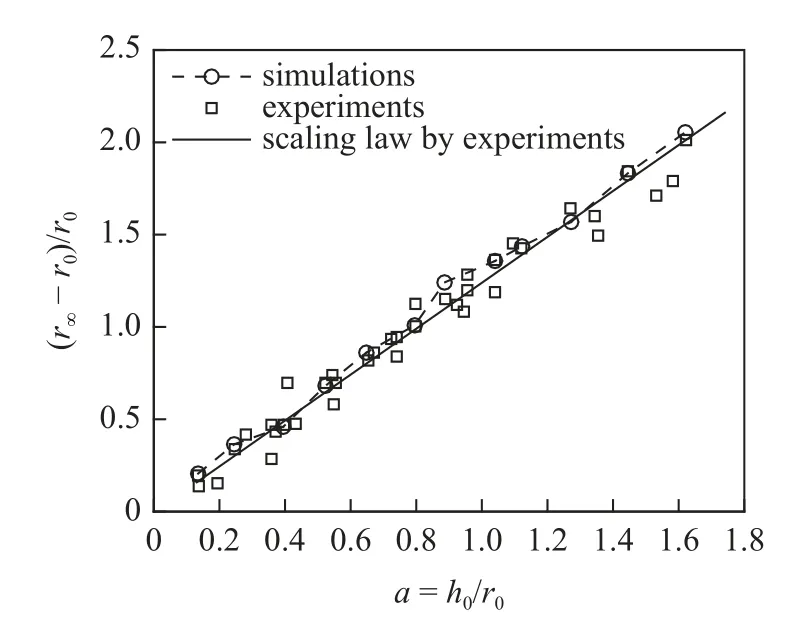
图17 颗粒堆铺展范围随着a 不同的变化曲线(a <1.7)Fig.17 The runout range of the granular column as a function of a (a <1.7)
图18 为不同a值条件下颗粒堆高度与铺展范围半径之间的关系曲线,可以看出在a值较小的情况下(a<1.0),由于颗粒堆顶部部分中心颗粒未受到坍塌扰动作用,其高度与铺展面积之间无相关关系.在1 .0 图18 不同a 值条件下颗粒堆高度与铺展范围半径之间的关系曲线Fig.18 The height of the granular column as a function of spreading radius under different conditions of a 图19 为三种不同a值条件下颗粒堆铺展范围随时间变化曲线,随着a值增加铺展的时间增长,铺展的范围增加,曲线基本上呈S 形,在初始阶段铺展的较为缓慢,主要与速度启动存在一定的滞后有关,最终在底部摩擦力和内部剪切作用力下能量耗散,缓慢回到静止状态.从数值模拟结果和实验[14]对比可以看出,两者数据吻合较好. 图19 颗粒堆铺展范围随时间变化曲线Fig.19 The runout range of the granular column over time 最后,为了展示本文所采用的数值方法在计算效率方面的优势,对相同工况(a=0.55)和相同粒子数情况下采用本文方法和DEM 方法的计算耗时进行了对比,具体DEM 计算是采用商业软件EDEM 2018 完成.对比数据如表1 所示.由于DEM 方法时间步长受颗粒的硬度和直径影响较大,无法采用更大的时间步长.而SDPH 方法虽然也受颗粒属性的影响,但是该颗粒属性为宏观局部的平均值,计算获得的时间步长更大些.因此,计算获得同样的结果,DEM 计算的总步数较多,同时每一时间步对于接触力的计算耗时相较SDPH 方法来说也较大一些,总耗时较长. 表1 本文方法与DEM 方法计算耗时对比Table 1 Comparison of calculation time between this method and DEM method 论文针对三维圆柱型颗粒堆坍塌过程中表现出来的堆积、缓慢流动、快速流动、分离流动等不同相态问题开展了数值模拟研究,成功再现了不同工况下的颗粒堆坍塌过程,获得的主要结论如下. (1)建立的全相态物理模型和数值方法对于颗粒介质运动过程中呈现出来的不同相态可以较好地捕捉,同时由于采用的数值方法中除了超稀疏区域外均为基于连续介质力学的粒子类方法,计算所使用的参数均是宏观实验可获得的参量,克服了采用单一单颗粒轨道追踪依赖于单颗粒属性的缺陷;同时,采用的粒子方法属于粗粒度方法,既可以实现对颗粒的拉格朗日运动轨迹再现,又可以降低实际单颗粒建模所带来的计算量大的问题. (2)三维圆柱型颗粒堆在不同初始高宽比条件下最终沉积物形态存在较大的差别,可形成平凸形、尖角形、圆顶形、墨西哥帽形等,在高宽比小于1.7 范围内颗粒堆铺展范围与高宽比近似成直线形关系. (3)虽然本文采用基于连续介质力学模型的数值方法对颗粒介质运动问题模拟计算取得了较好的结果,但不可否认此类方法也存在一定的局限:一方面此类方法必须依赖于连续介质力学模型的发展,而颗粒介质的宏观理论预测模型目前尚属于发展阶段,还需要不断改进和完善;另一方面此类方法描述的是物质的连续介质力学行为,每个单元参量表征的是物质局部的统计平均特性,即使本文采用粒子方法获得了颗粒的运动轨迹,但是这种粒子是属于一种“伪颗粒”,而非真实的颗粒,无法获得真实单颗粒的运动特征以及真实单颗粒间的相互作用行为;第三方面由于此类方法计算颗粒运动问题经历了连续介质力学模型的建立和数值模拟方法的使用两个关键过程,每个过程中均存在一定的假设和简化,理论上计算的精度相比单颗粒直接模拟的微观方法来说存在一定的差距,需要不断发展和提高物理模型和数值方法的准确度.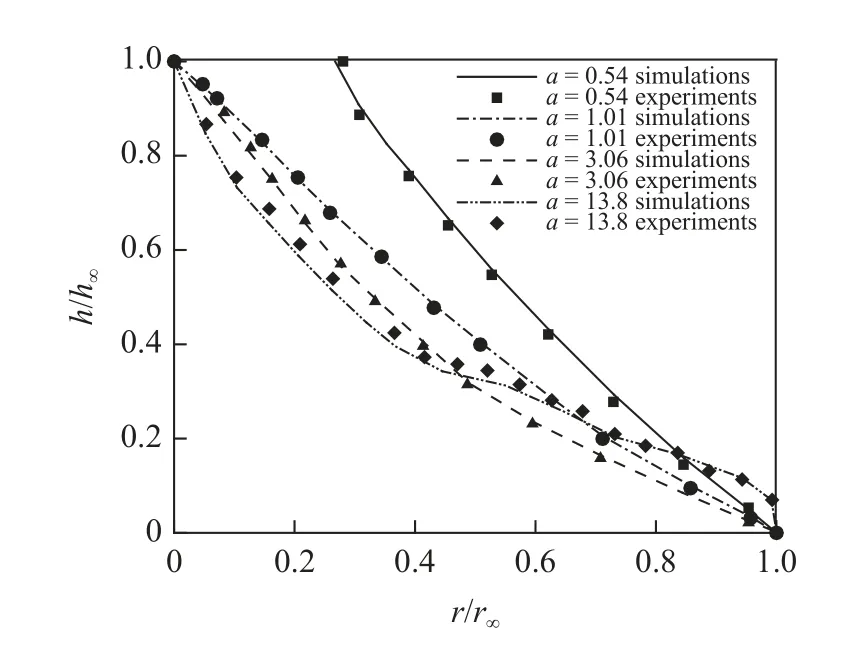


4 结论

