碳氢燃料超声速燃烧分区实验研究1)

孟凡钊 周芮旭 李忠朋 连 欢,)

* (中国科学院力学研究所,高温气体动力学国家重点实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

引言

超燃冲压发动机燃烧室内氧化剂与燃料需要在极高速来流条件下实现高效掺混与稳定燃烧.双模态冲压发动机燃烧室内影响发动机工作性能的流动过程,通常认为是亚燃工作模态下的预燃激波串结构以及超燃工作模态下的超声速剪切流动结构[1-2].双模态冲压发动机燃烧室内的超声速燃烧与流动耦合问题通常主要关注凹腔结构大尺度涡结构,形成低速回流区稳定火焰燃烧.以及超声速横向射流诱发涡结构,形成气动反压减速来流,形成尾迹低速区稳定火焰燃烧[3-4].以上几种流动以及流动与燃烧的耦合作用由于对双模态冲压发动机性能作用明显,近几十年研究较为充分[5-10].

然而可压缩湍流场的时空多尺度特性以及与超声速燃烧的多尺度耦合关系是超声速燃烧更为本质的基本科学问题.受限于实验设备和测试技术,目前尚未见到相关实验研究,主要采用数值模拟与理论结合的方式[11-17]开展研究.但由于对超声速燃烧本质基本科学问题的认识不清,制约了数值发动机技术和发动机研制水平的发展.由此,构成了本文关注的基本科学问题.

超声速湍流燃烧复杂的相互作用通常在多特征尺度范围内均存在,使得超声速湍流燃烧问题难以解耦和简化.一方面,燃烧情况受到湍流涡的干扰,导致燃烧特性的改变,如火焰形状和火焰面厚度等;另一方面,由于燃烧释热导致压力和局部流体性质的变化,如密度、黏度和扩散系数等导致湍流场的结构和动力学性质的改变.Borghi[18]通过理论分析与实验方法相结合的方式提出了完全预混条件下的燃烧分区理论,对上述耦合过程进行了有效简化,奠定了湍流燃烧研究的基础.文献[19]将燃烧分区理论扩展到了超声速部分预混燃烧情况,给出了火焰分区的判别方法.

在不可压缩完全预混湍流燃烧模型中,常用以下五个参数来表征火焰分区:lk/δl,L0/δl,Re,Da,v′/Sl,其中L0为湍流的积分尺度,lk为湍流耗散尺度,δl为火焰面厚度,v′为湍流脉动速度,Sl为层流火焰速度.这些参数划分了三种不同的火焰分区:分布反应、皱纹层流火焰和波纹火焰.此外,在湍流中还有一个重要的尺度参与了火焰分区的划分,即泰勒尺度lλ,介于积分尺度和耗散尺度之间.这些参数之间的关系为

其中,µ 为动力黏度,tflow为流动的特征时间,tchem为燃烧的特征时间.由湍流雷诺数Re和丹姆克尔数Da关系可知

将湍流雷诺数Re和丹姆克尔数Da之间的关系作图即可得到典型的燃烧火焰分区图[19].如图1 所示,根据火焰面厚度与湍流尺度相对大小将火焰分区划分为以下三种.

图1 Ingenito 等给出的火焰分区分布Fig.1 Flame mode distribution given by Ingenito

(1)褶皱层流火焰区域,位于A 区域,此时火焰面厚度小于湍流耗散尺度,燃烧在很薄的区域进行,以快速化学反应为主.

(2)旋涡小火焰区域,位于B 区域,此时火焰面厚度在湍流积分尺度与耗散尺度之间,超声速燃烧一般均发生在该区域.在B 区域,湍流场涡结构不仅对火焰面厚度和形状有影响,对局部输运现象也会造成不同程度的影响,具体与飞行条件有关.Da较大时,火焰面厚度小于泰勒尺度,此时为快速化学反应,湍流场小涡结构起到主导作用,称为B1 区域.而Da较小时,火焰面厚度大于泰勒尺度,此时为慢速化学反应,湍流场大涡结构起到主导作用,称为B2 区域.而快慢化学反应的分界线主要与泰勒尺度有关,在低马赫数情况下,刚好对应于Da=1,但随着Ma增加,可压缩性影响逐渐增强,该分界线会随之上移[19],约为 1 +2Ma2.

(3)分布反应区域,位于C 区域,此时火焰面厚度大于湍流积分尺度,所有的湍流特征尺度都在反应区,该区域燃烧受湍流影响最大.

超声速湍流燃烧数值模拟通常基于输运PDF(probability density function) 模型[20]、火焰面模型[21-22]、条件矩模型[23-24]、线性涡模型[25]等模型假设和方法.由于对超声速湍流燃烧基本科学问题认识不清,每种模型的适用性不明确因此存在一定的局限性.设定型 PDF 由于不能准确估算化学反应源项的高阶关联量导致存在一定的计算误差[26],同时湍流燃烧过程中涉及了多时空尺度以及多组分化学反应问题导致系统复杂度与计算量的激增,基于输运PDF 模型的超声速湍流燃烧高保真数值计算由于依赖于混合模型以及采用 Monte-Carlo 方法而计算量巨大,需要至少千万量级的网格数[12,27].由于相对具有较快的计算速度,火焰面模型应用更为广泛,其模型计算量并不随着化学反应系统复杂度的增加而明显增大.目前,基于火焰面模型的超声速燃烧数值模拟[21-22,28],通过数值模拟以及Chemkin 软件等对流动和燃烧时间尺度进行估算来判别火焰分区,通常进行小火焰模型假设,以扩散火焰为主,以高丹姆克尔数Da为主要特征[11-17,29-30].超声速燃烧反应的特征尺度小于湍流Kolmgorov 耗散尺度,受到湍流场的影响较小,在燃烧反应区内主要考虑分子扩散与化学反应的动态平衡.而由于碳氢燃料多步化学反应与流场燃烧场耦合较为复杂,因此上述火焰面模型研究多以氢气燃料为主,文献[26,28]等研究表明氢气燃料的超燃冲压发动机,其燃烧过程中主要为扩散火焰,输运过程以分子扩散为主,湍流影响有限.对于碳氢燃料燃烧分区的数值仿真研究相对较少,其中李晓鹏等[31]等开展的碳氢燃料仿真结果表明,碳氢燃料超声速燃烧不仅是分子扩散主导输运过程,湍流影响不可忽略.

综上所述,目前对超声速燃烧火焰面模型适用性以及分区燃烧物理模型认识不足,并且受限于实验设备和测试技术尚未见到相关实验研究.本工作基于自主研发的MHz 发动机内窥光纤传感器,针对单边扩张双模态冲压发动机超声速燃烧火焰分区开展实验研究,通过化学自发光信号的最小香农熵定义超声速燃烧的特征时间tchem,结合Sutherland 理论[32],对燃烧室内燃烧分区进行判别,验证了碳氢燃料超燃冲压发动机典型飞行工况下燃烧室内超声速燃烧处于旋涡小火焰区域(Re≅ 50000;Da∈1.80-2.60,B 区),湍流发挥重要作用,并给出了当量比、通量比以及马赫数对燃烧特征时间的影响规律.

1 实验方法

1.1 超声速燃烧直连实验台

中国科学院力学研究所研制的连续变马赫数直连实验台主体由流量动态调节气源、可调加热器、可调喷管以及实验段组成[33].图2 为示意图.通过压力调节阀实现空气、氢气、氧气流量动态调节,采用环形多孔喷注中心燃烧的烧氢补氧方式对来流进行加热,通过气源流量动态调节实现加热器内模拟总温总压实时可调,可调喷管型面按照高低马赫数双设计点非对称方法设计,由机电伺服机构驱动改变喉道面积实现模拟飞行马赫数实时调节.可调加热器和可调喷管均采用水冷热防护.流量动态调节气源、可调加热器、可调喷管通过PLC 工业控制系统进行精确时序控制,接受实验控制台操作指令,并根据指令执行流量调节、伺服机构运动等相应动作,同时具有实验台主体气源压力、直连台双螺柱安装型推力传感器数据采集和处理能力.实验台模拟最大气体流量 2 .5 kg/s,最高总温1900 K,最高总压 4 MPa,最长工作时间 30 s,模拟飞行马赫数范围4.5～6.5.实验段为截面为 80 mm×40 mm 的等截面隔离段和单边扩张双凹腔燃烧室模型,其中隔离段长度为 337 mm,燃烧室模型下壁面扩张角为2°,凹腔位于隔离段入口下游 447 mm 处,长度为65 mm,深度为 17 mm,倾角为22.5°.凹腔上游 60.5 mm 安装乙烯喷块.此外,凹腔底部安装火花塞辅助点火.

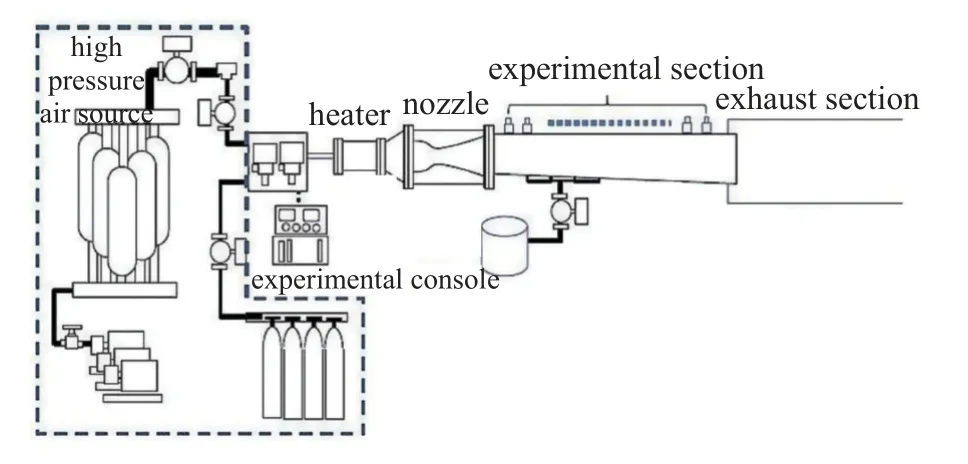
图2 直连式超声速燃烧实验台示意图Fig.2 Schematic diagram of direct connected supersonic combustion test bench

本文报告的实验全部使用气态乙烯燃料,具体实验工况如表1 所示.主要涵盖了三种实验条件的变化,当量比Ф、动量通量比J以及来流马赫数Ma.通过乙烯喷注压力实现燃料质量流量和当量比Ф调节;同时采用了三种不同孔径的燃料喷孔,实现相同质量流量(当量比Ф=0.17)条件下,燃料动量通量比J的变化;除以上定常实验以外,通过改变喉道面积,模拟了来流马赫数Ma动态变化的加速上行模拟实验.

表1 实验工况Table 1 Experimental conditions

本次地面模拟实验,前五种工况为定常实验,燃烧室入口马赫数Ma=2.8,实验有效时间为 2 s .一组变马赫数加速上行的非定常实验,燃烧室入口马赫数Ma=2.5 ∼2.8 ∼3.0 线性变化,实验有效时间为 7 s .全部实验均是总温 1475 K、总压1678 K,加热气体总流量 1379 g/s .

首先分析并判别本次六组实验工况的燃烧模态情况,在此基础上展开本文的主要研究内容,即超声速燃烧特征时间的分析.前五种工况定常实验中间时刻以及加速上行实验不同时刻的沿程压力分布和一维马赫数分布如下图所示.其中,图3 及图4 表示通过改变乙烯燃料喷注压力,实现燃料质量流量和当量比调节,实现由工况1 超燃工作模态向工况3 亚燃工作模态的转变.

图3 当量比变化时沿程压力分布Fig.3 Pressure distribution along the model of different stoichiometric ratios

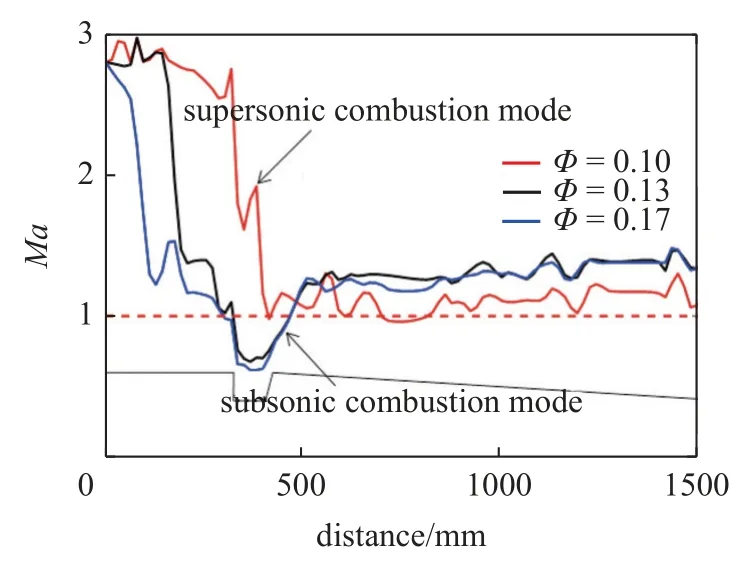
图4 当量比变化时一维沿程马赫数分布Fig.4 One-dimensional Mach number distribution along model of different stoichiometric ratios

图5 及图6 表示三种不同孔径的喷孔,实现相同质量流量(当量比Ф=0.17)条件下,燃料动量通量比的变化,可见在与当前燃烧室构型组合条件下,高通量比通过实现增强混合提高了释热量.通过不同当量比和通量比对比可以发现,当量比的变化显著影响释热,通量比变化对释热存在的影响有限.

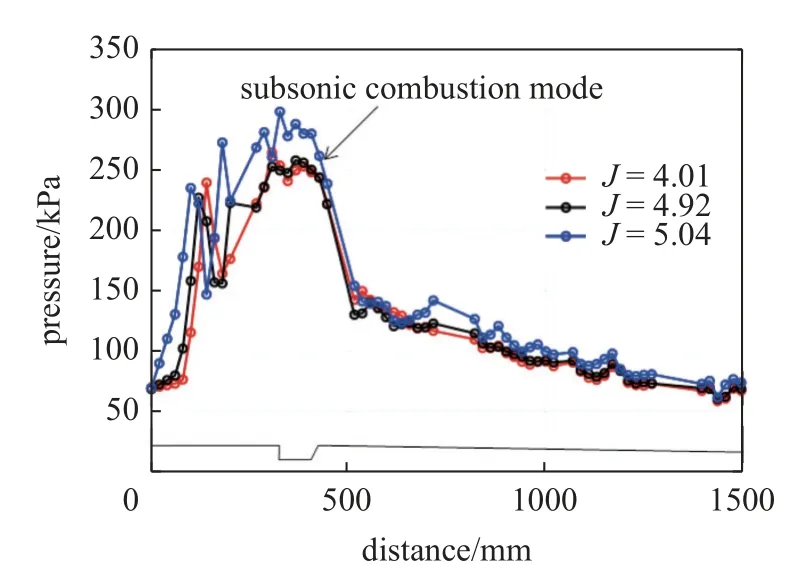
图5 动量通量比变化时沿程压力分布Fig.5 Pressure distribution along the model of different momentum flux ratios

图6 动量通量比变化时一维沿程马赫数分布Fig.6 One-dimensional Mach number distribution along model of different momentum flux ratios

加速上行实验结果如图7 和图8 所示,受马赫数变化的影响,不同时刻的沿程压力以及马赫数变化较小,均处于亚燃模态.本文对于超声速燃烧火焰分区的判断基于此六组具有代表性的实验,定量分析共性的燃烧特征时间和火焰分区实验规律.

图7 加速上行飞行轨迹沿程压力分布Fig.7 Pressure distribution along the model of acceleration experiment

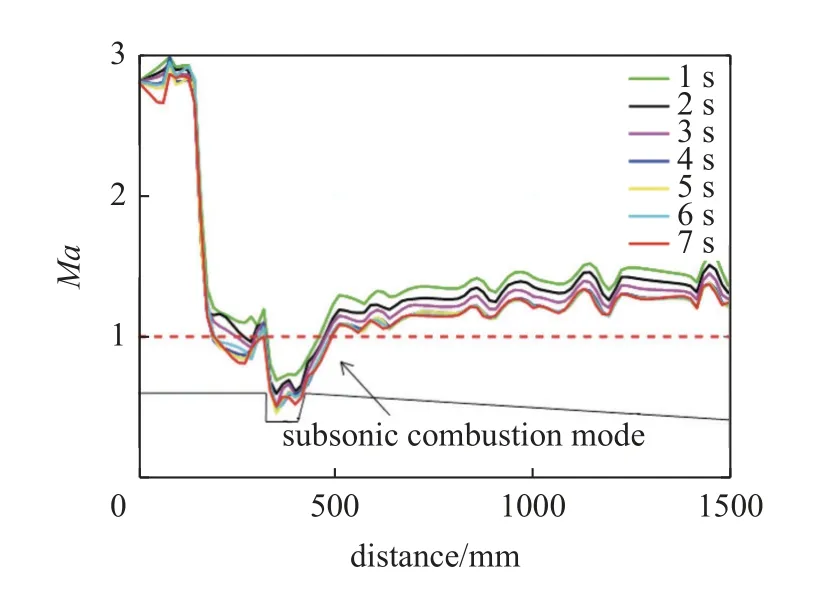
图8 加速上行飞行轨迹一维沿程马赫数分布Fig.8 One-dimensional Mach number distribution along the model of acceleration experiment

1.2 实验测量系统

针对发动机燃烧室极端力热环境以及难以开设光学窗口的机构特点,团队自主研发了动态频响应200kHz,采样率1 MHz 的被动内窥光纤火焰传感器测试系统[34],详细的系统描述以及超声速燃烧感知功能开发过程可参考该论文.内窥光纤火焰传感器测试系统主要包含光信号采集模块、光电倍增模块、模电转换模块、燃烧信号处理模块四个子系统,子系统接口和布局方式如图9 所示.

图9 被动式内窥镜火焰传感器测试系统示意图Fig.9 Schematic diagram of passive endoscope flame sensor test system

通过将内窥光纤火焰传感器与发动机点火器集成的结构设计方法,可确保无需在发动机燃烧室单独开设安装孔,实物图如图10 所示.点火器集成的光学测点布设方式可进一步实现对点火瞬态过程及凹腔回流区火焰燃烧特性的感知与分析.安装方式如图11 所示,集成后共有4 个光学观测窗口,分别对凹腔内不同位置火焰自发光信号进行MHz 采样率的化学自发光时间序列信号采集.

图10 点火器与传感器集成Fig.10 Igniter and sensor integration

图11 传感器安装位置示意图Fig.11 Schematic diagram of sensor position

2 实验数据分析方法

2.1 火焰质心定义方法

通过布设通道光纤测点定义火焰质心Xf的离散时间序列,可对超声速燃烧稳定性进行定性观测(图12)

图12 火焰质心定义原理示意图Fig.12 Schematic diagram of flame centroid definition principle

其中,ri和qi分别表示空间每个像素点i的矩阵坐标与像素值的大小,Q表示所有像素点值的总和.

2.2 最小香农熵定义超声速燃烧特征时间

基于动力系统理论的非线性时间序列分析为揭示非周期时间序列数据的动力学特性提供了重要的信息,对超声速燃烧稳定性进行定量描述.比如通过分形维数、Lyapunov 指数和熵等用于物理不变量的量化、非线性预测和降噪等技术应用.近期研究人员针对燃烧过程和火焰前缘不稳定性[35-41],重点研究了动力学中非周期性演化特征.比如相关维量化的自相似结构,最大Lyapunov 指数在相空间中的轨道不稳定性[42-45]表征等.

修正的香农熵[46]是对采样时长为T的时间序列随机性的定量度量.将该时间序列数据用一定的符号进行分割,利用分割数目N和时间调查窗口L离散化,来表征数据的时间相关性.本文采用修正香农熵的方法,参考湍流特征时间的经典定义方法,通过燃烧信号的时间自相关性定义超声速燃烧的特征时间 τsc,详细推导过程见附录.如图13 和图14所示,首先对直接测量的燃烧自发光 C H∗时间序列信号Ii进行等概率区间N、多时间调查窗口L的离散化处理,针对特定[N,L]组合计算表征直接测量时间序列的时间相关性的信息香农熵Hs(N,L) .化学自发光燃烧时间序列信号Ii可表示为

图13 工况1 中P1 测点自发光 C H∗ 信号Fig.13 Self-luminous C H∗ signal of P1 point in experimental condition 1

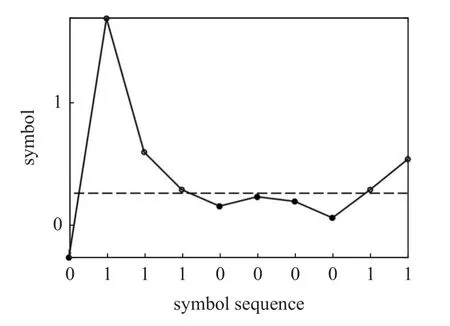
图14 N=2 时 C H∗ 信号离散化示意图Fig.14 C H∗ signal discretization diagram when N=2

其中 ∆=1 μs,表示序列的时间分辨率,目前为1 μs,由测量系统硬件参数决定;k表示时间序列长度.

之后将离散后的信号进行修正香农熵的计算

其中,Pk表示在时间调查窗口为L和符号分割数目N一定时,每组调查序列出现的概率.nseq表示不同类型调查序列的总数.当香农熵Hs等于1 时,表示该系统完全随机;当香农熵Hs小于1,表示该系统存在确定性机制,香农熵越小确定性越强.而随着调查窗口L和符号分割数目N不同,香农熵会随之改变,但存在极小值点.

如图15 所示,工况1 采样时长为 5 ms,即T=k∆=5 ms(k=5000),对应的不同[N,L]离散方式下的香农熵分布图Hs(N,L),由图可知,离散信号[N,L]不同,香农熵数值随之变化.计算最小香农熵,此时燃烧自发光 C H∗时间序列具有最强的系统时间相关性和确定性,其对应的时间调查窗口L所表征时间即为燃烧特征时间.由此本文采用燃烧自发光 CH∗时间序列信号最小香农熵定义并计算了不同工况下的超声速燃烧的特征时间.

图15 T=5 ms 时工况1 下 P1 测点测得的香农熵Fig.15 Shannon entropy measured at P1 point under experimental condition 1 when T=5 ms

由以上分析可知,对于实验有效时间内特征时间的计算除了与离散过程中调查窗口L和符号分割数目N有关以外,每个时刻选取计算香农熵的采样时长T也会对最终结果有所影响.因此,改变采样时长T,验证香农熵计算结果对采样时长的敏感性.计算实验有效时间内三个不同时刻的燃烧特征时间随着采样时长T的变化情况,结果如图16 所示,由最小香农熵计算得到的燃烧特征时间,在采样时长T=1.2 ms 及更大时逐渐收敛.并且由图17 可知,当T=1.1 ∼1.3 ms时,燃烧特征时间的标准差处于较小值,均在0.2 以下.因此,同时综合考虑计算量等因素,选取T=1.2 ms 来计算最小香农熵,进而分析燃烧的特征时间.

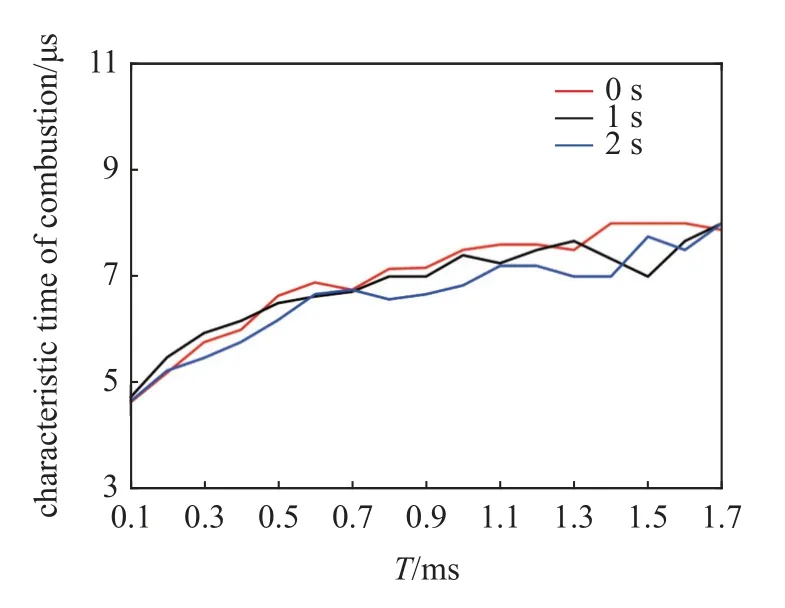
图16 采样时长的敏感性分析Fig.16 Sensitivity analysis of sampling duration

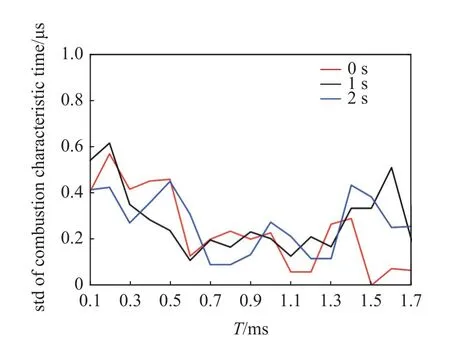
图17 采样时长敏感性变化的标准差分析Fig.17 Standard deviation analysis of sensitivity variation in sampling duration

3 实验结果

3.1 燃烧特征时间

首先通过燃烧自发光信号强度,定性观察火焰质心位置分布情况,如图18 所示.虽然燃料喷孔、凹腔等燃烧室内几何尺寸均为对称关系,但火焰质心分布极不规则,这是因为在超声速燃烧过程中受湍流场的影响,导致火焰质心呈现一定随机分布情况.而火焰质心的不均匀分布会导致不同位置燃烧速度存在差异,靠近火焰质心的位置,燃烧相对更强,化学反应速率更快.而更强的燃烧释热又会反作用于该处湍流场,使得湍流与燃烧之间存在多尺度强耦合作用,最终导致超声速湍流燃烧系统极其复杂,多种效应之间的解耦极其困难.虽然对超声速湍流燃烧机理的解析尚未能有详细完备的理论分析,但通过分析燃烧的特征时间,结合分区燃烧理论等,可以对不同马赫数下火焰分区进行判别,进而简化湍流燃烧问题,分析控制流动与燃烧的主导因素,得出相互作用机理.

图19 表示工况1 四个测点燃烧特征时间变化情况.首先可以发现,不同位置燃烧特征时间均在一定范围内小幅度波动,说明此时燃烧与输运呈现动态平衡,在该工况燃烧较为稳定.与图18 中火焰质心分布对比可知,随着火焰质心的靠近,测点P2 和测点P3 的燃烧特征时间会减小,距离质心越近化学反应速率越快.如图20 所示,从燃烧特征时间变化的标准差情况分析可知,质心靠近,燃烧特征时间的波动会相对减弱,主要是因为距离质心越近,燃烧相对更强,受到湍流场影响导致的燃烧强度变化相对更小,所以质心更近的位置燃烧波动更小.

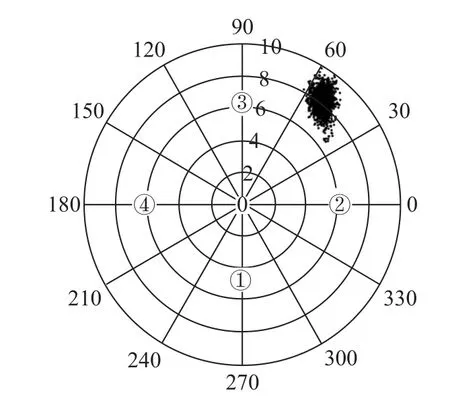
图18 工况1 中火焰质心位置分布Fig.18 Distribution of flame centroid position in condition 1

图19 工况1 下不同测点燃烧特征时间Fig.19 Combustion characteristic time of different points under condition 1

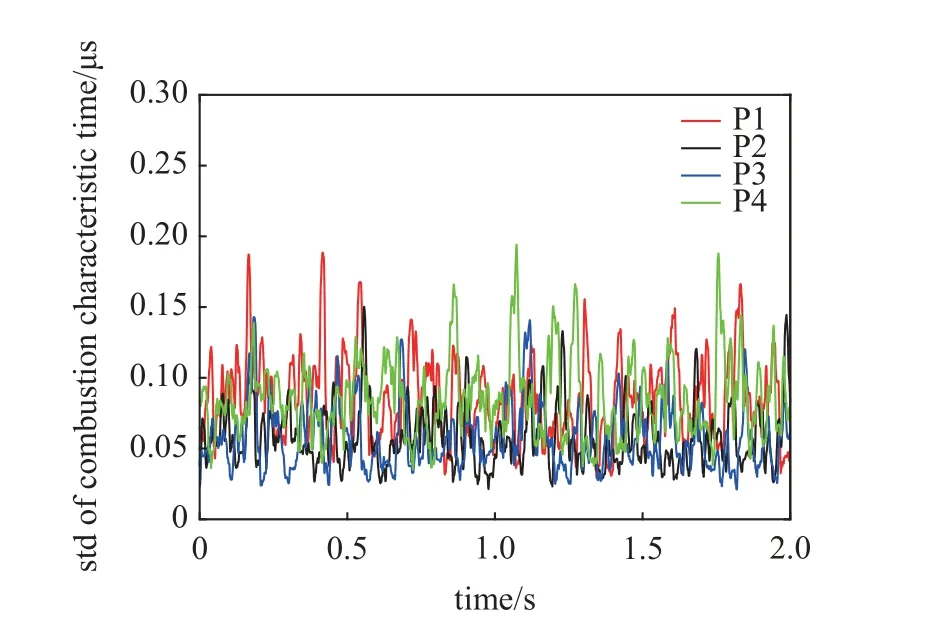
图20 工况1 下不同测点燃烧特征时间标准差Fig.20 Combustion characteristic time standard deviation at different points under condition 1

综上可知,火焰质心位置分布的定性观察与由最小香农熵计算得到的燃烧特征时间定量描述表征了相同的物理化学过程,进一步交互验证说明了实验方法的正确性.

3.2 当量比的影响

在实际的超燃冲压发动机工作中,由于混合效率不高,燃烧室内各处的局部当量比差异比较大,即存在贫燃区与富燃区共存的情况,局部当量比的分布特征影响燃烧效率、热释放率以及发动机的整体推力等性能.因此在来流总温总压以及马赫数不变的前提下,通过改变燃料喷注压力来对比不同当量比情况下燃烧特征时间的变化情况.如图21 所示为不同当量比情况下火焰质心的分布情况.由上一节分析可知,受到湍流场的影响,火焰质心分布呈现出一定随机变化,而对比不同当量比火焰质心位置分布情况可知,不同的燃烧模态同样也会对质心有所影响.图中当量比为0.13 时,火焰质心位置存在突变的情况,主要由于该工况处于模态转换阶段,不同的燃烧模态湍流与燃烧相互作用关系会有所改变,因此出现燃烧强度突变的情况,进而影响凹腔内火焰分布情况.

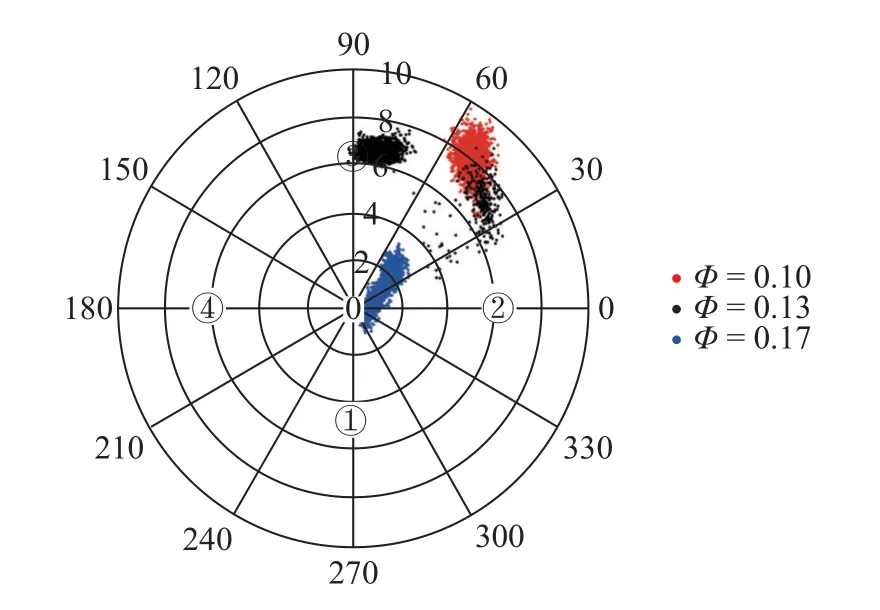
图21 不同当量比下火焰质心分布Fig.21 Flame centroid distribution of different stoichiometric ratios

如图22 和图23 所示为四个测点处不同当量比下燃烧特征时间均值以及相应的标准差变化情况.随着当量比的增加,燃烧特征时间呈现减小的趋势,化学反应速率加快,燃烧相对更强.并且由0.13 当量比燃烧特征时间变化情况可知,燃烧特征时间除与当量比有关以外,所处燃烧模态影响很大.在同为0.13 当量比的情况下,前半段的超燃模态燃烧特征时间明显高于后半段的亚燃模态的特征时间,并且两种燃烧模态下的燃烧特征时间分别与0.10 和0.17 当量比情况的特征时间近似.此外在当量比为0.10 和0.13 时,燃烧特征时间标准差普遍比当量比0.17 时更大并且会呈现出更剧烈波动的情况,说明Φ=0.17时燃烧更稳定.分析原因,主要是在较低当量比时火焰面较厚,通过下一节分析可知,比泰勒尺度更大,导致输运现象不仅受分子扩散控制,还受到湍流脉动的强烈影响,特别是大涡的卷吸和扭曲作用,使得当量比越大局部当量比也会随之升高,燃烧加强,燃烧特征时间变短.与此同时,湍流场涡结构会显著影响火焰面的形状和燃烧速度,大涡可以将火焰头部卷起,形成较为充分的多层,这不仅会影响燃烧强度,更会对燃烧中化学反应过程产生波动,相比较而言,在一定当量比范围内,燃烧越强,波动会越小.图中 Φ=0.13 工况之所以前半段会出现与Φ=0.10工况近似大小的特征时间以及波动情况,主要是由于该工况处于模态转换阶段,前半段处于与Φ=0.10工况相似的超燃模态,并且很快出现模态转换阶段,此时燃烧不稳定,热壅塞的出现最终导致燃烧强度突变等情况.

图22 不同当量比下燃烧特征时间Fig.22 Combustion characteristic time of different stoichiometric ratios

图23 不同当量比下燃烧特征时间标准差Fig.23 Combustion characteristic time standard deviation of different stoichiometric ratios

3.3 通量比的影响

除当量比以外,动量通量比也是目前较为关注的参数.因此,保持来流总温总压以及马赫数不变的前提下,通过改变燃料喷口孔径来对比不同通量比情况下燃烧特征时间的变化情况.

如图24 所示,工况3 与工况4 由于动量通量比近似,所以火焰质心分布较为相似,均在中心区域附近.而工况5 动量通量比减小,火焰质心出现突变情况,可能与稳焰分区分岔有关.

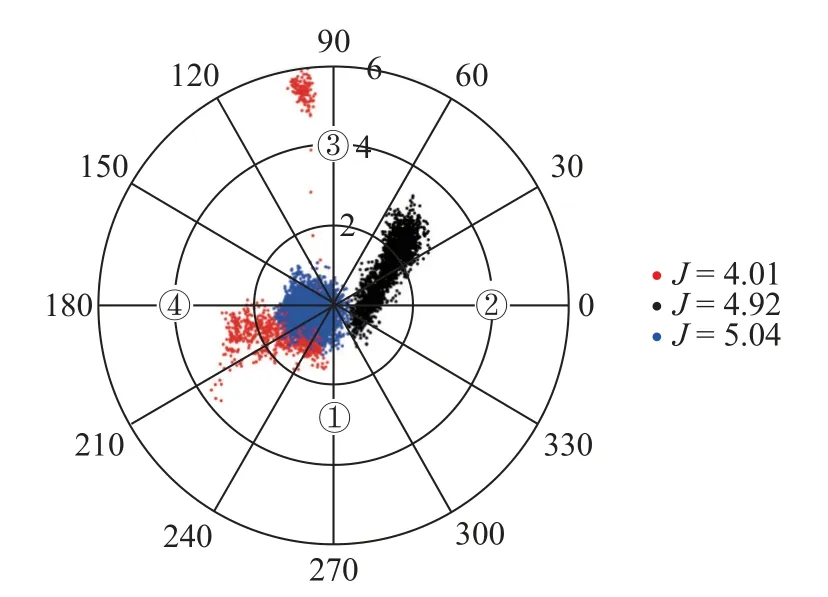
图24 不同通量比下火焰质心位置分布Fig.24 Distribution of flame centroid positions with different momentum flux ratios

如图25 所示为不同动量通量比下燃烧特征时间平均变化情况,随着动量通量比的增加,燃烧特征时间呈现出先减小后增大的趋势.与改变当量比相比,通量比改变对燃烧特征时间的影响较小,三种通量比的燃烧特征时间逐渐趋于一致.J=4.01 与J=5.04两种通量比的燃烧特征时间几乎相同,说明通量比对于燃烧结果的影响有限,存在极值.对比当量比变化的作用结果可知,通量比的改变导致的燃烧特征时间变化更小.此外,由图26 可知,相比较于改变当量比,通量比改变的三种工况燃烧特征时间的波动情况更接近.说明当量比对湍流燃烧影响更直接,而不同的通量比虽然会引起射流尺度等的变化,但最终对局部当量比的影响没有总当量比带来的改变大,甚至随着乙烯燃料的逐渐加入,三种通量比燃烧特征时间变化情况趋于一致.

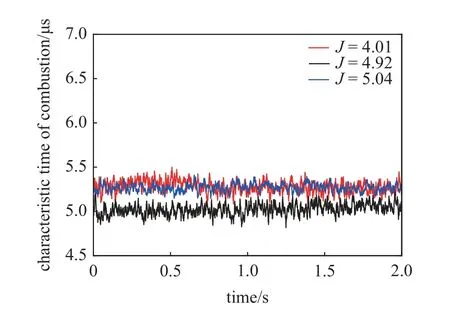
图25 不同通量比下燃烧特征时间Fig.25 Combustion characteristic time of different momentum flux ratios

图26 不同通量比下燃烧特征时间标准差Fig.26 Combustion characteristic time standard deviation of different momentum flux ratios

3.4 马赫数的影响

超燃冲压发动机在实际飞行过程中存在加速过程,除当量比、通量比等变化情况以外,还存在马赫数变化的宽域飞行需求.加速上行结果如图27 所示,加速上行过程中,燃烧室内火焰质心分布情况相对较稳定,并未随着马赫数的变化而出现剧烈变化,均集中在P3 测点附近.如图28 和图29 所示加速上行过程中4 个测点位置及其均值的燃烧特征时间变化情况.由图可知,随着马赫数的增加,前3.5 s 内燃烧特征时间较为稳定,在3.5 s 以后开始出现减小的趋势,说明此时燃烧逐渐增强,特别是靠近火焰质心的P3 测点位置,特征时间变化更为明显.

图27 加速上行实验火焰质心的分布Fig.27 Distribution of flame centroid positions with acceleration

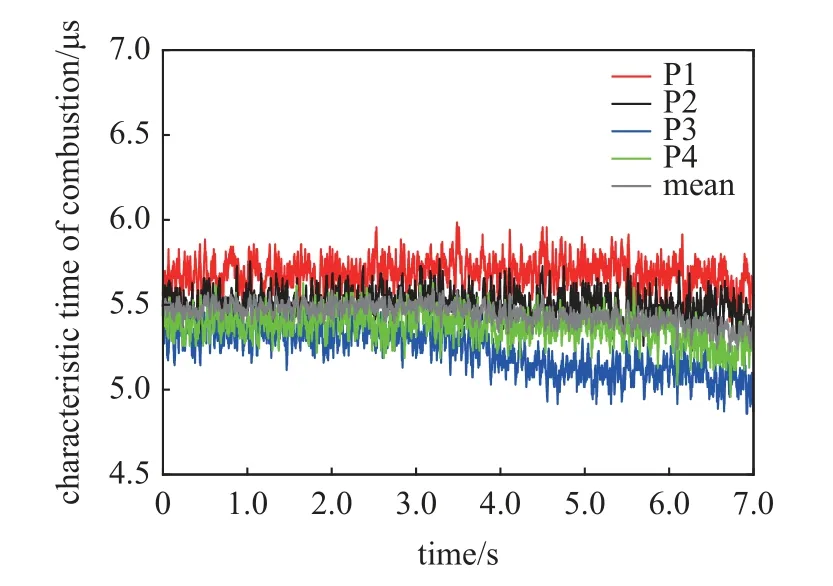
图28 加速上行实验不同测点的燃烧特征时间Fig.28 Combustion characteristic time of different points under acceleration experiment

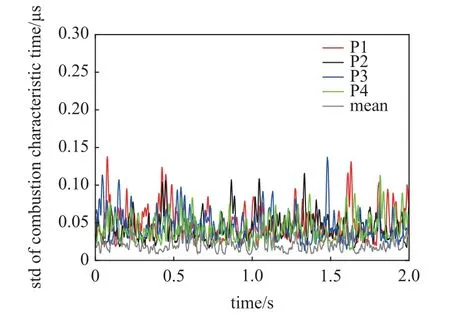
图29 加速上行实验不同测点燃烧特征时间标准差Fig.29 Combustion characteristic time standard deviation at different points under acceleration experiment

虽然加速上行实验中,马赫数和通量比与改变当量比实验中相应参数不同,但加速上行实验中当量比从0.10 变化到0.13 的前3.5 s 过程中燃烧特征时间变化较小,而当量比从0.13 变化到0.17 时燃烧特征时间逐渐减小,该结果刚好与上述改变当量比定常实验结果相吻合,说明当量比的变化所带来的影响更为明显.与此同时,对比改变当量比的定常实验可知,虽然同样当量比变化范围均在0.10～0.17 范围内,但马赫数的动态变化导致在加速上行实验过程中并未出现超燃与亚燃模态的转换,均为亚燃模态,这与改变当量比的定常实验有所不同.说明马赫数变化所导致的流场以及释热的变化避免了热壅塞的出现,详细机理需要具体分析此时流场以及释热等的变化情况才能加以说明.但从下一节分析可知,随着马赫数的增加,丹姆克尔数逐渐减小,大尺度涡结构带来的影响增强,使得燃烧室内混合与燃烧过程受到湍流影响逐渐增加,进而两者之间相互作用加深,整个燃烧室内的释热情况有别于改变当量比的定常实验,从而避免了热壅塞的出现.

3.5 发动机工作范围

通过以上分析,首次从实验中估算了燃烧的特征时间tchem,作为湍流燃烧问题的研究基础,将根据以上结果结合分区燃烧等理论对超声速湍流燃烧火焰分区判别,进而分析湍流与燃烧相互作用过程中的主导因素,简化相互作用关系.

由第2 节介绍的火焰分区判别方法可知,需要计算流动特征时间tflow以及燃烧的特征时间tchem,其中燃烧的特征时间tchem由实验测得tchem=τsc,而流动特征时间可由来流条件结合相应理论估算得到,这也是目前较为常用的方式[31].

根据实验设计,定常实验超燃冲压发动机隔离段入口马赫数Ma=2.8,非定常实验超燃冲压发动机隔离段入口马赫数Ma=2.5 ∼2.8 ∼3.0，总温度T=1475 K .由Sutherland 公式[32]动力黏度 µ

其中,T为来流总温,µ0与B为实验参数,与气体种类有关.当为空气时,µ0=1.7894×10−5而B=110.4 K .因此,来流动力黏度 µ ≈5.21×10−5.之后根据绝热等熵流动基本关系

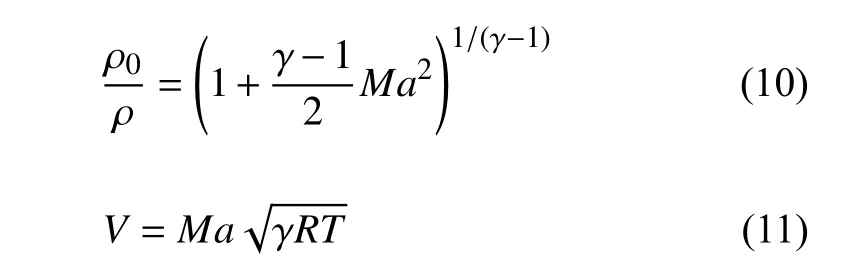
由此可得,定常实验来流的密度 ρ ≈1.30 kg/m3,以及来流速度V≈2159.31 m/s .而加速上行的非定常实验来流的密度 ρ ≈1.08∼1.84 kg/m3,来流速度V≈1927.95 ∼2313.54 m/s.

高速相机的传感器大小是1920×1080 像素,根据单像素点对应的真实长度计算得到,实验用高速空间分辨率是每像素107 μm,误差范围在107 μm,对比高精度数值模拟计算结果,高速空间分辨率约为2～3 倍Kolmogorov 尺度,根据实验流体力学领域常用的评估测量有效实验空间分辨率方法(<3η),基于高速纹影的流动参数估算方法具有一定的可信度.如图30 所示.

图30 超声速燃烧高速纹影图像Fig.30 High speed schlieren image of supersonic combustion

根据充分发展湍流的经验公式可知

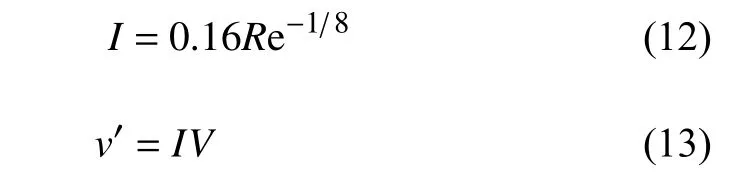
综上所述,根据燃烧室入口来流条件可以估算出以上五种定常实验工况下湍流的流动特征时间,约为tflow=L0/v′≈11.30 μs,而实验中测得的燃烧特征时间tchem=τsc=5.05 ∼5.80 μs,与式(2)联立可解出丹姆克尔数Da.将本次五种定常实验全部工况中有效时间内的所有丹姆克尔数整合后分析发现,Da≈2.00～ 2.40.而加速上行的非定常实验丹姆克尔数随着马赫数的增加变化情况约为Da≈ 1.80～ 2.60.全部工况的丹姆克尔数概率密度分布如图31 所示.

基于以上分析结果,在燃烧分区图上绘制出发动机此时工作范围,如图32 所示.图中红色区域为本次实验发动机工作范围,均在B 区域,此时火焰分区处于旋涡小火焰分区,燃烧状态受到湍流涡结构较大的影响.此外考虑可压缩性的影响,此时B 区域中快慢化学反应的分界线位于Da=2.20 位置,所以本次实验工况3 完全处于B 区域中的快速化学反应区域,工况6 的加速上行实验处于快慢化学反应交替出现的阶段,其余工况均处于泰勒尺度以下的慢速化学反应区域.该实验结果说明本次实验工况下的超声速燃烧受到湍流影响,并且该影响在较低当量比时主要来自于湍流大尺度涡结构的卷吸和扭曲作用,在较高的当量比并且中等通量比时,该影响来自于湍流中小尺度涡结构的脉动影响更大.而在加速上行实验中,由于马赫数逐渐增加,流动时间尺度受到较大影响,导致在整个实验有效时间内处于快慢速化学反应交替出现的情况,湍流场中不同尺度的涡结构分别作用于超声速燃烧过程.并且由图31可知,加速上行实验丹姆克尔数分布更均匀且在2.2 左右,同样说明此时流场变化对于燃烧情况的影响较大.

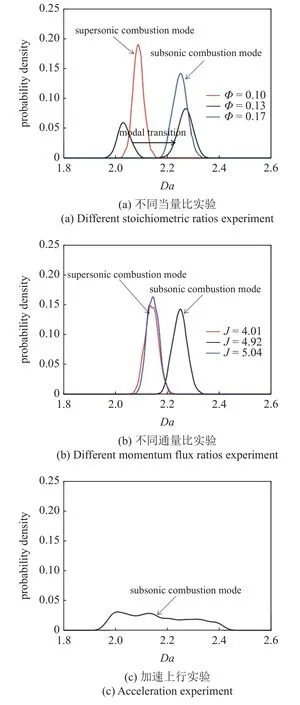
图31 全部工况的 D a 概率密度分布Fig.31 D a probability density distribution of all experiment conditions

图32 本次实验发动机工作范围Fig.32 Working range of the engine in these experiments

本文通过实验方法验证了超声速燃烧中湍流起到重要作用,并且可简化为大尺度涡结构卷吸与扭曲或者小尺度涡结构的脉动对于超声速燃烧的影响.在此基础上,根据实验中不同的燃烧分区情况,对湍流场进行简化.特别是对于以碳氢燃料为主的超燃冲压发动机,可具体根据快慢化学反应区域的不同,分别观测小尺度涡结构或者大尺度涡结构的衍化规律,进而分析湍流与燃烧相互作用的机理.本文报告的实验结果与文献[31]开展的碳氢燃料仿真结果基本一致.

4 结论

本文研究基于单边扩张双模态冲压发动机燃烧室模型,其有效当量比工作范围较窄,实验数据具有一定局限性.本文遍历了该模型由超燃工作模态到近热雍塞工作状态的燃料质量流量和一定的来流变化条件,当前研究表明碳氢燃料超声速燃烧在旋涡小火焰区域(B 区),多尺度湍流涡结构发挥重要作用,在宽域湍流燃烧研究中需要着重关注宽域来流和多尺度流动特性,具体得到了如下结论.CH∗

(1) 提出了一种基于内窥光纤传感器测量 自发光时间序列信号,通过最小香农熵“唯一解”定义燃烧特征时间的方法,并获得了不同燃料当量比、通量比、来流马赫数实验条件下的超声速燃烧特征时间.

(2) 在实验当量比的范围内,碳氢燃料超声速燃烧分区在旋涡小火焰区域(B 区),多尺度湍流涡结构发挥重要作用.当量比增加可导致燃烧特征时间减小,表现为超声速燃烧分区在旋涡小火焰区域上移,主导流动由较大尺度涡结构向小尺度湍流涡结构过渡.

(3) 在实验通量比的范围内,动量通量比对燃烧分区影响不大,但是动量通量比对碳氢燃料超声速燃烧特征时间及燃烧分区存在分岔现象.在中等通量比情况下出现了旋涡小火焰区域小尺度涡结构作用的情况.

(4) 加速上行实验说明,来流条件变化显著影响碳氢燃料超声速燃烧特征时间及燃烧分区,宽域来流影响作用机制是未来宽域湍流燃烧理论研究的重要方向.

附录

最小香农熵原理分析,参考Softmax 函数,其计算了不同类别之间的相对概率

式中,Vi是分类器前级输出单元的输出,nseq表示不同类型调查序列的总数.

香农熵

其中,Pk表示在时间调查窗口为L和符号分割数目N一定时,每组调查序列出现的概率.nseq 表示不同类型调查序列的总数.当香农熵Hs等于1 时,表示该系统完全随机;当香农熵Hs小于1,表示该系统存在确定性机制,香农熵越小确定性越强.而随着调查窗口L和符号分割数目N不同,Pk和nseq随之改变.对Hs求导分析,极小值存在的情况

由上式可知,随着Pk和nseq的不同,香农熵数值以及偏导数均在变化,针对某一时间序列的时间分析,当调查窗口L和符号分割数目N与真实规律偏离较大时,事件中包含的每种类别的概率Pi极低,此时香农熵较大,偏导数小于0,香农熵递减.而当接近真实规律时,事件确定性逐渐加强,所有类别的概率中便会出现某些显著高于其他类别的概率,该结果在实验数据分析过程中已有验证.最终导致香农熵值逐渐减小,偏导数此时逐渐由负转正,即出现极小值点,并且此时对应的调查窗口L和符号分割数目N便是接近于该时间序列内在规律的划分情况,而时间调查窗口即对应此时的特征时间.

综上所述,越接近真实特征时间的调查窗口L,其划分出的各种类别的事件会有部分事件重复出现多次,其概率会集中于此部分事件,导致偏导数由负转正,因此,燃烧自发光信号的香农熵极小值点所对应的调查窗口L是唯一解,可以用来代表燃烧特征时间.