Matlab在三重积分计算的教学设计中的可视化应用

张 凤 田 祥＊ 朱柘琍

（山东农业大学信息学院，山东 泰安 271018）

0 引言

三重积分的计算需要学生有很强的空间想象力和运算能力，学生在学习的过程中可能会觉得烦躁，产生厌烦情绪，这不利于高等数学教学工作的开展。那么如何让抽象的概念变得直观形象，让复杂的计算迎刃而解，增加学生学习高等数学的信心和兴趣呢？笔者在教学设计环节上狠下功夫，首先通过引入环节让学生意识到学习三重积分的意义和作用，接着在具体的讲解计算方法的过程中通过一只土豆的质量切丁、切丝还是切片生动形象地把三重积分的计算问题化解为先一后二或先二后一，最后在教学实例中运用数学软件作为辅助，实现积分区域的可视化，并用Matlab程序语言快速实现累次积分的计算，让学生体会到将数学和计算机双剑合璧的力量，改变了传统的教学模式，提高了教学的效率。

1 教学设计的引入环节

也就是说一个土豆，密度不均匀，要求土豆的质量，就切丁，通过切丁法我们就将土豆的质量转化成了三重积分。通过以上讨论知道要求不规则物体的质量就是以密度函数为被积函数在相应区域上做三重积分。但是同学会问三重积分该怎么计算呢？笔者的思路是把三重积分化成三次积分，也就是三个定积分，然后应用N-L公式就解决了。但是如何将三重积分转化成三个定积分呢？那就要看这个土豆，也就是积分区域的形状了。在直角坐标系下，理论上的方法有两个：一是先一后二法，也叫投影法，形象一点叫切丝法；二是先二后一法，也叫截面法或切片法。下面先来看怎么切丝。

2 投影法（先一后二法或切丝法）

2.1 区域为X-Y型

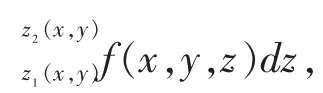
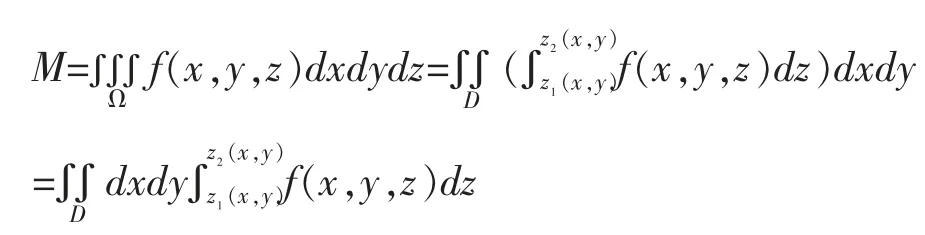
通过以上的讨论，区域为X-Y型的三重积分方法为：

（1）画出积分区域图；（2）判断积分区域的类型；（3）选择合适的积分次序，在这里强调当是X-Y型区域就是先对z积分；（4）确定积分限。

确定积分内限的口诀为：域内一线穿，两点定内限；积分区域既然有X-Y型区域就有X-Z型区域或者Y-Z型，所以很自然的引入X-Z型区域。

2.2 区域为X-Y型区域

在这里强调当土豆是X-Z型区域时，要向xoz面投影，从而先对y积分，并且确定积分限的口诀仍然适用，即此时土豆的质量为：

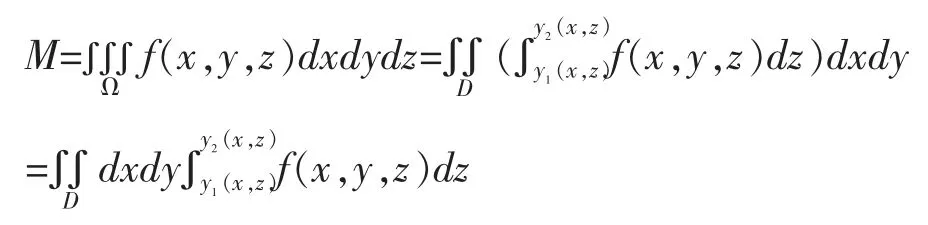
讲完了以上两种类型，Y-Z型不再赘述。下面来讨论截面法也就是先二后一法或者切片法。什么时候适合切片呢？就是当土豆的密度也就是被积函数是关于z的一元函数的时候。

3 截面法

（假设被积函数是关于z的一元函数，即土豆的密度为f（z））

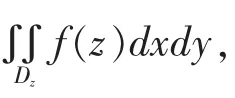
通过以上的讨论，什么样的类型适合用截面法总结如下：

（1）被积函数是关于z的一元函数；（2）截面的形状规则，面积好算。

思考一下，如果被积函数是关于x的一元函数呢？该怎么切片？大家可以自行给出结果。最后强调一下，在直角坐标系下，以上的方法同样适用于被积函数符号任意的情形。下面看具体的例子。

4 例题

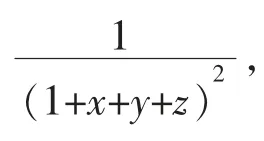
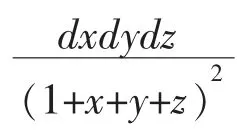
绘制的图形如图1所示

图1 四面体

四面体Ω可以看作是X-Y型区域，向xoy面投影，投影域D为（见图2）。应用投影法，三重积分可化为：

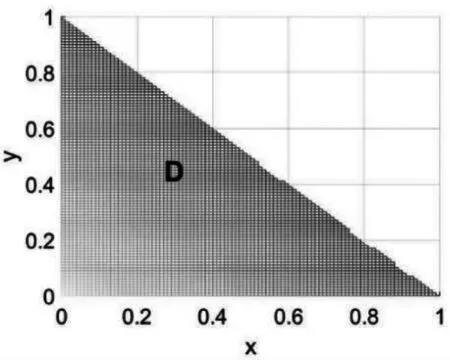
图2 投影域

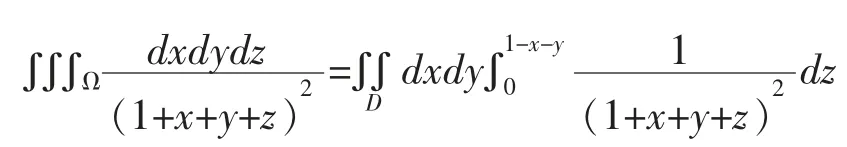
同学们看到了这个积分肯定打退堂鼓，因为积分的计算量比较大了。没关系，接着让计算机计算，用Matlab编程如下：

所以学会了三重积分化累次积分之后，具体的累次积分计算的实现过程完全可以借助计算机。

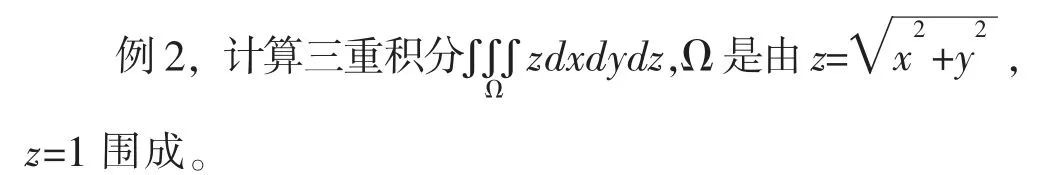
分析：积分区域Ω上是一个上半锥，像甜筒，先应用Matlab程序语言将它的图形绘制出来，程序如下：

绘制图形如图3所示。

图3 积分区域

这个三重积分被积函数是关于z的一元函数，积分区域的截面（见图4）都是圆，所以适合切片，因而应用截面法就将三重积分化为：

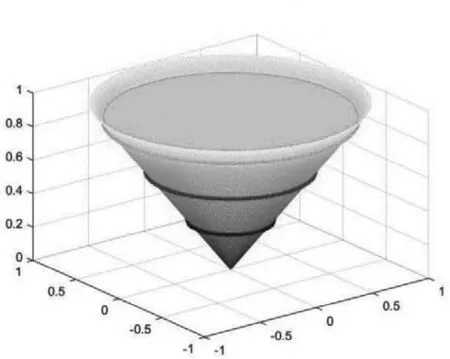
图4 积分区域的截面

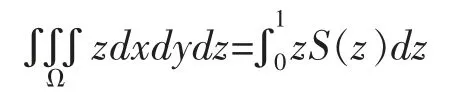
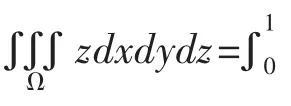
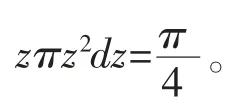
不由得感慨，so easy！这其实就是方法选对了，所以事半功倍。

5 结语

在高等数学中，三重积分的计算是难点更是重点，它需要扎实的计算能力以及空间的想象力，让学生们望而生畏，望而却步，所以笔者在三重积分计算的程序设计中引入了Matlab。Matlab具有强大的符号计算功能以及图形绘制功能，将Matlab引入高等数学的课堂改变了传统的粉笔加黑板的课堂教学模式，可以很方便地将一些抽象的函数形象的表示出来，给学生更直观的讲述效果，进而加深学生对教学内容的理解，使高等数学不再晦涩难懂。Matlab程序设计的介入提高了学生的空间想象力，也增加了学生自主学习高等数学的兴趣，是培养学生数学素养的有力工具。