小积木，大秘密

李婉悠

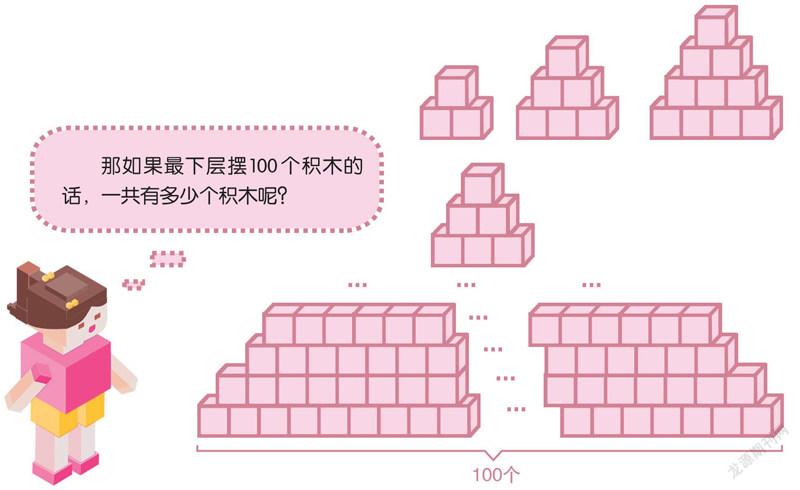
小时候，我很喜欢用积木玩搭房子游戏，于是爸爸妈妈给我买了各种各样的积木。随着年龄的增长，我的爱好越来越广泛，小小的积木被我遗忘在玩具箱的一角，渐渐地落上了灰尘。

炎炎夏日，我不得不“宅”在家里。一天下午，我闲来无事，不经意间看到了一盒积木，就顺手玩了起来。玩着玩着，我突然想到：如果把积木摆成每个下层都比上层多1个的话，会怎么样呢？

最下层摆2个，一共有1+2=3（个）;

最下层摆3个，一共有1+2+3=6（个）;

最下层摆4个，一共有1+2+3+4=10（个）。

根据我刚刚发现的规律，积木的总数量就得从1一直加到100了，列算式为：100+99+98+

97+…+2+1，这样一个一个地加下去也太麻烦了！有没有更简单的计算方法呢？

仔细观察这个算式，我发现99+1=100，98+2=100，97+3=100……从1一直加到100，能凑够多少个100呢？我想了想，1～100一共有100个数，除了100与50不用凑整外，还剩下98个数。每两个数可以凑成1个100，那么一共就有98÷2=49（个）。再加上100和50，积木的数量就是49×100+100+50=5050（个）。

当我把自己的想法告诉爸爸时，他直夸我會思考，然后摸着我的头，说道：“我们都习惯凑整十、整百、整千等十的倍数。我们突破一下这种思维，1～100共100个数，如果两两凑对，凑成50对，又会怎么样呢？”在爸爸的提示下，我恍然大悟：“我明白了！1+100=101，2+99=101……直到50+51=101，就有50个101，也就是5050！”

“这样首尾配对的计算方法更加简便，太不可思议了！”我蹦蹦跳跳地去和妈妈分享了我的发现。“悠悠，你真了不起，竟然和数学家高斯用的方法一样！”妈妈高兴地说道，“这种首尾凑对的方法，又被人们称作‘高斯求和’！”

听着妈妈的介绍，我陷入沉思：除了高斯的方法，还有没有其他思路呢？远远望去，我发现自己搭的积木就像一个个“梯形”骄傲地站在那儿。突然，之前妈妈说过的“梯形的面积=（上底+下底）×高÷2”在我脑海中闪现。

于是，我开始了新的尝试。我把最上层的积木当作梯形的“上底”，最下层的积木当作梯形的“下底”，积木的层数当作梯形的“高”，所以一共有（100+1）×100÷2=5050（个）积木。

“妈妈，谢谢您，我发现这个问题也可以用您以前告诉我的梯形面积公式解决！”我抑制不住内心的激动，冲上去一把抱住了妈妈。

我闭上眼睛，静静地享受着小小积木中蕴藏的“大秘密”。原来，只要拥有数学的思维方式，即使是玩积木，也可以让我体会到思考的乐趣。我真是太开心啦！

个人档

710062 陕西省西安市陕西师范大学附属小学四（10）班

指导老师 白翠霞

刘彭旖  7月3日  14：59：01

看完婉悠的讲解后，我忍不住也玩起了搭积木，然后惊奇地发现，摆成每个下层都比上层多同样数量的积木时，得到的图形都是梯形！这就意味着婉悠总结出的公式，也能用在这些情况的计算中。

豆悦熙  7月3日  15：14：24

这个我在课外书上看到过，高斯求和公式又叫等差数列求和公式。若两两相邻的积木数量之差都相等，则由每层积木的数量构成的数列就叫等差数列，比如3，5，7，9……婉悠能自己想出来真的很厉害啊！

谢雨珂  7月3日  18：21：30

数学的探索真是无穷无尽，稍一松懈，说不定就会有一个数学定理从手边溜走了。听说等差数列还有个“兄弟”叫等比数列，我也要加把劲，好好“闭关”钻研一下。