基于核方法与流形学习的运动想象脑电信号特征提取算法*
祝 磊朱洁萍丁旺盼杨君婷胡奇峰应南娇徐 平张建海
(1.杭州电子科技大学自动化学院,浙江 杭州 310018;2.杭州电子科技大学计算机学院,浙江 杭州 310018;3.浙江省脑机协同智能重点实验室,浙江 杭州 310018)
脑机接口(Brain-computer Interface,BCI)是将大脑活动通过信号采集系统进行记录并分析从而实现计算机与大脑连接[1]的技术。 近年来,BCI 技术在临床领域应用广泛[2],用于病患的身体康复[3]以及行为活动的辅助[4]。 BCI 技术应用的关键在于脑电信号的特征提取以及分类模型的构建[5]。 并非所有从EEG 信号中提取的特征都与分类相关。 过多的特征不仅会增加特征矩阵的维数,还会导致分类成功率低[6]。 因而解决高维数据造成的计算复杂度高和分类精度低的问题[7]至关重要。
包括独立成分分析[8](Independent Component Analysis,ICA)、主成分分析[9](Principal Component Analysis, PCA) 和线性判别分析[10]( Linear Discriminant Analysis,LDA)等在内的降维算法在传统BCI 中得到广泛应用,但大都忽略了脑电信号中重要的结构信息。 共空间模式(Common Spatial Pattern,CSP)算法从多通道的数据中提取出每一类的空间分布成分,能很好地利用脑电信号的空间相关性,并且对于信号的噪声也有着很好的消除效果,表现出较好的分类性能[11-12],被认为是最流行的运动想象应用技术[13],但是却强烈依赖于频带的选择[14]。 此外,流形学习也被用于运动想象脑电的研究中,如Li 等[15]使用了局部线性嵌入(Locally Linear Embedding,LLE)算法提取运动想象脑电中的非线性特征,并获得了较高的分类精度。 但考虑到脑电信号并不是单纯向量化的数据,单纯使用基于向量的特征提取方法会造成空间信息的丢失。Hu 等[16]提出了一种基于矩阵变量高斯模型的双线性二维判别局部保持投影(B2DDLPP)算法,在二维判别局部保持投影(2DDLPP)算法[17]中引入双线性结构和矩阵变量高斯模型,来充分提取EEG 信号通道之间的特征信息,获得了较好的判别性能。
针对脑电信号中的非线性特点,本文引入核函数的方法以加强对数据特征的获取,并结合双向二维判别局部保留投影算法,提出一种核-双向二维判别局部保留投影(Kernel Bilinear Two-dimensional Discriminant Locality Preserving Projection, Kernel-B2DDLPP)算法来进行特征提取。 通过将数据映射到合适的高维空间,使得线性不可分的脑电数据在高维空间中的特征更加具有区分性。 并在预处理阶段参考滤波器组共空间模式(FBCSP)算法[18],将EEG 信号过滤成多个频带,从每一个频带的数据中提取出CSP 特征,整合生成频-空矩阵集作为特征提取步骤的输入。 最后使用了支持向量机(SVM)[19]对提取的特征值进行分类。 实验结果表明,该方法有效地保留了更高精度的数据特征,具有较好的分类稳定性,提高了分类正确率。
1 特征提取方法
1.1 流形学习方法
二维判别局部保留投影(2DDLPP)算法是DLPP算法的2D 拓展,可以将样本中的空间结构信息考虑在内,提供更高精度的样本近似。 B2DDLPP 算法基于矩阵变量高斯模型,对2DDLPP 算法进行了改进。
假设每一个样本的特征矩阵X的大小为Nf×Ng,总样本数为N,每一个类别中的样本数ns,类别s=1,2,…Z,类别对应的矩阵集为第s个类别中的样本个数。 原始空间RD中的样本X=(x1,x2,…,xN),要找到一个投影矩阵,将样本集投影到一个低维的空间Rd,并保留原始空间中的邻域关系,投影后的样本集记为Y=(y1,y2,…,yN)。 B2DDLPP 的目标函数为:

式中:G为目标投影方向,SB是类间散布矩阵,SW是类内散布矩阵。
通过最大化目标函数获得投影方向,并对相应的协方差矩阵进行近似:

式中:ψ、ϕ分别表示空间协方差矩阵和频率协方差矩阵。Ws是同类别中任意两个样本之间的权值,定义为
B2DDLPP 算法定义向量化后的类间散布矩阵是一个可分离结构,SB=SBR⊗SBL,表达式分别为:

式中:u为F的向量化,u=vec(F),Fs为s类别的样本均值矩阵。Bab是任意两个类别样本均值之间的权值矩阵,定义为Bab=exp(-‖Fa-Fb‖2t)。
可以得到ϕ-1SBL的特征值和特征向量,分别记为λl和ul。 类似的,可以得到ψ-1SBR的特征值和特征向量,记为γj和vj。 接着将特征值λl和γj分别进行降序排列,对应的特征向量进行重构,得到投影矩阵U、V。 特征矩阵Y可以通过Y=UTXV得到。
1.2 核方法
一个非线性函数进行显式的映射会带来非常大的计算量,并引起维数灾难。 通过核函数计算高维空间中向量的内积,使‹ϕ(x),ϕ(y)›=K(x,y),即可解决上述问题。
将原始空间内的样本按列进行分块,可得Xi=[α1,α2,…,αn]。 根据核方法的理论,存在一个非线性映射ϕ,将原始空间里的脑电样本映射到核空间中X→ϕ(X)。 可得核矩阵K具体形式如下:

1.3 核-双向二维判别局部保留投影算法
本文在B2DDLPP[16]基础上引入了核方法的思想,将权值矩阵和样本进行了非线性拓展,提出一种核-双向二维判别局部保留投影算法(Kernel-B2DDLPP),以得到更具有判别力的特征。
根据B2DDLPP 中的理论,类内散布矩阵SW和类间散布矩阵SB都可进行拆分两部分,SW拆分成SWL和SWR如下:
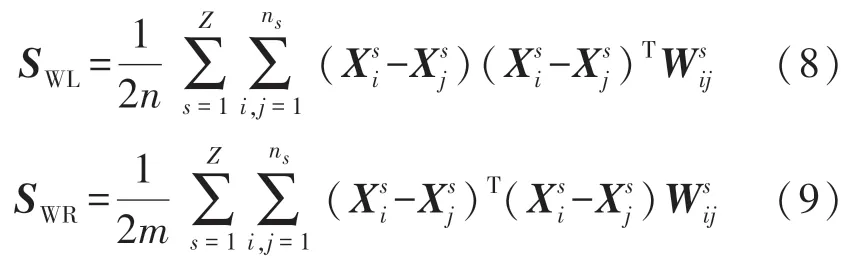
SB拆分成SBL和SBR,如下:

以SWL和SBL部分为例,通过非线性映射后,对应在核空间的类内散布矩阵和类间散布矩阵转换成:

目标函数为:

根据再生核理论,可以令W=ϕ(X)Γ,将目标函数进行转换。 分子部分转换成:

分母部分转换成:
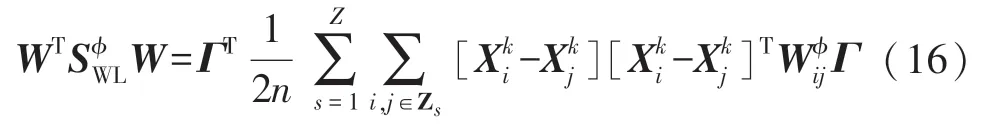
和需要转换成核空间内的权值矩阵,由于在核空间内的样本形式未知,因此本文也利用了核函数的方法,运算中的内积用核函数来进行替代,进行求解。 以类内散布矩阵中两个样本矩阵ϕ(Xi)和ϕ(Xj)之间的权重为例:

相当于以作为新的样本,i=1,2,…,N。 随后求解出列的投影矩阵V。
以类似步骤,进行SWR和SBR部分的计算。 与上部分不同的是,输入的X按行进行分块,核矩阵K大小相应地变成mN×mN,为一个mN×m的矩阵,i=1,2,…N。 最终可以计算出该部分按行的投影矩阵U。
计算新的样本以及权值矩阵得到一个方向的投影矩阵,应用于原始样本X。 结合B2DDLPP 的特征选择的思想,从特征矩阵Y=UTXV中挑选出前d个最大的λlγj值所对应的yij元素,作为降维后的d维特征。
2 实验数据
实验使用两个公开数据集进行对比试验,均为四分类运动想象BCI 竞赛公开数据集,分别是BCI Competition 4 的Dataset 2a[20]以及BCI Competition 3的Dataset 3a[21]。
两个公开数据集均为左右手、脚和舌头的四分类运动想象数据。 其中Dataset 2a 数据集的信号通过布满头皮的22个电极进行采集,每个电极以250 Hz 的采样频率收集信号,并在0.5 Hz~100 Hz 直接进行带通滤波。 该数据集总共包含9 名受试者,Dataset 3a 数据集包括3 名受试者,通过60个通道的电极以250 Hz 的采样频率进行采样,并且通过陷波滤波器进行1 Hz~50 Hz 滤波。 二者的实验范式分别如图1 和图2 所示。

图1 竞赛数据集Dataset 2a 的实验范式图

图2 竞赛数据集Dataset 3a 的实验范式图
为了更好地保留空间结构信息,本文实验使用了数据集的所有电极通道的数据。
3 实验结果与分析
3.1 预处理
考虑到CSP 算法的表现十分依赖于脑电信号中的最优频带,且运动想象信息主要包含在μ 频段(8 Hz~13 Hz)和β 频段(14 Hz~0 Hz)中,而眼电噪声频率范围主要存在较低频中,因此预处理部分参考滤波器组共空间模式(FBCSP)采用了一个覆盖4 Hz~40 Hz 的切比雪夫Ⅱ型滤波器组将所有脑电信号划分为多个子频段,每4 Hz 频段进行一个分割,共划分为9个子频段,各子频带的频率范围在表1 中列出。

表1 滤波器组划分脑电信号对应各频段频率范围
3.2 特征提取分类
首先将经预处理后得到的九个频段数据采用一对多共空间模式算法(one versus the rest common spatial patterns,OVR-CSP)进行第一阶段的特征提取,得到一组频-空特征数据集。 对于四分类数据,总共可以得到四组特征。 将得到的Z组特征组合起来,Z为总类数,最后得到一个大小为Nf×Ng的特征矩阵,其中Nf为划分的频带数,Ng=2pZ,p为CSP算法中计算投影矩阵时的特征向量选取数目参数。
再将特征集XNf×Ng通过核-双向二维判别局部保留投影算法进行第二阶段特征提取,构造投影矩阵U,V,计算特征矩阵Y,从Y中挑选出前d个最大的λlγj值所对应的ylj元素作为降维后的特征维数。
最后将降维后的特征集使用SVM 分类器进行分类,根据分类结果分析性能。
算法的性能取决于分类器输入的特征空间的维数,用d表示,而d的取值范围受第一阶段特征提取部分参数p的影响。 考虑到脑电数据在不同数据集中、不同受试上的各异性,且计算量将随p值的增加而增大,本文将实验中参数p的取值范围选定为[1,4]。 对于每一种特征提取的方法,根据每个受试者5 折交叉验证的平均结果来确定最优维数dop。测试集数据用训练得到的最优维数进行降维。 实验的总体流程图如图3 所示。

图3 本文实验总体流程图
3.3 结果与讨论
实验将本文算法与五种算法进行分类结果对比。其中,对比CSP 算法是为了验证流形学习方法的加入对特征空间描述信息补足的积极作用,对比CSP+B2DDLPP 算法用于验证核方法对非线性特性处理脑电信号数据的有效性。 KPCA[22]、KLDA[23]、KLPP[24]作为常用的核降维算法也与本文算法进行了对比。需要说明的是,初步实验中,算法使用的核函数均为高斯核函数(RBF),函数中的参数σ2设置为1,B2DDLPP 算法以及本文算法中进行权重矩阵计算时的参数t设置为1。 Dataset 2a 数据集与Dataset 3a 数据集的具体验证结果分别由表2 和表3 所示。

表2 Dataset 3a 数据集中不同特征提取算法的最佳交叉验证结果

表3 Dataset 2a 数据集中不同特征提取算法的最佳交叉验证结果
可以看出,在两个不同数据集中,整体上本文改进后算法的分类结果都优于其余五种算法,相比加入B2DDLPP 算法有小幅度提升,而对比于其余四种算法,本文算法均表现出明显的优越性。 如表3和表4 所示,在数据集Dataset 3a 上,其平均分类精确度相较于CSP、CSP +B2DDLPP、CSP +KPCA、CSP+KLPP 以及CSP +KLDA 五种算法分别提升了4.71%、4.44%、6.85%、11.67%及9.08%;在数据集Dataset 2a 上,也分别提升了10.89%、2.1%、5.2%、11.12%及11.11%。 从单个受试者的分类结果来看,本文算法对分类性能的提升在数据集Dataset 3a 上表现得更为明显,且相比其他算法均有很大提升。与应用B2DDLPP 算法相比,除2A06 受试者的分类精度增加了16.27%之外,2A02、2A04 受试者的分类精确度有少许降低,但差距很小,大部分受试者的分类精度均有小幅度提升。 这足以证明处理脑电信号时考虑数据中存在的非线性关系意义重大。
相比于其他五种算法,仅使用CSP 算法的分类结果波动较大,在受试者2A02 和2A06 上表现出较高的分类性能,而在其余受试者的数据上表现不佳。这可能是由于本文实验为了确保通道结构的完整性,使用了所有采集通道的数据,这带来了冗余的数据和噪声,而CSP 算法对数据预处理的要求很高,对于噪声的鲁棒性较差。 相比于B2DDLPP 方法,本文算法通过引入核函数加强了对数据非线性特征的提取能力,在处理脑电数据上的表现有了一定程度的提升。 KPCA、KLPP 以及KLDA 算法虽然为非线性特征提取方法,但在实验中的分类性能表现均不理想,这是由于这类向量化特征提取方法会在一定程度上造成空间信息的丢失,破坏了数据的结构特征,使得提取后的特征区分度降低,从而导致最终的分类准确率不佳。
图4、图5 及图6 分别为样本原始特征、样本特征经FBCSP 预处理后以及样本特征由本文算法提取后的特征值分布。 可以直观地看出,经FBCSP 处理后特征有一定区分度但仍有较多重叠,而经过本文方法进行特征提取后,左手、右手及舌头样本特征几乎可以完全区分,足部特征的区分度也有了较大提升。

图4 原始样本特征分布

图5 FBCSP 预处理后样本特征分布

图6 本文算法特征提取后样本特征分布
值得注意的是,分类精度在一定程度上受输入分类器的特征数据维度的影响。 由图7 与图8 可见,随着维数d的增加,分类精度也缓慢增加,最终趋于平缓。 且由图7 可以看出,相比其他对比算法,本文算法在各维数上的分类精度总体来说最佳,在低维数的情况下也能实现较高的准确率。

图7 在Dataset 3a 数据集上应用本文算法且p=2 时不同维度对分类精度的影响对比

图8 在受试K3b 上应用不同算法且p=2 时不同维度对分类精度的影响对比
上述这些结果表明,矩阵结构的数据中存在着重要的空间联系,不同特征提取方法对于空间信息和结构信息具有不同的提取能力,并且这种提取的效果决定了最终的准确率。 本文算法将协方差矩阵分成行和列两部分,能够对脑电数据中的空间和频率信息有更好的捕获能力,从而提取出更加具有判别力的特征。 利用核方法计算高维空间中的核矩阵以及类内和类间权值矩阵,并将低维脑电数据进行转换,获得新的投影矩阵进行特征的提取,相比于传统的流形学习特征提取方法增加了对非线性特征的提取能力,同时保留了对空间和频率信息的利用,在处理脑电数据上的表现有了一定程度的提升。
4 结论
本文提出了核-双向二维判别局部保留投影算法,将原始样本投影到了高维的核空间当中,使得线性不可分的脑电数据在高维空间中的特征更加具有区分性。 改进后的算法利用核方法计算高维空间中的核矩阵以及类内和类间权值矩阵,并将低维脑电数据进行转换,获得新的投影矩阵以进行特征的提取。 实验结果表明,核方法可以有效地在高维特征空间提高算法性能,相比于传统流形学习算法增加了对非线性特征的提取能力,同时保留了对空间和频率信息的利用,在处理脑电数据上的表现有了一定程度的提升。 本文算法在判别特征的提取上有了较好的优化和改进。

