基于深度学习的过程控制回路性能评估
赖新熠,蔚伟,钱玉良,宋红启
1.上海电力大学,上海,200090;2.华电电力科学研究院有限公司,浙江,杭州,310030
0 引言
在流程工业中存在大量的控制回路,其中60%的控制回路控制性能达不到要求[1],因此需要及时调整性能不佳的回路,其中的首要步骤就是对过程控制回路进行控制性能评估。Harris提出了基于最小方差的性能指标,为控制评估的研究奠定了基础[2]。广义最小方差在原最小方差的基础上将控制信号引入评估指标,拓展了最小方差方法的评估范围,增强了鲁棒性[3]。线性二次高斯基准同时考虑系统的输入输出,通过改变权重因子得到LQG最优控制权衡曲线,通过曲线可得到输入输出方差性能指标和控制性能下限[4]。目前大部分评估方法计算复杂度大,对回路特征的提取有局限性,对回路过程数据的处理有主观性。为解决这些问题,本文提出基于深度学习和一维卷积神经网络的过程控制回路性能评估方法。首先,使用带遗忘因子的线性回归算法和振荡检测指标进行综合评估,对控制回路的过程输出信号进行初步评估;然后利用一维卷积神经网络完成特征提取和性能评估;最后通过仿真实验验证方法的有效性。
1 综合控制回路评估指标
1.1 带遗传因子的线性回归算法
带遗忘因子的线性回归算法基于原始过程的输入输出数据,其核心方法是通过时间序列分析法建立过程扰动模型,构建多维矩阵计算最小方差指标,这种方法有着计算复杂度大大简化、评估正确率高、对数据变化适应性强的优点[5]。ILR的具体指标为:
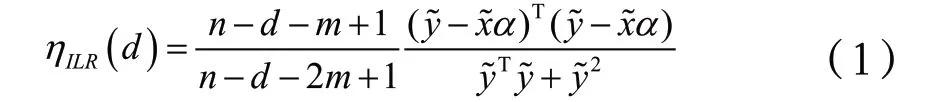
ILR指标的取值范围介于0与1之间,越靠近1控制性能越好,越靠近0性能越差。带遗忘因子的线性回归指标是一种定量分析方法,是对过程回路的整体评估,对局部范围内的特征提取较为不足,且数据处理和运算过程中易造成回路信息的损失,因此需要对ILR指标进行补充。
1.2 振荡指数
在典型过程环节运行时,有30%的回路由于振荡参数调节过紧、控制阀门粘滞、外部振荡干扰等原因产生回路振荡;而当原始信号发生振荡,其自相关函数也会发生振荡[6],因此通过自相关函数定义振荡指数为R=a/b。其中,a表示ACF曲线中首个波峰值到前两个波谷值连线的直线距离,b表示首个波谷值到首个波峰值和初始值连线的直线距离,示例如图1所示。R的取值范围从0到1,当振荡指数R>0.5时,输出数据或误差数据存在明显振荡。

图1 振荡指数示例图
由此,结合带遗忘因子的线性回归算法和振荡指标,构成对过程控制回路的综合评估,以ILR指标作为主要依据,将回路划分为优秀、良好、中等、较差、极差五个等级,设定的临界值分别是0.8、0.7、0.6、0.5、0.3;同时,以振荡指数作为补充,设定临界值为0.5,若受评估数据的振荡指标大于0.5,则该数据的评估等级被修正到低一级别。
2 一维卷积神经网络
卷积神经网络是在深度学习深层神经网络中得到广泛应用的结构,通过卷积层和池化层相互连接,压缩放大所提取的特征,通过全连接层汇总特征并送入输出层,最后用分类器将数据分类,有着局部连接、权值共享、池化操作及多层结构等优良特性,主要应用在图像分类、人脸识别和ECG分析等方面[7]。
传统卷积神经网络是针对二维数据的,如图片、视频等,一维卷积神经网络是对原有结构进行改进,将二维结构改造成一维,使其适用于一维数据,相较于传统卷积网络结构,一维卷积神经网络有着计算复杂度更低、网络结构更简易及占用计算资源更少的优点[8]。其结构如图2所示,各层的结构和输出都是一维。

图2 一维卷积神经网络结构图
3 实验验证
3.1 实验样本
仿真搭建火电厂锅炉汽包水位控制系统,以单冲量控制系统为例,回路在受到外界扰动的情况下,通过跟踪输入值控制汽包水位维持在设定水位。实验样本由仿真控制回路的过程输出数据构成,分为受到扰动时不变和受到扰动时改变两组,每条样本的采集数据点10000个,每500个采集点为一组,则一条样本数据被分为20组。通过评估方法评估每组数据,收集各等级(优秀、良好、中等、较差、极差)数据各500条,由此构成的两组数据集分别为时不变扰动数据集1#和时变扰动数据集2#,数据集总结如表1所示。

表1 数据集容量表
3.2 实验步骤
通过仿真搭建火电厂锅炉汽包水位控制系统来获得回路过程输出数据,对过程数据使用时序分析方法拟合建模,综合计算带遗传因子的线性回归指标和振荡指数,再根据评估等级的划分规则得到确切的回路性能评估等级,接着使用一维卷积神经网络对输入数据进行学习,提取数据中的特征并进行性能评估,主要步骤如下。
(1)获取并处理过程输出数据。锅炉汽包控制系统单冲量控制仿真模型为单闭环比值控制回路,回路通过跟踪设定水位以及调节汽包水位,使其维持固定水位不变。
实验通过改变控制器参数来输出在不同控制性能下的过程输出数yi=x(n)(n=1,2,3,…10000),x(n)表示第n个采样点的输出值,i为数据标号。设定采样周期为1秒,每一条样本数据共采样10000个采样点,又以500采样点为周期将一条样本数据划分为n小段数据片段yik=x(n)(n=1,2,3…20),yik表示第i条数据样本的第k段数据。获取数据后对每条样本数据进行时序随机性分析处理,建立关于过程扰动的时间序列ARIMA模型[9]。
(2)使用综合评估算法评估等级,划分数据集。以每组数据片段为单位,经过计算得到回路性能ILR指标ηILR;同时通过时序模型做出自相关函数曲线,按照振荡指数公式及相关定义得到振荡指数R,获得这两个指标之后,再根据综合评估回路控制性能规则得到回路控制性能等级Lik。
之后将数据样本片段yik与回路控制性能等级Lik一一对应并划分数据集,按扰动结果不同划分成两个不同的数据集,分别为时不变数据集YUC={yik,Lik}和时变数据集YC={yik,Lik}。
(3)使用一维卷积神经网络评估控制回路。以时变数据集为例,首先对数据集数据yik进行预处理,将数据进行标准化处理,缩放到[-1,1]范围内,再将数据集YC按7:3的比例乱序分成训练集YC_train和测试集YC_test。
参考一维卷积神经网络结构图搭建深层网络,包含多个卷积池化层,同时按照高斯分布初始化权重和偏置。随后,将训练集数据YC_train输入网络,通过卷积过程提取特征和池化过程降采样。经过多层网络的不断卷积池化过程后,全连接层将特征数据中首尾相连的数据送入输出层,输出层通过分类器对数据分类得到整个网络的输出;接着,通过损失函数反向传播优化网络的参数设置,参数优化后就得到了训练完成的一维卷积神经网络。最后,使用测试集YC_test测试模型对控制回路评估的准确性,并对模型评估性能进行评价。
(4)实验分析。设置对照实验组,分析实验结果并得出结论。
3.3 实验结果分析
权衡评估的准确性以及模型训练的时间,经过大量实验优化后得出以下结果。最终模型中卷积层共4层,每层都由2层的卷积层构成来充分提取特征,对应池化层为4层;全连接层由一层全局平均池化层和一层参数较少的全连接层构成,该结构能够减小模型参数,也能防止过拟合现象;输出层使用softmax多分类输出5个等级;此外在全连接层和输出层之间再加入一层dropout层来防止过拟合。
将时不变数据集1#和时变数据集2#输入模型,经训练后得到的结果如表2所示,其中acc与loss指标分别表示模型训练的准确率和损失函数值,两项指标分别越接近1和0,表示模型的训练效果越好;AUC指数为分类正确率大于分类错误率的量化指标,使用AUC指数来衡量模型的评估效果,数值越大说明模型效果越好,准确率越高[10]。由结果可知,一维卷积神经网络模型对于时不变数据的评估效果略微高于时变数据,但是模型对于时变数据的训练时间较短,达到最优模型的迭代次数也较少;同时,一维卷积神经网络模型对于两种数据集都得到了较高AUC值,说明该模型有着良好的评估效果,是一种控制回路评估的可行且有效的方法。

表2 模型训练结果
4 结语
针对控制回路性能不佳的问题,本文提出使用深度学习方法进行控制回路评估。首先使用综合评估指标对数据进行初步评估,接着构造一维卷积神经网络模型提取数据特征,直接得出控制回路的性能评估等级。仿真实验表明:综合评估算法能正确评估出回路的真实控制性能,一维卷积神经网络模型在达到较高准确率的情况下,平均用时较其他模型更短,且能够实现对控制回路进行实时性能评估。

