基于BIM的地图构建与导航研究
陈宇帆,段中兴,2
(1.西安建筑科技大学 信息与控制工程学院,西安 710055;2.西部绿色建筑国家重点实验室,西安 710055)
0 引言
随着城市化发展的进程,出现了越来越多的高楼大厦与大型公共建筑,实现智能与自动化成为当今社会进一步发展的新契机。随着各类机器人的出现,使得人们的生产生活方式发生了变革,解放了很多人力劳动,同时也存在着一些棘手的问题。
由于建筑室内环境的复杂与多变,移动机器人需要在技术性能上要求更高。当前地图构建方式大多采用SLAM (simultaneous localization and mapping) 技术[1],让机器人通过传感器在未知的环境中得到识别信息,并逐步获取相关地图。当环境发生较大变化时,SLAM构建的地图将无法使用。并且面对面积较大的场景时,使用SLAM技术也会使得构建地图的过程变得更加复杂和繁琐。由于建筑信息模型BIM (building information modeling)技术的快速推进,因此在工程建设中越来越广泛使用BIM模型,获取建筑的信息也更加的准确及时[2]。使用BIM模型能够快速创建室内地图,因此将BIM模型与移动机器人室内导航相结合,能够提高机器人工作的效率。对于路径规划,目前比较常用的有人工势场法[3]、A*算法[4]、迪杰斯特拉算法(Dijlstra)[5]、遗传算法[6]、蚁群算法[7]等。动态窗口法(DWA)是目前局部路径避障的主要算法,应用于实时碰撞避免策略[8]。文献[9]对A*算法进行了改进,使得规划的路径更加平滑,但是对于有随机障碍物出现的情况不适用;文献[10]将Dijkstra算法与DWA算法相融合,在全局路径中规划出最短路径,并在局部路径规划中实现避障效果,但是没有考虑动态障碍物与机器人之间的距离,容易使得机器人在狭窄空间内无法通过;文献[11]中将传统A*算法的8邻域搜索改为5邻域搜索,使用DWA算法进行局部避障,使得路径距离变短且平滑度提高,但是没有考虑到其5个邻域方向同时存在障碍的情况,容易使得全局路径无法规划。
针对上述问题,本文在地图建立过程中采用BIM模型,提取建筑物的空间信息,从而使地图构建效率得到提高,让移动机器人能够快速获取和熟知室内环境。在室内路径规划中,采用全局路径与局部路径相结合,对A*算法进行改进,扩大其搜索邻域,考虑机器人通过的安全性,当有动态障碍时,采用DWA算法进行避障,保障运动的连续性。
1 BIM信息提取与地图构建
建筑信息模型BIM(building information modeling)是一个生产建筑数据和使用建筑数据的过程[12],基于模型的智能化流程,包含与物理特性和功能特性相关的数据,BIM技术能更好的还原从概念到施工的建筑模型,使得建筑建造和运营建筑基础设施变得更加高效、更加精细化和透明化。
使用Autodesk Revit软件进行BIM建模,可以对现实三维事物进行准确的模拟,并且能够呈现出准确的信息。
1.1 IFC简述
IFC(industry foundation class)是针对BIM数据交换的唯一的开放式标准格式。文件IFC是一种交换格式,用于不同软件系统之间交换建筑设计和建造中使用的建筑数据模型,从而达到数据共享。IFC标准分为4个结构层次,分别为资源层、核心层、交互层和领域层[13],4个层次共同来完成信息资源的稳定。IFC 中运用 EXPRESS 语言描述建筑产品数据[14]。EXPRESS 是一种标准化数据建模语言,其定义在 STEP 国际标准中[15]。EXPRESS语言与其他编程语言不同,更看重对计算机大规模数据的可读性,从而实现对数据信息的描述。
1.2 IFC数据前期处理
通过BIM建模,导出IFC文件,并对IFC文件进行解析,提取出所需要的室内几何信息[16-17]。IFC文件的基础结构包括项目的基本内容、基本空间结构以及几何表示。项目的基本内容主要由IfcProject提供,项目的基本空间结构主要由IfcBuilding提供,几何表示主要由IfcBuildingElement提供。在IFC文件中,实体的属性具有继承关系,属性分为:直接属性、导出属性和反属性。其中直接属性很直观的表达了构件信息,导出属性是通过不同构件实体的属性来构成表达,而反属性是构件可以通过关联实体从而获得相关信息。IFC文件的数据部分包含了构建模型的坐标位置、属性值、长宽高、空间隶属关系等相关信息。IFC数据段中的部分坐标信息如下:
#138=IFCCARTESIANPOINT((0.,0.,10800.));
#140=IFCAXIS2PLACEMENT3D(#138,$,$);
#141=IFCLOCALPLACEMENT(#32,#140)
其中#141是对象位置信息(ObjectPlacement),IFCLOCALPLACEMENT(#32,#140)描述了该构件的相对位置几何坐标,这里几何坐标引用了#32父坐标体系。
#140=IFCAXIS2PLACEMENT3D(#138,,);指定了局部坐标系的原点位置,符号代替语句中次要信息。#138= IFCCARTESIANPOINT是位置信息,表示((0.,0.,10800.)位置处。
使用IFC解析工具对IFC文件进行解析,对所需的室内模型构件的几何信息进行提取。如图1为其中一个柱IfcColumn的属性和地点信息。

图1 IfcColumn的属性和地点信息
从属性中可以看出构件的实体名、类型、标签以及轮廓等。从地点中可以看到构件的位置坐标、长宽高以及所处的楼层信息等。图中这个柱子长度为600 mm,宽度为600 mm,高度为3 400 mm。位置坐标为(9 082.337 744,-1 837.497 743,10 800)。
1.3 构建地图
获取建筑环境的边界顶点坐标,栅格平面的长为L=Xmax-Xmin,宽为W=Ymax-Ymin。则栅格平面行数为i=[L/S],列数为j=[W/S],S为每个栅格所代表的实际长宽。将几何信息映射到栅格平面时,使用构件在二维平面图的起终点坐标进行映射,对应网格属性为1。(属性为1代表不可通行,为0代表可通行)。当构件映射不满一个栅格时,则补齐这个栅格作为不可行区域。地图构建过程如图2所示。

图2 地图构建过程
2 A*算法的改进
2.1 传统A*算法
A*(A-Star)算法是一种启发式搜索,利用启发函数对搜索过程进行指导,在静态环境下的路径规划, A*算法不但能获得较短路径,并且其搜索效率比较高,广泛应用于室内机器人路径搜索、游戏动画路径搜索。A*算法的估价函数可以表示为:
f(n)=g(n)+h(n)
(1)
f(n)是从初始状态经由状态n到目标状态的代价估计,g(n)是状态空间中从初始到状态n的实际代价,h(n)是从状态n到目标状态的最佳路径的估计代价。
2.2 48邻域扩展
传统A*算法为8邻域搜索,也就是在该点周围的8个相邻栅格方向搜索,使得机器人的转向方向也被限制于π/4的整数倍,这样规划出来的路径转折角度较大。如果转折角度过大,不利于机器人在室内狭窄空间移动,也会使得移动时间变长,降低了工作效率。因此,将原先的搜索范围扩展至48邻域搜索如图3所示,对8个方向上每2个方向(如D、E之间)之间再增加3个方向搜索,由原来的8个方向变为32个方向,这样会使机器人在方向上有更多选择,减少转向次数,更加流畅的进行作业。图4为使用48邻域搜索的路径规划结果图。S为起点位置,D为终点位置,直线所连接的方块为规划的路径,周围区域为48邻域搜索空间。

图3 A*算法的邻域搜索空间

图4 48邻域搜索结果图
2.3 搜索路径改进
传统A*算法在规划路径时没有考虑到机器人本身的轮廓大小,规划出来的路径容易紧贴墙壁或者障碍物。由于室内环境会有很多门或者相邻柱体,且随机障碍物较多,若按照传统A*算法规划出来的路径移动,会使得机器人与障碍物相撞,更有可能损伤机器人机身。因此,除了对传统A*算法在搜索方向上进行扩展,还需要考虑机器人安全性,将规划出来的路径进行改进。
机器人在移动过程中,将规划出来的路径与障碍物的距离记为s(m),机器人机身半径记d(m),规定安全距离为0.2 m,当s≥d+0.2,则表示规划的该路径可通过,反之,不可通过。
3 进A*与动态窗口法的融合算法
3.1 动态窗口法
动态窗口法DWA(dynamic window approach) 作为局部路径规划避障的主要算法[18],能够接受全局路径规划生成的路径以及里程计的信息、地图的信息,输出为底盘运动的速度信息。算法流程为:根据机器人当前的速度,计算出当前可采样的速度范围,然后对采样的每一组速度都依据运动模型,模拟一段时间内的路径。把所有采样速度生成的路径都模拟出来后,接着根据评价函数对每一条路径都打分,然后选取得分最高的一条路径,那么这条路径就对应了一组采样速度,就把这一组速度作为机器人下一时刻的速度,那机器人就会以新的速度继续移动,这时候算法就会进入新的循环,以新的速度计算新的采样速度范围,然后模拟路径,再次根据得分选取路径和速度,把选取到的速度用于下一个时刻,以这种流程不断循环下去。所以这些模拟路径是不断的在变化,因为在不断的进行采样、模拟、评价再采样,一直刷新模拟的路径,那机器人就会不断的调整自身的速度和方向,往目标点移动,从而实现导航的功能。
3.1.1 机器人运动学模型
设机器人在全向运动过程中,在X方向的速度为Vx,在Y方向的速度为Vy,角速度为w。若将机器人在相邻时刻两点之间的轨迹看成直线,那么在△t的时间里,运动模型可表示为:
由X方向速度产生的机器人的坐标变化为:
△xx=vx△tcosθt
(2)
△yx=vx△tsinθt
(3)
由Y方向速度产生的机器人的坐标变化为:
△xy=-vy△tsinθt
(4)
△yx=vy△tcosθt
(5)
机器人下个状态的位置:
x=x+vx△tcosθt-vy△tsinθt
(6)
y=y+vx△tsinθt+vy△tcosθt
(7)
θt=θt+w△t
(8)
3.1.2 速度采样
依据机器人的运动模型,通过采样多组速度,模拟出一段时间内的路径。
1)机器人最大速度与最小速度限制。
vm={(v,w)|v∈[vmin,vmax]∧w∈[wmin,wmax]}
(9)
式中,Vm为机器人速度;v为线速度;w为角速度。
2)机器人加速度限制。电机的力矩是有限的,电机性能也会有所影响,使得机器人移动时的加速度不能在短时间内无限大。所以加速度是限制了采样速度范围的一个因素。因此,加速度限制范围为:
Vd={(v,w)|v∈[vc-vb△t,vc+va△t]∧w∈
[wc-wb△t,wc+wa△t]}
(10)
式中,Vd为机器人受加速度限制后的速度;Vc为当前线速度;Va为最大线加速度;Vb为最大线减速度;Wc为当前角速度;Wa为最大角加速度;Wb为最大角减速度。
3)预留安全距离。当有障碍物时,机器人不是立马能够停下来,因此需要预留安全距离范围为:
Va={(v,w)|v≤(2dist(v,w)vb)1/2,w≤
(2dist(v,w)wb)1/2}
(11)
式中,dist(v,w)为机器人与障碍物之间的距离。
3.1.3 评价函数
在利用采样速度模拟了很多路径以后,对速度的选择需要使用评价函数来评估轨迹的好坏[19-20]。评价函数用以下表示:
G(v,w)=σ(α·heading(v,w)+β·dist(v,w)+
γ·velocity(v,w))
(12)
式中,heading(v,w)为方位角评价函数,指的是机器人与目标之间的角度差,角度差越小,得分越高;dist(v,w)为机器人与最近障碍物之间的距离,距离越远,得分越高;velocity(v,w)为轨迹对应的速度大小,速度越大,得分越高。
为了避免这三项不同类别的得分基数相差太大,影响结果。比如方位角的角度差得分在0~180之间,而障碍物距离得分可能都在5以内,这样就容易掩盖了障碍物距离的影响。因此,需要对这3个方面的得分进行归一化处理,把每一项的得分占比算出来再相加。归一化如下:
(13)
(14)
(15)
在归一化处理后,对每一部分赋权重,不同的权重值会影响机器人选取的路径。将这3方面综合起来的物理意义就是使得机器人避开障碍物,朝着目标点以较快的速度移动。
3.2 融合算法
将全局路径规划与局部路径规划相结合,先由全局路径规划器规划出一条大致的路径,接着局部路径规划器又会将它划分为许多小区段,再完成整个局部路径规划。相当于是把一个总目标分成很多个小目标然后依次达成。这样做的好处是在全局路径规划的时候,对地图保存过的障碍物进行避障,而在局部路径规划的时候,会对新增的障碍物信息也进行避障。并且它支持对动态的障碍物进行避障。本文算法的流程如图5所示。

图5 算法流程图
4 实验与仿真
在获取到的楼层地图上进行短距离和长距离两组路径规划,每一组实验中都采用传统A*算法、改进A*算法、改进A*与DWA的融合算法(无障碍物)、改进A*与DWA的融合算法(有障碍物)来进行路径规划。第一组实验的起点坐标为(10,28),终点坐标为(27,14),动态障碍物设置为2个,坐标为(14,27)、(23,20),结果如图6和图7所示;第二组实验的起点坐标为(15,16),终点坐标为(89,27),动态障碍物设置为3个,坐标为(32,22)、(83,22)、(84,22),结果如图8和图9所示。同时,记录了每组实验中各算法路径规划的运行时间和路径长度,对传统A*算法与改进A*算法的累计转折角度进行了计算,结果如表1~4所示。

图6 第一组路径传统与改进算法轨迹图
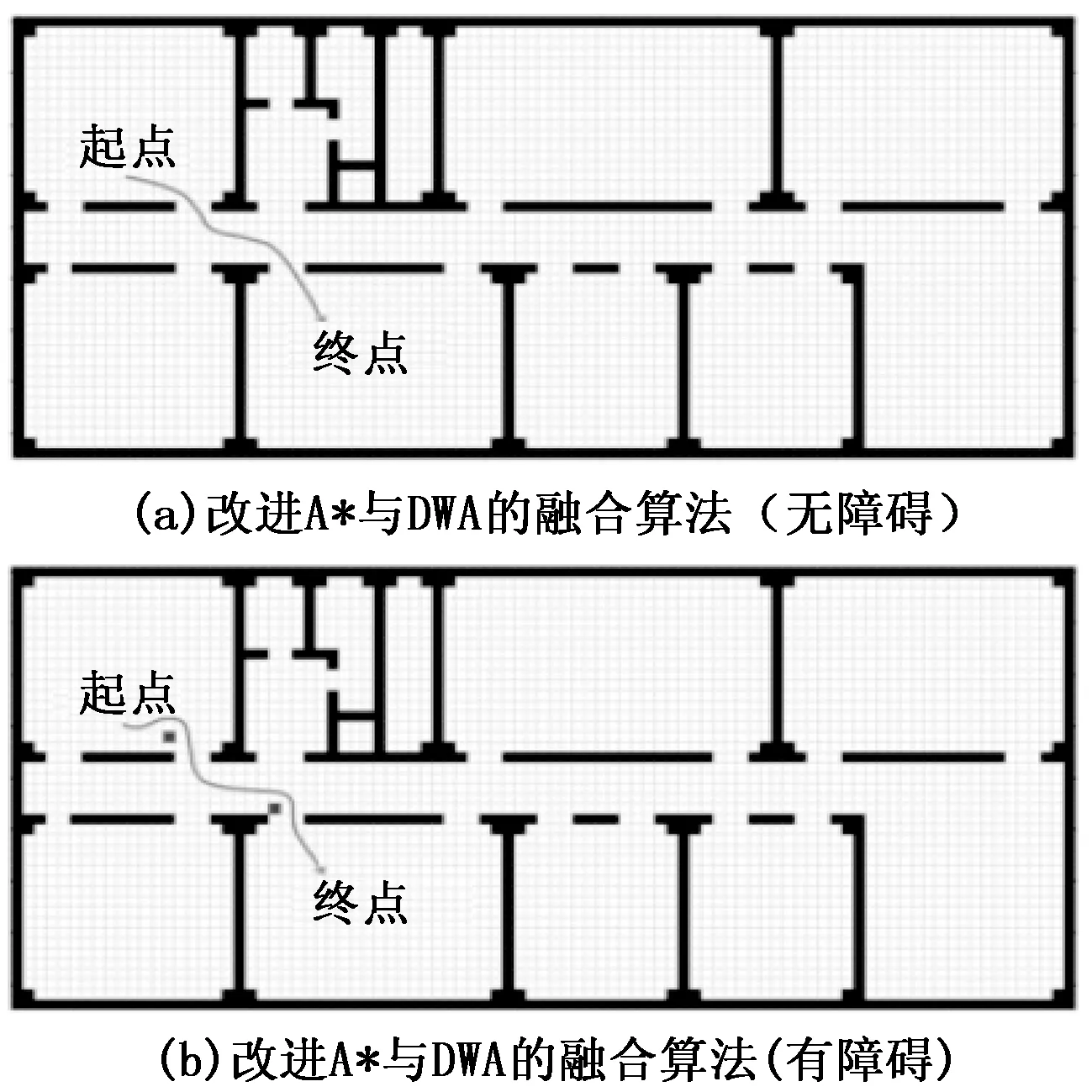
图7 第一组路径融合算法轨迹图

图9 第二组路径融合算法轨迹图

表1 第一组路径传统与改进算法的性能比较
由图6和图8可以看出:传统的A*算法在规划路径时,路径与墙或门的距离较近,安全性比较低。而使用改进的A*算法考虑了机器人安全性的问题,增加了路径与障碍物的安全距离,使得机器人不再靠着墙壁移动,确保了机器人能够顺利通过。由表1表2 可知,改进的A*算法比传统A*算法在运行时间上快了2倍以上,由于节点转折角度差的减小,改进后的两组路径长度也都相对的优化。其次,第一组仿真实验传统算法累计转折角度为225°,改进算法为162°,第二组仿真实验原始算法累计转折角度为225°,改进算法为128°,改进的A*算法优化了搜索角度,比传统A*算法的累计转折角度减少了28%以上。综合来看,改进后的算法在路径规划在性能上都有进一步的改善,且搜索效率有所提升。

表2 第二组路径传统与改进算法的性能比较
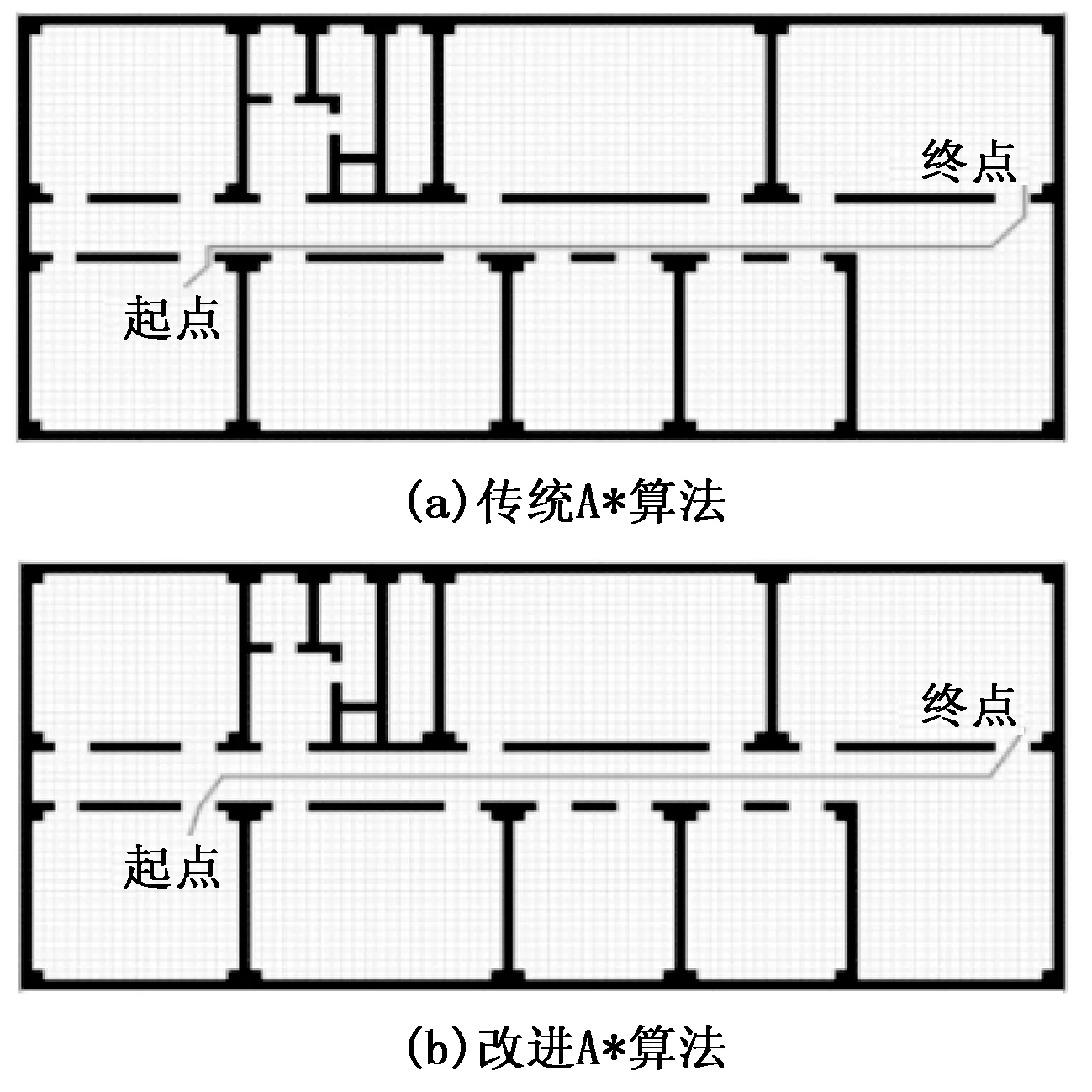
图8 第一组路径传统与改进算法轨迹图
采用改进A*与DWA的融合算法规划的路径如图7、9所示,分别为无障碍物和有障碍物两种情况。动态窗口法的参数设置如下:机器人运动学模型间隔时间为0.1 s,最大速度为1 m/s,最大角加速度为20°/s,速度分辨率为0.01 m/s,角加速度分辨率为1°/s,加速度为0.2 m/s2,角加速度为50°/s2。评价函数参数为:α=0.2,β=0.2,γ=0.1,预测时间周期为3.0 s。改进A*与DWA的融合算法的配合过程就是改进的A*算法出一条大致的路径,然后DWA算法会把改进的A*算法规划的路径分割成很多段,大目标分割成很多小目标,然后用DWA算法依次导航到每一个小目标点。当没有障碍物时,融合算法比改进的A*算法的路径更加连续,平滑度更高;当有动态障碍物出现后,融合算法能够及时实现避障,由表3所知,无障碍物时,使用融合算法第一组路径规划整个算法用时30.99 s,路径长度为13.053 6 m;当出现两个障碍物时,整个算法用时31.89 s,路径长度变为14.402 6 m。由表4所知,无障碍物时,使用融合算法第二组路径规划整个算法用时87.35 s,路径度为48.241 8 m;当出现3个障碍物时,整个算法用时89.13 s,路径长度变为49.872 5 m。因此随着障碍物的出现,运行时间和路径长度也理应有所增加。综合来说,融合算法规划的路径平滑度更好,并且能及时避开出现的随机障碍物,使得机器人在室内场所的移动更加安全。

表3 第一组路径融合算法的性能比较

表4 第二组路径融合算法的性能比较
图10为选取了第一组短路径下传统A*算法和融合算法的控制参数对比,机器人在传统A*算法下的线速度和角速度变化范围较大,变化不连续,这样会不利于机器人的移动,长时间会损伤机器人机身。而在融合算法下的线速度变化波动较小,比较平稳,并且角速度的曲率变化比较平滑连续,更符合机器人的动力学控制,也会使得机器人整个行驶过程变得流畅。
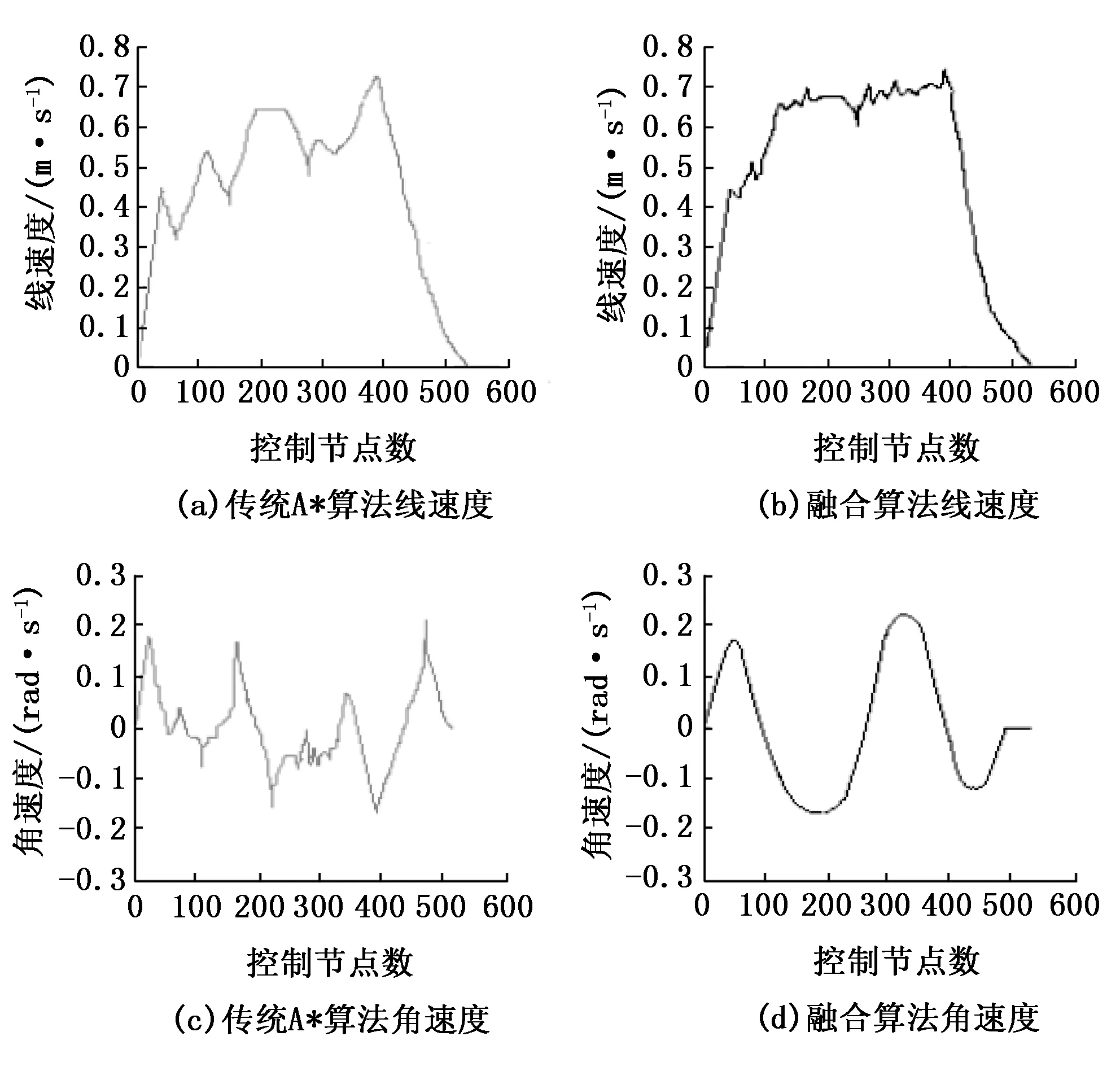
图10 第一组路径控制参数对比
5 结束语
通过BIM技术提取建筑空间信息,节省了机器人获取室内环境的时间,同时也提高了地图构建的效率。针对移动机器人路径规划问题,对传统A*算法进行了改进,通过仿真结果得知累计转折角度减少了28%以上,运行时间也快了2倍。同时,设置了路径与障碍物的安全距离,保证了机器人的安全性。此外,为了解决移动机器人行驶过程中遇到动态障碍物的问题,将改进A*的算法和动态窗口法相结合,并对融合算法也进行了实验仿真和性能对比,验证了本文的融合算法路径连续性更高,达到了避障能力,更具有环境适用性。

