基于AE-AMPSO-SVM 的地下电缆早期故障定位方法

王文凯，刘明，邓斌

（云南民族大学电气信息工程学院，云南昆明 650504）

地下配电网多采用电缆作为配电线路。然而，电缆在外部环境的影响下容易老化[1]，从而引发以间歇性电弧为特征的电缆早期故障[2]。

目前，电缆早期故障定位的主要研究成果有：通过误差计算和参数估计的方法估计初始故障位置[3-4]。此类方法计算量少，精度高，但推广性差；利用特征提取方法提取故障点故障信号特征，使用人工智能方法对故障点进行定位[5-7]。此类方法推广性强，但人工智能方法依赖特征提取方法，由于小波变换等特征提取方法客观性差，易引入人为误差。

故文中提出了基于自动编码器(Auto-Encoder,AE)与自适应变异粒子群优化算法(Adaptive Mutation Particle Swarm Optimization algorithm,AMPSO)优化支持向量机(Support Vector Machine,SVM)的地下电缆早期故障定位方法。

1 自动编码器

自动编码器（Auto-Encoder）是一种输入层与输出层神经元数目相同的自动编码神经网络。它通过限制隐藏层神经元的数目，学习原始数据的低维表示，提取训练数据中的最显著特征[8]。其结构示意图如图1 所示。

图1 自动编码器结构示意图

图1中，xi为输入层神经元数据，hi为隐藏层神经元数据，xdi为输出层神经元数据，b1为输入层偏置，b2为隐藏层偏置。

自动编码器的训练过程可由式（1）～（5）表示：

其中，x为原始数据，xd为自动编码器重构的数据；σe为Sigmoid 激活函数，σ为Tanh 激活函数；b1和b2是输入层和隐藏层的偏置，W1和W2分别为输入层和隐藏层以及隐藏层和输出层的连接权值，W分为W1和W2，b分为b1和b2，M是样本总数。

隐藏层神经元数目为特征提取数量的目标值，为权衡特征维数与训练误差，选取合适的隐藏层数目是十分必要的。在训练自动编码器时，利用对比训练误差大小来确定隐藏层神经元的个数[9]。文中以重构数据与原始数据的均方误差作为标准，选取合适的隐藏层神经元数目，从而优化自动编码器性能。

2 改进支持向量机

支持向量机的整体性能很大程度上取决于超参数的设置。使用自适应变异粒子群算法改进支持向量机，建立PSO-SVM 电缆早期故障定位模型。

2.1 支持向量机

SVM 在解决回归问题时，对于给定的训练样本D={(x1,y1),(x2,y2),…,(xn,yn)},xi∈ℝ 为原始数据，yi∈ℝ为数据原始对应值，学习得到一个形如式（6）的回归模型。

其中，f(x)为模型输出值，ω和b为待定参数。

支持向量机回归模型(Support Vector Regression,SVR)的损失计算则是以预测模型f(x)为中心构建了一个宽度为2ε的间隔带。只有落在隔离带外的训练样本，才会计算损失；落在隔离带内，则被认为预测是正确的[10]。因此，SVR 问题可以形式化为：

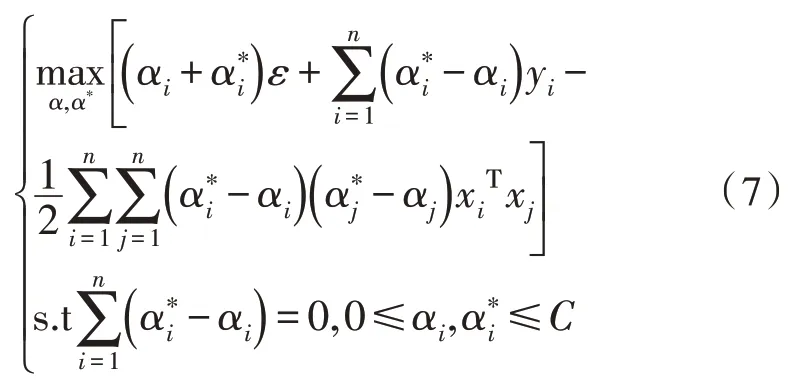
其中，αi、是拉格朗日乘子，ε是间隔带宽度。上述过程满足KKT 条件，并考虑特征映射的形式，则SVR 的解为：

其中，κ(xi,xj)是核函数，b为偏移项。高斯核函数能够实现非线性映射且拥有较大的收敛域,因此文中使用高斯核函数。

2.2 支持向量机模型的优化及训练

自适应变异粒子群优化算法(AMPSO)凭借其自适应变异操作扩大粒子搜索空间，从而使粒子可以跳出先前搜索的最佳位置并在更大的空间中搜索，同时可以保持种群的多样性并提高算法寻优的可能性，避免了算法陷入局部最优解[11]。因此，选择自适应变异粒子群优化算法对SVR 模型进行参数寻优，优化过程如下：

步骤一：选择均方误差函数为适应度函数，如式（9）所示:

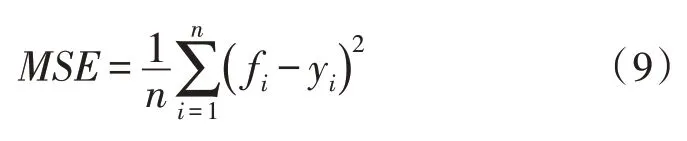
其中，n为样本总数，fi为样本第i个模型输出值，yi为样本第i个真实值。

步骤二：设置自适应变异粒子群优化算法各个参数的初始值。

步骤三：根据当前种群的参数值生成局部最优值pbest和全局最优值gbest。

步骤四：按照式（10）更新惯性权重[12]；

步骤五：根据式（11）和式（12）更新粒子的速度和位置，并根据式（13）对粒子位置进行变异操作。

其中，k为当前迭代次数，ωv为弹性惯性权重，c1和c2为加速因子，r1和r2是[0,1]范围内的随机常数。xid为粒子的位置,vid为粒子的速度。

其中，p为变异阈值，rand1 和rand2 均为(0,1)之间均匀分布的随机值，ceil 函数为四舍五入函数，popcmax为参数c变化的最大值，popcmin为参数c变化的最小值，popgmin为参数g变化的最小值。

步骤六：根据式（9）计算适应度，更新pbest和gbest。

步骤七：当进化次数达到给定值，停止搜索，将搜索得到的最优参数c和g赋予SVR 模型。

3 电缆早期故障定位方法构建

文中提出基于AE-AMPSO-SVM 的地下电缆早期故障定位方法，算法流程图如图2 所示。

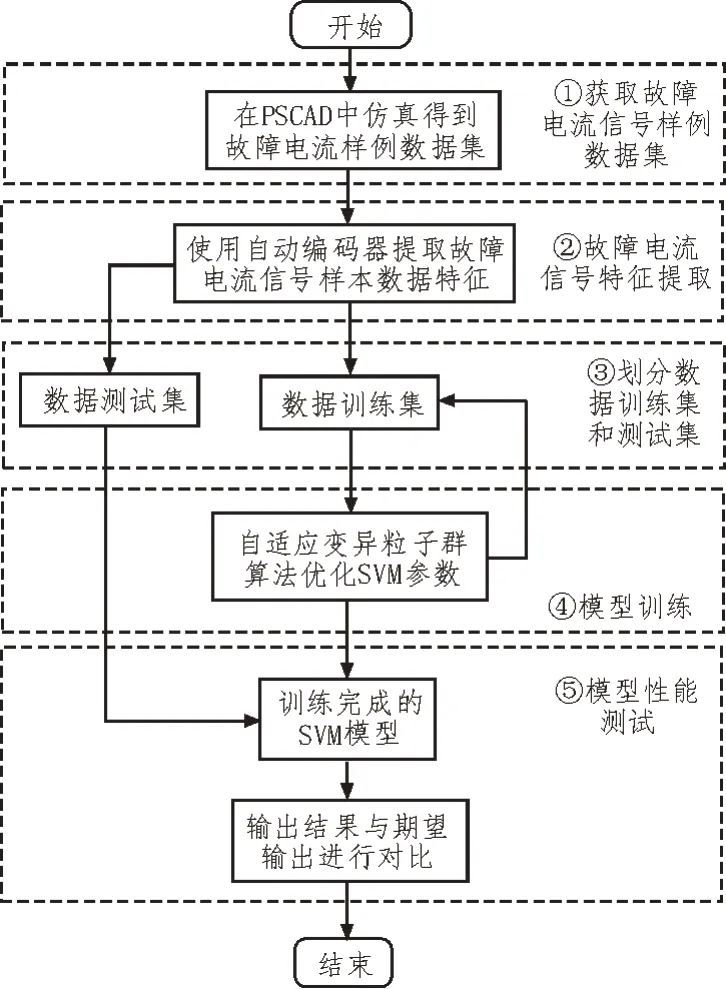
图2 算法流程图

①获取故障电流信号样例数据集。在PSCAD中搭建仿真模型，获得故障电流信号数据集。

②故障电流信号特征提取。使用训练好的自动编码器，对故障电流信号样本集数据进行特征提取与数据维度压缩。

③划分数据训练集和测试集。标记数据集为故障点的发生位置，样本为每个故障点在变电站端测得的三相电流数据。

④模型训练。在训练集样例空间中，训练改进的支持向量机。

⑤模型性能测试。使用训练好的支持向量机对测试样本数据集进行预测，评估其性能。

测试训练完成的支持向量机模型可以根据输入的单端电流数据进行电缆早期故障的定位。

4 仿真

4.1 数据获取

该文使用PSCAD/EMTDC 电力系统暂态仿真软件建立了地下电缆早期故障仿真模型，结构如图3所示。

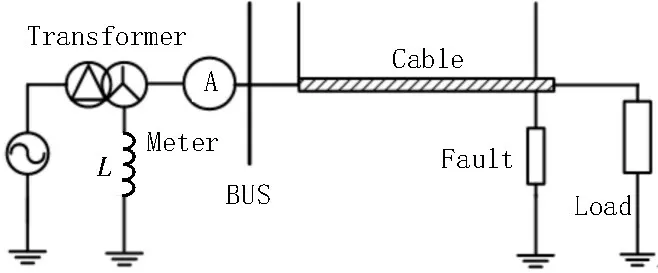
图3 地下电缆早期故障仿真模型

进行电缆早期故障模型仿真时，采样对象为变电站端的三相电流信号，信号的采样频率选择10 kHz[2]，仿真时长为0.1 s，每个样本有1 000 个采样点。馈线采用P 等值电路模型，变压器变比为35 kV/10 kV，馈线长度为20 km，从馈线首端1 km 处开始设置，每隔1 km 的位置做一次仿真[5]。故障持续时间按半周波故障和多周波故障分别设置为0.005 s和0.02s、0.04 s。

在故障仿真中，使用文献[13]中所述的改进“控制论”电弧模型对电缆早期故障进行模拟。电弧的仿真参数采用经验值[8]。即：Vso(弧隙每厘米压降)为75 V；Is(小电流接地系统金属性接地故障稳态电流的幅值)为7.818 A；β(常量系数)为7.56×10-6；电弧长度l为[5,10]，步长为1；短路电阻为0.1 Ω、10 Ω、100 Ω。

电缆早期故障多发生在电压峰值附近，因此选择在电压正半周和负半周的峰值附近进行仿真[4]，仿真故障相角如表1 所示。

表1 故障相角

因此每个故障发生位置处的样本数为540，样本总数为10 800。故障相的仿真电流波形如图4 所示。

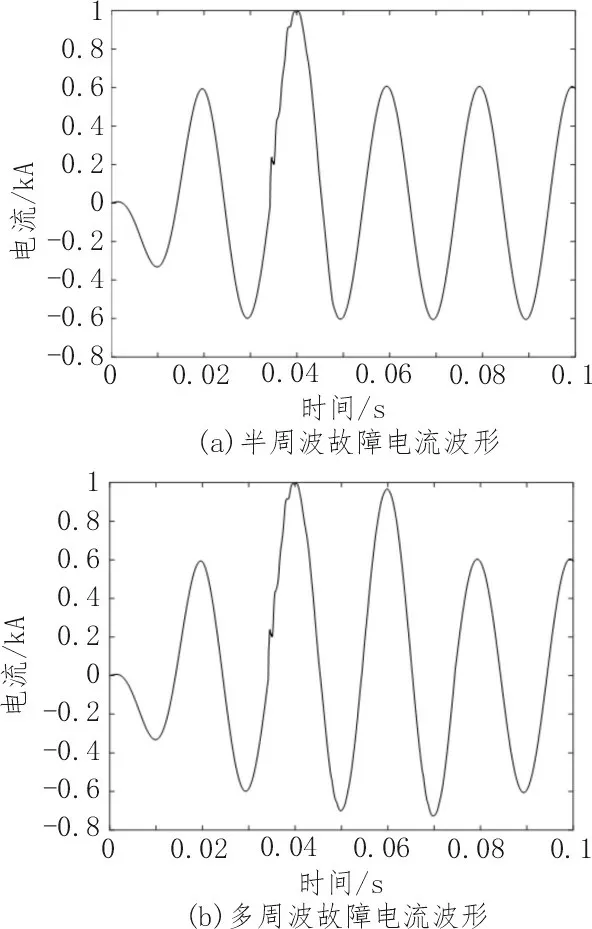
图4 电缆早期故障相电流波形

4.2 数据预处理

数据归一化是指将样本数据映射为[0,1]之间的小数。将所有数据集归一化为[0,1]，更容易进行梯度下降，这更有利于更新模型的参数[14]。因此，对采集的信号样本采取数据归一化处理，如式（14）所示：

xscale为经最值归一化处理后的数据，xk为采集到的样本数据，xmin为数据序列中的最小值，xmax为数据序列中的最大值。

4.3 自动编码器训练

自动编码神经网络隐藏层神经元个数设置为[50,1 000]，步长为50，训练次数为50 epoch，batchsize为128[9]。记录在不同隐藏层数目下训练时原始值和重建值之间的均方误差。不同隐藏层规模的均方误差如图5 所示。

图5 不同隐藏层规模的均方误差

根据均方误差，当自动编码神经网络隐藏层神经元数目自250 开始，均方误差随隐藏层神经元数目增多的改善不再明显。因此，为平衡自动编码器性能与数据降维效果，选择自动编码神经网络隐藏层的神经元数目为250个，即压缩后的数据维度为250 维。

4.4 支持向量机的训练

使用LIBSVM 工具箱在Matlab2019a 环境下搭建了支持向量机回归模型。自适应变异粒子群优化算法的参数设定如下：种群数量为20；最大迭代数为100；粒子向量维数为2。加速因子c1和c2分别为1.5、1.7，变异阈值p为0.5，弹性惯性权重ωv的最大值为0.9，最小值为0.4，中间取值按式（9）计算，参数c和g的取值分别为[1×10-3,100]和[1×10-3,1 000]，粒子位置取值为[-10,10]；粒子速度取值为[-10,10]。

使用自适应粒子群优化算法对SVM 参数优化的过程如图6 所示。

图6 AMPSO参数寻优的适应度曲线

经自适应变异AMPSO 寻优得到惩罚参数的值为40.171，核函数参数为0.001时，误差最小，选择此时的参数为最佳惩罚参数和最佳核函数参数。

4.5 模型评估指标

评估文中所提出的地下电缆早期故障定位方法的性能，采用故障定位误差百分比作为模型性能的评价标准[15]，如式（15）所示：

其中，Lpre表示计算距离，Ltar表示真实距离，Llen表示线路总距离。

文中将所提出的方法与其他方法进行了对比，对比结果如表2 所示。

表2 不同定位方法的比较结果

表2 中数据表明，文中所提出的基于改进支持向量机的地下电缆早期故障定位方法定位误差小于其他3 种方法的定位误差。自动编码器在对故障信号进行特征提取时提取到的数据特征较小波变换方法更为客观，更具代表性[16]。经自适应变异粒子群优化算法改进的支持向量机提高了定位的准确率。

5 结论

仿真结果表明，基于AE-AMPSO-SVM 模型的电缆早期故障定位方法能准确定位电缆早期故障，测量误差率为2.506 2%，定位准确率高于小波模极大值等现有方法。自动编码器特征提取效果优于小波变换等传统提取方法。经自适应变异粒子群优化算法改进后的支持向量机故障定位精度得到了提升。