基于经验模态分解的有载分接开关振动信号识别

吴 达，王 康，叶紫燃

（1.国网福建省电力有限公司电力科学研究院，福建福州 350007；2.四川华音盛安科技有限公司，四川成都 610095）

深入研究变压器有载分接开关的带电检测技术，正确及时地对有载分接开关的运行状态进行监测和识别以及缺陷诊断，能够提升电力系统供电安全性与稳定性，提升电力系统的安全性。有载分接开关故障诊断最常见的方法是振动信号分析法，由于其可在不停电情况下对分接开关的工作状态进行检测，在实际中得到了广泛的应用[1]。近年来，随着基于信号模态分解的有载分接开关振动信号分析方法迅速发展，相关学者对此进行了研究，取得了一定的进展。文献[2]利用VMD 方法对变压器信号进行去噪，采用模态分解技术提取信号的模态分量特征，并通过小波包阈值处理获得最佳分解层数,实现振动信号模态分解重构，此方法能够提升信号分析效果。文献[3]采用时频特征分析方法进行振动信号识别，通过自适应遗传算法对模态函数分量进行分解，构建BP 神经网络模型实现变压器故障信号识别，采用能量熵实现能量熵振动信号的模态分解，能够有效降低信号分解用时。

在实际工作环境下，对分接开关切换过程进行振动信号采集时不可避免地会混合变压器本体的振动，影响后续故障识别过程的准确率，该文从使用固有模态函数进行信号重构的角度，对经验模态分解过程中的分段处理、模态混叠抑制、重构分量选择等问题开展研究，并利用分接开关故障仿真模拟台数据进行了验证。

1 有载分接开关振动信号去噪处理

当分接开关工作时，接收的振动波形y(t)由分接开关振动信号x(t)和本底噪声n(t)组成，即：

当分接开关未工作时，x(t)=0，接收到的振动波形由变压器本底振动噪声n(t)决定[4]。对本底噪声进行数量为L的IMF 分解，可得：

式中，E1是第一个IMF 分量的能量，β和ρ是拟合参数，其值由EMD 筛选迭代次数决定，Ej代表纯白噪声的能量。β和ρ的具体值可以通过对有载分接开关未工作时变压器的本体背景振动信号进行采样后由IMF 拟合得到。典型地，可以取β=0.72、ρ=2.0。

当分接开关工作时，同样可对y(t)进行数量为L的IMF 分解，可得：

在离散采样情况下，可以表示为：

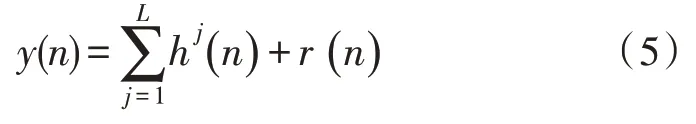
为了降低本底噪声对各个IMF 分量的影响，可以采用分段阈值滤波处理方法。首先，将各个IMF分量按照波形过零情况进行分段，得到不同的波形区间然后按照区间对各个IMF 使用阈值滤波：

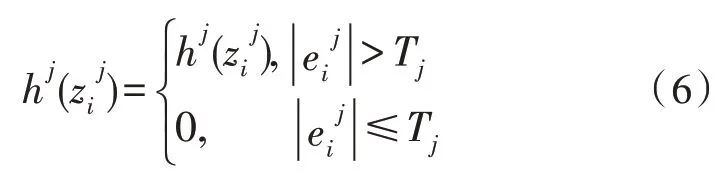
式中，C代表常数，N为波形点数，为仅有噪声情况下第j个IMF 分量能量的估计值。

使用一组在分接开关故障模拟台上采集的波形数据，来分析分接开关未工作时的纯噪声波形与分接开关工作时的混合波形的IMF 能量分布，如图1 所示。可以发现，纯噪声情况下各个IMF 的能量呈对数-线性分布，而混合波形由于存在分接开关振动信号，从第3 个IMF 分量开始与纯噪声情况存在明显偏离值。

图1 不同条件下的IMF能量分布

2 基于时频特征的故障识别

在对开关振动信号进行分解时，由于实际工程中振动信号普遍存在模态混叠现象，造成分解结果缺乏稳定性和唯一性，从而导致信号时频分布不均匀。因此，为了抑制模态混叠现象[5]，采用掩膜方法对降噪过程的经验模态分解进行改善[6-7]。具体过程如下所示：

Step1：对信号和噪声混合波形y(n)，创建一个改进的掩膜信号s(n)，分别与原来的信号进行运算，如下所示：

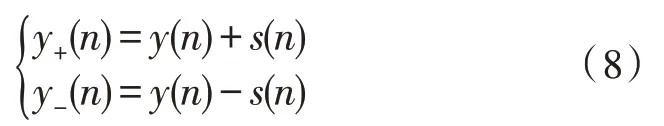
Step2：对y+(n)、y-(n)进行EMD 分解，得到第j个固有模态函数和取平均值后得到添加掩膜的固有模态函数[8-11]：

掩膜信号的构造方法[12]如下：

式中，a1(i)为的包络幅值，f1(i)为使用Hilbert 变换法估计的的瞬时频率[14-15]。

对振动波形的各个IMF 进行阈值滤波处理后，通过选取若干个IMF 进行波形重构，得到降噪信号。IMF 的选取可以采用相关系数法，设置相关系数门限rh，分别计算原始信号与第j个IMF 的相关系数ρj，保留相关系数大于rh的分量。

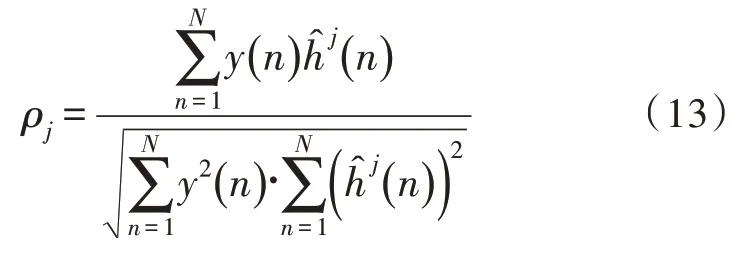
rh的取值与具体的信号形式有关，一种典型的设置方法是取最大相关系数与最小相关系数平均值的倍数[16]：

式中，α为大于1 的常数，文中取1.5。

使用时频图和卷积神经网络对降噪后的振动波形进行故障识别。常见的时频图生成方法有短时傅里叶变换、小波变换、Wigner-Ville 分布等方法，文中采用短时傅里叶变换，其中DFT 长度为512，加窗方式为海明窗，样本重叠率为75%。使用卷积神经网络对生成的时频图进行类型识别，该网络包含3 个卷积层、3 个池化层和1 个全连接层，采用了最大值池化方式与尺寸为5×5 的卷积核。

3 实验对比

3.1 实验数据获取

为了获取故障数据，搭建了有载调压开关模拟实验平台，模拟分接开关在变压器油箱中的工作环境，如图2 所示。该模拟台采用CMIII-500Y/72.5C-10193W 型开关,能完成分接开关逐级档位切换。振动信号采集系统采用DEWE3-RM16 系统，可同步采集振动及电流信号。实验中将振动传感器设置于分接开关顶部，采用100 kHz 采样率进行数据采样。

图2 有载分接开关故障模拟台

将有载分接开关故障模拟台分别设置为正常状态和内部弧形板松动状态，每种状态各获取200 组测试数据。由于故障模拟台的环境较为理想，获得的分接开关切换引起的振动信号受其他因素干扰较小[17]，为了更接近真实环境，按照不同的信噪比对采集的信号分别添加宽带白噪声，作为噪声和振动混合信号。一组正常状态下获得的纯信号及混合波形（信噪比为5 dB）如图3 所示。

图3 一组正常状态下获得的纯信号波形及混合波形

3.2 去噪效果对比

分别对未进行降噪处理和按照该文所述方法进行降噪处理的数据进行基于时频特征的故障识别，对比识别准确率。图4 显示了分接开关内部弧形板松动状态下的信号固有模态分解图，可以发现随着IMF 序号的增加，IMF 分量的频率范围逐渐降低。

图4 分接开关内部弧形板松动状态下的信号固有模态分解图

图5 显示了该信号各个IMF 分量与原始信号的相关系数，可以看到，对于所分析的信号，第3 和第4个IMF 具有较大的相关系数，因而也包含了更多的振动信号信息。

图5 IMF分量与原始信号的相关系数

设置相关系数门限为0.35，使用相关系数大于门限的IMF 对该信号进行重构，得到降噪的信号如图6 所示。

图6 降噪处理后的波形图

按照上述步骤在不同信噪比下进行计算，对重构处理后的信号减去添加的噪声得到降噪后的纯信号部分，计算处理后的信噪比，如表1 所示。

表1 降噪处理前后的信噪比对比

表2 显示了分别使用未降噪和已降噪的信号进行分接开关故障识别的结果。

表2 降噪处理前后的识别准确率对比

4 结束语

该文研究了一种基于固有模态函数重构的有载分接开关信号识别方法，通过对混合信号的模态分解、模态阈值滤波、信号重构、时频分析和卷积神经网络故障识别，可以获得有效的降噪增益以及识别准确率的提升。