基于双目视觉的标定和立体匹配的研究

杨记鑫，胡伟霞，赵杰

（成都理工大学工程技术学院，四川乐山 614000）

随着计算机技术和机器视觉技术的不断发展，双目视觉技术的应用越来越广泛。双目测距是采用左右两个相机拍摄的图片，依据双目视差原理计算得到图片的深度信息的一种技术[1]。

双目测距通常由标定、校正、匹配三部分组成。由摄像头标定方法得到摄像头的结构参数，再用这些结构参数对图像进行校正，然后输入到匹配算法中，计算得到视差。其中，相机的光学像差对标定精度有很大影响，像素匹配算法决定测量的准确性。文献[2]提出了两步标定法，该方法中大部分参数是采用线性直接求解，计算速度较快，但是畸变模型较为简单，精度较低；文献[3]提出了一种标定算法，该方法没有考虑相机切向畸变；文献[4]提出了一种改进的张正友方法；文献[5]提出的DLT 方法，计算较大，标定精度相对较高；此外文献[6]提出了基于人工智能的标定算法。匹配部分通常采用基于深度学习的算法。文献[7]采用多个BRIEF 描述子实现立体匹配，效果较好；文献[8]提出的AANet 算法，匹配度较低；文献[9]提出的CTFNet 算法，匹配度较高，但是运算量较大，运算时间长。文中主要研究了相机标定和立体匹配的算法。

1 双目立体测距原理

双目立体视觉测距系统主要由两个位于同一水平线的摄像头组成。两摄像头型号、批次完全相同，有公共的可视区域，依据三角相似的数学方法进行距离测量，测距原理如图1 所示[10]。O1和O2为摄像机两个摄像头的光心，距离为B，空间里某物体上点P，在左右两个摄像头成像平面所成的点分别为P1(x1,y1) 和P2(x2,y2)。假设摄像头焦距为f，由三角形相似原理可得：

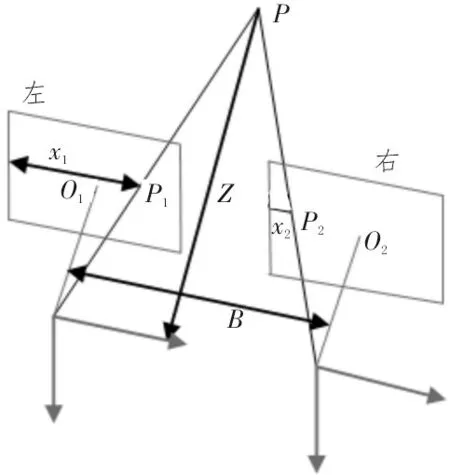
图1 双目测距原理

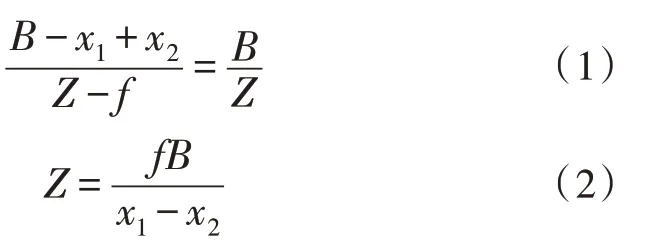
为了方便模型分析，设某P点在空间坐标系中的坐标为(X,Y,Z)，在相机坐标系中的坐标为(X′,Y′,Z′)，图像坐标系表示为(x,y)，像素坐标系表示为(u,v)，从空间坐标系到相机坐标系，需要进行平移和旋转，即：

空间点投影到平面上，满足投影法，可得出相机坐标系到图像坐标系，即：

图像坐标系的原点为相机光轴与成像平面的交点，单位是mm，像素坐标系是以像素阵列中第一个点为原点，单位是pixel，可得图像坐标系到像素坐标系，即：

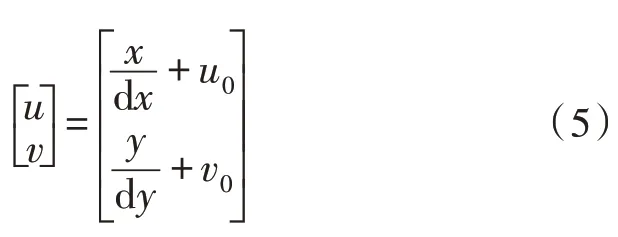
由以上式可得：

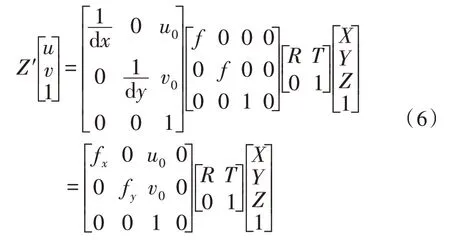
式（6）中的矩阵是由摄像机的参数确定的，可以通过标定方法获取。此外，摄像机还存在径向、横向、波透镜畸变等，对实际测量有很大的影响[11]。

2 相机参数标定算法

常用的张正友标定法主要是拍摄标定板在不同视角下的多幅图像，通过对应特征点的数学算法求出相机参数，该算法忽略切向畸变的影响，有很大的误差。基于BP 神经网络的标定法[12]主要由输入层、隐层以及输出层，通过反向传播不断学习得出输出与输入的关系，有非常强的非线性拟合能力，但是学习效率低，收敛速度慢，在初始权值和阈值的选择上随机性强，网络梯度下降方向上也比较随机，容易陷入局部最优解[13-14]。该文根据相机成像模型提出了一种改进型的BP 网络标定方法，采用遗传算法得到BP 网络的初始权值和阈值，如图2 所示。

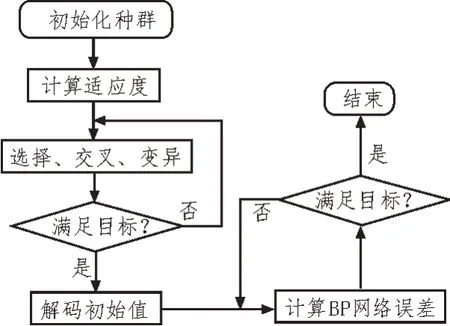
图2 遗传BP算法

1）初始化种群。对种群进行编码操作。编码方式采用实值编码方式，种群规模设置为60。

2）适应度函数。结合BP 网络的算法，需要满足适应度值为非负的要求，也为了后续计算方便，该文采用的适应度函数为：

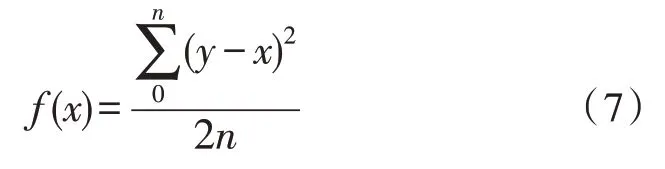
式中，x为样本值，y为对应的期望值，n为样本个数。

3）计算得到种群个体的适应度值，进行选择、交叉和变异操作。个体选择采用适应度比例方法，个体选择的概率为：

采用单点交叉的方式，交叉概率设置为0.8，采用基本位变异的方式，变异概率设置为0.005。迭代次数设置为60 代。

4）从种群中选取最优值，作为BP 神经网络的初始权值和阈值去训练网络。BP 网络为三层结构，输入层、隐含层和输出层神经元的个数分别是20、12和40，为了防止陷入局部最优解，该文采用自适应的学习率η满足：

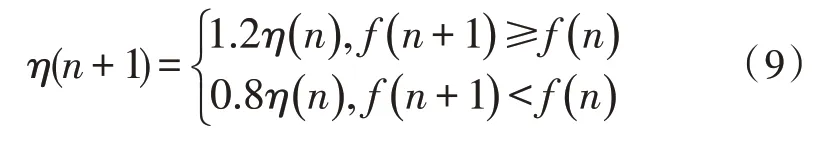
其中，输入层到隐含层调节系数为0.5，隐含层到输出层调节系数为0.2，计算网络的输出误差，多次训练网络，直到满足要求。

5）采用训练好的遗传BP 神经网络实现相机的参数标定。

3 立体匹配算法

依据双目测距原理分析可知，求出左右摄像头拍摄的每幅图对应点的视差，即可得到图像的深度信息。立体匹配通常包括匹配代价、代价聚合、视差计算，该文提出了一种改进的CNN 结构实现立体匹配算法，如图3 所示。

传统的代价匹配选用局部区域进行计算。首先提取特征角点，对结果进行修正，将小于特定值的数值修改为0，只通过对应两幅图的边缘特征计算实现代价匹配。主要方法如下：左视图保持不动，右视图移动，设置最大的视差，对两幅图进行特征提取计算匹配代价，采用3×3、步长为2 的卷积核进行采样、均值池化、数值修正，连续运行3 次。为了提升运算速度，在卷积网络中加入残差模块，可快捷传递到底层。

为了充分利用左右两图的信息，代价聚合是将两个代价向量叠加成新的向量，特征信息从2D 变为3D，使用3×3×3、步长为2 的卷积核进行采样，该卷积运算量较大[16]。该文结合间接卷积算法对代价聚合进行改进。

按照宽和高将一个大的卷积计算拆分为若干个小的卷积计算，虽然在划分的过程中计算总量不变，但计算小矩阵时访存局部性更好，可以借由计算机存储层次结构获得性能提升。每个小的卷积块再使用Im2col 法将三维张量转换为二维矩阵，计算方法如下：

式中，input 是输入的尺寸，kernel 是卷积核尺寸，stride 是步长，output 是输出的尺寸。

在Caffe 中利用已经优化好的GEMM 库来为各个平台加速卷积计算，最后再采用Col2im 将二维矩阵转换成三维矩阵输出。

最后，采用softmax 函数进行视差预测[9]。

4 实验与结果分析

4.1 标定算法实验

实验所采用的标定板是9×6 的棋盘格，棋盘方格为40 mm×40 mm，使用两个USB 工业相机采集20组不同角度的标定图片，采用Harris 法进行特征点提取，然后进行标定。

另取一部分点进行测试，并与张正友标定法和BP 网络标定法对比，测试结果如表1 所示。与BP 算法[13]相比，该文提出的基于遗传BP 网络算法的标定精度有所提升。

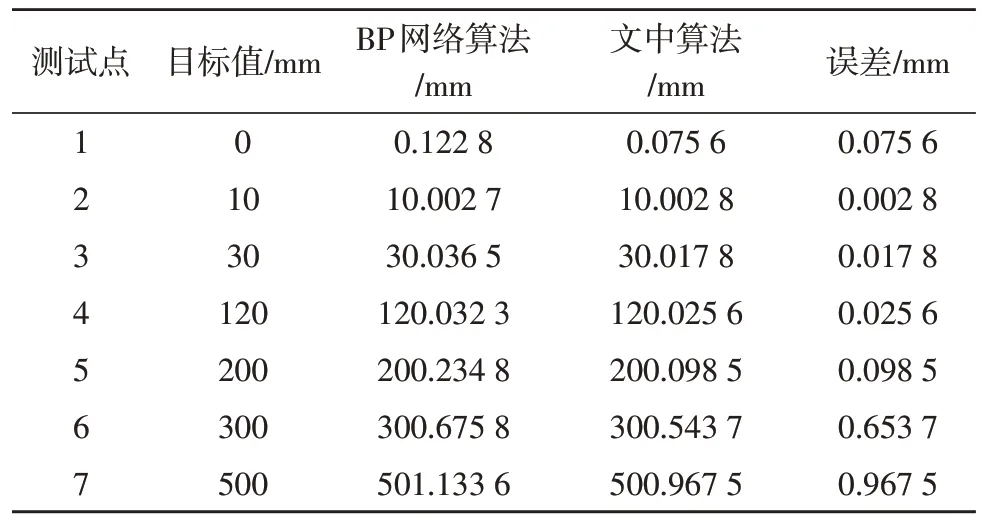
表1 标定方法测试对比

4.2 匹配算法实验

选取Middlebury 数据集的数据进行测试，将文中的算法与CNN 算法[15]、CTFNet 算法[16]进行对比，如图4 和表2 所示。

图4 匹配效果对比

表2 立体匹配算法测试对比

从图4 可以观察到，CNN 算法相对模糊，立体匹配效果较差；CTFNet 算法匹配效果较好，但图中出现无纹理和弱纹理区域。该文提出的算法，细节处理更加精确。由表2 可知，该文的算法在平均误差方面比参考的CNN 算法和CTFNet小，并且运行时间短，该算法可以很好地处理立体匹配。

5 结论

该文针对传统的标定算法进行改进，提出遗传BP 的标定算法，该算法主要利用遗传BP 网络的动态学习和不断修正的优点实现摄像头参数的标定，与传统的张正友标定和参考的BP 网络标定相比，精确度都有所提升。该文还对立体匹配算法进行改进，残差网络和数据修正可使运算时间减少，间接卷积的方式可使3D 卷积过程运算量减小，该算法可在保证精确度的前提下，缩短运行时间。