一种适用于条带SAR 的快速后向投影算法

刘财安，李 飞，张 衡

（1.中国科学院空天信息创新研究院，北京 100190；2.中国科学院大学，北京 100049；3.中国科学院大学电子电气与通信工程学院，北京 100049）

合成孔径雷达(Synthetic Aperture Radar,SAR)具有全天时、全天候的对地观测能力，被广泛应用于灾害监测、海洋研究等领域[1-3]。目前SAR 成像算法主要分为频域和时域两大类，频域算法的成像效率较高[4-7]，然而该算法无法有效处理非线性轨道模型[8-9]。相比之下，时域算法能够实现任意轨道模型的精确成像[10-11]。时域算法的典型代表是后向投影(Back-Projection,BP)算法，由于该算法需要逐点计算，其时间复杂度高达O(N3)。为了提高BP 算法的成像效率，各类快速算法被相继提出[12-14]，并将时间复杂度降到O(N2logN)。然而这些快速算法大多只针对聚束SAR 成像，少有针对条带SAR 的研究。

为了实现条带SAR 的高效率精确成像，该文根据条带SAR 的特性，提出一种基于线性成像网格的FBP 算法，并通过点目标仿真和实测数据实验，验证了算法的有效性。

1 条带SAR的子孔径合成分析

BP 算法的核心思想是将每个孔径对应的雷达回波数据后向投影到所有的像素点上，但在实际成像中，相近孔径的雷达回波数据具有相似性。因此没有必要将每个孔径的雷达回波数据后向投影到所有的像素点上，BP 快速算法正是通过一级或多级子孔径合成的方式来降低相近孔径间的数据冗余，以提高成像效率。

基数为4 的子孔径合成示意图如图1 所示，通过以“新”子孔径为中心建立的局部极坐标系和角域划分，将“旧”子孔径yi合成一个“新”子孔径y。

时域成像的关键就是积分孔径内的相干累加[15]，因此需明确每个像素点的积分孔径。聚束SAR 的子孔径合成如图1(a)所示，聚束SAR 的天线波束被控制指向相同的成像区域，即成像区域中所有像素点均对应相同的积分孔径。因此，聚束SAR 在子孔径合成前后，每个像素点的积分孔径均保持不变。条带SAR 的子孔径合成如图1(b)所示，条带SAR 的天线波束指向始终保持不变。在子孔径合成前，每个“旧”子孔径的波束只能覆盖成像区域的一部分。在子孔径合成后，“新”子孔径包含所有“旧”子孔径的信息，其波束能够覆盖整个成像区域，那么成像区域中每个像素点的积分孔径范围变大。因此基于BP快速算法的条带SAR 成像，需要动态确定每个像素点的积分孔径。

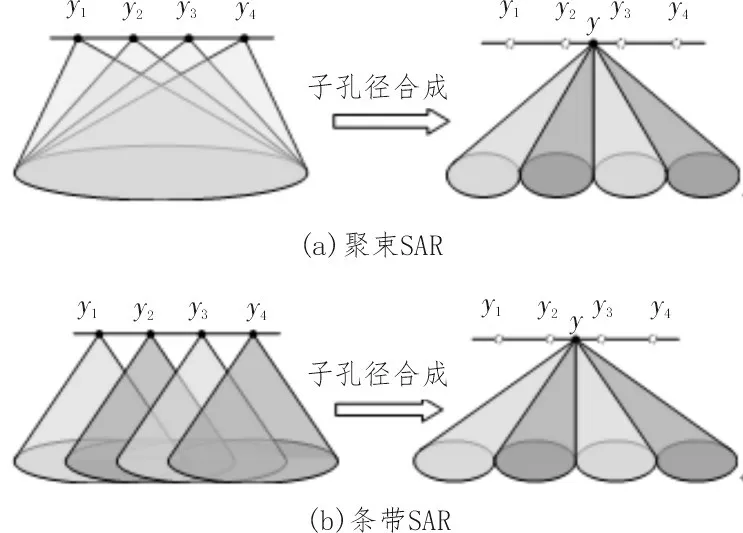
图1 基数为4的子孔径合成示意图

在子孔径合成中，每个像素点的角域波数带宽与该像素点的有效合成孔径长度LP有关，即，其中为最大距离波数[12]。假设“新”子孔径的长度为Ls，则聚束SAR 在成像区域中每个像素点的有效合成孔径长度均为Ls，故其每个像素点的角域波数带宽均为。虽然条带SAR在成像区域中每个像素点的有效合成孔径长度互不相同，但是存在某些像素点的有效合成孔径长度为Ls，即其最大角域波数带宽也为。因此聚束SAR 和条带SAR 的角域采样率应该相同，然而条带SAR在子孔径合成后的成像区域变长，如果将BP快速算法直接应用于条带SAR，其角域会出现欠采样的现象，从而导致角域波数谱混叠，使得图像模糊不清[16]。

2 基于改进算法的条带SAR成像

2.1 改进的快速BP算法

目前，大多数BP 的快速算法的子孔径合成都是工作在极坐标系下，需要进行频繁的极坐标系与直角坐标系转换，而坐标系的转换需要角域和距离二维插值，会影响成像效率和成像质量[17-18]。Block-FFBP[13]通过距离向上的分块处理，简化了直角坐标系与极坐标系之间复杂的转换，然而其分块特性、逐级增长的内存空间以及必须采用插值核插值[14]，严重影响成像效率。该文借鉴Block-FFBP 距离向分块处理的思想，提出一种基于线性成像网格的FBP 算法，每个网格的距离向宽度为一个像素，方位向宽度取决于子孔径合成中的方位向采样间隔。该文将网格的中心称为控制点，控制点与孔径的连线称为光束中心线，如此便能将Block-FFBP 中的块转换为控制点，避免分块操作导致的低效率成像。

改进的FBP 算法分为子孔径合成阶段和全分辨率成像阶段，两个阶段的成像网格在距离向上的控制点数相同。这里将子孔径合成阶段的成像网格称为降分辨率成像网格全分辨率成像阶段的成像网格称为全分辨率成像网格(xm,yn)。假设SAR 图像的像素为M×N，子孔径合成中控制点的方位向采样间隔为D，则全分辨率成像网格的尺寸为M×N，降分辨率成像网格的尺寸为

为了方便解释，该文用Qi表示第i个原始孔径，每个原始孔径对应接收回波信号的实际雷达位置，表示子孔径合成后的第j个子孔径，和P(m,n)分别表示降分辨率和全分辨率成像网格中的控制点。

子孔径合成阶段，假设每相近的Ns个原始孔径合成一个子孔径，对于条带SAR，合成后的每个子孔径覆盖的成像区域变大。由于其成像区域中每个控制点的积分孔径互不相同，这里用来判断原始孔径Qi是否在控制点的积分孔径内。基数为Ns的第j个子孔径合成示意图如图2 所示，其成像区域中控制点与原始孔径Qi(xi,yi,zi)和子孔径之间的距离Ri和Rsj分别为：

图2 基数为Ns 的第j 个子孔径合成示意图

假设雷达的飞行轨迹与方位向平行，则有xi=xsj,zi=zsj，将上式联立可得：

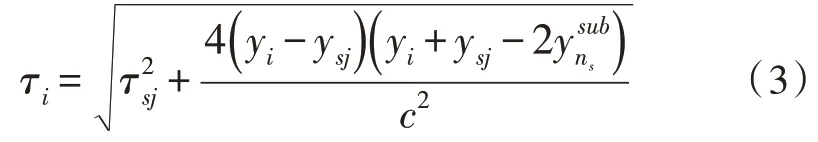
则第j个子孔径在控制点处的雷达回波值为：

其中，src(τi;Qi)表示第i个原始孔径中双程时延为τi的雷达回波值，ss(τsj,ns;)表示第j个子孔径中成像网格控制点方位为ns、双程时延为τsj的雷达回波值。在子孔径覆盖的成像区域中，每个控制点会对应一个雷达回波值，因此每个子孔径对应的雷达回波数据是一个数据矩阵。

全分辨率成像阶段，使用一系列子孔径对应的雷达回波数据矩阵获得最终的全分辨率图像。全分辨率成像网格中控制点P(m,n)的成像如图3 所示，可以看出控制点P(m,n)的积分孔径为假设降分辨率成像网格中控制点的方位向采样间隔为D。首先计算积分孔径内的每个子孔径Qsub到控制点P(m,n)的双程时延，然后根据时延插值得到每个子孔径在处的后向投影值，最后将对应的后向投影值相干累加，即可得到控制点的像数值，如式（5）：

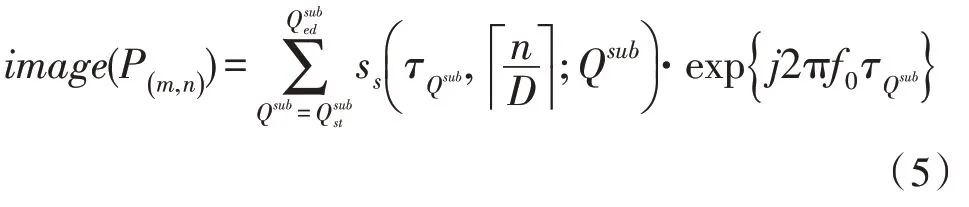
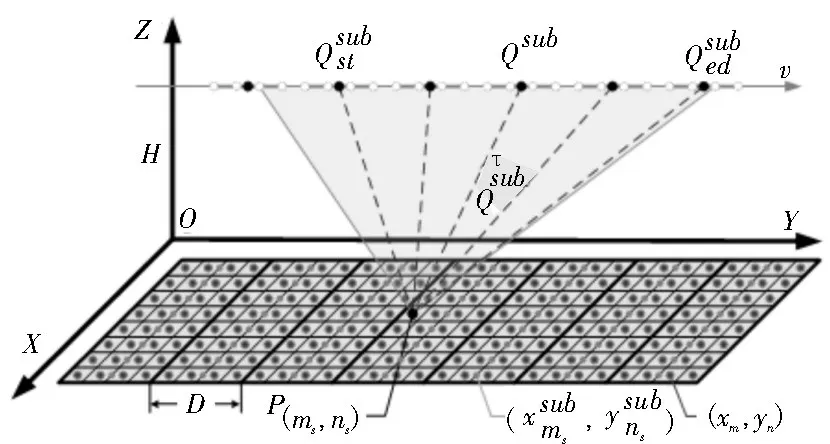
图3 控制点P(m,n) 的成像示意图

该算法不再使用局部极坐标系的子孔径合成，而是直接将成像网格建立在全局直角坐标系中，即每个子孔径合成都在同一个直角坐标系中进行，因此该算法无需坐标系的转换且易于并行化。

2.2 针对条带SAR的参数计算

由于条带SAR 在子孔径合成前后的积分孔径和成像区域会发生改变，因此该算法针对条带SAR 成像还有两个重要的参数需要计算，分别是控制点的积分孔径和降分辨率成像网格中控制点的方位向采样间隔。

控制点的积分孔径就是波束能够覆盖到该控制点的所有孔径，故控制点积分孔径的计算等价于孔径波束覆盖宽度的计算。孔径波束的覆盖宽度与天线波束斜视角θsq、天线波束方位向宽度θbw和孔径长度LQ有关。孔径Q的波束覆盖示意图如图4 所示，假设飞行轨迹与方位向平行，R0为孔径到控制点的最短距离，La为天线波束方位向覆盖宽度。令孔径Q和控制点P的方位坐标为yQ和yP，则当控制点P满足式（6）时，孔径Q的波束能够覆盖到该控制点。

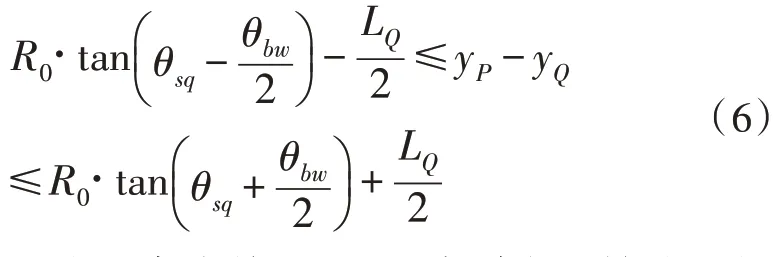
其中，子孔径合成前后的LQ分别为原始孔径长度和子孔径长度。

降分辨率成像网格中控制点的方位向采样间隔取决于控制点的方位波数大小，方位波数κa与控制点的有效孔径长度LP呈线性关系。如图4 所示，假设该图处于子孔径合成阶段，此时子孔径长度LQ=Ls，子孔径波束的方位向覆盖宽度为La+Ls。由于条带SAR 固定的天线波束指向，其任意控制点P的有效孔径长度LP均不超过子孔径长度Ls，即LP≤Ls。以子孔径覆盖宽度的中心为原点建立局部直角坐标系，令Y轴为方位坐标轴。则控制点的有效孔径长度LP与其方位坐标y之间的关系为：

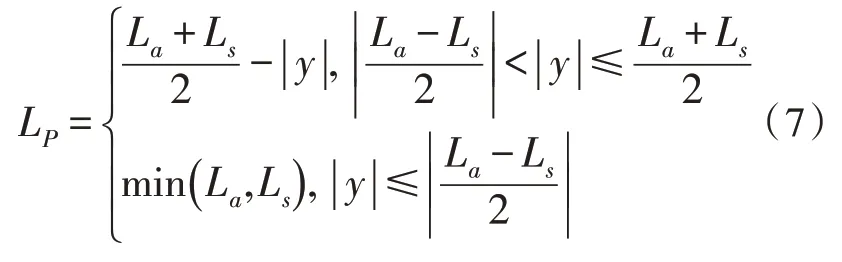
图4 孔径Q 的波束覆盖示意图

子孔径覆盖区域中方位波数κa与控制点方位坐标y的关系如图5 所示。图中控制点的方位波数呈等腰梯形分布，只有位于中间区域的控制点的方位波数最大，且整个覆盖区域的方位波数总和为La∙Ls。假设该子孔径由Ns个原始孔径合成，为了避免方位向出现欠采样现象，覆盖区域中的方位向采样间隔D应满足式（8）：

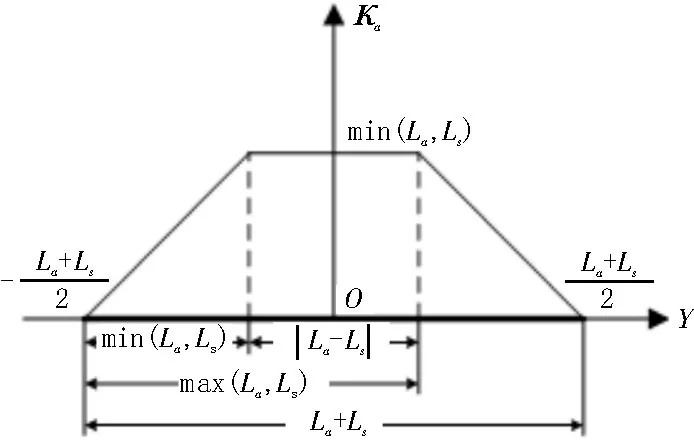
图5 方位波数与控制点的关系示意图

并将子孔径覆盖区域中的方位向采样间隔应用于整个降分辨率成像网格。

3 实验结果与分析

为了更直观地展示改进FBP 算法的有效性，选择一个X 波段机载条带SAR 进行相关实验，具体参数如表1 所示。分别使用改进FBP 算法和BP 算法进行点目标仿真和实测数据实验，并在成像质量和成像效率两个方面进行比较分析。

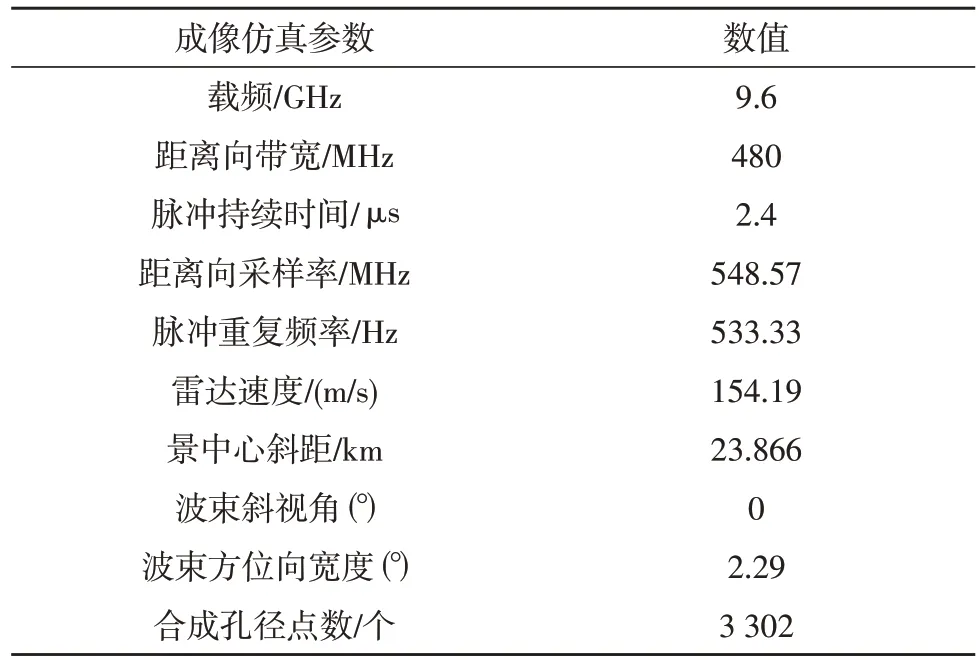
表1 X 波段机载条带SAR仿真参数

3.1 点目标仿真实验

在仿真场景中设置9 个点目标，点目标的距离向和方位向间隔均为50 m，如图6 所示。首先得到尺寸为2 048×3 994 的仿真回波数据矩阵，然后分别使用不同基数的改进FBP 算法进行成像，并将成像结果与BP 成像进行对比，这些算法的点目标成像结果基本一致。

图6 点目标分布示意图

然后对编号为5 的点目标进行性能分析，如图7所示，展示了基数为50 的改进FBP 算法与BP 算法在该点目标处的成像效果对比。如表2 所示，记录了不同基数下点目标在距离向和方位向上的峰值旁瓣比(Peak Sidelobe Rate,PSLR)和积分旁瓣比(Integration Sidelobe Rate,ISLR)。从中可以看出，在距离向上，改进FBP算法的PSLR 和ISLR均优于BP算法约0.1 dB，两者的距离向剖面图也基本保持一致。在方位向上，改进FBP 算法的性能指标稍低，其PSLR 和ISLR高于BP 算法约0.2 dB 和1.8 dB。但从方位向剖面图来看，两者大致吻合，即两种算法的实际成像效果相差不大。因此改进FBP 算法具有较好的成像质量。

图7 点目标的目标分析

表2 点目标性能对比

接下来比较改进FBP 算法和BP 算法的成像效率，将这两个算法以单线程的方式运行在同一环境下（运行环境：Intel(R) Core(TM) i7-8750H CPU@2.20 GHz,RAM 32 GHz）。BP 算法的运行时间为2 342.2 s。改进FBP 算法在不同基数下的运行时间，如表3 所示。可以看出，基数在附近的运行时间最短。在实际成像中，一般取基数，此时改进FBP 算法的成像效率相较于BP算法显著提高。

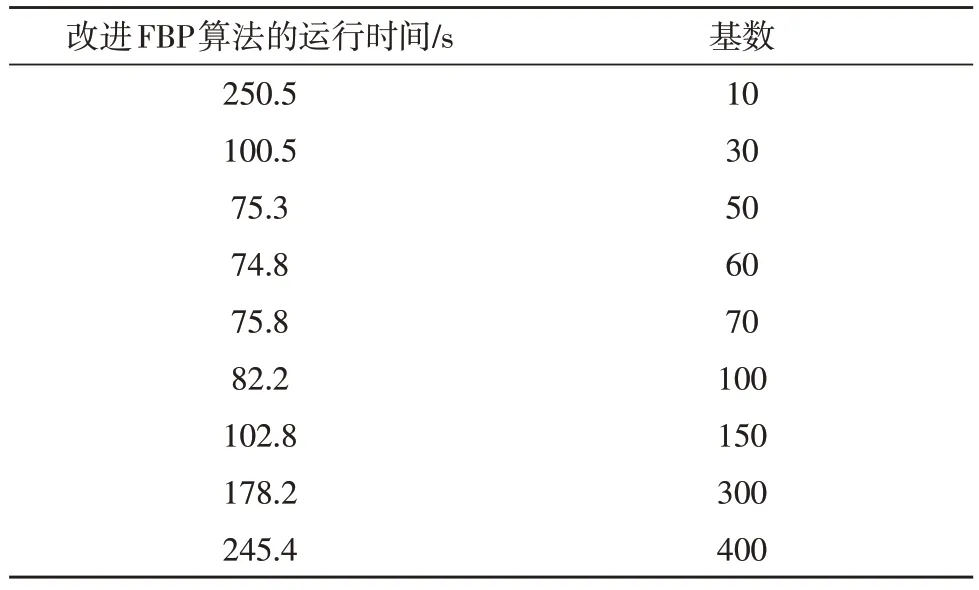
表3 改进FBP算法在不同基数下的运行时间

3.2 实测数据实验

利用实测数据验证改进FBP 算法的有效性，真实数据和成像的大小均为4 096×4 096 的矩阵。经过实验对比，改进FBP算法在方位向上的局部成像效果稍差些，但整体的成像效果几乎一致。成像效率方面，两种算法的运行时间分别为75 min 和2.27 min，改进FBP 算法的成像速度约为BP 算法的33 倍。

综上所示，通过点目标仿真和实测数据实验表明，相对于BP 算法，改进FBP 算法能够在保证成像质量的同时显著提高成像效率。

4 结论

该文指出了聚束SAR 和条带SAR 在子孔径合成中的区别，条带SAR 在子孔径合成中存在孔径积分变化和角域欠采样的现象。如果将BP 的快速算法直接应用于条带SAR，会导致所成图像的方位模糊。为了实现条带SAR 的高效率精确成像，该文借鉴Block-FFBP 距离向分块处理的思想，提出一种基于线性成像网格的FBP 算法，将Block-FFFBP 中的块转换为控制点，并将成像网格建立在全局直角坐标系中，一方面能方便计算积分孔径在子孔径合成前后的变化，以及通过成像网格中控制点的方位向采样间隔调节成像网格中的控制点数，避免条带SAR 成像的方位模糊，另一方面有效地避免了子孔径合成中坐标系的转换。

通过点目标仿真和实测数据实验，证实了该算法不仅能获得与BP 算法大致相同的成像质量，还能显著提高成像效率，具有比较高的工程应用价值。