碾压混凝土坝施工期温度应力数值模拟技术进展

彭文明

(中国电建集团成都勘测设计研究院有限公司勘测设计分公司，四川 成都 610072)

1 概 述

1.1 碾压混凝土筑坝技术的特点

碾压混凝土(RCC)筑坝技术是从20世纪60年代开始试验研究[1-2]的。该项技术的应用改变了常态混凝土施工方法，用振动碾压机可在层面进行振动碾压，大仓面施工。具有节省水泥用量、施工更简便、造价更低廉、坝体少分缝、大仓面施工、工期缩短等优点[3]。由于RCC采用大仓面的薄层浇筑施工方法与柱状块浇筑施工明显不同，因此，混凝土水化热减少，散热条件与常态混凝土浇筑也有所不同。

RCC单位体积的水泥用量较常态混凝土减少[4]，水化产生热量少，对温度控制有利。但是，RCC坝冷却水管埋设不方便，由于连续升程碾压，散热表面积经常比常态混凝土坝施工小，或散热时间少，这是温度控制方面的不利条件。

总之，由于筑坝方法的改变而引起的一系列技术问题需要进行研究。坝越高，引起的相关问题越复杂；碾压混凝土坝的温度场、温度应力问题和温控方法是必须重点研究的问题。

1.2 碾压混凝土坝温变效应仿真分析的难度

由于RCC坝体都是通过分层浇筑的，并且在浇筑的过程中需要经历若干个寒夏，所以在施工的这个过程中会对于坝体的温度场及其应力场产生重要的影响。为了能够正确地掌握混凝土坝的温度场及其应力场，必须对该大坝的施工流程进行合理的仿真和分析。

目前碾压混凝土坝仿真计算主要有以下几个难题[5-7]：

(1)浇筑层数多。RCC大坝通常都是进行分层浇筑、碾压施工的，在建设和施工的过程中由于每个浇筑层的混凝土时间不同，相应的弹模和徐变度也不同，因此在有限元模拟实际建设施工的过程中，必须针对每一个浇筑层进行网格划分。其中的浇筑层水平面积尺寸比较大，但是每层厚度比较薄，通常只有0.3 m。混凝土在浇筑仓面的顶面朝空气散热，底面向接触的基岩或已浇混凝土传热，不同浇筑层因龄期的不同又有不同的水化热。因此，浇筑层沿竖直方向温度梯度以及应力梯度一般都较大，为了获得足够的计算精度，各层都须采用比较小的计算网格。若层数较多，因单元网格太多，线性方程组阶次高，导致计算机容量要求大、计算时间长。

(2)计算步长小。由于早龄期混凝土的弹性模量、徐变度和绝热温升等随龄期剧烈变化，需采用较小的时间步长，以获得所需的计算精度。取时间步长为Δτ=0.5 d的话，一年将有730个计算步，如果工期3 a，将有2 190步计算。如果还要考虑阳光和每日气温的变化影响，时间步长还应减小到1 h左右，则工期3 a就会有2.6万步。温度场和应力场在每步都需要计算，进行大型线性方程组计算对计算机提出很高的要求。

(3)碾压混凝土坝通常在水流方向通仓浇筑，在坝轴方向分为多个仓面，在垂直方向上模板高度为一个连续碾压单元。所以，左右两仓交错上升，在两仓的交界处，施工过程中新老混凝土之间存在单元连接问题；另外，岩石的网格一般比较大，碾压混凝土在浇筑过程中，与两侧岩石的连接也存在问题。

(4)水管冷却模拟计算有难度。冷却水管一般半径为1～2 cm，水管周围须采用较密集的计算网格，通常单元尺寸为厘米级，虽然可往外逐步扩大划分单元尺寸，但单元和节点总数还是很多，对计算机硬件要求很高，甚至无法进行计算。

综上所述，对碾压混凝土采用常规有限元方法仿真分析时，单元和节点多，计算步长小，计算工作量非常大，几乎无法实现。

2 多层材料的并层模拟技术

2.1 并层算法

混凝土结构到一定浇筑龄期，相邻浇筑层材料属性相差不大，可以对其进行并层[8-9]。并层算法的核心思想是：施工一定龄期后，把混凝土材料属性接近的多层已浇混凝土并成一层单元，用大单元合并原先的小单元，合并后单元材料属性采取一定方法取均化值。

在混凝土浇筑过程中，将浇筑块划分为4个区域(如图1所示)。在新浇筑区域R1中，沿浇筑厚度方向存在温度和应力的变化梯度比较大，可将每个浇筑n层升程直接划分成n层单元。下面区域R2～R4，每浇筑层沿厚度方向呈现温度增量以及应变增量为线性分布，或趋于平缓，甚至趋于相同，可把原来一个升程浇筑的n层单元进行合并为一层单元，或把几个升程的浇筑层再合并为更大的复合并层单元，从而减小有限元计算规模。

图1 并层算法分区示意

并层算法在较好解决了计算分析规模过大的问题，但单元材料均质化将带来一定误差；另外，随着浇筑层升高，单元需要多次并层重构，处理起来比较麻烦，且每次扩网都将引起单元能量的丢失或增加[10]，导致误差。

2.2 等效弹模法

等效弹模法[11-12]是一种处理多层材料的方法，其思想是把多种各向同性的材料等效成一种各项异性的材料，根据各项异性材料的计算方法对结构进行分析，得到单元内的平均应力和平均应变，再通过修正可获得每层材料的应力和应变值。

对图2所示的单元，单元内含有n种材料，每种材料均为各向同性。对于第i种材料，其弹性模量为Ei，泊松比为νi，层厚度为ti(相对厚度，∑ti=1)。

图2 多层材料示意

单元内的平均应力为σ，平均应变为ε；每一层内应力为σi，应变为εi。把整个单元材料等效成一种材料[13]，该材料各向异性，其材料属性为Ex，Ey，Ez，Gxy，Gyz，Gzx，vxy，vyz，vzx，然后用各项异性材料的方法求出单元内的应力和应变，所得到的应力和应变是单元内的平均应力σ和平均应变为ε，它们与每一层材料的应力σi和应变εi有如下关系，即

(1)

式中，si、ei均为附加修正项。

与并层算法一样，等效弹模法能解决计算规模大的问题，而且在求解等效各项异性材料属性时考虑了不同层材料的差异；但是该方法把不同层的材料参数均匀化，对于材料参数相差不大的多层材料，其计算精度可得到保证；如果材料参数相差太大，沿层平面方向的位移误差将很大。

2.3 等效连续模型

刘光庭等[14]、王宗敏等[15]分别提出基于位移的等效连续模型。与等效弹模法类似，该模型中把含多个碾压层的单元等效成一种材料，所不同的是该模型不考虑碾压层之间的差异性，而是以模拟相邻层之间的由于施工间隔造成的弱面作为重点。等效连续模型也能够加大网格尺寸，不过主要针对结构分析；而且忽略了单元内各碾压层之间材料属性的差异性，将造成一定的误差。

2.4 浮动网格法

浮动网格法根据混凝土材料与龄期之间的关系，将浇筑一定时间后的若干层网格进行浮动，将薄层网格进行浮动成为大网格[16]。使用浮动网格法，即使碾压混凝土结构的碾压层有上百或几百层，但随着坝体的升高，下面的各浇筑层浮动为较大的网格(如图3所示)，网格数大为减少，因而可大大减少结点数，从而节省计算机内存并节省计算时间。

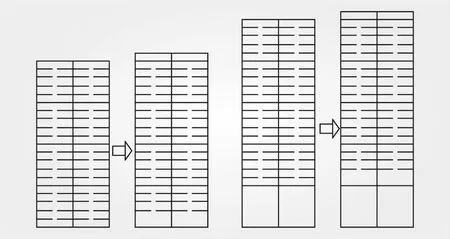
图3 单元浮动示意

浮动网格法最关键的技术是研究何时开始浮动能控制浮动与不浮动之误差在允许范围之内。因RCC的弹性模量、徐变度、水化热等特性随时间和不同标号混凝土而变化，因此，计算中控制何时开始浮动是控制计算误差非常重要的因素。

网格浮动后采用平均龄期的弹性模量、徐变度和水化热温升代替各小薄层相应的材料参数。

浮动网格法的雏形为“互层单元”，早在1989年三峡大坝混凝土的快速施工和分缝研究计算时被采用，将两层或多层合并为一个单元。经过发展后，浮动网格法逐步用于碾压混凝土坝的仿真计算[13，17-18]中，并取得了一定的成效。

浮动网格法采用比较巧妙的变单元坐标的方法降低了成层结构有限元分析规模大的问题，而且该方法对变单元时引起的误差控制比较严格，因此浮动过程中计算精度可以得到一定的保证。但是该方法在每次浮动变单元时存在一个新旧单元数据移植的问题，实施起来比较麻烦；而且对截面形式复杂的模型不大适用；对于横向相邻浇筑层，由于施工进度不一样，要用过渡单元连接，该方法没有考虑这方面的问题。

2.5 层合单元法

层合单元是上世纪末国内外刚发展起来的一种新型单元。对于以碾压混凝土坝为代表的成层结构，有限元分析的单元按照常规方法必须分得很小，这使得计算量十分巨大。层合单元一改常规有限元单元内的材料属性必须单一的规定，允许单元内存在多层材料(如图4所示)，甚至每层材料中可以分段，使有限单元法的应用得到了很大范围的推广。

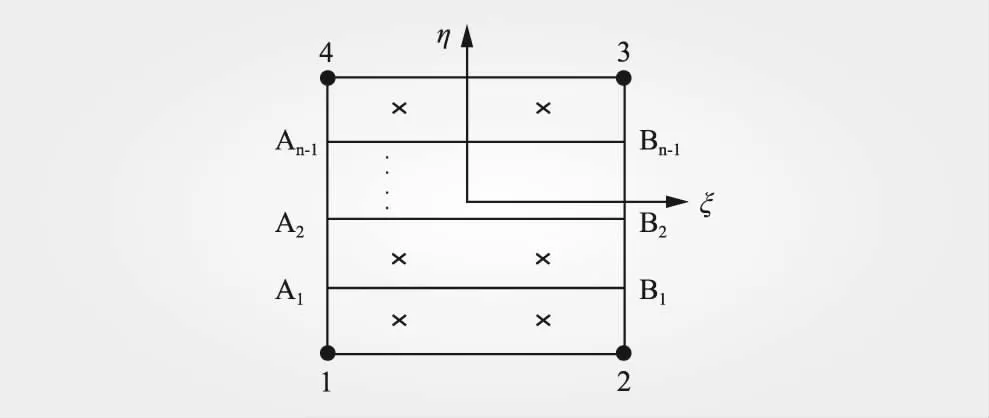
图4 层合单元示意

2.5.1 非均匀单元方法

1995年，王建江等[19]在前人[20-21]对碾压混凝土坝温度应力研究的基础上，提出了“非均匀单元方法”，建立非均匀模型以及等效均匀模型，以含有不同龄期RCC材料的大单元代替均匀材料小单元，从而可以提高温度应力计算效率，并应用于龙滩碾压混凝土重力坝的计算[22]。

如图5所示，层合单元内各层的材料特性成阶梯状分布。以绝热水化热温升为例，设均质碾压混凝土的绝热水化热温升可表述为

θ(t-τ)=θ0·(1-e-s(t-τ))

(2)

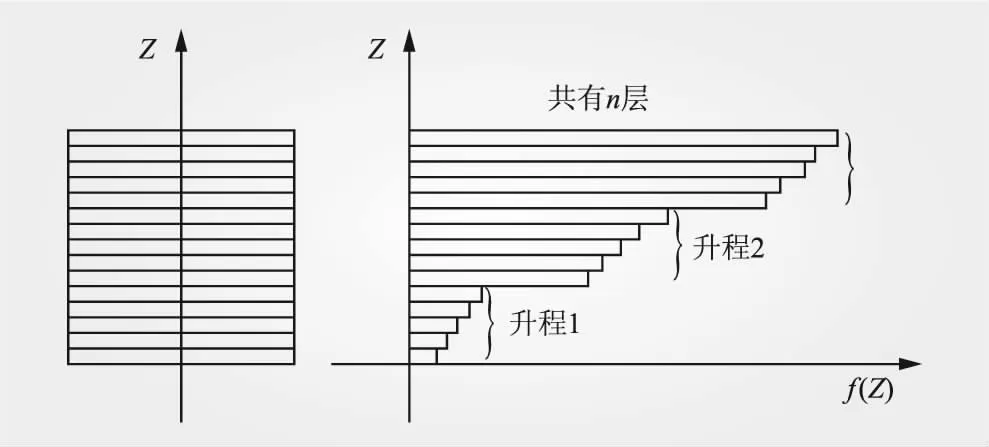
图5 层合单元内不同升程物理量分布差异

对于含有n层RCC的非均质单元，若碾压层i的龄期为τi，记层间隔为Δτ，则单元内的阶梯状分布的水化热绝热温升可表示为单元局部坐标V的函数，即

θ(t，V)=θ0·(1-e-s(B1-B2V))

(3)

式中，B1=t-(τ1+τn)/2，B2=(τn-τ1+Δτ)/2。

与水化热绝热温升类似，用连续函数描述非均匀体的弹性模量和徐变度，即

E(t，V)=E0(1-e-a(B1-B2V)b)

(4)

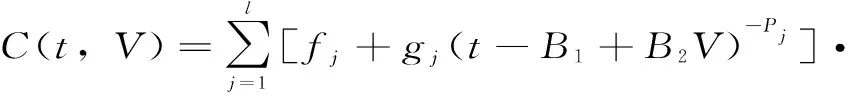
(5)

式中，l为徐变的级数，f、g、P、r为徐变度参数。

非均匀单元法通过式(3)把单元内的绝热温升近似为单元局部坐标的函数，实际上是把各层的差异人为抹匀，简化了有限元分析难度，提高了计算效率。由于相邻升程之间材料特性参数有较大的突变(如图5所示)，这样处理会引起一些误差。

2.5.2 虚拟层合单元

虚拟层合单元是在层合板壳的等效单层理论和分层理论的基础上产生的[23]。

有限元法广泛用于箱形桥梁的分析，研究采用的梁单元多种多样[24-26]，一般要划分较多单元数。1998年，凌道盛等[23]在一种16节点的相对位移板壳单元[27]的基础上，利用分层积分化“分”为“合”的思想，构造出“虚拟层合单元”。

虚拟层合单元在单元内部可以有许多层，每层中又有多种不同材料，在计算单元刚度矩阵、单元质量矩阵和应力时，由于各层或各段材料参数、几何参数不同，进行分层分段积分。以刚度矩阵为例，其积分方式为

(6)

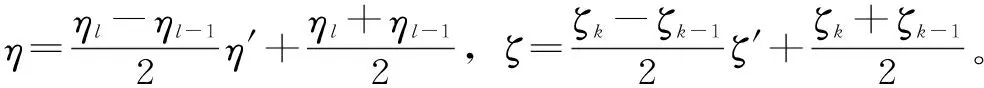
“虚拟层合单元法”通过坐标变换，对不同材料分层分段使用高斯积分。根据这种思路，还可构造不同的单元[28-29]以满足不同的工程需要。

“虚拟层合单元法”不仅可以在某一方向上分层，而且可以在层内分段，提高了单元应用的灵活性，不过这是建立在对每层每段材料高斯积分的基础上，其处理过程相当复杂。

2.5.3 非均质层合单元法

2004年，朱岳明在“非均匀单元方法”和“虚拟层合单元”的基础上，提出“非均质层合单元法”[9]。

非均质层合单元法只把同一升程内各层的材料特性参数采用连续函数描述，并用“虚拟层合单元”的分层分段积分方法，在数学上更严密。

该技术将RCC施工的每个升程简化为一个非均质层，整个层合单元网格包含若干这样的非均质升程层；对顶部的新浇混凝土，自动退化成薄层均质单元，计算网格随着坝体混凝土的浇筑而不断浮动上升与扩网，但对每一个薄层单元只扩网一次。

该单元法在新老混凝土过渡时只需要进行一次单元调整和扩网，形成常规单元尺寸的非均质层合单元。

“非均质层合单元法”综合了浮动网格法、“非均匀单元法”和“虚拟层合单元法”等多种方法的优缺点，相对比较成熟，不过仍然有如下问题：①形成层合单元存在一次并网的过程；②对每个升程的各碾压层，其材料参数用一个简单连续函数来描述。问题①使得计算过程仍然复杂，问题②将导致一些误差的产生。

2.5.4 层合单元修正算法

针对层合单元内各层材料力学性质相差较大和单元的变形特点(见图6)，彭文明[30]提出层合单元位移插值函数的修正算法。修正的单元形函数采用连续函数或分段函数，可以解决常规双线性插值函数在描述单元变形时无法考虑各层材料参数差异带来影响的问题，减小线性变形取代沿层厚方向的折线变形引起计算误差。修正形函数可以解决单元内不同材料由于力学性质相差较大引起的误差扩散问题，比常规层合单元的计算精度高。

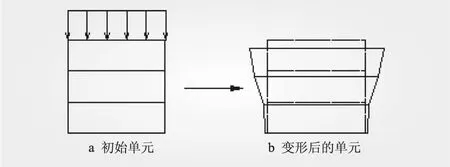
图6 层合单元位移示意

2.6 分区异步长算法

分区异步长算法可用于计算比较复杂的不稳定温度场[31-32]和弹性徐变体应力场[33]，本文主要介绍该算法在温度场分析中的应用。不稳定温度场的有限元求解方法，在空间域用有限单元离散，在时间域用差分法离散[34]。常规算法是对整个计算区域采用相同的时间步长，一般要根据温度变化速率大的新浇混凝土部分区域，统一用小步长计算。

使用分区异步长算法，在温度变化剧烈的区域，采用较小的时间步长，而在其余广大区域，采用较大的时间步长，从而可提高计算效率。

如图7所示，温度变化剧烈的区域为R1，过渡区域为R2，其余的温度变化平缓区域为R3。区域R2和R3中的绝热温升θ2和θ3假设已经趋于平稳，只有区域R1中的绝热温升θ1变化剧烈。θ1只影响R2的一部分，所以假设θ1对R3无影响。

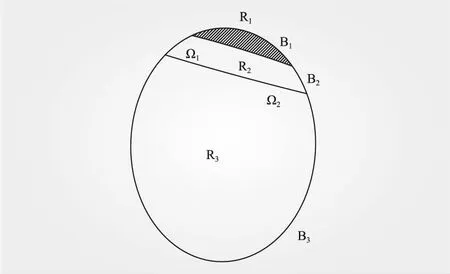
图7 分区异步长法示意

分区异步长法在计算域上为碾压混凝土坝的仿真模拟开拓了一种新的思想。不过该方法的实现是建立在一个假设的基础上的，即小步长区域(新浇混凝土)对大步长区域(老混凝土)无影响，该假设将使得计算结果存在一定误差。

3 混凝土浇筑的连接模拟技术

3.1 新老混凝土间接缝单元

接缝单元是为了配合并层算法而提出的。使用并层算法可有效的减少坝块的计算层数，计算量得到极大的简化。但是大体积混凝土常设许多纵横接缝，把混凝土结构分成许多柱状块体。如图8所示的A、B两个浇筑块，B块顶部处于浇筑过程，需要采用密集网格，如果采用常规有限元方法计算，A块与B块顶部相连的混凝土单元厚度也不能过大，这就限制了并层的效果。

朱伯芳[35]提出一种特殊的接缝单元，使得基岩与坝体以及坝内的各坝块均可各自单独并层，互不影响。

图8为不同施工高度的浇筑块，图8中A块与B块顶部相连的混凝土采用大的并层单元，B顶部采用小单元，大单元通过接缝单元与小单元连接，一个大单元与多个接缝单元相连，每个接缝单元与一个小单元对应。

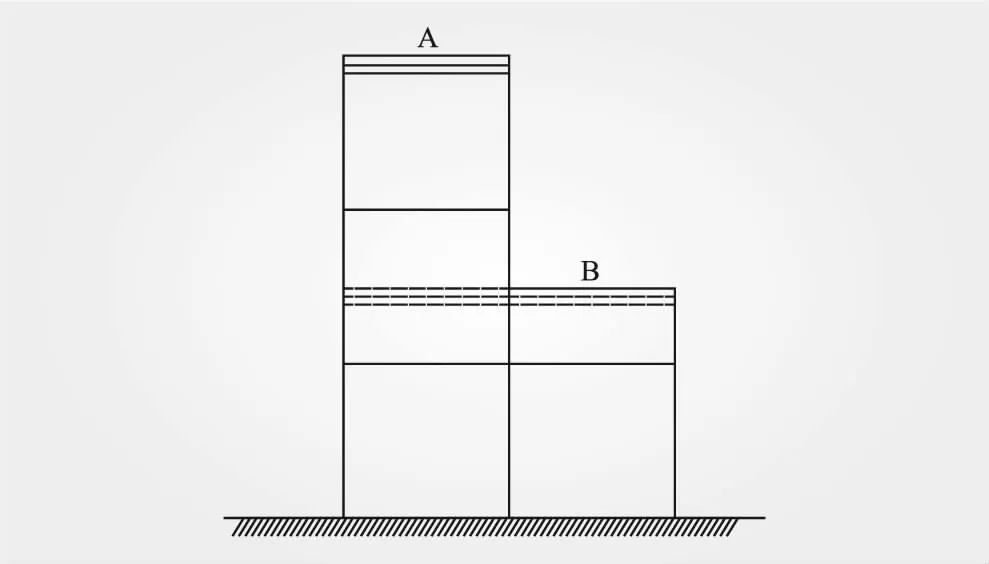
图8 不同施工高度的浇筑块

接缝单元方便了并层算法在不同进度的相邻浇筑块之间的使用。接缝单元必须取得足够薄，以便假设沿单元厚度方向应变为常量；并层算法对均质单元需要并网，并网过程中接缝单元应进行妥善处理。

3.2 生长连接模型

如图9所示，A、B仓面浇筑高程不同步，B仓面上部单元与已浇筑的A仓面需要连接。生长连接模型[36]由生长单元、层合单元和连接层合单元组合而成。其中生长单元随着碾压升程的抬高，逐渐“长大”，最终变成层合单元，如图9中的生长单元2 675最终变成层合单元267’3；因此，生长单元本质上是含有多层不同材料的层合单元，只不过它的层数随着混凝土浇筑施工会动态增加。在生长单元成长的过程中，界面处与之相连的老混凝土层合单元，需用连接层合单元过渡，如图9中的五节点单元12 534。

图9 生长连接模型模拟施工浇筑块

生长连接模型核心思想是用生长单元模拟新浇混凝土的碾压施工过程，同时用连接层合单元取代相应位置的层合单元，并与生长单元相连，使有限元网格单元之间没有“缝隙”。相比并层算法、浮动网格等技术，生长连接模型不需要对有限元整体网格进行并网，仅需要处理接缝连接部位的个别单元，大大简化了有限元网格重构的处理流程，更好保证计算效率和精度。

该模型可有效解决混凝土碾压施工薄层生长和新老混凝土连接问题，计算过程需控制连接层合单元与相应位置层合单元的激活与冻结。当然，连接层合单元为五节点等参单元，与四节点生长单元相连接部位存在局部不协调问题，根据圣维南原理[10]，不协调的影响对有限元计算可忽略不计。

生长连接模型还可以用于岸坡岩基上混凝土浇筑过程的模拟，如图10所示。图10中，混凝土逐层浇筑，在岸边基岩接触部位设置连接单元，就可以实现混凝土薄层浇筑细网格与岩基粗网格的过渡，同时，混凝土逐层浇筑通过生长单元模拟，大大减少计算网格的数量。

图10 生长连接模型模拟岩基上混凝土施工(单位： cm)

3.3 材料非线性接缝模型

在新老混凝土、混凝土与岩体的交界面，由于温度变化和渗水等作用，交界面无法承受法向拉应力，但闭合时可传递压力以及剪力，这些接触界面对结构安全有很重大的影响。段云岭等[37]提出材料非线性的接缝数值模型，该模型可以模拟混凝土结构工程交界面不考虑法向粘结作用。

4 水管冷却效果的模拟技术

冷却水管是大体积混凝土施工重要的温控措施。冷却水管施工仿真计算，具有较大的难度。朱伯芳院士提出的等效算法[38]，将水管冷却效果等效为负热源进行计算，这是一种简化而易操作的方法。等效算法计算效率很高，在大规模温控计算中被广泛采用。

冷却水管尺寸小，在混凝土温度场精细数值模拟仿真中，专家们也取得了一些成果。刘宁等[39]将水管冷却周围的一组单元凝聚为一个单元，研发了水管冷却的有限元子结构的模拟技术，有效缩小了计算规模，也提高了计算效率；苏培芳等[40]采用复合单元法离散模拟冷却水管，避免了冷却水管绘制网格的困难；刘杏红等[41]、张超等[42]开发的热一流耦合精细算法程序，对大体积混凝土采用水管冷却的温度场及应力场可进行精细的数值仿真分析，程序可适应冷却水管不同的布置形式(见图11)，计算结果可正确反映冷却水管周围的温度梯度。

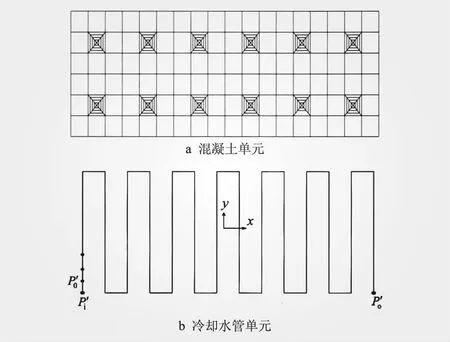
图11 混凝土与冷却水管单元划分

5 展 望

学者们对薄层碾压施工仿真进行了很多研究，结合已有成就和RCC结构施工期温度应力仿真的重难点，对今后的研究方向提出如下展望。

(1)需进一步研究水管冷却效果模拟技术。水管冷却是混凝土温度控制的重要措施之一。冷却水管的真实模拟中，涉及热学、流体力学和固体力学问题，冷却水温度随时间、空间一直变化，给数值计算提出了较大挑战。另一方面，由于冷却水管的半径只有1～2 cm，水管冷却在有限元计算模拟的网格要求非常密集，大大增加计算效率，甚至无法进行计算。

(2)需加强研究接触界面的热学和力学问题。新老混凝土及混凝土与岩石浇筑的接触面，对结构温度传递、变形协调起着至关重要的作用。接触面是网格划分的连接纽带，同时接触面的热学和力学性能复杂。目前数值模拟对接触面的研究还有所欠缺，值得进一步深入研究。