带变量核的高阶交换子在加权Morrey-Herz空间上的有界性

邵旭馗， 王素萍

陇东学院 数学与统计学院， 甘肃 庆阳 745000

记Sn-1为Rn(n≥2)中的单位球面， 其上的Lebesgue测度用dσ=dσ(x′)表示． 定义在Rn×Rn上的函数Ω(x，z)∈L∞(Rn)×Lr(Sn-1)(r≥1)， 满足

(1)

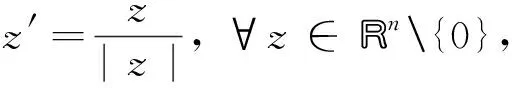
(2)

并设

Ω(x，λz)=Ω(x，z) ∀x，z∈Rn， ∀λ>0

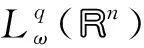
(3)

设b∈BMO(Rn)， 对m∈Z+， 带变量核的高阶交换子定义为

(4)

其中

B(x，r)={y∈Rn： |x-y|≤r}

文献[1]证明了带粗糙核的高阶交换子Mb，m，Ω当m=1时(简记为Mb，Ω) 在齐次Herz空间上的有界性． 文献[2]得到了Mb，m，Ω在齐次Morrey-Herz空间上的有界性． 随后， 文献[3]又证明了当b∈BMO(Rn)，m∈Z+时，Mb，Ω是齐次Morrey-Herz空间上的有界算子． 文献[4]利用Sharp极大函数， 证明了带变量核的Marcinkiewicz积分算子μΩ和某一类加权Lipschitz空间的函数b生成的交换子的加权有界性． 最近， 文献[5]得到了变量核Marcinkiewicz积分与BMO函数生成的交换子在变指标Herz-Hardy空间上的有界性． 有关变量核积分算子及其交换子的相关结果详见文献[6-13]．

受以上研究的启发， 一个自然的问题就是： 带变量核的高阶交换子Mb，m，Ω在齐次Morrey-Herz空间上是否也有界? 本文考虑了这一问题， 并证明了带变量核的高阶交换子Mb，m，Ω在加权齐次Morrey-Herz空间上的有界性， 推广了以往非变量核的结果．

首先给出一些定义与记号：

设k∈Z， 记

Bk=B(0， 2k)={x∈Rn： |x|≤2k}

及Ck=BkBk-1， 并记χk=χCk为集Ck的特征函数．

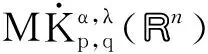
其中

定理1对某个r∈(0， ∞]， 设Ω∈L∞(Rn)×Lr(Sn-1)是0阶齐次函数且满足(2)式， 设b∈BMO(Rn)， 带变量核的高阶交换子Mb，m，Ω由(4) 式所定义． 如果p∈(0， ∞]，q∈(1， ∞)，ω1∈Am1，ω2∈A1和λ>0， 若α，λ，r和q满足以下条件之一：

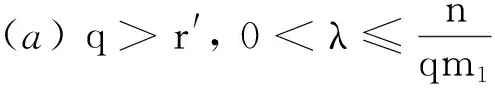
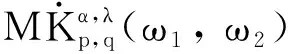
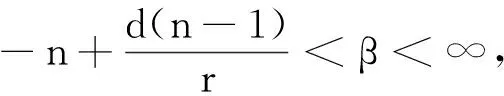
引理2[16]如果ω∈Ap(1≤p<∞)， 则存在常数C>0和δω(0<δω<1)， 使得： 当kj时，ω(Bk)/ω(Bj)≤C2(k-j)np．

定理1的证明首先证明在条件(a)下， 结论成立．

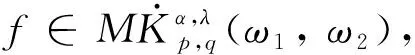
设

则

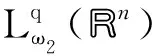
关于F1， 注意到x∈Ck，y∈Cj，j≤k-2， 因此|x-y|～|x|， 且ω2∈A1． 于是由假设

再根据引理1以及文献 [3] 中定理1的证明方法， 有

可选择适当的β， 使得

所以， 根据引理2， 有

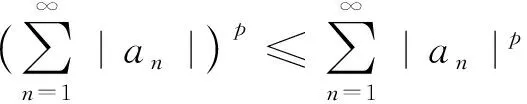
当1

最后来估计F3． 注意到， 当x∈Ck，y∈Cj，j≥k+2时， 有|x-y|～|y|， 类似于F1的估计方法， 我们有

于是

当0

当1

类似地可证在条件(b)下结论也成立， 至此， 定理1得证．