求解二维热传导方程的一个高精度显格式

詹涌强

广东交通职业技术学院 基础部数学教研室， 广州 510800

抛物型方程是偏微分方程中的一种重要方程， 它广泛应用于力学、 天文学、 物理学、 生态学及工程技术等各个领域中， 对于上述各领域中的许多问题， 为了定量或定性地对它们展开系统的研究， 需要建立各种数学模型， 而建立起来的这些数学模型最后都可归结为求解相应的抛物型方程， 这些抛物型方程是没有精确解的， 我们只能通过计算机求它们的数值解， 常见的数值解法有有限元法、 有限体积法、 边界元法和有限差分法等． 这些方法中， 有限差分法仍然是求解抛物型方程的重要方法． 经典的差分格式， 有古典显式格式、 古典隐式格式、 Crank-Nicolson格式等， 这些差分格式形式简单且稳定性条件好， 但它们的截断误差(精度)低， 古典显式格式与古典隐式格式的精度仅为O(Δt+Δx2)， Crank-Nicolson格式的精度为O(Δt2+Δx2)[1-2]， 与精确解的误差都较大． 因此， 高精度且稳定性好的抛物型方程的差分格式的构造成了许多学者研究的问题．

生态学中提出的各种数学模型、 神经轴突中电脉冲的传导及燃烧理论等许多物理现象， 以及热的传导、 流体在多孔介质中的运动规律等可归结为如下经典的抛物型方程-热传导方程， 本文讨论二维的情形：

(1)

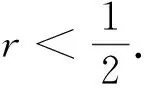
1 一个差分近似式

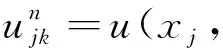
化简得

为方便起见， 记

2 高精度差分格式的构造

利用上面的差分近似式和已知的差分近似式构造如下的差分格式来逼近方程(1)

(2)

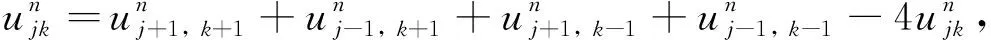
将(2)式中各节点上的u在节点(jΔx，kΔy，nΔt)处作Taylor展开， 整理可得

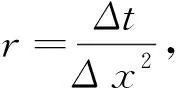
(3)

解方程组(3)可得

将各参数的值代回(2)式中， 即得到一个截断误差为O(Δt3+Δx4)的三层显式差分格式

(4)

3 差分格式的稳定性分析

下面利用Fourier分析法分析格式(4)的稳定性， 首先写出与格式(4)等价的两层格式组

(5)

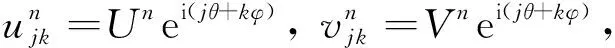
其中：

g21=1g22=0

传播矩阵G(s1，s2)的特征方程为

λ2-g11λ-g12=0

(6)

引理1[13]特征方程(6)的根满足|λ1，2|≤1的充要条件是

|g11|≤1-g12≤2

(7)

引理2[13]差分格式(4)稳定， 即矩阵族Gn(s1，s2)(0≤s1，s2≤2，n=1，2，…)一致有界的充要条件是

1) |λ1，2|≤1(λ1，2是方程(6)的两个根)．

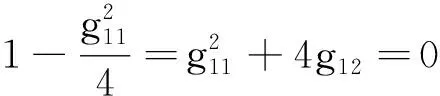
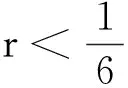
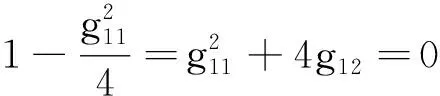
先讨论g11≤1-g12， 可得

(8)

为确定起见， 不妨假定

1-12r2>0

该式成立的条件是

(9)

当(9)式成立时， (8)式可化简为

8r2(6r-1)(s2+4s1)≤0

该式成立的条件为

(10)

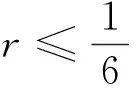
-3(6r-1)+4r2s2+16r2s1>0

(11)

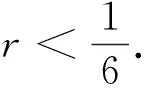
最后由-1+g12≤g11可得

24r2-6r+1+2r2(2r-1)(s2+4s1)≥0

(12)

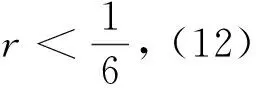
24r2-6r+1+20r2(2r-1)≥0

也即

40r3+4r2-6r+1≥0

(13)

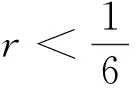
综上所述， 由Lax的稳定性与收敛性定理， 定理1得证．

4 数值算例

在本节中， 通过两个数值算例， 利用MATLAB软件进行数值模拟， 将本文提出的格式(4)与文献[11]和文献[12]格式进行比较， 进一步证明本文提出的格式是一种高精度的差分格式．

例1考虑如下带有初边值问题的二维热传导方程

(14)

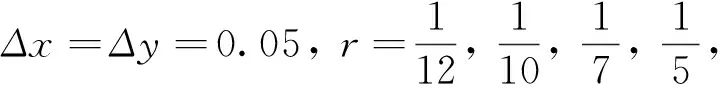
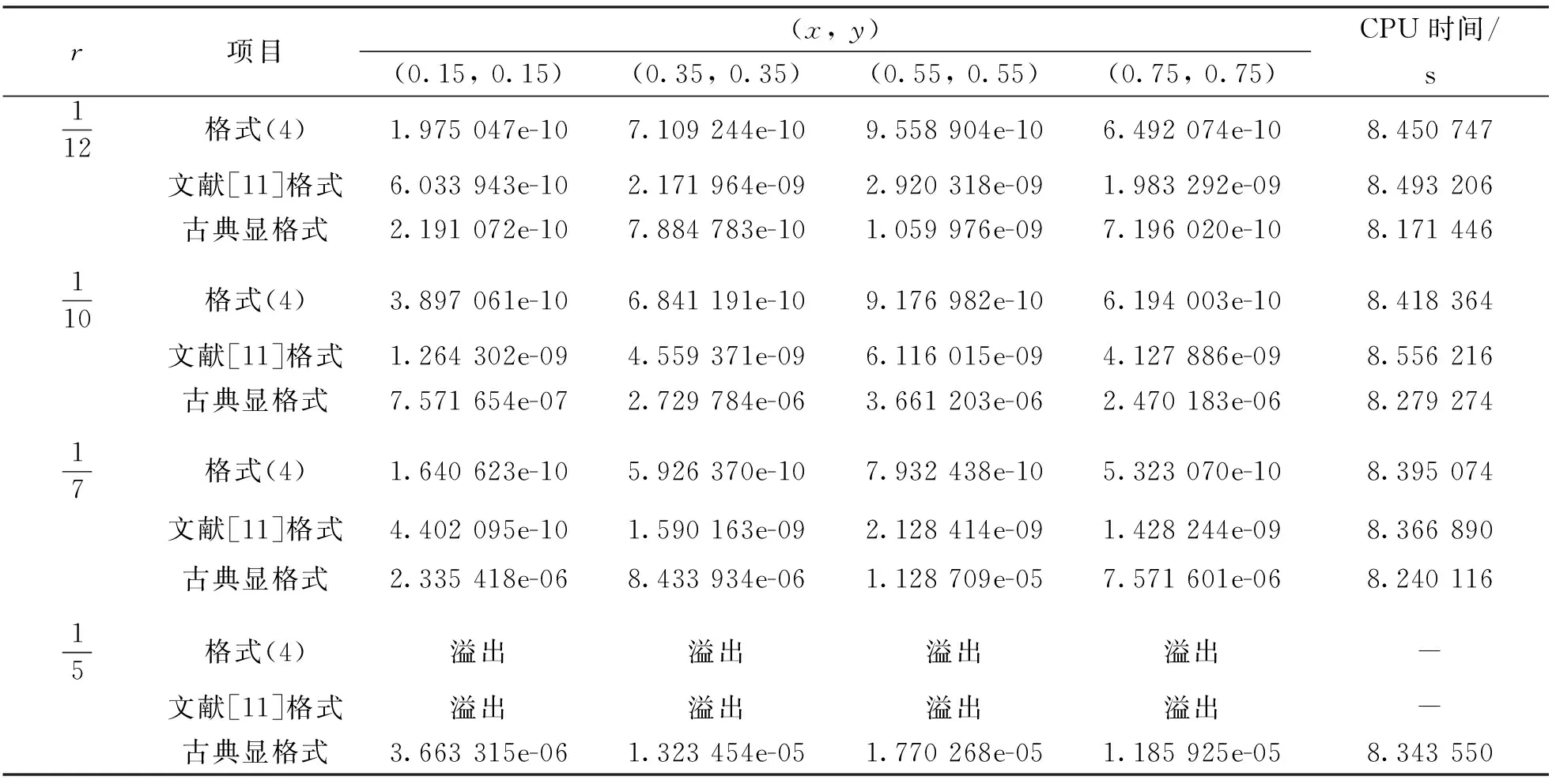
表1 在Δx=Δy=0.05， n=800时3种格式数值解与精确值的误差绝对值和计算效率的比较

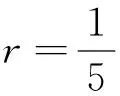
例2

(15)

表2 算例2中本文格式与文献[12]格式和精确解之间的比较

从以上两个数值算例可以看出， 本文格式的收敛性及稳定性与理论分析一致， 说明本文格式是一种有效的差分格式．