基于ANSYS/LS-DYNA的果枝修剪过程仿真与试验研究
孙健峰,邢凯峰,杨 洲,2,段洁利
(1 华南农业大学 工程学院, 广东 广州 510642; 2 嘉应学院/广东省山区特色农业资源保护与精准利用重点实验室, 广东 梅州 514000)
中国是水果种植和生产世界第一大国,2019年果园种植面积为1.23×107hm2,水果产量达2.74×108t[1]。果树修剪是果园管理过程中的重要环节,是决定果树能否健康生长的重要因素,直接影响果实产量及品质[2-3]。目前我国果园生产综合机械率不足30%,果树修剪机械较少,修剪作业以人工修剪为主,修剪效率低,劳动强度大,且易造成主枝断裂,降低水果生产效益[4-5]。欧美等发达国家普遍使用标准化果园机械进行修剪作业,机械化程度高[6-7]。我国南方果园多为丘陵山地,地貌特性严重限制微型修剪机械作业,同时龙眼、荔枝等主要果树树枝硬度和纤维剪切强度高于一般林果类树枝,部分果园开始使用便捷高效、剪切强度高的电动修剪机作业[8-10]。尽管电动修剪机优势较多,但成本高、刀具易损坏,严重制约电动修剪机的普及,不利于果园机械化的发展与推广[11-12]。为解决上述问题,已有学者针对电动修剪机刀具耐磨性能展开研究[13-14],但鲜有分析电动修剪机修剪树枝过程特性,因此研究树枝修剪过程特性及切割机理对提高电动修剪机切割性能具有现实意义。
近年来,诸多学者对树枝和农作物茎秆的切割过程进行相关研究。王芳等[15]采用摆切式切割试验台对向日葵花茎秆切割能耗进行试验,研究切割速度、滑切角、割刀刃角对切割能耗的影响,结果表明3个影响因素对切割能耗影响的顺序为:切割速度>滑切角>割刀刃角;王慰祖等[16]通过理论力学和弹性地基梁理论对直刃刀片切割树枝过程进行理论建模,利用此模型可对刀片切割力作出准确预测;康峰等[17]通过自制苹果树枝切割试验平台,探究刀具滑切角、平均切割速度和切割间隙对峰值切割力的影响,获得最优切割参数组合为:刀具滑切角20°、平均切割速度0.4 m/s、切割间隙1.5 mm;张燕青等[18]通过茎秆往复式切割试验台对谷子茎秆进行单因素切割试验,最终得到最优切割参数为:平均切割速度1.19 m/s、切割倾角7.2°、刀片斜角36.4°;Vu等[19]利用自制切割试验平台,以玉米秸秆作为试验对象,评价了切割速度、切割角和进给角对切割力和功耗的影响;Mathanker等[20]研究刀片倾角及平均切割速度对甘蔗切割功耗的影响,结果表明切割功耗随平均切割速度的增大而增大,当平均切割速度为7.9 m/s、刀片倾角为60°时,切割功耗最小。
上述研究大多致力于刀具切力、切割功耗、切割运动参数和刀具组合优化等方面,主要通过参数优化进行研究,对切割机理的研究相对偏少,针对南方果园高硬红木树枝切割过程的仿真研究更少,研究高硬红木树枝切割过程对实现南方果园修剪机械化,提升龙眼、荔枝的市场竞争力具有重要意义。此外,与理论试验研究相比,有限元仿真可以缩短试验周期,动态分析树枝切割过程及切割机理。本文根据电动修剪机修剪树枝的特征,以龙眼‘石硖’品种树枝为研究对象,对树枝切割过程建立有限元模型,并通过试验验证模型的准确性,使用高速摄像机观察树枝切割过程,分析动刀片、树枝、定刀在切割过程中的应力分布、修剪过程特性及切割机理,为今后修剪机具切割部位的设计和改进提供一种解决途径。
1 仿真模型与试验设计
树枝修剪过程复杂多变,刀具与树枝之间属非连续、非线性、动态大变形接触,常规方法难以分析刀具与树枝之间的相互作用过程。本文根据电动修剪机修剪树枝的特性,通过有限元仿真软件ANSYS/LS-DYNA建立树枝切割过程仿真模型,全面阐述模型的建立过程及相关细节。
1.1 仿真模型的建立
1.1.1 几何模型 电动修剪机是以蓄电池为动力源的手持式机械化修剪机具,修剪树枝过程是刀具与树枝之间不断相互作用的复杂过程,修剪树枝主要由动刀实现,定刀则起支撑树枝和辅助修剪的作用,动刀在外载荷的作用下向下运动并最终剪断树枝。图1为电动修剪机结构示意图。

图1 电动修剪机结构示意图Fig. 1 Schematic diagram of electric pruning machine
为提高仿真的准确性并缩短计算时间,在三维建模软件SolidWorks中以1∶1的比例对电动修剪机切割部位进行建模。为方便仿真计算,将动刀分为刀柄和动刀片,同时将刀柄设置为转动体[21],忽略模型中倒角、倒圆等结构,并转换为IGES文件格式导入到ANSYS/LS-DYNA软件中。几何模型中动刀厚度为6 mm,刀刃倾角为20°,定刀厚度为6.5 mm,树枝长度为120 mm。几何模型如图2所示。
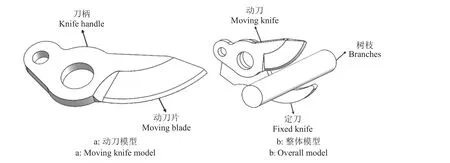
图2 电动修剪机切割部位几何模型Fig. 2 Geometric model of the cutter part of electric pruning machine
1.1.2 确定材料类型和材料本构 动刀片、定刀、树枝均采用3D Solid 164实体单元,刀柄采用3D Shell 163薄壳单元。将动刀片和定刀定义为弹性体,采用线弹性各向同性弹性材料模型(*MAT_ELASTIC),为缩短仿真计算时间,刀柄采用刚性体材料模型(*MAT_RIGID),将动刀片和刀柄通过布尔运算连接起来,使动刀片在刀柄的带动下进行转动,刀具材料模型参数按照SK-5的参数进行设置。选用龙眼‘石硖’品种树枝作为切割对象,龙眼树枝主要由树皮和树芯组成,近似为圆柱实体,具有非匀质、非线性、正交各向异性等特性,材料性能符合弹性力学的基本要求。龙眼树枝模型选用线弹性正交各向异性材料模型(*MAT_ORTHOTROPIC_ELASTIC),该模型主要由质量密度和9个独立弹性常数组成,这9个独立弹性常数包括3个弹性模型 (EX、EY、EZ)、3 个泊松比 (μXY、μXZ、μYZ)和 3 个剪切模量(GXY、GXZ、GYZ),由文献[21-23]确定龙眼树枝材料本构。刀具和龙眼树枝材料本构:1) 刀具,SK-5,密度 7 900 kg·m-3,弹性模量 2.10×105MPa,泊松比 0.275,屈服极限 930 MPa ;2) 龙眼,密度 951.5 kg·m-3,EX为 216.3 MPa,EY为547.2 MPa,EZ为 52.1 MPa,μXY为 0.43,μXZ为0.03,μYZ为 0.015,GXY为 56.3 MPa,GXZ为22.4 MPa,GYZ为 11.0 MPa。
1.1.3 网格划分 本文对动刀片和树枝接触部位的网格进行细化,对刀柄网格尺寸粗化。有限元模型网格划分如图3所示,整个模型共创建4个部分, PART1为动刀片模型,PART2为定刀模型,PART3为树枝模型,PART4刀柄模型。

图3 有限元模型网格划分Fig. 3 Meshing of finite element model
1.1.4 定义接触算法和边界条件载荷 实际切割中动刀片会将树枝剪断,故在设置接触时,动刀片与树枝间选择面面侵蚀接触,其中动刀片和树枝分别设定为主接触体(MSID)和从接触体(SSID),设定静摩擦系数为0.14,动摩擦系数为0.26[22,24]。定刀与树枝在实际中发生侵蚀的接触面积较少,故选择自动面面接触。
在有限元模型中,对树枝模型(PART3)一端的表面和定刀模型(PART2)孔内壁表面施加全部自由度约束,对刀柄模型保留绕Z轴的转动自由度,其余自由度全部约束。设置刀柄模型(PART4)绕Z轴的转速为2.5 rad/s。
1.2 仿真试验设计
分别对直径为10、15和20 mm的树枝进行切割仿真,仿真时间分别为0.4、0.5和0.6 s。通过后处理模块LS-PREPOST观察整个模型的切割过程,提取相关结果信息,分析切割力数据及各部位模型随时间变化的应力分布情况,并输出相应曲线。
2 验证试验与结果分析
为验证仿真模型的准确性,本文通过搭建树枝切割试验平台分别对直径为10、15和20 mm的树枝进行切割试验,使用高速摄像机观察树枝切割过程,记录切割力数据,绘制相应的曲线图,与仿真模型结果进行对比分析。
2.1 试验材料
本试验将‘石硖’品种龙眼树枝作为切割对象,采样地点为广东省农业科学院果树研究所龙眼果园,采集的枝条尽量通直,直径变化连续均匀,无病虫害,节数少,采样后剪去分枝装入帆布袋密封保存。
本试验选用 SK-5碳素工具钢刀片作为电动修剪机刀具,执行标准为JIS G4401-2009[25],其硬度:退火≤187 HB,压痕直径≥4.40 mm,淬火≥62 HRC。刀片主要参数尺寸为:90 mm×30 mm,刀刃倾角 20°。
2.2 试验设备与试验方法
图4为数据测试系统逻辑图,图5为本文搭建的树枝切割试验平台。本试验采用电动修剪机作为切割部件,通过高速摄像机观察修剪过程特性,刀具在切割树枝时发生轻微形变,黏贴在动刀表面上的应变片也随之形变,从而产生电阻的变化改变电位,动态应变仪将捕捉变化电位进行数据采样,数据采集卡将其处理并转换为切割力值,通过USB接口线传输到计算机,最终获得切割力数据。试验时,使用电动修剪机分别对直径为10、15和20 mm的树枝进行切割试验,每组试验重复3次,记录切割力数据,绘制相应的曲线图。图5b为自制电动修剪机切割平台,该平台树枝导向管可将待切割树枝压紧,导向作用好,固定锁紧环可把电动修剪机稳定固定在机架尾端,使待切割树枝进入电动修剪机的切割工位。图5c为应变片接法示意图,由文献[26]可知测试电桥采用半桥接法,接入2个相同阻值应变片。其中一个应变片黏贴在动刀前刀面刀柄上,黏贴位置需满足:1)远离动刀作业区域,避免剪枝过程中应变片与树枝接触出现失效的情况,2)应变片所测数据免受刀具变形的影响;另一个应变片作为标记值贴到未工作动刀上的相同位置,应变片具体黏贴位置如图5d所示。
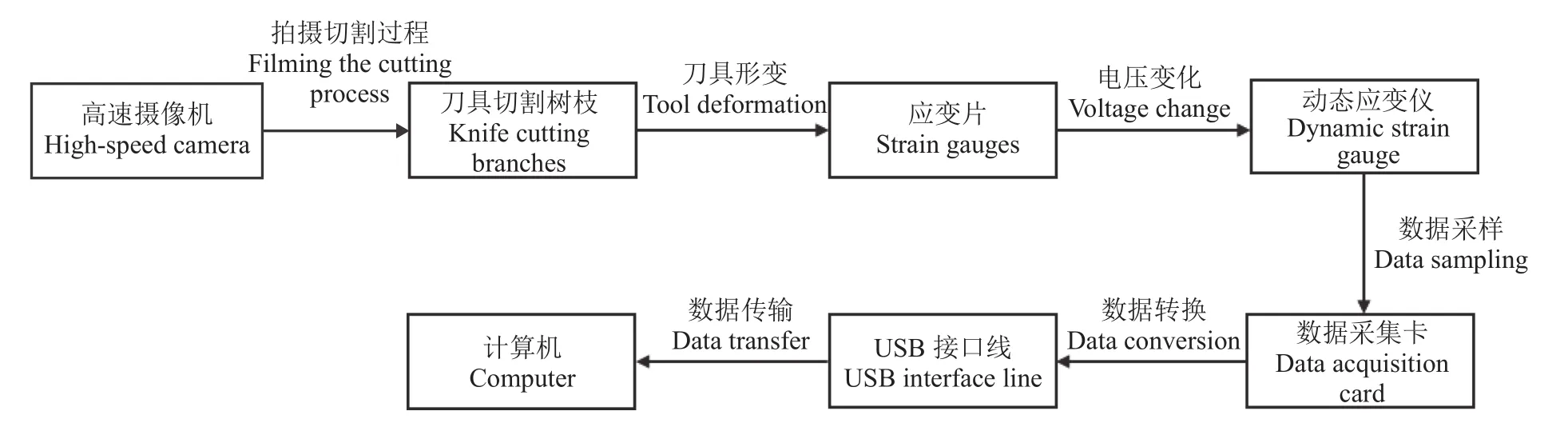
图4 数据测试系统逻辑图Fig. 4 Logic diagram of data test system

图5 切割试验平台Fig. 5 Cutting test platform
图6为自行搭建的应变片标定平台,为得到准确的剪切力数据,需要通过应变片标定试验确定桥路输出电压与压力的关系。

图6 应变片标定平台Fig. 6 Strain gauge calibration platform
图7为应变片标定逻辑图,通过手动转动试验台的摇杆,使连接在试验台上的螺栓和称重传感器向下运动,螺栓对刀具黏贴好的应变片施加压力,应变片产生形变,称重传感器接受压力信号,并传输至智能数字称重变送器进行处理,数据采集卡将其转换为压力值;同时应变片由于电阻值的变化而改变电位,动态应变仪将捕捉到的变化电位进行数据采样,数据采集卡将其处理并转换为电压值,两者通过USB接口线将数据传输到计算机,最终获得压力和电压数据。
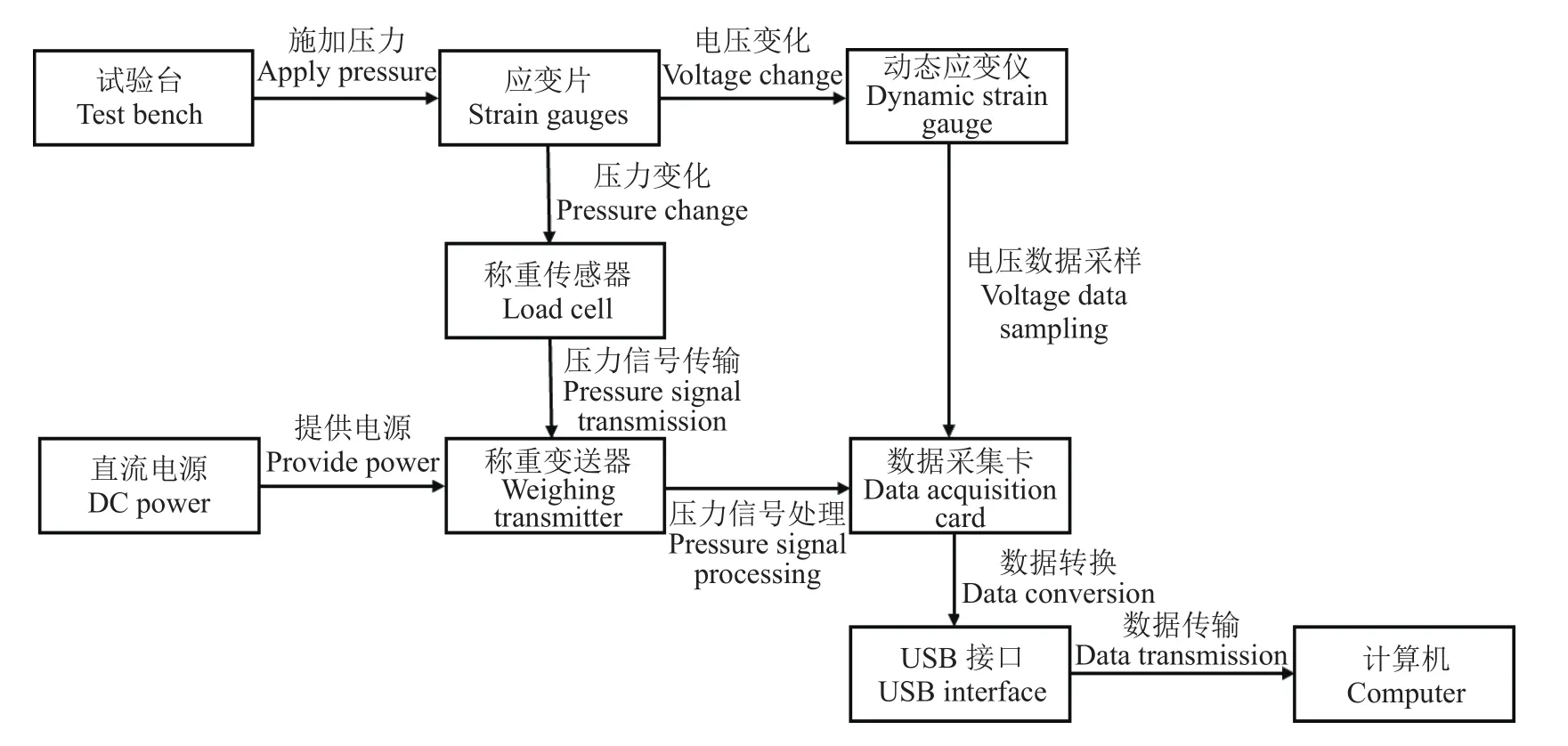
图7 应变片标定逻辑图Fig. 7 Logic diagram of strain gauge calibration
图8为应变片标定试验结果,FlexLogger软件可以直接换算压力值和电压值,故不必将电压值转换成应变值。用FlexLogger软件设置对应参数,斜率为0.58 kN/V,偏移为-0.009 kN。
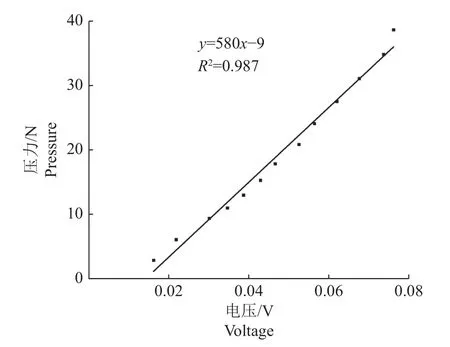
图8 应变片标定试验结果Fig. 8 Strain gauge calibration test result
2.3 试验结果与仿真结果对比分析
2.3.1 切割过程对比分析 本文以切割20 mm直径树枝为例,将高速摄像机拍摄的试验切割过程(图9)与仿真切割过程(图10)结合分析,可知试验切割过程与仿真切割过程都可分为5个阶段:挤压阶段、切入剪切阶段、稳定剪切阶段、剪断阶段、树枝振动阶段。

图9 20 mm直径树枝的试验切割过程Fig. 9 Test cutting process of 20 mm diameter branches
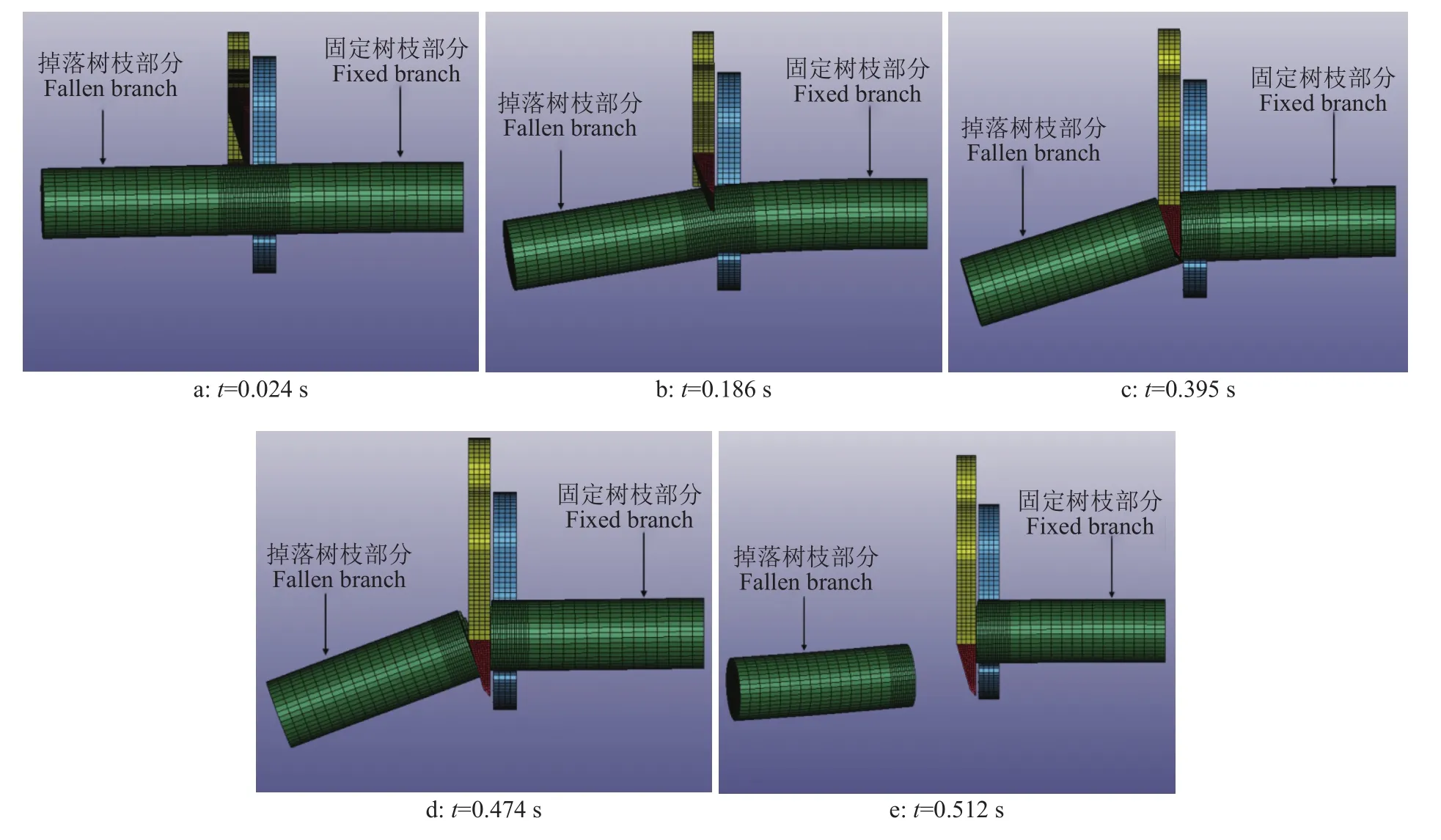
图10 20 mm直径树枝的仿真切割过程Fig. 10 Simulation cutting process of 20 mm diameter branches
在挤压阶段(图9a、10a)中,动刀片开始接触树枝,动刀片刀刃部分和定刀对树枝进行挤压,树枝发生弹塑性变形。
在切入剪切阶段(图9b、10b)中,动刀片开始切入树枝,树枝出现切口,受到刀具的挤压作用增强,动刀片本身的厚度会挤开两侧的树枝,掉落树枝部分在切口处产生弯折变形。
在稳定剪切阶段(图9c、10c)中,动刀片平稳切入,树枝切口扩大,倾斜程度增加,动刀片对树枝的挤压和摩擦作用减弱,树枝切口处弯折变形增强,树枝即将断裂。
在剪断阶段(图9d、10d)中,树枝从残留小部分断口到完全断裂。
在树枝振动阶段(图9e、10e)中,树枝已经断裂,但动刀片还未完全穿过树枝截面,树枝固定一端仍与动刀片后刀面作用,引起树枝振动。
2.3.2 切割力对比分析 图11为20 mm直径树枝切割力的试验曲线与仿真曲线,现以试验曲线为例分析,切割过程中刀具受力总体先增加后减少,当切割力达到最大值后开始下降,达到低点后小幅度波动直至为0。
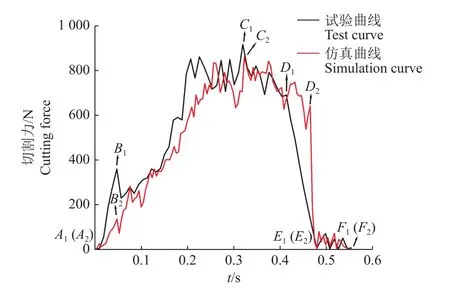
图11 20 mm直径树枝切割力的试验曲线与仿真曲线Fig. 11 Test and simulation curves of cutting force for 20 mm diameter branches
A1B1曲线段为挤压阶段,当动刀片开始接触树枝时,会将树枝推向定刀,动刀片刀刃部分和定刀对树枝进行挤压,树枝发生弹塑性变形,切割力不断增大。
B1C1、C1D1曲线段统称为剪切阶段,刀具受力总体先增加后减少,当切割力达到最大值后开始下降,且过程中伴有切割力的突升突降,这是由于此阶段不是纯剪切状态,树枝还会受到挤压、弯折等变形。
B1C1曲线段为切入剪切阶段,动刀片开始切入树枝,树枝不仅受到动刀片刀刃部分和定刀的挤压,还受到动刀片前后刀面的挤压,挤压作用增强,当树枝所受作用力超过其弹塑性变形后开始发生垂直树枝方向的剪切,由于刀刃存在厚度会挤开两侧的树枝,切割过程中掉落树枝部分对切口处产生弯矩,发生弯折变形,同时由于弯矩的存在,树枝出现微小裂纹并不断向内部扩展延伸,树枝断裂过程是剪切、弯曲和裂纹扩展交替进行。
C1D1曲线段为稳定剪切阶段,随着动刀片的稳定切入,树枝切口扩大,树枝倾斜程度增加,动刀片前刀面对树枝的挤压作用减弱,同时在掉落树枝部分重力的作用下,树枝切口处弯折变形增强,弯矩增加,裂纹扩展加速,故刀具受力在达到最大值后减小。
D1E1曲线段为剪断阶段,此阶段从树枝残留小部分断口D1点到树枝完全断裂E1点,掉落树枝部分在重力和动刀片作用下与刀具迅速脱离,切割力迅速下降,在树枝完全断裂处动刀片与掉落树枝不再发生作用,切割力达到此阶段最低点。
E1F1曲线段为树枝振动阶段,树枝已经断裂,但动刀片还未完全穿过树枝截面,树枝固定一端仍与刀具接触,树枝掉落的瞬间由于冲击的影响,引起固定端树枝的振动,对动刀片后刀面产生水平方向的冲击,故切割力在达到上一阶段最低点后小幅度波动直至为0。
由图11可知,仿真曲线与试验曲线趋势大致相同,但仿真曲线剪断阶段D2E2曲线段切割力下降速率更快,这是由于仿真时树枝被设定为圆柱弹性体,材料均匀,掉落部分树枝能够迅速脱离,而实际试验中树枝在断裂时由于表皮的存在,掉落部分树枝脱离速度减缓。
将实际试验数据与仿真数据进行比较,从表1对比可知,当树枝直径为10、15和20 mm时,刀具实际峰值切割力比仿真峰值切割力分别增加18.9、38.8和61.0 N,相对误差分别为7.8%、6.5%和6.6%。实际试验与仿真试验的刀具峰值切割力最大相对误差为7.8%,平均相对误差为7.0%,表明本文所建立的树枝切割过程仿真模型与实际情况基本符合,具有一定的参考价值。实际峰值切割力比仿真峰值切割力略大,且趋势大致相同,实际峰值切割力和仿真峰值切割力产生误差的原因有:1)仿真时设定树枝材料均匀,而实际树枝材料包括表皮、韧皮部和髓等部分,组成复杂;2)与仿真模型相比,实际试验切割过程树枝受挤压—剪切—弯曲多种受力形式,受力更加复杂;3)仿真模型中动、静摩擦因数等参数的设置与实际参数可能存在误差。

表1 实际试验与仿真试验的峰值切割力Table 1 Peak cutting force of actual test and simulation test
3 仿真应力分析
本文通过LS-PREPOST后处理模块动态观察树枝切割过程,分析动刀片、树枝、定刀在切割过程中的应力分布、修剪过程特性及切割机理,确定最大等效应力出现的区域。
3.1 动刀片应力分析
图12为20 mm直径树枝动刀片等效应力-时间曲线,图13为20 mm直径树枝不同时刻动刀片等效应力分布。由图12、13可知:切割过程中动刀片等效应力总体先增加,在达到最大值后降低,随后出现波动,在树枝断裂时等效应力迅速下降达到最低点,然后出现近似直线的波动。动刀片最大等效应力出现在刀刃附近,应力值为132.86 MPa,远小于刀具材料SK-5的屈服极限应力930 MPa,说明动刀片在切割树枝时不会发生失效。此外10和15 mm直径树枝动刀片最大等效应力分别为84.35和104.26 MPa,不会发生失效。
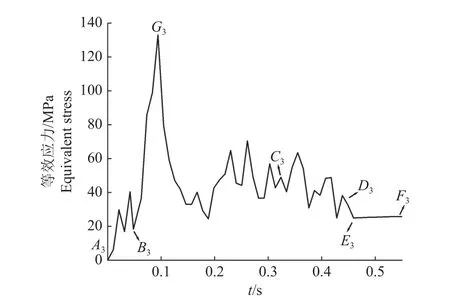
图12 20 mm直径树枝的动刀片等效应力-时间曲线Fig. 12 Equivalent stress-time curve of moving blade for 20 mm diameter branches

图13 切割20 mm直径树枝不同时刻动刀片等效应力分布Fig. 13 Equivalent stress distribution on moving blade at different times during cutting 20 mm diameter branches
由图12挤压阶段A3B3(对应图13a)可知,动刀片刀刃部分开始接触、挤压树枝,树枝发生弹塑性变形,对刀刃部分产生反作用力,动刀片等效应力增加。
由图12切入剪切阶段B3C3(对应图13b)可知,动刀片刀刃部分切入树枝,树枝产生变形出现切口,等效应力迅速增加,达到整个切割过程的最大值,这是由于树枝切口包裹刀刃部分,刀刃部分受力集中,产生了较大的集中应力[27-28],G3为应力集中点,应力集中对构件的疲劳寿命影响很大,容易造成刀具刀刃处局部疲劳破损,可能出现刀具崩刃、断裂等现象,为防止刀具因应力集中造成的破坏,可以对刀具刀刃部分作喷丸、氮化处理,增强刀具表面疲劳强度,也可以通过改变刀具的外形降低应力集中系数。随着动刀片不断切入树枝,动刀片与树枝的接触面积增大,刀刃处的应力集中消失,应力迅速下降并趋于均匀,等效应力曲线平稳波动,这是由于树枝在动刀片的剪切、挤压作用下,出现裂纹萌生和扩展,在此过程中树枝在裂纹萌生时受力最大,在裂纹扩展时力值迅速下降[29],而树枝断裂过程是树枝受力和裂纹萌生扩展交替进行,故等效应力曲线平稳波动。
由图12稳定剪切阶段C3D3(对应图13c)可知,C3D3与曲线段B3C3相似,树枝断裂过程是树枝受力和裂纹萌生扩展交替进行,曲线继续波动。
由图12剪断阶段D3E3(对应图13d)可知,此阶段从树枝残留小部分断口到树枝完全断裂,掉落树枝部分在动刀片刀刃部分作用下与刀具迅速脱离,动刀片等效应力迅速下降,达到此阶段的最低点,但不为0,这是由于在树枝断裂时,动刀片仍与树枝固定一端接触产生轻微的挤压作用。
由图12树枝振动阶段E3F3(对应图13e)可知,树枝已经断裂,动刀片继续向下运动,但还未完全穿过树枝截面,树枝固定一端断口略不平整,只有少部分断口与刀具接触,接触面积少,同时树枝固定一端存在小幅度摆动,树枝与刀具存在间断性接触,故等效应力在达到最低点后出现近似直线的波动。
3.2 树枝应力分析
图14为20 mm直径树枝下树枝等效应力-时间曲线,图15为20 mm直径树枝下不同时刻树枝等效应力分布。由图14、15可知:切割过程中树枝等效应力总体先增加后减少,且伴有等效应力的突升突降,在树枝断裂时等效应力迅速下降,在达到最低点后开始小幅度波动。树枝最大等效应力出现在树枝切口附近,应力值为95.81 MPa。此外10和15 mm直径树枝下树枝最大等效应力分别为111.80和121.94 MPa。

图14 20 mm直径树枝的树枝等效应力-时间曲线Fig. 14 Equivalent stress-time curve of branches for 20 mm diameter branches
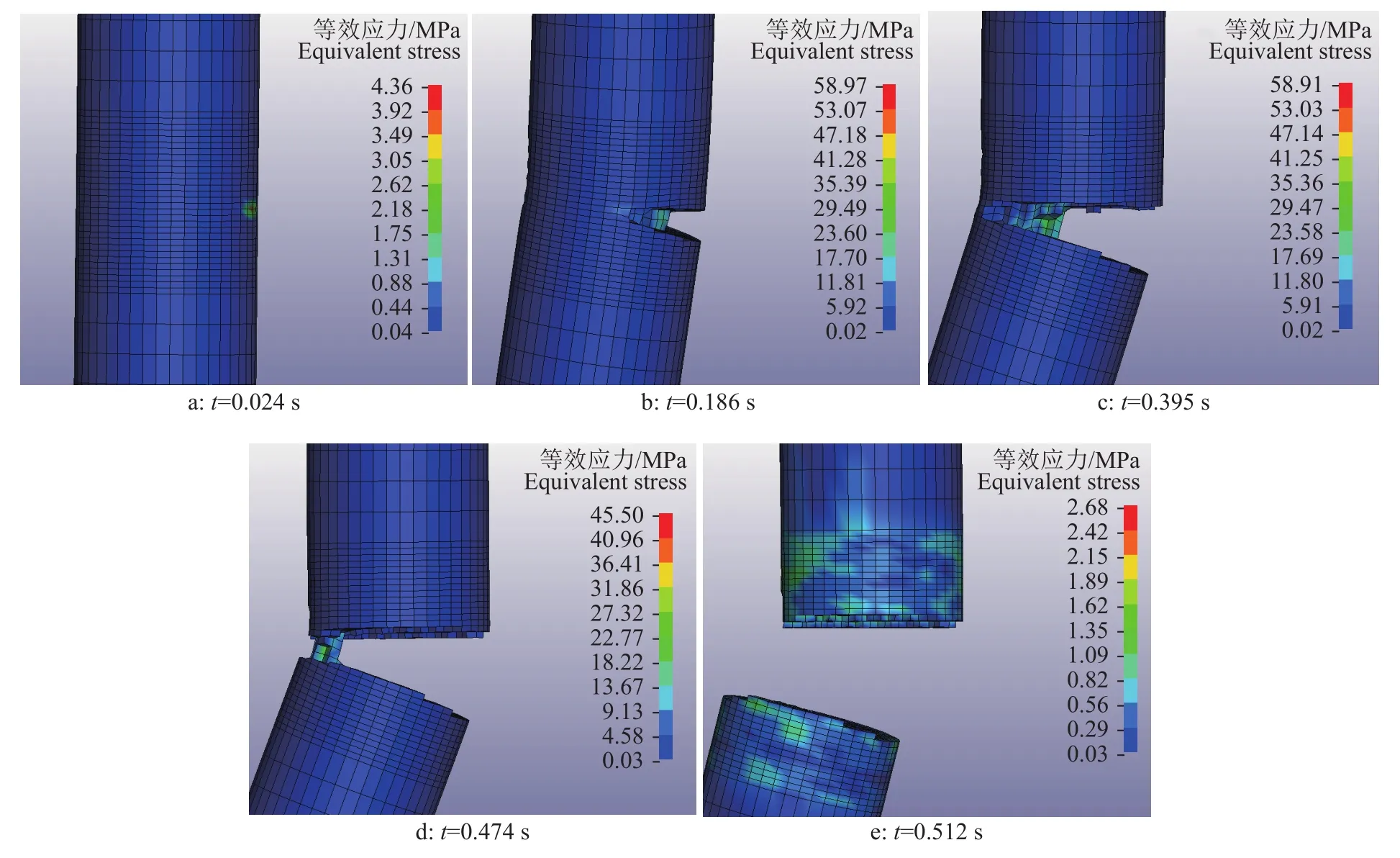
图15 切割20 mm直径树枝不同时刻树枝等效应力分布Fig. 15 Equivalent stress distribution on branches at different times during cutting 20 mm diameter branches
由图14挤压阶段曲线段A4B4(对应图15a)可知,树枝受到动刀片刀刃部分和定刀的挤压后发生弹塑性变形,树枝等效应力增加。
由图14切入剪切阶段曲线段B4C4(对应图15b)可知,动刀片刀刃部分切入树枝,当树枝内应力超过其屈服极限时,树枝出现切口产生变形,等效应力迅速增加,达到整个切割过程的最大值,这是由于此阶段刀刃部分率先与树枝接触,树枝表面形状急剧变化,出现切口,切口处应力局部增高,产生较大集中应力,G4为应力集中点。随后树枝切口扩大,树枝倾斜程度不断增加,掉落树枝部分并不是稳定向下倾斜运动,而是在来回摆动中运动,树枝受力不均,故树枝等效应力曲线会出现突升突降现象。
由图14稳定剪切阶段曲线段C4D4(对应图15c)可知,C4D4与曲线段B4C4相似,掉落树枝部分在来回摆动中向下运动,曲线段继续突升突降。
由图14剪断阶段曲线段D4E4(对应图15d)可知,此阶段树枝从残留小部分断口到完全断裂,树枝切口受到动刀片的剪切、挤压作用逐渐消失,树枝固定一端与动刀片后刀面接触受到轻微的挤压作用,故树枝等效应力迅速下降,达到此阶段的最低点。
由图14树枝振动阶段E4F4(对应图15e)可知,此阶段树枝已经断裂,但动刀片还未全部穿过树枝截面,树枝固定一端因小幅度摆动,与刀具间断性接触,故等效应力在达到最低点后开始小幅度波动。
3.3 定刀应力分析
图16为20 mm直径树枝下定刀等效应力-时间曲线,图17为20 mm直径树枝下不同时刻定刀等效应力分布。由图16、17可知:切割过程中定刀等效应力总体先增加后减少,当等效应力达到最大值后,开始下降至最低点,然后小幅度波动。定刀最大等效应力出现在定刀切口附近,应力值为31.41 MPa,远小于刀具材料SK-5的屈服极限应力930 MPa,说明定刀在切割树枝时不会发生失效。此外10和15 mm直径树枝下定刀最大等效应力分别为25.54和34.80 MPa,不会发生失效。
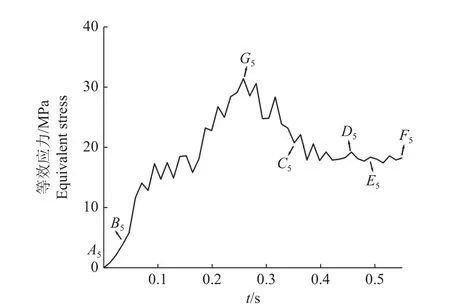
图16 20 mm直径树枝的定刀等效应力-时间曲线Fig. 16 Equivalent stress-time curve of fixed knife for 20 mm diameter branches
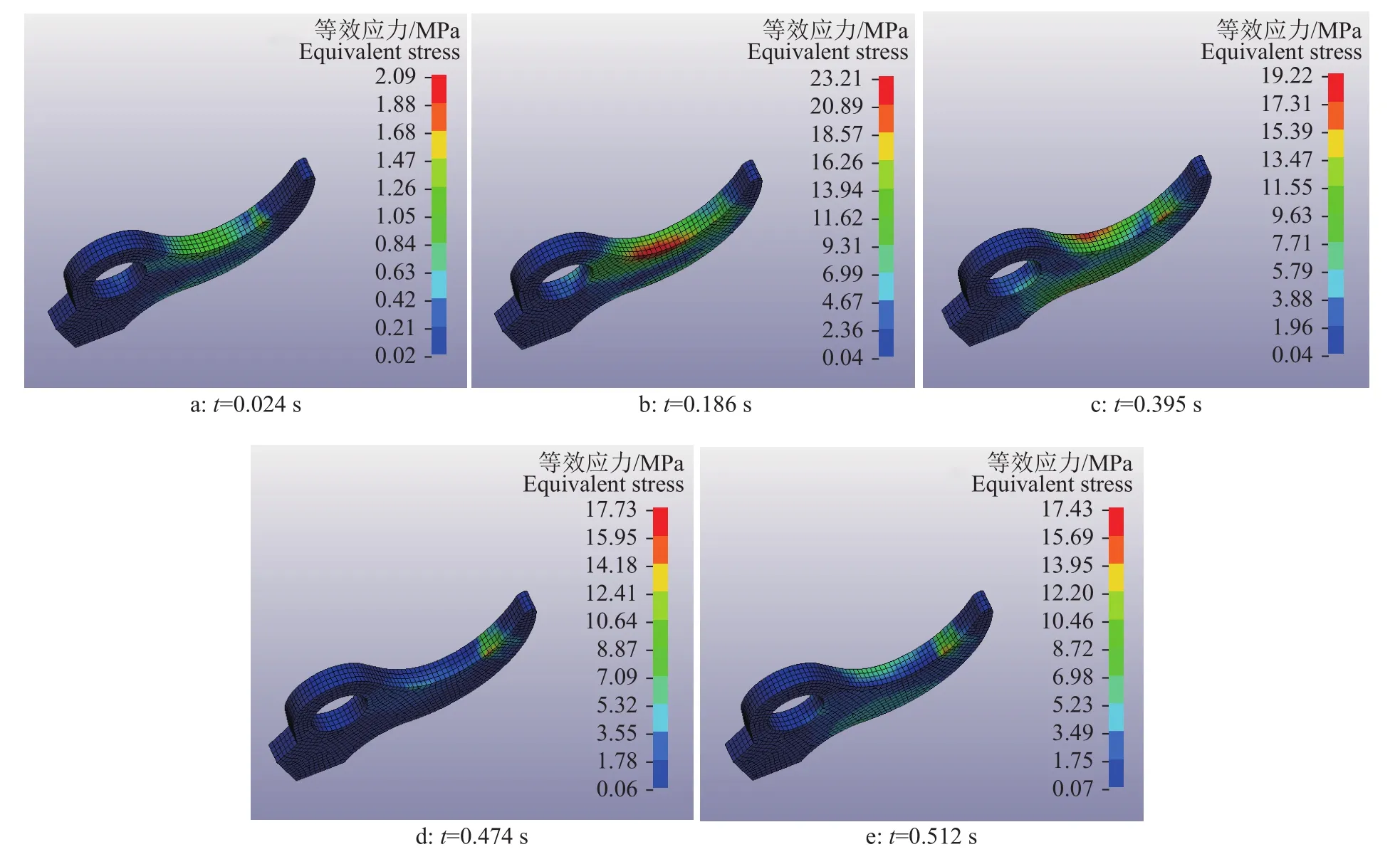
图17 切割20 mm直径树枝不同时刻定刀等效应力分布Fig. 17 Equivalent stress distribution on fixed knife at different times during cutting 20 mm diameter branches
由图16挤压阶段曲线段A5B5(对应图17a)可知,定刀受到动刀片施加于树枝作用力的挤压,定刀等效应力增加。
由图16切入剪切阶段曲线段B5C5(对应图17b)可知,动刀片开始切入树枝,树枝切口包裹刀刃部分,定刀受到动刀片施加于树枝作用力的挤压增强,定刀等效应力增加,同时动刀片会挤开两侧的树枝,掉落树枝部分在切口处发生弯曲,对定刀切口与刀背相交附近产生作用,此处同时受树枝挤压和树枝弯曲的作用,定刀切口附近应力局部增高,产生应力集中,等效应力达到最大值,G5为应力集中点。随着动刀片切入深度的增加,在动刀片刀刃倾角的影响下,刀刃部分受到的挤压力和摩擦力减小[30],故定刀受到动刀片施加于树枝作用力的挤压同样减小,又由于树枝在切割过程中一直处于小浮动摆动状态,定刀与树枝存在间断性接触且受力不均,定刀等效应力波动下降。
由图16稳定剪切阶段曲线段C5D5(对应图17c)可知,C5D5与曲线段B5C5相似,定刀受到动刀片施加于树枝作用力的挤压减小,同时定刀与树枝存在间断性接触且受力不均,等效应力继续波动下降。
由图16剪断阶段曲线段D5E5(对应图17d)可知,由于树枝处于断裂过程,定刀受到掉落树枝部分的压缩、挤压作用逐渐消失,仅轻微受到动刀片后刀面施加于树枝固定一端作用力的挤压,故树枝等效应力缓慢下降,达到此阶段的最低点但不为0。
由图16树枝振动阶段E5F5(对应图17e)可知,树枝已经断裂,但动刀片还未完全穿过树枝截面,因树枝固定一端小幅度摆动,定刀与其间断性接触,故等效应力在达到最低点后开始小幅度波动。
4 结论
1)树枝切割过程可分为5个阶段:挤压阶段、切入剪切阶段、稳定剪切阶段、剪断阶段、树枝振动阶段。
2)实际试验切割力比仿真试验略大,当树枝直径分别为10、15和20 mm时,刀具实际峰值切割力比仿真峰值切割力分别增加18.9、38.8和61.0 N,相对误差分别为7.8%、6.5%和6.6%,实际试验与仿真试验的刀具峰值切割力最大相对误差为7.8%,平均相对误差为7.0%,实际试验与仿真试验所得切割力曲线吻合,树枝切割过程仿真模型准确。
3)切割过程中动刀片、树枝和定刀最大等效应力出现在刀刃、树枝和定刀切口附近。10、15和20 mm直径树枝下动刀片最大等效应力分别为84.35、104.26和132.86 MPa,树枝最大等效应力分别为111.80、121.94和95.81 MPa,定刀最大等效应力分别为25.54、34.80和31.41 MPa,动刀片、定刀最大等效应力远小于刀具材料屈服极限,刀具不会发生失效。

