基于轨迹提取算法的视频关联动作跟踪仿真

龙 年

(湖北工业大学 工程技术学院, 武汉 430068)

视频跟踪是处理图像序列、 探究运动目标规律、 为人类提供决策数据支持的科学技术, 在国防建设、 航空航天等领域应用广泛. 采集外界环境信息中包含静止与运动的物体, 其中运动物体关联动作涵盖人们感兴趣内容的几率更高[1], 目前视频跟踪技术面向运动关联动作已有许多研究. 关联动作跟踪包括评估目标状态、 匹配更新目标形态等步骤, 因此跟踪算法在性能上通常需满足鲁棒性、 精准性和实时性[2]3个条件. 鲁棒性表示跟踪时的抗干扰性能, 在某些跟踪失败场景内需具备自修复能力; 精准性表示跟踪要满足一定的精度, 提供出目标的大致方位与姿态信息; 实时性表示跟踪方法要具备较快的运算效率, 保证跟踪结果的有效性. 针对视频跟踪问题, 文献[3]设计了一种浅层前向自学习卷积网络获得目标区域局部卷积特征, 推算空间信息颜色直方图特性, 利用归一化加权策略构成目标表观描述, 计算出目标模板和候选目标间的相似度, 估计目标具体方位; 文献[4]采用快速重采样粒子滤波算法, 用准Monte Carlo方法确定序列属性, 使用背景差分算法消减计算视频监控图像帧, 组建动态粒子滤波器并通过颜色分布特征实施跟踪. 但以上两种方法在目标区域广泛、 外观信息量较少状态下, 很难获得目标的外观特征, 导致跟踪准确性较低, 算法具有一定的局限性.

基于此, 本文提出一种基于轨迹提取算法的视频关联动作跟踪方法. 首先, 引进多元组定义, 组建多元组轨迹提取模型, 关联规则挖掘视频轨迹特征并采取数据融合; 其次, 计算关联动作轨迹分布场值, 获得视频关联动作轨迹特征; 最后, 用多粒度滤波算法实现关联动作跟踪, 并通过仿真实验证明算法的可靠性与实用性.

1 基于轨迹提取算法的视频关联动作分析

轨迹提取即获得每帧视频内各运动目标的方位数据[5], 方便了解视频中目标对象的关联动作规律, 提高后续关联动作的跟踪准确性. 在轨迹提取算法前提下, 综合视频场景真实需求, 引入多元组概念, 创建多元组轨迹提取模型[6-7]. 多元组是目标数量的有限序列, 一般用于定义数学对象的实际成分. 基于多元组定义, 设计如下多元组表达式：

TR={Fl,Fr,Cen,Rect,Cont,Or,V,Oc},

(1)

其中Fl为目标标签, Fr是视频帧号码, Cen为轨迹提取目标质心坐标, Rect是目标的外接矩形, Cont为轮廓参变量, Or为目标关联动作运动方向,V是目标运动速率, Oc用于定义视频关联动作中是否产生遮挡现象.

在多元组轨迹提取模型计算环境下, 为得到高精度关联动作细节, 首先计算运动动作视频图像特征分布矢量化集合[8], 将视频图像分割的支持向量机临界值记为

(2)

(3)

其中：d(i,j)为视频图像的灰度像素集合；h为铰链损失函数；Z(i)表示视频区域特征匹配范围的模板匹配数值, 用于描述视频关联动作图像的Gibbs先验能量函数, 并与运动视频特征分量进行动态融合[9], 获取视频关联动作的特征分布情况, 用公式表示为

(4)

式中f表示视频图像灰度像素级,xi和xj表示灰度像素点.

设视频图像视觉范围大小为M×N, 按动作视频视觉颜色系统值进行像素特征分离, 用公式表示为

(5)

其中βi为像素特征分离值, dist(xi,xj)为像素点分布指数.

通过上述过程, 对视频轨迹特征实施关联规则挖掘, 将不同属性的关联动作投射至关联分布区域内, 并采取数据融合.使用虚拟视景重构策略完成视频关联动作特征分析, 并利用矢量量化策略完成视频动作分块检测[10-11], 将视频图像像素点子集数值记为

I(x)=J(x)t(x)+A(1-t(x)),

(6)

其中A为视频图像关联动作三维尺度数据,t(x)为视频图像采样时间间隔,J(x)为视频图像像素点连通分量.用活动轮廓套索模型实施关联动作特征提取, 按运动视频轨迹分布特征值, 获取关联动作轨迹提取实时输出值为

(7)

其中u表示关联动作轨迹特征分量处于梯度方向的像素强度,σ表示视频旋转算子.最后计算出关联动作轨迹分布场值, 完成视频关联动作轨迹特征分析：

dft+1(i,j,k)=ρdft(i,j,k)+(1-ρ)dft-1(i,j,k),

(8)

其中ρ表示轨迹实时提取相关性指数,k表示轨迹提取次数.

2 基于多粒度滤波的视频关联动作跟踪方法

明确关联动作规律后, 可更细致地描绘出关联动作的具体特征.为实现准确关联动作跟踪目标, 在粒计算概念下, 设计一种基于多粒度滤波的视频关联动作跟踪方法.粒子是粒计算中的基础单位, 其核心为： 设定论域S内的关系R, 符合R:S→P(S),P(S)是论域S的幂集,R的划分可呈现出等价关系或约等关系,ei是粒度内的一个信息粒子.如果存在一个数据集K=(U,Q),B∈Q为U中的等价关系,U/B={z1,z2,…,zn}, 则B的粒度是GD(B), 可表示为

(9)

使用Fourier变换将传统卷积计算变换为点乘计算[12].若输入的关联动作特征为x,g为相关滤波器, 则按卷积理论可得

(10)

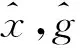
实施多粒度滤波器训练过程中, 首先需设定一个预期输出值y.如果目标样本是x′, 则按卷积性质可得：

(11)

训练后的卷积核为

(12)

根据上述流程对图像采取循环卷积操作时能有效减少跟踪算法的计算难度[13-14].对一张n×n大小的图像进行传统卷积操作与Fourier变换的点乘计算, 两种方法的复杂度分别为O(n4)和O(n2lgn).

利用卷积特征, 用第i个输入迅速获取相对的标签yi, 将相关滤波器视为一个分类器[15], 设f(xi)=yi, 则可将训练过程等同于如下目标函数：

(13)

其中：δ表示模型参变量；λ表示避免过拟合的正则项指数；G表示损失函数, 计算公式为

G(f(δ,xi),yi)=(yi-f(δ,xi))2.

(14)

函数f(xi)有多种表达形式, 在式(14)中表示线性操作, 以此完成视频关联动作跟踪优化, 获得下列闭合解：

δ=(XTX+λI)-1XTy,

(15)

其中X的行向量表示训练样本,y表示相对的标签数据,I表示单位矩阵.

(16)

其中Area为重叠指数.

每个粒度的轨迹平滑度在一定程度上表现出跟踪结果的真实性.利用欧氏距离[19]推导出两个边界最小矩阵的变换情况:

(17)

并以此获得每个粒度的轨迹波动水准:

(18)

(19)

其中κ(xi,xj)表示核矩阵中对应的元素,α表示跟踪次数.

3 仿真实验

实验环境为奔4处理器, 2 GB内存的计算机, 使用MATLAB7.1仿真环境对关联动作视频监控进行实验研究. 实验数据源自某监控视频数据库, 选取第200帧～第500帧共300帧图像进行仿真实验, 图像分辨率为380×280, 监控中有两辆车进行不规则运动, 且活动区域较小.

图1(A),(B)为视频监控图像, (C),(D)分别为本文方法下的关联动作跟踪结果, 矩形框表示检测目标区域, 数字表示跟踪目标的编码, 圆圈表示帧目标跟踪状态估计的方位. 由图1可见, 在视频监控区域范围较大、 且包含无关目标的情形下, 本文方法能有效提取多个目标特征, 准确跟踪一个或多个目标关联动作, 可靠性极强.

图1 本文方法视频关联动作跟踪结果Fig.1 Video association motion tracking results of proposed method

为进一步表明本文方法的实用性, 将本文方法与文献[3]提出的多特征融合方法和文献[4]提出的重采样粒子滤波方法进行对比实验, 3种方法在视频监控画面2中的跟踪偏差如图2所示, 跟踪偏差由跟踪目标中心实际坐标和目标估计方位的欧氏距离获得.

图2 3种方法在监控视频画面2中的跟踪误差Fig.2 Tracking error of three methods in monitoring video picture 2

由图2可见： 目标关联动作跟踪过程中, 多特征融合法要符合一对一关联约束, 不能有效处理目标的消失、 遮挡、 分离等复杂运行状况, 跟踪偏差较大; 重采样粒子滤波法视频动作跟踪运算繁琐, 需要计算镜头噪声或静止背景内噪声, 导致方法自适应能力较差, 跟踪偏差也较大. 虽然视频监控内仅包含两个跟踪目标, 但由于其外观相似度较高, 且场景与光线不断变换, 因此多特征融合法和重采样粒子滤波法的跟踪结果中具有目标轨迹碎片, 跟踪偏差较大. 在视频监控区域较广、 目标相似度高的状态下, 本文方法跟踪偏差远低于对比方法, 可实现及时有效地视频关联动作跟踪. 因为本文方法使用轨迹提取算法, 分析运动动作视频图像特征分布, 获得精准的跟踪轨迹, 跟踪偏差较小.

分析3种方法跟踪的时效性, 不同方法的跟踪速率结果列于表1. 由表1可见, 随着实验次数的增加, 不同方法跟踪每秒处理帧数速率变化幅度随之减小. 当实验次数为80次时, 本文方法的视频关联动作跟踪速率为14.9帧/s, 多特征融合法的视频关联动作跟踪速率为5.9 帧/s, 重采样粒子滤波法的视频关联动作跟踪速率为8.3帧/s. 实验结果表明, 本文方法的视频关联动作跟踪速率较高, 且随着实验次数的增加, 基本维持不变, 具有更优的跟踪性能. 而对比方法跟踪速率均不同程度地低于本文方法, 易产生跟踪延迟与卡顿现象, 无法保障关联动作跟踪的连贯性与准确性.

表1 3种方法视频关联动作跟踪速率对比结果

综上所述, 针对已有视频关联动作提取精度较低、 时效性较差等问题, 本文提出了一种基于轨迹提取算法的视频关联动作跟踪方法. 该方法在轨迹提取概念上, 融入多粒度滤波思想, 有效处理传统视频跟踪方法的特征单一性问题, 具有较强的实用性. 实验结果表明, 本文方法的监控视频画面跟踪偏差较小, 可实现及时有效的视频关联动作跟踪, 且本文方法的视频关联动作跟踪速率较高, 具有更优的跟踪性能.