基于GWO-SVM的石化旋转机械轴承故障诊断1
莫常春,刘美,费继友,张清华,张斐,吴斌鑫,3,周正南,3
(1.广东石油化工学院 自动化学院,广东 茂名 525000;2.大连交通大学 机车车辆工程学院,辽宁 大连 116028;3.吉林化工学院 信息与控制工程学院,吉林 132022;4.东莞理工学院 机械工程学院,广东 东莞 523419 )
故障诊断是确保石化机组“安、稳、长、满、优”运行非常重要的步骤[1]。石化现场事故的统计数据显示,因轴承故障而引发的事故占比很大,因此有必要对旋转机械轴承进行故障诊断。在故障诊断领域,特征参数法比较常用,波形指标、峰值指标、裕度指标、脉冲指标、峭度指标等一系列时域无量纲指标由于具有不受现场工况影响的特性,在故障特征提取中得到广泛应用[2]。但无量纲指标在某些故障数据间存在重叠,对某些故障特征不是很敏感。熊建斌等[3]提出了互无量纲指标的数据处理方法,解决了传统无量纲指标存在的不足,并有效应用于石化机组故障诊断。覃爱淞等[4]通过遗传编程构建出了具有最佳分类能力的新无量纲指标,并将其应用到石化机组的故障诊断中,在轴承故障诊断中取得了相当好的效果。Chapelle等[5]在提出了一种机器学习算法——支持向量机(SVM),目前SVM在故障诊断领域得到了广泛运用,故障诊断分类效果较好。但是影响SVM模型分类性能的惩罚因子C和核函数参数γ相关文献并没有给出确切的方法。基于此,本文提出了一种基于互无量纲指标和灰狼算法优化的SVM模型的石化旋转机械轴承故障诊断方法[6]。本文采用灰狼算法(GWO)对SVM进行参数优化,可避免算法出现局部最优、收敛性差、搜索效率低等问题,有效地应用于石化机组11kW5级离心风机滚动轴承的故障诊断。
1 互无量纲指标
传统无量纲指标之间存在严重的数据重叠,再加上现有的无量纲指标只对滚动轴承的部分故障特性敏感,导致故障辨识分类效果并不理想。互无量纲指标在传统无量纲的基础上进行改进,采用一种新的无量纲数据融合计算方法,构造出新的故障特征证据体——互无量纲指标,互无量纲指标克服了传统的无量纲指标数据重叠的问题,且对故障特征更加敏感,同时互无量纲指标不受载荷和转速的变化影响,因此互无量纲指标在故障诊断领域得到很好的应用[7]。
(1)
式中:р(s)和р(y)分别为s和y的概率密度函数。
式(1)取不同系数,构建出5个不同的互无量纲指标,分别为
(2)
(3)
(4)
(5)
德国前总理格哈德·施罗德说,习近平主席是一位远见卓识的改革家。他把马克思主义原理与中国实际结合,紧随时代进行创新,提出了雄心勃勃的改革计划,涵盖了各个领域。实践证明行之有效,深得人心,是实现中国梦的基本方略,也是开辟人类更加美好未来的行动指南。巴西中国问题研究所所长罗尼·林斯认为,中国共产党不仅能独立自主有效地治理自己的国家,而且将以更加积极的姿态参与全球治理。
(6)
2 灰狼算法优化支持向量机
2.1 支持向量机
支持向量机因其能够有效且可靠地解决分类问题,在旋转机械故障诊断中得到广泛应用[8]。最主要的算法思想是通过核函数将低维线性不可分样本映射到高维空间,寻找一个超平面对样本进行分割,分割的原则是实现间隔最大化,从而达到分类目的[9]。
设有n个线性可分的样本(x1,y1),(x2,y2),…,(xn,yn),x∈Rμ,y∈{+1,-1}, ,其中μ代表数据的维度,y=+1和y=-1分别表示样本数据的两个类别,分类超平面如式(7)表示:
WTx+b=0
(7)
对于寻求分类超平面,通过引入拉格朗日乘数法理论,再转变成对偶问题进行求解,如式(8)所示。
(8)
(9)
其中本文支持向量机算法采用的核函数为RBF核函数为
(10)
由此可见,影响SVM模型分类精度的两个参数主要是惩罚因子C和核函数参数γ[10]。目前,这两个参数的选取还没有相关文献给出具体的解决办法。因此,本文引入灰狼算法对支持向量机的两个重要参数进行优化,从而构建出辨识分类精度以及运行效率更高的GWO-SVM石化旋转机械滚动轴承故障诊断模型。
2.2 灰狼算法(GWO)
GWO算法是模拟自然界中灰狼群体的社会等级机制和捕猎行为而衍生出来的一种新型群体智能优化算法,GWO算法能够实现目标参数优化,具有较好的收敛性等特点[11]。算法中狼群有α、β、δ、ω四个等级,如图1所示。
图1 灰狼等级层次制度
GWO算法中,α(头狼)为待求问题最优解,β(二级狼)和δ(三级狼)分别记为次优解和次次优解,其余解(剩下的狼)均设为ω。狼群中把α、β、δ三头狼作为初始值带领狼群在空间寻找猎物(最优解)或者不断逼近(不断迭代)。
捕捉猎物 (参数寻优)时,狼群对猎物进行包围,不断逼近猎物,寻找全局最优解,且不断更新位置,位置表示如下:
X(t+1)=Xp(t)-W·[B·Xp(t)-X(t)]
(11)
式中:X(t)为灰狼目前所在位置;Xp为猎物位置;B为摆动因子,
B=2r2;W为收敛因子,W=2ar1-a;a为迭代控制系数,a=2-2t/Nmax;r1和r2为[0,1]之间的随机数;t为灰狼算法当前的迭代次数;Nmax为最大迭代次数。
GWO算法中,狼群中α、β、δ起到引导的作用,自动更新个体位置。
X1=Xα-A1·[B1·Xα(t)-X(t)]
(12)
X2=Xβ-A2·[B2·Xβ(t)-X(t)]
(13)
X3=Xδ-A3·[B3·Xδ(t)-X(t)]
(14)
Xp(t+1)=(X1+X2+X3)/3
(15)
式中:Xα为最优解(头狼α)的位置;Xβ和Xδ分别为次优解(二级狼β)和次次优解(三级狼δ)的位置;A1、A2、A3和B1、B2、B3为随机数产生的不同系数;X1、X2、X3为狼群中领导层更新后的位置。
灰狼捕猎成功,获得最优解,灰狼狩猎行为主要以式(11)中值所体现,迭代次数从2线性减小至0完成,当W≤1时,灰狼集体出动攻击猎物,相当于算法局部搜索;当W>1时,灰狼算法进行全局搜索。
2.3 实验背景与数据来源
为了验证GWO-SVM故障诊断模型的可行性,通过对广东省石化装备故障诊断重点实验室石化多级离心风机故障诊断平台轴承采集的实验数据进行验证。多级离心风机故障诊断平台由变频电机、负载控制器、变速箱、多级离心风机、EMT390振动数据采集器以及各种故障件组成,其中滚动轴承实验故障件如图2所示。

图2 石化旋转机械滚动轴承故障件
实验主要以轴承常见的4种不同故障 (轴承缺滚珠、轴承内圈磨损、轴承外圈磨损、正常轴承)开展研究,数据采集与处理的具体过程如下。
(1)使用EMT390数据采集器在多级离心风机垂直部位采集4种类型的机壳振动加速度数据,每种故障采集2次,每次50组数据。其中,每一组数据有1024个机壳振动加速度,4种故障类型的原始振动波形如图3所示。

图3 正常轴承以及轴承不同故障类型信号时域
(2)使用数据采集器的数据管理系统将采集到的数据保存为mat文件。
(3)用MATLAB对所采集的各种故障数据进行处理,构造互无量纲指标,再将5个互无量纲指标构成的数据集矩阵进行编号。
(4)从采集的滚动轴承原始数据中随机抽取50组数据,组成一个含有200组故障数据的训练集,通过matlab中的ramdom函数随机选取50%的数据集作为模型训练集,另外50%作为测试集。滚动轴承4种状态下的时域图如图3所示。
本文提出一种基于互无量纲指标和GWO-SVM的故障诊断方法,故障诊断具体流程如下:(1)把样本数据集分为两部分,一部分为训练集,另一部分为测试集。(2)选取训练集数据作为SVM的输入,然后用灰狼算法对支持向量机参数C和γ进行优化,更新适应度,狼群数量设为30,设置最大迭代次数为600,求解C和γ的最优值,得到训练出具有较高辨识能力的SVM 分类模型。(3)将石化旋转机械轴承测试集输入GWO-SVM模型进行故障辨识分类。(4)输出诊断结果。
3 实验结果分析
为了验证GWO-SVM轴承故障诊断模型的可行性和优越性,将SVM模型与遗传算法优化支持向量机(GA-SVM)模型同本文提出的GWO-SVM模型进行比较。实验数据选取正常轴承、轴承外圈磨损、轴承内圈磨损以及轴承缺滚珠4种故障类型,并分别随机抽取数据80组,总共的样本数为320组。通过MATLAB中的random函数随机选取数据选取50%(160组)作为故障诊断模型的训练集,剩下的50%(160组)作为故障诊断模型的测试集,传统支持向量机(SVM)、遗传算法优化支持向量机(GA-SVM)、灰狼算法优化支持向量机(GWO-SVM)这3种算法辨识分类结果如图4~6所示,这3种算法故障诊断结果性能指如表1所示。

图4 SVM模型故障诊断结果 图5 GA-SVM模型故障诊断结果 图6 GWO-SVM模型故障诊断结果
由表1可知,在对正常轴承、轴承外圈磨损、轴承内圈磨损以及轴承缺滚珠4种故障类型数据进行实验时,从算法的轴承故障辨识分类准确度来看,GWO-SVM模型的轴承故障辨识分类的准确率明显高于SVM和GA-SVM这两种算法。在算法运算时间上来看,GWO-SVM算法运算效率明显高于SVM和GA-SVM这两种算法,算法运行时间大大缩短。由此可知,本文提出的灰狼算法优化的支持向量机在性能方面比支持向量机以及遗传算法优化支持向量机的故障诊断效果优越,能有效地运用于大型石化旋转机械滚动轴承的故障诊断。
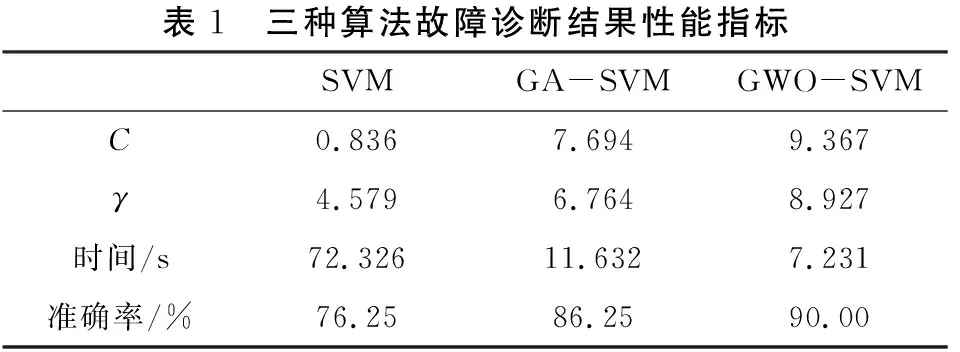
表1 三种算法故障诊断结果性能指标SVMGA-SVMGWO-SVMC0.8367.6949.367γ4.5796.7648.927时间/s72.32611.6327.231准确率/%76.2586.2590.00
4 结语
针对广东省石化装备故障诊断重点实验室石化多级离心风机故障振动信号非线性和非平稳性的特征以及支持向量机分类算法参数选择困难的问题,本文提出了一种利用灰狼算法优化支持向量机参数的方法,利用灰狼算法独有的全局优化能力对支持向量机两个重要参数进行选择优化。结果表明,本文所提出的算法在大型石化旋转机械轴承故障诊断中准确率高、运行时间短,为石化大机组滚动轴承故障诊断提供了一种切实可行的方法。

