中国东南沿海地区PWV直接转换模型研究
韦 云 王 迅 王 浩 李 黎 陈国栋 赵 伟
1 苏州科技大学地理科学与测绘工程学院,江苏省苏州市学府路99号,215009 2 苏州科技大学北斗导航与环境感知研究中心,江苏省苏州市学府路99号,215009
近年来,利用由GNSS技术获取的PWV时空变化趋势来预测降雨的方法成为国内外学者关注的重点[1-3]。传统的获取PWV的方法是利用由GNSS技术得到的对流层延迟(ZTD)减去干延迟(ZHD),得到湿延迟(ZWD),再利用ZWD推算得到PWV。计算ZHD需要的参数有测站处地面大气压(Ps)、测站纬度(θ)、测站大地高(H),ZWD与PWV之间的转换系数也要用到加权平均温度(Tm)、地面气温(Ts)等参数,参数越多,计算过程越复杂,会导致数据量大、计算效率低,且易产生误差累积等问题。因此,建立ZTD与GNSS-PWV之间的直接转换模型,以计算特定时段的PWV时序信息十分必要[4-6]。
本文基于2017年东南沿海地区18个GNSS站的观测数据,采用多元函数线性回归法建立该地区GNSS-PWV与ZTD、地面气温(Ts)、地面大气压(Ps)之间的直接转换模型,并利用模型预报2018年GNSS-PWV,以各站实测PWV为参考值,验证本文模型的预报精度。
1 数据来源及其相关性分析
1.1 数据来源
选取由江苏省气象局和中国地震局GNSS数据产品服务平台(http:∥www.cgps.ac.cn)提供的2017~2018年东南沿海地区18个GNSS站资料,主要包括PWV、ZTD、地面大气压(Ps)和地面气温(Ts)等,其中常州、黄山、蚌埠、武夷山4个气象站用于精度检验,其余14个测站用于建模,测站空间位置信息见表1,选取的18个GNSS站均匀分布于108°~122°E、19°~33°N区域,涵盖了东南沿海大部分地区。
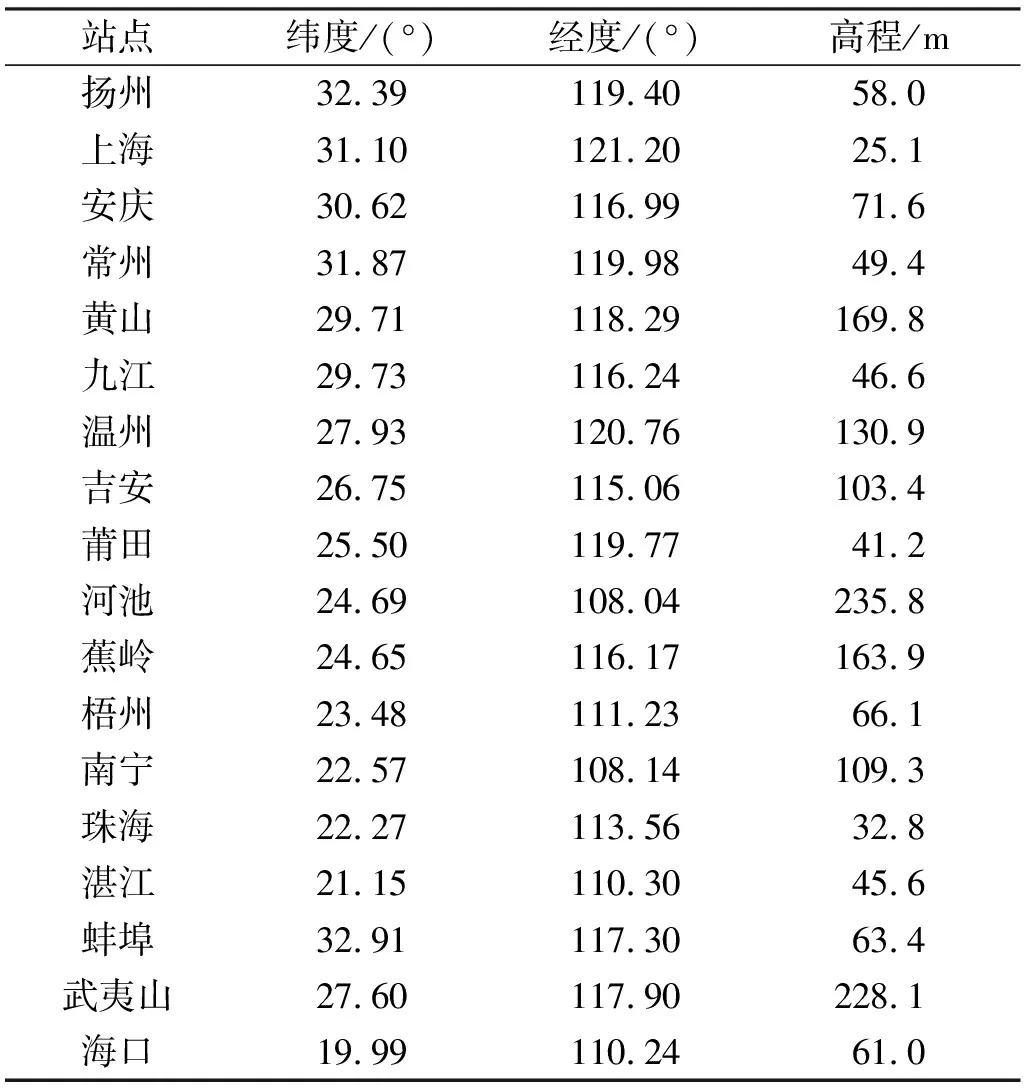
表1 GNSS测站空间位置信息
中国地震局GNSS数据产品服务平台采用Saastamoinen模型计算ZHD[7],其表达式为:
(1)
用ZTD减去ZHD获得ZWD,ZWD乘以转换系数Π便可得到GNSS-PWV:
(2)
式中,ρw为液态水密度,k′2、k3为大气折射常数,Rv为水汽气体常数,Tm为加权平均温度。
1.2 影响因子相关性验证
皮尔森(Pearson)相关系数R可用来描述2个变量之间的线性相关程度,R的绝对值越大,表明其相关性越强,在0.8~1.0之间表示极强相关,0.6~0.8之间为强相关,0.4~0.6之间为中等程度相关,0.2~0.4之间为弱相关,0.0~0.2则无相关性[8]。
PWV与ZTD、Ts、Ps之间的相关程度如图1所示,可以看出,ZTD与PWV的相关系数为0.98,为极强相关,表明ZTD对PWV值有极大影响;PWV与Ts的相关系数为0.78,为强相关;PWV与Ps的相关系数为-0.65,为负强相关。
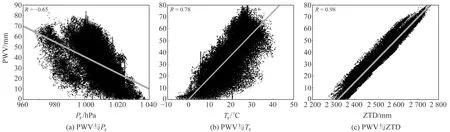
图1 相关性分析
表2为各变量间相关性统计结果,可以看出,各自变量之间也存在一定的线性关系。若建模选取的样本自变量之间本身就存在高度共线性关系,会导致线性回归模型不稳定,难以区分各自变量对模型结果的影响,因此需要对自变量进行共线性分析。
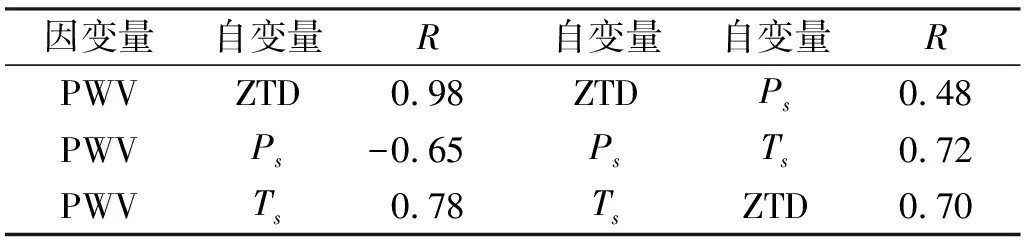
表2 相关性分析统计
本文利用方差膨胀因子(variance inflation factor,VIF)分析各自变量之间的共线性,其表达式为:
VIFi=1/(1-R2)
(3)
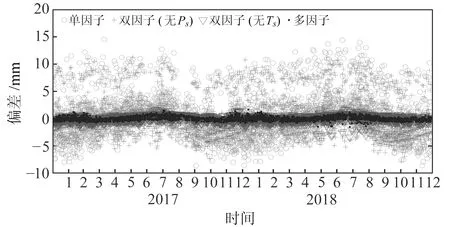
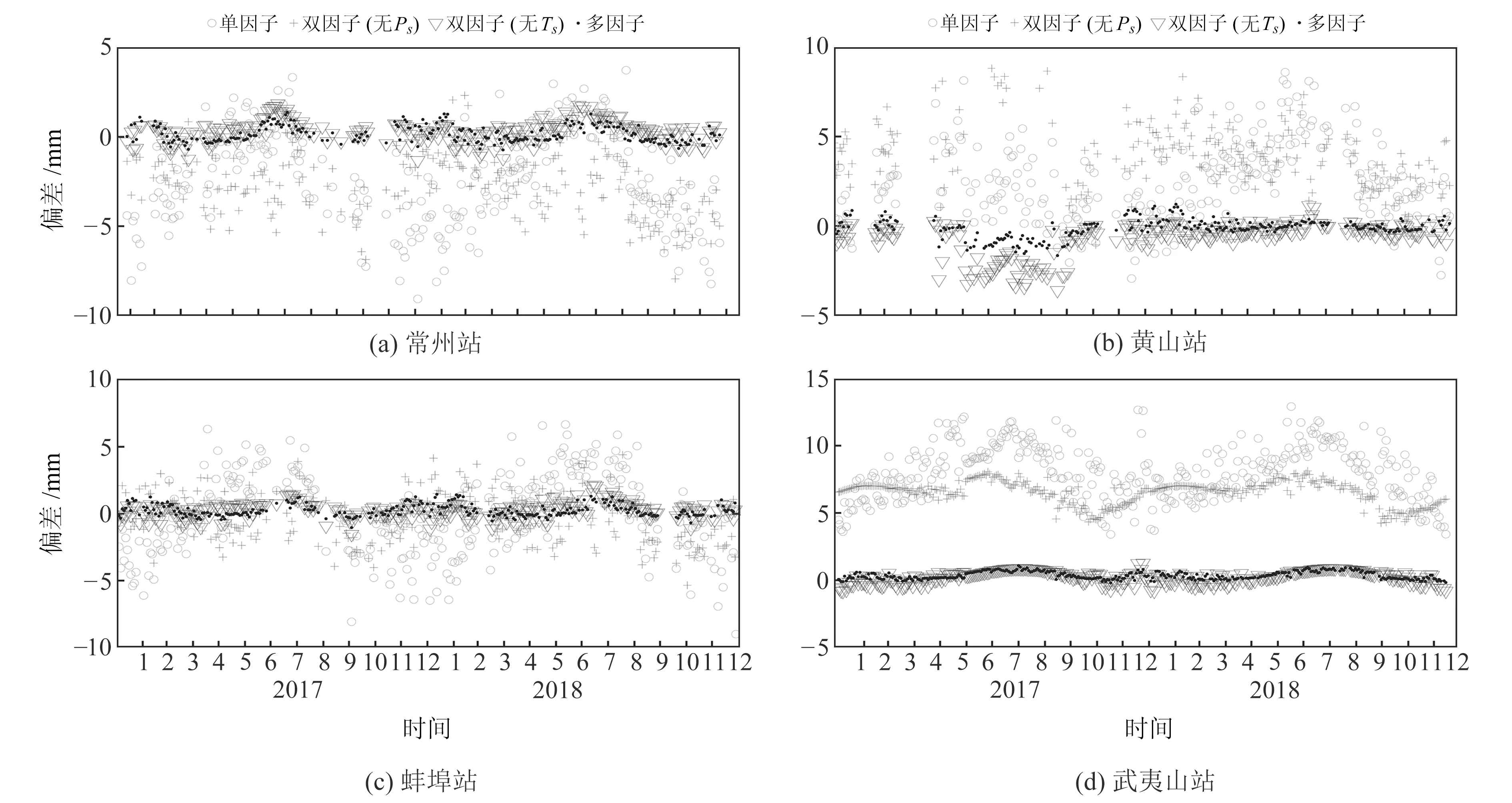
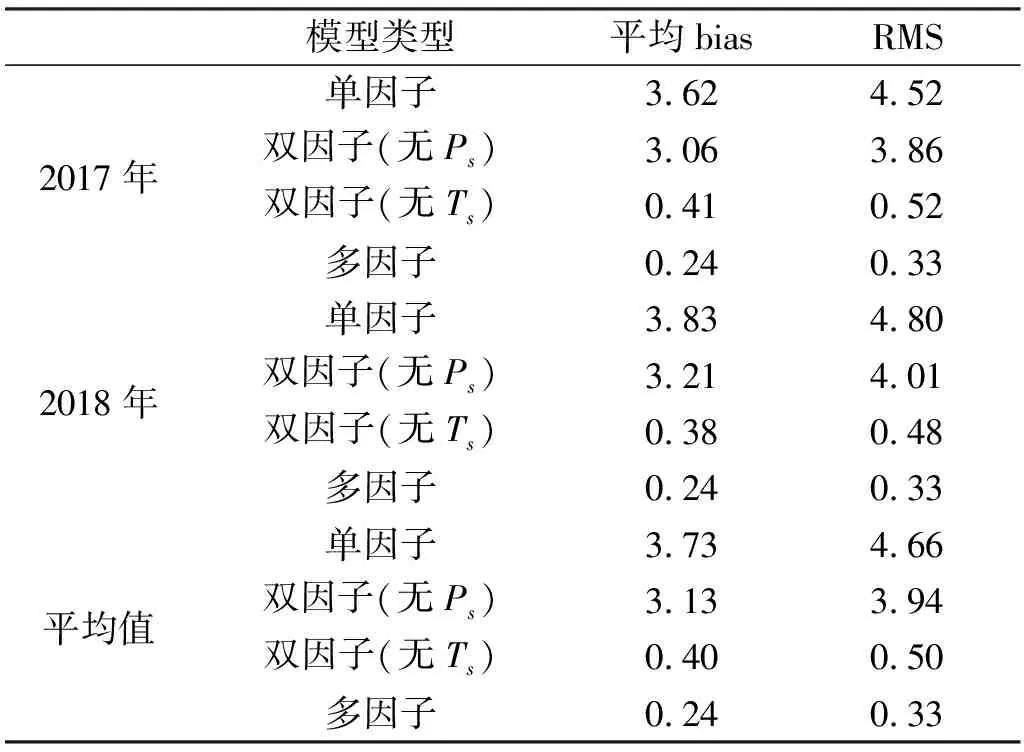
式中,R为自变量x与其余自变量作回归分析的复相关系数。通常认为,当0 利用多元函数线性拟合方法建立PWV直接转换模型。设多元线性回归模型为: y=β0+β1x1+…+βmxm+ε,ε~N(0,σ2) (4) 式中,y为因变量;x1、x2、…、xm为自变量;β0为常数项;β1、…、βm为回归系数,是与自变量无关的未知参数;ε为误差项[10],是均值为0、方差σ2>0的不可观测随机变量。若有n个独立观测数据,则可列出n个关于未知参数x1、x2、…、xm的方程: yi=β0+β1xi1+…+βmxim+εi εi~N(0,σ2),i=1,…,n (5) 则有: PWV转换模型可表示为: Y=Xβ+ε,ε~N(0,σ2En) (6) 式中,En为n阶单位矩阵。该线性回归模型可用最小二乘法原理求解,其中自变量的系数βi为最小二乘估计值。 2.1.1 多因子模型 基于PWV与ZTD、Ts、Ps的线性关系,PWV与其他参数函数的关系为: PWV=β0+β1ZTD+β2Ts+β3Ps (7) 将2017年14个测站的PWV与ZTD、Ts、Ps代入式(7),利用最小二乘法可得到多因子PWV的直接转换模型为: PWV=-13.380 5+0.162 9ZTD+ 0.074 1Ts-0.359 7Ps (8) 2.1.2 双因子模型 将2017年14个测站的PWV与ZTD、Ts代入式(7),得到基于ZTD和Ts的双因子PWV直接转换模型: PWV=-377.315 7+0.161 0ZTD+ 0.415 7Ts (9) 将PWV与ZTD、Ps代入式(7),得到基于ZTD和Ps的双因子PWV直接转换模型: PWV=3.335 4+0.165 8ZTD-0.3821Ps (10) 2.1.3 单因子模型 假设PWV和ZTD之间的线性关系为: PWV=β0+β1ZTD (11) 将2017年14个测站的PWV和ZTD代入式(11),得到基于ZTD的单因子PWV直接转换模型: PWV=-423.991 2+0.182 7ZTD (12) 利用2017年14个测站的数据建立PWV模型,分别将2017~2018年的数据代入所建模型中,计算得到PWV模型预测值,并与原始数据中的PWV实测值(作为真值)进行比较,验证模型的精度。 本文将PWV实测值减去PWV模型预测值,计算得到真值与预测值之间的偏差(bias),通过统计分析平均bias与RMS值来验证PWV模型的精度。图2为各PWV模型的bias变化趋势,可以看出,单因子PWV模型预测值与真值的bias基本在15 mm以内;双因子(无Ps)PWV模型预测值与真值的bias在10 mm以内;双因子(无Ts)PWV模型预测值与真值的bias在2 mm以内;多因子PWV模型预测值与真值的bias在1 mm以内,精度最高。2018年的数据未参与建模,PWV模型预测值及bias的变化趋势与2017年情况基本一致。 图2 2017~2018年不同PWV模型预测值偏差 图3为未参与建模的常州、黄山、蚌埠和武夷山等4个测站2017~2018年各PWV模型预测值bias。由图可知,常州站和蚌埠站基于双因子(无Ps)模型和单因子模型的预测值大部分大于真值,而基于双因子(无Ts)模型的预测值大部分小于真值,基于多因子模型的预测值则均匀分布于真值两侧;黄山站和武夷山站基于双因子(无Ps)模型和单因子模型的预测值均小于真值,基于双因子(无Ts)模型的预测值均大于真值,而基于多因子模型的预测值同样均匀分布于真值两侧。从bias的变化范围来看,4个测站的PWV偏差值与参与建模的PWV偏差值分布基本一致,各类模型的bias变化范围也与图2非常接近。 图3 2017~2018年各测站PWV模型预测值偏差 表3(单位mm)为各PWV模型预测值的平均bias和RMS统计结果,可以看出,基于单因子模型的RMS值为4.66 mm,平均bias为3.73 mm;加入Ts的双因子模型RMS值降至3.94 mm,平均bias为3.13mm,精度有小幅提升;加入Ps的双因子模型RMS值降至0.50 mm,平均bias为0.40 mm,精度大幅提高;同时加入Ps和Ts的多因子模型RMS值降至0.33 mm,平均bias降为0.24 mm,精度达到最高。 表3 全年PWV模型精度统计 由式(1)和式(2)可知,ZHD主要通过Ps计算得到,ZWD主要通过Ts及Tm计算得到,而Tm也由Ts计算得出。由于ZHD约占对流层延迟的80%~90%,加入Ps的双因子模型能提升ZHD的计算精度,而ZWD在ZTD中的占比较小,因此基于ZTD与Ps的双因子PWV模型的精度明显比基于ZTD和Ts的双因子PWV模型的精度高。 与基于ZTD、Ts和Ps的多因子PWV模型相比,基于ZTD和Ps的双因子PWV模型的精度稍低,但其RMS值有0.50 mm,可满足绝大部分GNSS气象学研究的需求,且其计算参数较少,转换效率较高。 本文利用2017~2018年东南沿海地区18个GNSS站的数据,通过分析PWV与ZTD、地面气温(Ts)、地面大气压(Ps)等参数的相关性,基于多元线性拟合方法构建东南沿海地区的多因子PWV直接转换模型,得出以下结论: 1)PWV与ZTD之间的相关性最强,相关系数达到0.98;PWV与Ps、Ts之间也具有较强的相关性,相关系数分别为-0.65和0.78。 2)基于ZTD的单因子PWV模型平均bias为3.73 mm,RMS为4.66 mm;基于ZTD和Ts的双因子PWV模型平均bias为3.13 mm,RMS为3.94 mm;基于ZTD和Ps的双因子PWV模型平均bias为0.40 mm,RMS为0.50 mm;基于ZTD、Ts和Ps的多因子PWV模型平均bias为0.24 mm,RMS为0.33 mm。多因子PWV直接转换模型的精度最高,基于ZTD和Ps的双因子模型次之,这两种模型均可获得精度优于1 mm的PWV结果。 3)东南沿海地区的PWV直接转换模型不仅可应对传统PWV计算过程数据量大、效率低且易产生误差累积的问题,也可在基本地面气象数据缺失时,基于ZTD直接计算特定时段的PWV时序信息,以用于GNSS气象学研究。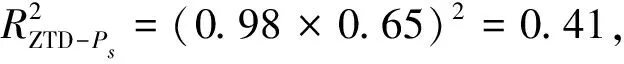
2 PWV直接转换模型的建立及精度分析
2.1 建模方法
2.2 精度检验
3 结 语
——以多重共线性内容为例

