基于混合格式Richards方程的非均质土体渗流模拟
何玲丽 ,田东方
(1.水利与环境国家级实验教学示范中心,湖北 宜昌 443002; 2.三峡大学 水利与环境学院,湖北 宜昌 443002)
许多岩土工程问题涉及到非饱和渗流过程,例如边坡工程中的降雨入渗[1],环境工程中地下水污染物运移等。非饱和渗流过程可由Richards方程描述[2],该方程有3种基本格式:体积含水率格式(θ-form)、压力水头格式(h-form)和混合格式(mixed form)[3-4]。在数值模拟求解Richards方程时,体积含水率格式的优点是允许使用较大时间步长且具有质量守恒特性。但由于体积含水率在材料界面不连续,一般来说该格式适用于均质土体;经过Hills等[5-7]的发展,也可用于模拟非均质土体,但只适用于非饱和渗流模拟。压力水头格式适用于饱和-非饱和渗流模拟,但在模拟干土入渗时,该格式需要采用非常小的时间步长和细密网格,才能保证质量守恒。为此,Phoon等[8-9]提出使用混合格式,同时在迭代过程中将本次迭代的含水率在上次迭代的含水率处按泰勒级数展开为压力水头形式。
由于混合格式具有质量守恒特性,因而也被用于主变量转换法(primary switching technique),目的在于结合体积含水率格式和压力水头格式的优点,即模拟时对非饱和区域采用体积含水率格式,饱和区域采用压力水头格式[10]。随后,Hao等[11-12]提出对非饱和区域采用混合格式,而饱和区域采用压力水头格式的方法。He等[13]进一步指出,混合格式同样适用于饱和-非饱和渗流模拟。
综上所述,基于混合格式的数值模拟具有质量守恒特性且能模拟饱和-非饱和渗流的优点。但是采用有限元模拟时,该格式需知节点处的体积含水率,由于体积含水率在材料分界面不连续,使得模拟非均质土体渗流时存在一定困难。目前,针对混合格式模拟时体积含水率不连续问题的详细探讨鲜有发现。因此,本研究目的在于建立一种基于混合格式Richards方程的非均质土体饱和-非饱和渗流有限元模拟方法。
1 基本理论
1.1 非饱和渗流控制方程
以忽略源汇项的二维各向同性问题为例,混合格式Richards方程[1]为:

式中:θ为体积含水率[L-1];t为时间[T];H为总水头[L],H=y+h,y为位置水头[L],h为压力水头[L];K=KrKs为渗透系数[L/T],Kr为相对渗透系数,Ks为饱和渗透系数[L/T];x、y为坐标[L],y轴竖直向上为正。L和T分别表示长度、时间量纲,下同。
在求解域 Ω 内初始条件为:

边界条件为,在 Γh上为本质边界条件:

在 Γq上为自然边界条件:

式中:H0、、¯为 已知函数;nx、ny分别为 Γq外法线单位向量在x、y轴的分量。
1.2 Gardner模型
Richards方程的求解还需补充 θ与h的关系,即土水特征曲线(SWCC),以及渗透性函数Kr的表达式,本文采用Gardner模型[14]:
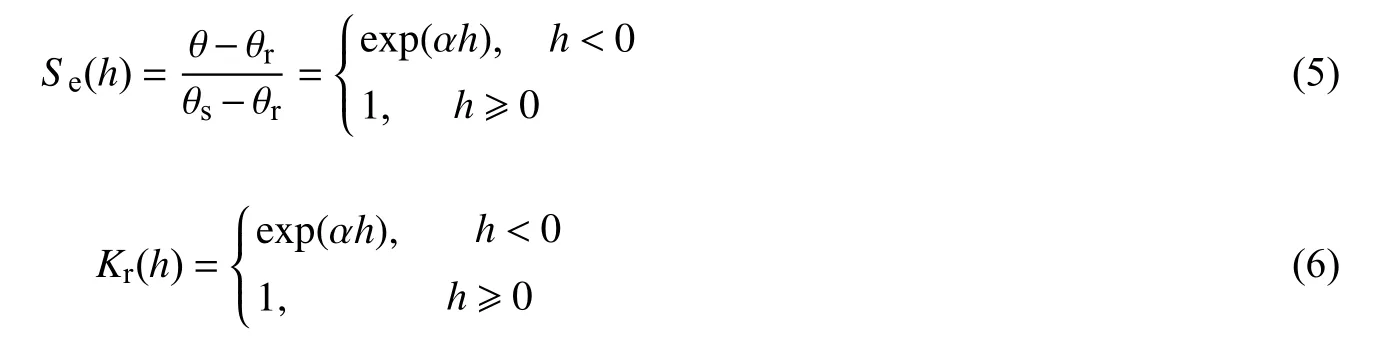
式中:Se为有效饱和度;θr为残余体积含水率; θs为饱和体积含水率;α为拟合参数[L-1]。
2 混合格式Richards方程有限元模型
2.1 渗流控制方程的变分提法
用H+和H-表示在材料分界面 Γm两侧不同材料区域内的总水头函数(图1),则当 (x,y)∈Γm时,保证总水头函数在材料分界面上连续的条件可写为:

图1 离散后的单元及节点示意Fig.1 Sketch of elements and nodes

设非饱和渗流问题的泛函记为 π,并假定其满足本质边界条件(式(3)),则:

式中:c= ∂θ/∂h,为容水度[L-1];λ为拉格朗日乘子,是坐标的函数。
可证明泛函的变分 δπ =0与式(1)等价,且包含自然边界条件(式(4))和连续性条件(式(7))。证明如下:假设求解域 Ω 包含若干种不同材料区域,其中一个区域用 Ωk表示,的本质边界;表示 Ωk的自然边界;表示 Ωk的材料分界面;则的变分为:
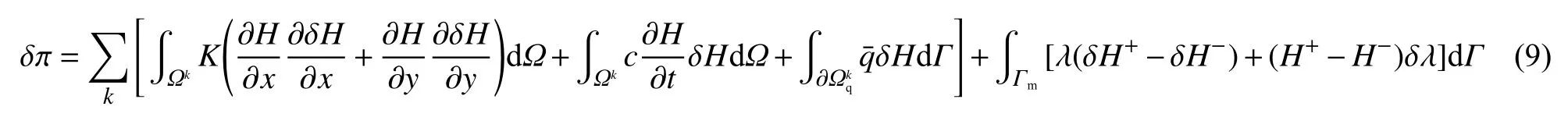
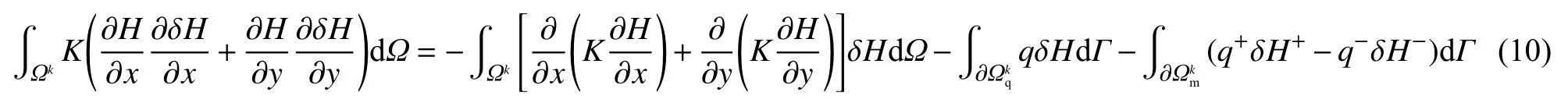
式(10)中,q按式(4)计算,q+和q-按下式计算:

式中:上标“+”和“-”表示相应物理量属于两种不同材料时在边界的取值。
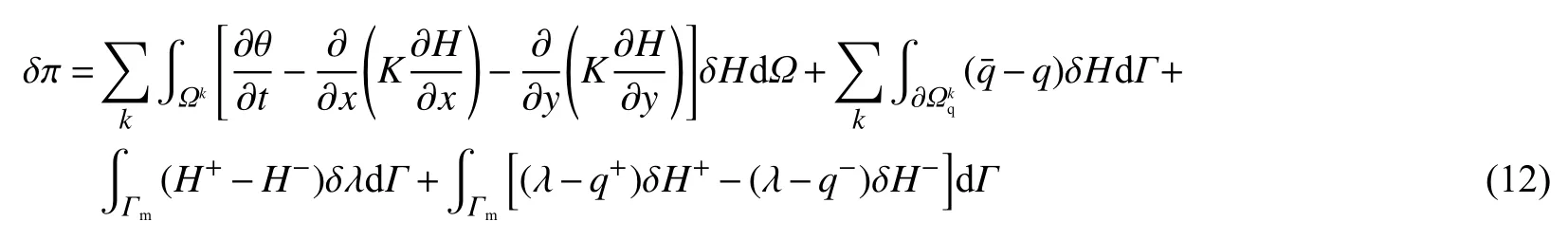
若 δπ =0,则根据式(12)等号右边的第1项可得Richards控制方程(式(1));第2项可得控制方程需要的自然边界条件(式(4));第3项可得总水头函数连续性条件(式(7));第4项可得 λ的物理意义为边界流量。
2.2 求解域离散及近似函数
本文选用四边形四节点单元,渗流和拉格朗日乘子两套网格的拓扑信息确定如下:
渗流网格为适应体积含水率在材料分界面的不连续,赋予材料分界面上的渗流节点两个编号(指整体编号),如图1中的点p1,在单元中编号为,而在单元中编号为。用数组Lφ记录单元的节点编号,例如
拉格朗日乘子网格中的节点坐标同渗流节点(位于材料分界面的节点),但从1开始独立编号(指整体编号),如图1中点p1和p2,编号分别为、。用Lλ记录单元节点的整体编号,如Lλ(kλ,1)=。用数组L记录单元节点对应的渗流节点整体编号,例如

式中:Nr为四边形四节点单元形函数;Hr为单元节点处总水头值;r=1,2,3,4。
总水头函数在求解域 Ω 的近似为:


式中:wr为一维两节点单元形函数; λr为单元节点处拉格朗日乘子值;r=1,2。
拉格朗日乘子函数在求解域 Γm的近似为:

2.3 有限元离散格式
将式(14)和(16)代入式(8),并令 δπ =0,可得式(1)的有限元离散格式,写成矩阵形式:


式(17) 对时间采用向后差分离散后可得:
当前,自然资源确权登记就是将相对完整的生态功能区域作为一个自然资源登记单元,自然资源统一确权登记将各类自然资源的质量、数量和保护要求全面摸清,并通过登记的法律手段予以公示明确,落实到每一个产权人或者使用权人,有助于充分掌握自然资源家底,并根据自然资源容量和承载力进行分类开发和保护,做到自然资源分类施策。

式中:m为 时间步数;k为第m+1时步内的迭代次数; Δt为时间步长。
为保证求解过程中质量守恒,按Celia等[2]的建议,将节点处体积含水率 θ按下式展开:
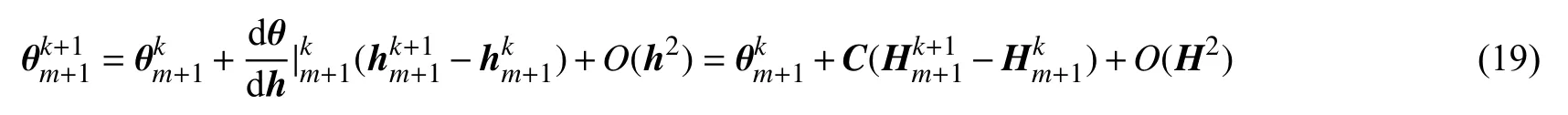
式中:C为对角矩阵,c(i,i)= ∂θi/∂hi,i为节点号。
略去式(19)中的高阶无穷小,将其代入式(18)得:

式(20)即为混合格式Richards方程的有限元求解模型,可用于模拟非均质土体饱和-非饱和渗流。该模型将拉格朗日乘子作为未知量与节点总水头一起求解,使计算量有所增加;线性方程组的系数矩阵对称但不具备正定性。根据该式编制Matlab计算程序,实现了非饱和渗流数值模拟。
3 模型验证
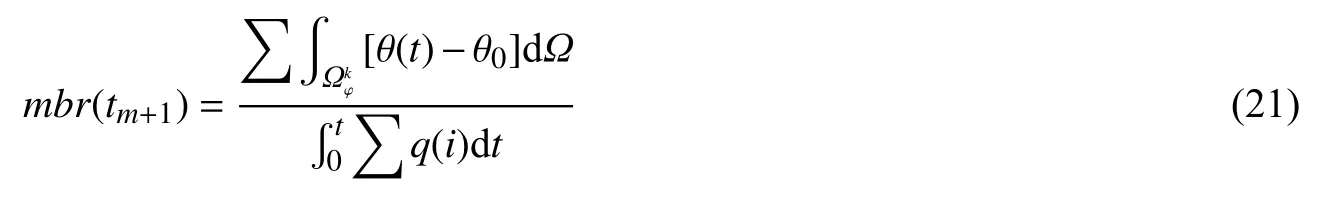
第m+1时步的q按下式确定[8]:

3.1 与Srivastava等[15]的解析解对比
计算模型为一维两层土土柱,层厚100 cm;计算域为y∈[-100,100],单位cm。y=-100 cm处为地下水位,即h= 0;顶部y=100 cm处为入渗边界,以入渗率为q0的稳定状态为初始条件,当t> 0时入渗率变为q。土水特征曲线和渗透性函数按式(5)和(6)确定,参数见图2。
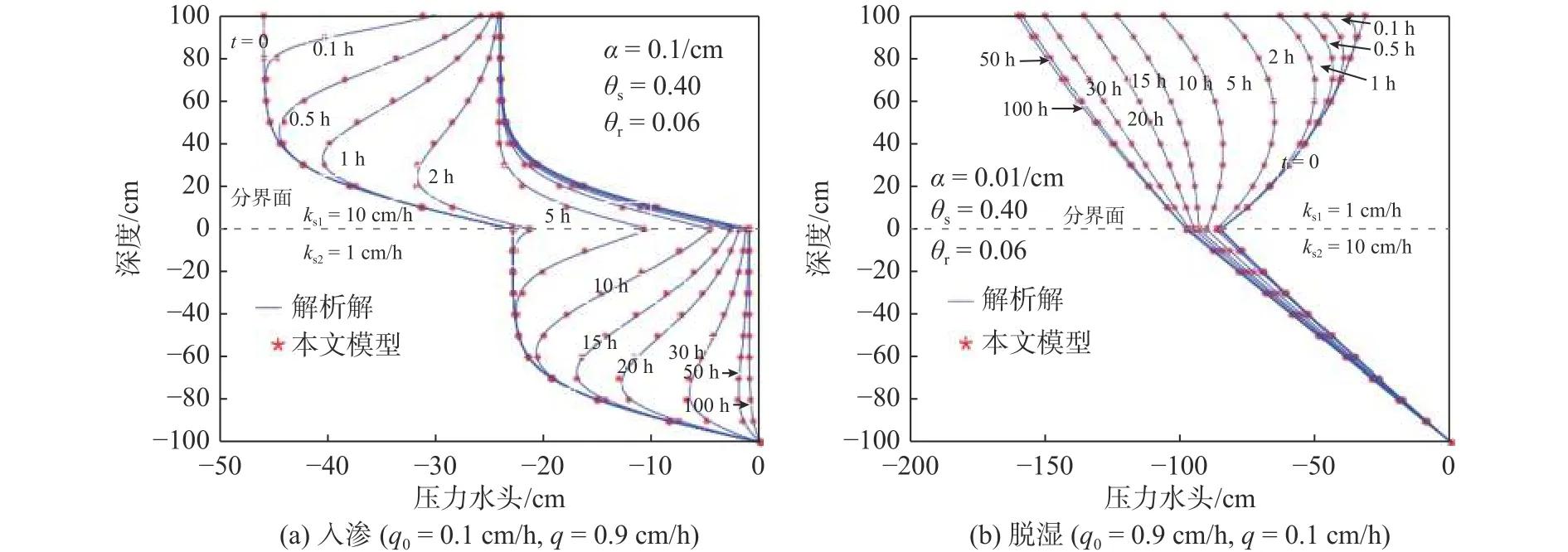
图2 入渗与脱湿时压力水头模拟与解析解的对比Fig.2 Comparison of analytical and simulated solutions
模拟时计算网格 Δy=10 cm,允许误差10-4cm,时间步长 Δt=0.01 h,时长100 h。不同时刻压力水头沿y轴分布的模拟结果与解析解对比见图2。
从图2可见本文模型结果与解析解基本吻合。不同时刻质量守恒比率(rmb)见图3,可见质量守恒比率rmb几乎为1,这表明本文模型所得结果满足质量守恒。
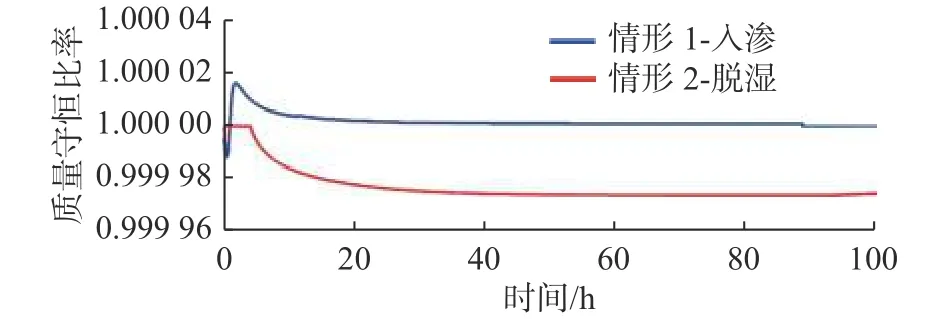
图3 质量守恒比率随时间变化Fig.3 Evolution of mass balance ratio
3.2 与Shahrokhabadi等[4]的数值解对比
计算模型如图4所示,坐标单位m。底部对应地下水位,即h= 0;顶部左侧为入渗边界,入渗率q=0.7 m/d,其余为不透水边界。初始条件为H0=0。土水特征曲线和渗透性函数按式(5)和(6)确定,计算区域坐标点(坐标单位m)和计算参数见图4。模拟时计算网格 Δx=0.25 m, Δy=0.15 m,允许误差10-4m,时间步长 Δt=0.001 d,模拟时长 2 d。

图4 二维层状土计算模型(单位:m)Fig.4 Model of layered soil for simulation(unit: m)
选取在0.1 d和2.0 d时刻,对比本文与文献所得压力水头等值线(见图5),从图5可知,两种方法所得结果差别很小,这表明了本文模型的正确性。
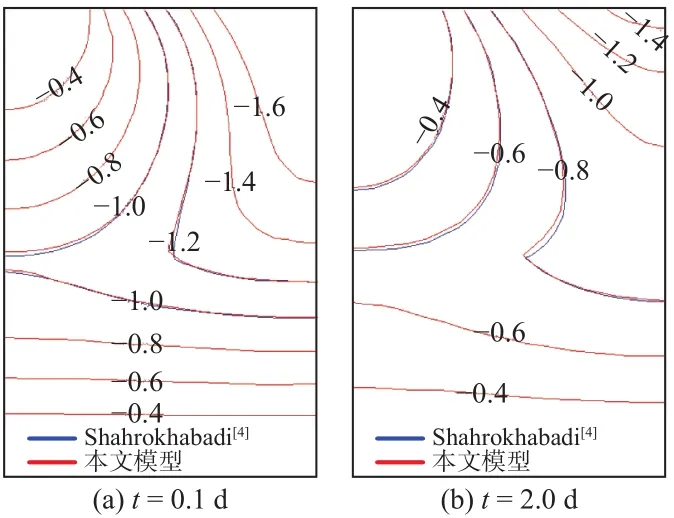
图5 压力水头等值线对比(单位:m)Fig.5 Comparisons of pressure head contours (unit: m)
质量守恒比率与时间关系见图6,可见质量守恒比率rmb几乎等于1,这表明本文模型所得结果满足质量守恒。

图6 质量守恒比率随时间变化Fig.6 Evolution of mass balance ratio
4 结 语
对材料分界面的节点赋予两个编号,将分界面节点处的体积含水率根据不同材料按压力水头泰勒展开;应用拉格朗日乘子法施加总水头函数在材料分界面的连续条件,从而建立一种基于混合格式Richards方程的非均质土体饱和-非饱和渗流有限元数值模型。应用所建模型,开展一维层状土入渗和脱湿过程模拟以及二维层状土入渗过程模拟,将所得结果与一维解析解、二维他人文献结果进行对比,得出本文模型可用于非均质土体渗流模拟。质量守恒验证表明所建模型满足质量守恒条件。

