台风灾害下配电网弹性提升的二阶段优化方法

陈星宇，钱瞳，唐文虎，张文浩，李泽蓬，连祥龙

(华南理工大学 电力学院，广东 广州 510641)

近年来，随着我国配电网的不断扩大和完善，电力的稳定供应对国家经济活动的有序开展有着越来越重大的意义。配电网结构复杂、运行环境薄弱的特点以及极端气象灾害的频发，给配电网带来了巨大挑战[1]。这些小概率、高风险灾害不仅会在短时间内造成大量设备损坏，还会增大系统恢复的难度，进而导致大面积、长时间停电事故的发生[2]，例如2017年广东台风“天鸽”[3]、2019年浙江台风“利马奇”[4]和2021年美国德州寒潮[5]，都给当地造成了巨大的经济损失。因此，“弹性”一词被电力领域所关注，旨在强化配电网感知力和协同力，进而提升其在面对极端灾害时的抵御力和恢复力[6-8]。

配电网在极端气象灾害下的受灾过程分为灾前、灾中、灾后3个阶段，分别反映其在灾害到来前的预防能力(鲁棒性)、到来时的应对能力(智慧性)和恢复时的响应能力(恢复性)[9]。灾前主要通过降低故障率来提升弹性，文献[10-11]对配电网进行脆弱性评估并有针对性地加固以提升弹性；文献[12]进一步考虑植被管理。灾中方面，文献[13]针对电网状态进行马尔科夫建模，并使用动态规划算法进行调度决策。灾后主要通过配电网重构、应急车和维修策略优化等来提升弹性，文献[14-16]提出分布式电源与联络线路结合的协同策略，文献[15]还考虑了配电网的通信情况；文献[17]考虑固定式和移动式分布式电源，通过合理安排移动式电源的位置来提升弹性。但上述文献采用的分布式电源容量都是固定不变的。文献[18-19]考虑了灾后维修队的调度情况、协同优化应急和维修资源，以最大化供电恢复。上述研究虽能在不同阶段有效提升弹性，但只局限于某一阶段，缺少不同阶段的协同优化研究。

文献[20]通过灾前确定移动储能车的位置和灾后的协同调度，减少了配电网停电总量和储能车的路程时间。文献[21]考虑柴油发电机、储能电池和电动汽车的预分配，提升了配电网在灾后对关键负荷的供电能力。文献[22]通过灾前对维修站和充电站位置的预定位和灾后恢复调度维修车和充电车，以此协同提升弹性。但上述文献均从灾前、灾后2个阶段出发，未考虑灾中的配电网响应情况，且由于灾中配电网状态变化迅速、不确定性大、时效性要求高，无法实现对应急资源的实时交通调度，采用容量不变的应急资源对系统的弹性提升效果有限。

在此背景下，本文提出一种台风灾害下考虑配电网运行成本、负荷重要度、联络线路和灵活应急发电资源的二阶段灾前-灾时弹性提升策略。基于台风预测数据和线路故障模型，在灾前预分配应急车辆的位置及其装载不同容量应急发电机的数量；在灾时协同调度联络线路的开合和应急发电车的出力，以实现配电网整体弹性提升。将上述规划和运行问题转化为混合整数线性规划(mixed integer linear programming， MILP)，并基于MATLAB-YALMIP平台调用商业求解器GUROBI进行求解。最后在IEEE 33节点和141节点配电系统中进行测试，验证所提策略的有效性。

1 配电网弹性评估指标和提升方法

1.1 弹性评估指标

设定台风开始过境时刻t0、离境时刻t3和配电网所有故障线路完成检修时刻t6，本文将灾害下配电网的状态变化过程分为灾前准备Tpre、灾中抵御Tdur、灾后恢复Trec和灾后学习Tstu这4个阶段。图1所示为台风期间配电网的状态曲线。图1中：P0为系统总加权负荷需求量，P1为加权失负荷量最大时的加权负荷总量；t1为配电网开始切负荷的时刻，t2为最大加权失负荷量对应的时刻，t4为配电网负荷开始恢复时刻，t5为配电网恢复所有负荷供电的时刻。

图1 台风期间配电网的状态曲线

为准确评估配电网弹性，本文以配电网加权负荷为纵坐标(节点失负荷量与其重要度的乘积)，根据状态曲线分别计算加权失负荷速率、最大加权失负荷率、相对负荷恢复速率和综合面积弹性指标，以量化配电网弹性能力。前3项指标分别对应抵御、降负荷运行和恢复阶段配电网的弹性表现，最后1项指标反映配电网受灾全过程的综合弹性表现。

1.1.1 加权失负荷速率

加权失负荷速率Slos指配电网从正常运行变为降负荷运行状态的平均速度，与配电网的抵御能力有关：

(1)

1.1.2 最大加权失负荷率

最大加权失负荷率Rrate反映配电网受灾的最严重程度，与配电网的吸收能力有关：

(2)

1.1.3 相对负荷恢复速率

相对负荷恢复速率Srec是指配电网在极端灾害离境后，迅速恢复到正常负荷水平的速度，与配电网的维修资源与调度策略相关：

(3)

1.1.4 综合面积弹性指标

综合面积弹性指标Rarea采用受灾状态与正常状态曲线相比的形式计算，能直观反映配电网的整体弹性表现：

(4)

1.2 灾前-灾时二阶段弹性提升方法

随着配电网的发展，智能设备的运用也变得广泛。联络线路和应急发电资源能提升配电网灵活性和抵御大范围故障的能力[23-24]。为提升配电网灾前前瞻能力和灾时应变能力，本文以装有远控开关的联络线路和应急发电车为基础，将提升配电网弹性的策略定义为二阶段问题：灾前应急发电资源预分配和灾时配网重构与应急发电车协同调度问题，其中灾时包括灾中抵御和灾后恢复2个阶段。图2所示为二阶段配电网弹性提升方法流程。

图2 二阶段配电网弹性提升方法流程

图2中灾前预分配策略主要包括3个部分：获取台风预测信息并对配电网进行网格化划分；利用台风风场模型和线路故障模型分别估计过境时配电网区域内风速的大小和各线路档距在不同时刻的故障概率；应用该结果进行灾前应急车容量和位置的预分配。灾时的实时调度策略主要包括3部分：配电网的状态感知设备实时获取线路故障状态和修复状态；应急车发电车出力和配电网线路重构方案制订；灾后恢复阶段维修队对故障线路的维修。

2 灾前应急发电资源预分配策略

2.1 台风灾害致灾模型

工程应用中，通常将台风的影响量化为致灾因子进行分析，如台风风速、风向等。改进型Rankine台风风场模型是以同心圆分布为基础，将台风影响量化为风速大小，其计算式为[25]：

(5)

式中：vt为t时刻实际风速大小；vmax为台风最大风速；r为距离台风中心的距离；Rmw为台风最大风速半径；X为风场分布参数，一般取0.5。

2.2 配电网线路故障模型

首先进行网格化，将每条线路在经度和纬度上划分为平均档距边长的网格。由于网格区域相对台风足够小，可以假设每个网格的地理位置和台风灾害强度一致。配电网元件的故障概率可用脆弱性曲线来描述[26]，以台风为例，t时刻线路n-n′第k个网格元件发生故障的概率

(6)

式中vdes为元件设计最大抵御风速。

每个网格元件通过串联形式构成线路，当某条线路任一元件发生故障，则认为该线路故障，因此t时刻线路n-n′的故障概率

(7)

式中Ωn-n′为线路n-n′的网格集。

2.3 应急发电车容量和位置分配

应急资源主要包括应急车和应急发电机，应急车通过装载一定数量的发电机到负荷节点，实现灾时配电网的电力供应。由于不同容量的应急发电机和车辆数量均有限，且为保证安全性，灾时车辆不进行调度，需在灾前合理预分配应急资源，以最大化配电网弹性。本节利用台风预测数据，通过蒙特卡洛抽样方法，选取一定数量故障场景进行最优预分配策略求解。决策变量包括应急车的位置和各自装载不同容量发电机的数量。

2.3.1 灾前目标函数

灾前目标函数主要考虑应急车配置成本和灾时运行成本，通过抽样模拟台风对线路的时序影响，求得配电网整体成本最小的方案。灾前分配策略的目标函数为

(8)

应急车配置成本

(9)

2.3.2 应急车位置约束条件

为保证应急车接入配电网，各节点最多只配置1辆应急车，应急车数量总约束为

(10)

只有配置应急车的节点才能配置应急发电机，需满足条件

(11)

式(10)、(11)中：NV,set为应急车总数；M为相对较大常量，本文中该值取应急发电机总容量。

2.3.3 应急车容量约束条件

不同型号应急发电机的容量是不同的，需将各容量的发电机分配给应急车。应急车有功和无功容量与装载应急发电机的关系式如下：

(12)

∀n∈ΩN；

(13)

各容量应急发电机的数量约束为

(14)

应急车装载发电机的数量约束为

(15)

3 灾时配电网重构和应急发电车的协同策略

本章主要讨论灾时如何配置联络线路的开合状态和分配各节点应急发电车的出力，在满足配电网运行的约束条件下进行最优潮流求解，以达到配电网总体损失最小目标。

3.1 灾时目标函数

台风过境时，为了保证社会秩序稳定，应保证与医疗、抢修和应急处理等相关的负荷有较高的供电优先级。为了体现这类负荷的重要程度，将配电网失负荷总惩罚成本表示为线性关系，即

(16)

在此基础上，加入变电站、应急发电车和联络线路运行成本，即可得本文目标函数：

min{Ct,ω,O}=min{Ct,ω,S+Ct,ω,G+Ct,ω,L+Ct,ω,B}=

∀t∈T.

(17)

“我和果智私信了几次，就把这事敲定，钱直接打到商家的账户。我信任他”。此前，他们素未谋面，只是互粉，王文志对果智的“改革”提法有好感，果智继而钦佩他的勇气。

该目标函数有3个数量级，其中变电站运行成本数量级最小，应急发电车和联络线路运行成本其次，加权失负荷惩罚成本数量级最大。在灾害刚来临影响不大时，配网以变电站出力优先出力优先，减少发电车出力和联络线路闭合数量，实现经济效益最高。当灾害影响逐渐扩大、配电网必须削减负荷以满足安全性时，由于失负荷惩罚成本较大，通过投入联络开关和应急发电车，以优先满足负荷削减最小为首要目标，并以其余运行经济效益最高为次要目标。

3.2 线路运行状态约束条件

装设远控开关的线路为联络线路，未装设的为常闭线路。若联络线路故障，则已经闭合的线路会断开，而未闭合的线路将无法闭合。若常闭线路故障，则该线路会断开。线路运行状态约束如下：

n-n′∈Ωb,L；

(18)

n′∈Ωn,N，n-n′∈Ωs,L；

(19)

(20)

式中：γn-n′,t,ω为0-1变量，表示线路故障状态，可通过每一时刻获取的线路状态信息来确定；Ωb,L为未装设开关的常闭线路集；Ωs,L为联络线路集。

3.3 应急车出力约束条件

应急发电车可视为发电机组，需对其出力进行调整，其出力范围与灾前预分配有关。应急车的有功、无功出力和工作状态约束为：

(21)

(22)

(23)

3.4 其余电力系统运行约束条件

其余电力系统约束包括节点功率、负荷和电压约束及线路传输功率和容量约束等。一般来说，配电网只有1个变电站根节点，其余节点呈辐射状分布，线路潮流计算还需满足辐射状约束。但有研究表明在遭受极端灾害影响时，舍弃该约束可提升配电网弹性[17]。鉴于本研究背景为台风灾害，故未建立此约束，以最大化配电网弹性。

在电网中每个节点的注入功率和流出功率应该相等。式(24)和(25)分别给出每一时刻配电网中节点的有功和无功功率平衡等式约束：

(24)

(25)

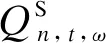
3.4.2 节点负荷削减约束

节点负荷削减约束是节点允许削减的最大负荷量，负荷有功和无功功率削减的范围分别为：

(26)

(27)

负荷有功和无功功率功角约束为

(28)

式中φn,L为节点n的负荷功率因数角。

3.4.3 节点电压约束

为了保证配电网运行电压的稳定，还需建立节点电压约束，其表达式为

Un,min≤Un,t,ω≤Un,max, ∀n∈ΩN.

(29)

式中：Un,t,ω为t时刻场景ω下节点n的电压幅值平方；Un,min和Un,max分别为节点n电压幅值平方的最小值和最大值。

3.4.4 线路传输功率约束

当线路通电时，其传输功率与两端的电压存在等式关系。考虑到线路存在连通和断开2种状态，无法直接用线性约束表示，采用大M法将该约束转化为线性约束，分别如下：

∀n∈ΩN,n′∈Ωn,N；

(30)

∀n∈ΩN,n′∈Ωn,N.

(31)

式中Rn-n′和Xn-n′分别为线路n-n′的电阻、电抗值。

3.4.5 线路容量约束

根据输电线路设计规范，各线路都有其最大传输容量，线路传输容量约束为

(32)

该约束为二阶非线性约束，可以用如下4个线性约束近似表示：

(33)

4 二阶段问题模型求解

4.1 灾前目标函数简化

2.3.1节目标函数中的配电网受灾总时间与配电网的损坏程度有关，但尚未有准确方法进行估计。其次，台风、线路故障及其所需修复时间的不确定性也会增大状态空间。目标函数的求解规模也会因受灾和恢复时间的增加及配电网规模的增大而大幅增大，造成维数灾问题，需简化求解。

在受到极端灾害影响时，由于配电网范围较小，台风过境时间较短，故障线路修复完成的时刻远晚于台风离境时刻，进而导致系统处于降负荷运行的时间相对较长[27]。为了减小灾前预分配的求解时间，本节将目标函数式(8)中配电网受灾全阶段的最优问题简化为被破坏最严重时刻，即台风离境时刻的最优问题，如下：

(34)

式(34)中第1个min部分为抽样场景总成本最小，max部分代表整个受灾过程中影响最大的时刻，以t2时刻进行计算，第2个min部分为灾时影响最大时刻的运行成本最小。各线路在最严重时刻的抽样故障概率

(35)

本研究主要针对提高配电网遭受破坏时的弹性，为保证其有一定的抵御能力，可忽略抽样所得的无故障场景，以进一步加快求解速度。

(36)

4.2 模型求解

经过简化，本文建立的二阶段配电网弹性提升方法模型的完整描述如下：

灾前：

(37)

灾时：

(38)

式(37)、(38)均为MILP问题，相比linprog工具包，YALMIP具有语法简单、方便易用的特点；相较CPLEX求解器，商业求解器GUROBI则在求解该类型大规模问题中有明显优势。故本研究基于MATLAB-YALMIP平台开发上述二阶段问题模型程序，并调用GUROBI求解器进行求解。

5 算例分析

5.1 测试平台

为验证该方法的效果，基于MATLAB软件实现对配电网受灾的模拟[28]。首先根据配电网的地理位置，将其划分成边长为平均档距的网格；然后利用式(5)计算台风致灾因子强度，并采用式(6)、(7)计算线路故障概率；接着采用蒙特卡洛方法对线路状态抽样，模拟故障场景。在每个调度时刻对线路的每个网格随机生成1个0～1之间的数，若该数小于故障概率，则认为该网格的线路故障，并通过该故障点的台风强度和位置，估算所需检修时间，再对灾后恢复进行模拟。

灾中抵御阶段线路状态的场景模拟生成式为

(39)

式中Kn-n′,t,ω为t时刻场景ω生成的0～1之间随机数。

该场景模拟主要采用蒙特卡洛法，在每个时刻对每条线路生成1个0～1之间的随机数，若该随机数大于线路该时刻的故障概率则不发生故障，反之则发生故障。同时，对于上一时刻已经故障的线路，因为在灾中抵御阶段无法对线路进行修复，所以在下一时刻其仍处于故障状态。

灾后恢复阶段线路状态的模拟生成式为

(40)

如果修复时间大于所需修复时间，则线路恢复正常。同理，对于上一时刻没有故障的线路来说，因为在灾后恢复阶段台风灾害已过镜，在下一时刻，该线路不会受台风灾害影响而发生故障。

同时，本文假设在整个受灾期间，线路故障都是由台风导致的断线和倒塔造成的；而对于其他故障，例如短路故障、因操作不当造成的线路故障等，因为其发生概率相对较小，故忽略不计。维修所需时间主要考虑灾害强度、故障线路位置和维修资源有限需等待的时间之和[28]，即

(41)

最后进行200次独立抽样，记录每个时刻系统负荷供电情况，并计算系统平均状态曲线。

5.2 IEEE 33节点测试系统结果

本节基于改进IEEE 33节点配电网系统进行测试[29]，系统单线图和台风路径如图3所示，参数设置如下。

图3 IEEE 33节点测试系统和测试台风路径

a)采用2016年第4号台风“妮妲”数据进行仿真分析，台风中心每6 min移动1次，最大风速33 m/s，移动速度为15 km/h。

b)该测试系统有32条常闭线路和5条联络线路(8-21、9-15、12-22、18-33、25-29)，线路设计的抗风标准均为28 m/s。该系统有1个变电站节点和32个负荷节点，假设节点8、21、31、33为二级关键负荷节点，其节点重要度均设置为3，其余节点重要度均设置为1，总有功负荷为3.715 MW，总加权负荷为4.715 MW。

c)检修资源站位于节点28处，灾前应急车的空车调度单位成本为2美元/km，与装载量有关的容量单位调度为2美元/(km·MW)。

d)共有2种容量分别为0.1 MW和0.2 MW的应急发电机，各4台。共有4辆应急车，每台车的装载上限均为6台发电机。

e)配电网调度周期为6 min，变电站运行成本为10美元/MW，联络线路运行成本均为每调度周期50美元，应急发电车运行成本为100美元/MW，普通和关键负荷节点的惩罚成本分别为1 000美元/MW和3 000美元/MW[25]。

为验证本文所提方法的有效性，针对配电网是否存在灾前资源分配、灾时配电网重构和应急发电车，本文设置6种不同测试场景，见表1。

表1 不同测试场景下的弹性提升策略

5.2.1 灾前应急发电资源分配结果分析

基于假设条件，场景S2和S4的灾前应急发电资源默认的分配结果(各重要负荷节点均分应急资源)，以及场景S3和S5的最优分配结果见表2。

表2 IEEE 33节点系统不同测试场景的分配结果

场景S5与其他场景相比，急车配置成本和灾时总成本均最小。以场景S5为例进行具体分析，借助灾前预测可知，节点8和31有较大可能成为孤岛节点，因此将过多资源分配在这2处是非必要的，只需在这2处预设满足该节点的最小容量，而选择将更多的容量分配到节点10处。因为在灾害最严重时，4条配电馈线都很可能失去与变电站的连接，通过联络线路12-22闭合，能够恢复大量负供电，且该片区内节点10距离资源站最近。与之对应的为场景S3的结果，由于无法进行配电网重构，且线路20-21有断线风险，节点22处只能预设恰好满足节点21和22总需求的最小容量。除此之外，由于线路29-30、30-31、31-32存在断线风险，但没有联络线路18-33，该场景没有在节点32处预设应急车，舍弃了对节点32和节点33的供电，而预设在节点10处，目的是恢复更多供电，避免资源浪费。由成本结果可知，起决定作用的是受灾阶段的运行成本。本文所提二阶段方法既能减少运行成本，又能兼顾预分配经济成本，初步验证了一阶段分配的有效性。

5.2.2 灾时配电网弹性提升结果分析

为准确评估台风对配电网的影响，蒙特卡洛抽样得到平均状态曲线，如图4所示。

图4 IEEE 33节点系统蒙特卡洛配电网平均状态曲线

计算各场景弹性指标，结果见表3。综合面积弹性指标方面：①采用本文所提二阶段策略的场景S5比不采取任何措施的S0提升56.58%，比只采取灾时措施没有灾前预分配的S4提升1.78%；②只采用应急车策略的2种方案中，有灾前分配的S3比没有的S2提升0.85%；③单独采用配电网重构的S1和应急车的S2分别比不采取任何措施的S0提升12.38%和47.11%。

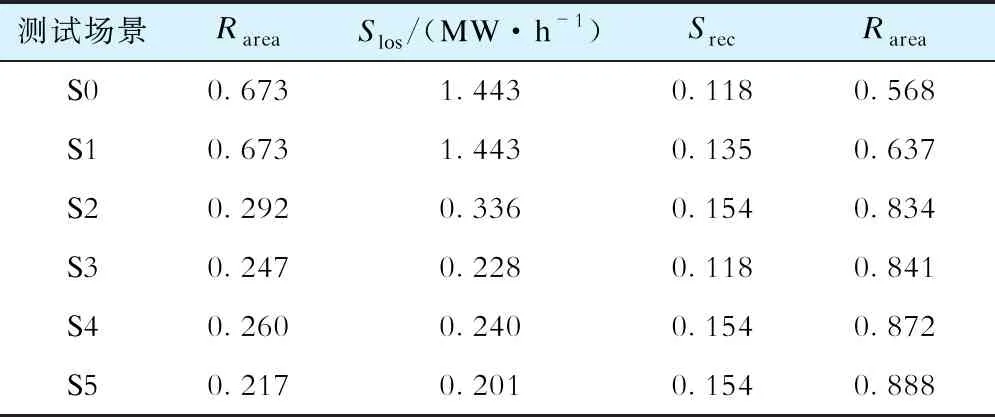
表3 IEEE 33节点系统不同测试场景下的弹性指标结果

其他指标方面，场景S5能显著降低配电网最大失负荷率和加权失负荷速度，相比S0分别下降67.76%和86.07%，相比S4分别下降16.54%和16.25%。场景S5也能提升配电网相对负荷恢复速率，相比S0提升30.51%。该结果说明本文所提策略在配电网抵御阶段、降负荷运行阶段和恢复阶段均能有效提升配电网弹性。

取某一模拟结果分析(故障事件和策略动作见附录A表A1)，状态曲线如图5所示。台风过境时刻t0=0.4 h，离境时刻t3=5.3 h。灾害离境时，各场景配电网拓扑结构如附录A图A1所示。

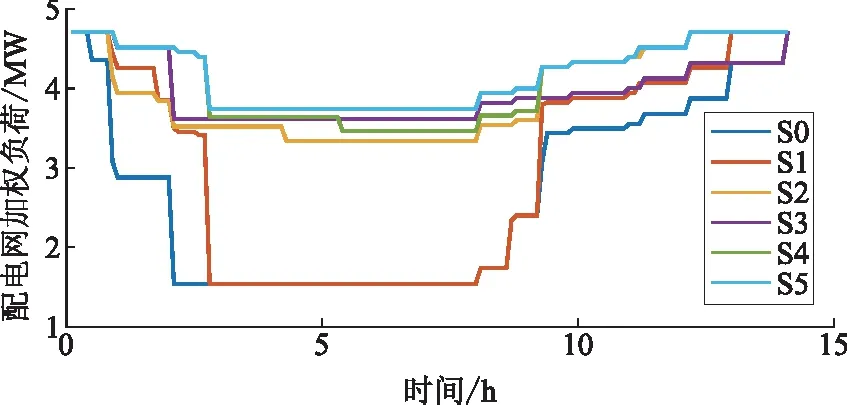
图5 IEEE 33节点系统某一蒙特卡洛仿真中配电网状态曲线

对于场景S5，联络线路12-22闭合，节点21的应急车实现对节点9—18的供应，节点8、31和33处的应急车实现对所处节点的负荷供应，由于节点33处预设的容量恰能满足节点32和33的负荷总需求，联络线路18-33无需闭合，降低总成本。

场景S4为利用节点33的冗余发电资源，线路18-33需闭合。场景S3由于没联络线路，只能舍弃重要负荷节点33，将更多容量预设在负荷集中片区，导致整体弹性下降。场景S2也因没有配电网重构策略，造成资源冗余浪费，使系统弹性下降。在灾害离境时刻大规模线路出现故障，导致各馈线都与变电站失去连接，场景S1无法通过联络线路来提升弹性，但在灾时发展阶段配电网重构相比场景S0仍能提升配电网的弹性。

5.2.3 灾时配电网成本和应急车出力分析

配电网各运行成本平均值如图6所示，各场景总平均运行成本总体与综合弹性指标呈负相关关系，且各项成本的数量级关系也与3.1节中目标函数设立的3个数量级一致。为进一步说明所提方法的有效性，图7和图8分别为场景S5运行成本和各节点出力变化。

图6 IEEE 33节点系统各项运行成本的平均值

从图7可看出：灾害未过境时，所有运行成本都来自变电站；灾害发展初期，可以通过联络线路和应急车的配合，避免负荷惩罚成本出现；当灾害扩大到无法避免削减负荷时，尽可能保证加权负荷削减最少；当灾害离境线路开始修复时，负荷惩罚成本最先减小，并随着线路被修复，变电站运行成本逐渐上升。由图8也可得到相似结论，在整个受灾过程中，配电网总输出功率先减小后恢复正常。台风开始过境后，变电站的有功输出先不变，后逐渐减小，转而由各节点应急发电车承担一部分出力；随着线路修复，又重新恢复到由变电站向配电网所有负荷供电的情况。结合图7、图8，变电站初始出力不变的原因是：虽有一定数量线路故障，但可通过联络线路闭合实现重构，将变电站出力保持在正常水平，与目标函数设定相符。

图7 IEEE 33节点系统场景S5中各项运行成本的变化

图8 IEEE 33节点系统场景S5中各节点出力的变化

5.2.4 应急发电资源配置灵活性分析

本节针对应急发电车资源灵活性进行分析，通过保持发电车数量和发电机总容量不变、改变应急发电机的种类和数量，分析资源配置灵活性对方法的影响，结果见附录A表A2。与场景S5相比：①场景S6只有0.2 MW发电机，其Ct,ω,O和Rarea值均相等，分别表示配电网运行成本和整体弹性基本一致，但灾前应急车配置成本CA较大；②场景S7和场景S8均配置了较大容量发电机，其CA值较小，系统整体弹性降低；③场景S9也配置了较大容量发电机，CA值也有所减小且整体弹性并没下降，但是由于资源集中，造成配电网运行成本增大，主要表现在联络线路闭合数量增多，以维持更大区域供电。为充分发挥发电机的灵活性因此，如何合理利用应急车装载不同容量发电机的灵活性来最大化配电网弹性，是本研究未来拓展内容之一。

5.2.5 应急车总容量和数量灵敏度分析

本节就所提模型的灵敏度进行分析，通过改变应急车数量和总容量，求得不同最优预分配策略，并比较其在相同灾害条件下配电网的弹性。以IEEE 33节点系统为例，结果如图9所示。

图9 配电网弹性与应急车数量和总容量的关系

随着应急车数量和总容量增大，配电网弹性整体呈上升趋势。但数量较少或总容量较小时，如果只增加任意一者，其弹性提升空间有限，很快会到达一定数值而无法继续提升。因此，为增加经济效益，应在考虑经济成本的前提下，同时兼顾增多应急车数量和提升总容量2个方面。

5.3 141节点测试系统结果

基于141节点配电网系统进行测试[30](由Matpower7.0提供)，系统单线图和台风路径如图10所示。参数设置如下：

图10 141节点测试系统和测试台风路径

a)该测试系统有140条常闭线路和8条联络线路；1个变电站节点和140个负荷节点，假设节点26、44、49、94、103、124、127、137为二级关键负荷节点，节点重要度均设置为3，其余节点均设置为1，总有功负荷为11.902 9 MW，总加权负荷为13.118 3 MW。

b)检修资源站位于节点11处。

c)共有3种容量分别为0.1 MW、0.2 MW、0.3 MW的应急发电机各8台；共有8辆应急车，每台车的装载上限均为6台发电机。

d)其余参数与IEEE 33节点测试系统相同。

5.3.1 整体弹性提升效果分析

各场景最优分配结果见附录A表A3，蒙特卡洛抽样得到的平均状态曲线如图11所示。

图11 141节点系统蒙特卡洛配电网平均状态曲线

计算各场景弹性指标，其中场景S0—S5的综合面积弹性指标值分别为0.594、0.657、0.745，0.843、0.788和0.859，对比得出结论：①采用本文策略的场景S5比不采取任何措施的S0提升44.59%，比只采取灾时措施没有灾前预分配的S4提升8.91%；②只采用应急车策略的2种方案中，有灾前分配的S3比没有的S2提升13.16%。由此可见本文提出的灾前分配策略在大规模节点系统中也能在保证经济性的同时，有效提升配电网弹性。

5.3.2 求解效率分析

为验证本文所建模型是否满足配电网调度需求，基于141节点系统，采用GUROBI和CPLEX求解器进行灾前和灾时问题的求解，并记录时间和收敛精度。采用GUROBI求解，灾前问题总共需要3 120 s，精度为0.001%，灾时1个调度周期需要3.99 s，均能满足灾前配置和灾时调度的时间需求。而采用CPLEX求解，其灾前求解时间为3 375 s，大于前者，且精度降低为0.87%，灾时求解需要4.21 s，与前者相差不大。原因是灾前模型中存在大量的整数变量且规模较大，GUROBI在这2个方面较CPLEX均有优势。

6 结束语

针对日益频发的极端气象灾害，本文提出基于二阶段优化的台风灾害下配电网弹性提升方法，算例及结果表明：①该方法能有效结合台风预测数据和线路故障概率模型，对配电网受灾情况进行模拟，并考虑灵活性在灾前合理配置应急资源位置和容量，减少了资源浪费，优化了配电网弹性提升；②与被动响应和采用单一运行策略相比，灾时联络线路和应急车出力的协同配合，可有效提升配电网弹性，在一定程度上提升配电网受灾全过程的抵御能力和恢复力；③建立混合整数线性规划问题模型，所提求解方法求解速度较快，能满足灾前和灾时的实时调度需求。

本文以台风灾害为例进行研究，所提方法具有普遍适用性，有助于电网进行灾害预警和制定灾害应对方案，为电网的应急预案设计提供参考。随着大量微源的接入，微源出力的不确定性将会给配电网调度带来全新挑战，未来研究将关注不确定因素的影响，进一步完善配电网弹性提升方法。