散斑能见度光谱法测量筒仓内颗粒流的颗粒温度

陈泉，郑泽希，李然，3，孙其诚，杨晖

（1 上海理工大学光电信息与计算机工程学院，上海 200093； 2 上海理工大学机械工程学院，上海 200093； 3 上海理工大学医疗器械与食品学院，上海 200093； 4 清华大学水沙科学与水利水电工程国家重点实验室，北京 100084）

引 言

筒仓作为常见的颗粒物料存储设备广泛应用于粮食存储、医药加工和化工生产等领域[1-4]。理想的筒仓能够在最小的占地面积上存储最多的颗粒，并且以所需的质量流率正常流出[5]。然而，在运行时，由于离散颗粒的无序运动导致了筒仓内固体颗粒无法按照质量流（mass flow）形式正常流出，引起了筒壁与颗粒之间的黏滑运动[6]，间歇性堵塞[7]以及非局域流变[8]等问题。这些问题严重影响了产品的生产质量，甚至危害筒仓的安全运行。因此，测量筒仓内颗粒的无序运动，掌握其变化规律，在筒仓设计和化工调控工程中具有重要意义。

颗粒温度（granular temperature）反映了介尺度条件下颗粒运动的无序程度[9]。Ogawa 等[10]根据微观粒子的热运动提出了颗粒温度的概念来表征颗粒系统的无序运动，用δv2～<δvδv>表示，其中δv表示无规则运动颗粒的速度波动，<>表示系综平均。颗粒温度与热力学温度相似，二者都产生压力，并且控制着颗粒系统的质量、动量和能量传播。近20年来，人们采用离散单元法（discrete element method，DEM）对筒仓内颗粒流的颗粒温度进行了大量研究，建立了介观颗粒温度与宏观颗粒流型、质量流率之间的关系模型。2007 年，Ahn[11]采用基于硬球接触模型的DEM 方法模拟不同质量流率条件下圆柱形筒仓内球形颗粒的运动，根据颗粒的矢量速度计算了筒仓内颗粒温度的轴向分布，揭示了颗粒动能的耗散率与颗粒温度值满足指数为1.5 的幂函数关系。2013 年，Tewari 等[12]采用基于颗粒动理学的DEM 方法模拟二维筒仓中球形颗粒的运动，探究堵塞前颗粒流的动力学特征。根据单位时间步长内颗粒的位移计算出筒仓内颗粒流的颗粒温度，发现了当质量流率较高时，筒仓中心区域的颗粒温度值较低；而当颗粒流接近堵塞时，颗粒温度的分布发生了明显逆转，在筒壁处的颗粒温度存在极小值。2015 年，Regele 等[13]采用基于静摩擦接触模型的DEM 方法模拟球形颗粒通过具有狭窄通道的三维筒仓，统计了单元颗粒的平移速度和旋转速度，计算了不同流态区域的颗粒温度分布。研究表明：孔口附近快速颗粒流区域内存在较低的颗粒温度值，但该位置处颗粒的旋转速度较高。扩散波光谱技术（diffusing wave spectroscopy，DWS）和散斑能见度光谱技术（speckle visibility spectroscopy，SVS）是两种能够直接测量颗粒温度的方法[14]。DWS 技术要求被测量颗粒系统的运动状态具有稳定性，以满足光子在自相关时间内的扩散传播过程；SVS 技术是在DWS技术基础上发展起来的，该测量技术的优势在于具有良好的鲁棒性，适用于筒仓内复杂颗粒流的颗粒温度测量，并且SVS 技术具有微秒级时间分辨率(由线阵CCD相机的采集帧率决定,最快可以到10 μs)和微米级空间分辨率(激光波长的1/4，约0.1 μm)。2005 年，Bandyopadhyay 等[15]根据扩散波光谱法首次提出了散斑能见度光谱技术，并应用于振动流化床的颗粒温度测量，观测到颗粒温度的测量值与系统振动频率具有相同的周期性，进而验证了该技术能够准确测量密集颗粒系统的无序运动。2010 年，Katsuragi 等[16]利用散斑能见度光谱技术测量了斜坡流中不同位置的颗粒温度分布，通过对比颗粒温度与颗粒堆积密度，发现了颗粒温度随颗粒堆积深度的变化是非线性的。2019 年，本课题组[17-19]应用该技术测量了转筒内雪崩颗粒流的颗粒温度，观察到雪崩前颗粒堆积的重排现象，发现了不规则颗粒的重排运动可以减小雪崩的持续时间。

因此，本文采用散斑能见度光谱技术，对卸料过程中筒仓内两种粒径的球形颗粒分别开展颗粒温度测量。探究了稳态流动过程中颗粒温度的分布特征以及颗粒粒径对颗粒温度的影响。最后，分析了堵塞过程中颗粒温度的变化规律。

1 实验材料和方法

为了掌握筒仓内颗粒流的复杂动力学，本文搭建了基于线阵CCD 相机的散斑能见度光谱实验装置，测量筒仓内玻璃珠在卸料过程中的颗粒温度。

1.1 颗粒材料

图1(a)是显微镜下均值粒径为0.94 mm 的玻璃珠颗粒。由于透明材料可以帮助观察颗粒床中一定堆积深度（4～6 mm）的颗粒运动，因此采用透明玻璃珠进行筒仓内颗粒流的测量实验。首先，采用标准筛网（孔径分别为0.88 和1.00 mm；孔径分别为1.40 和1.70 mm）对玻璃珠进行了两次筛分处理，获得了两种不同粒径的实验样品颗粒。然后，随机取出部分样品颗粒放置在显微镜（Olympus SZX16）的工作台上，放大25 倍后进行图像采集。最后，根据颗粒的投影面积计算颗粒的等效圆面积直径[20]。连续统计300 颗玻璃珠样品，获得实验颗粒粒径的累积分布，如图1(b)所示。表1为两种粒径玻璃珠的特征参数。表中β是颗粒堆积的下休止角[21]。

表1 实验颗粒材料的特征参数Table 1 Characteristic of granular materials used in this work

图1 实验玻璃珠的图片和颗粒粒径的累积分布(fCDF代表颗粒粒径的累积分布函数；d代表颗粒粒径)Fig.1 The image of glass beads and the cumulative particle size distributions of the glass beads

1.2 实验装置系统

图2为实验装置实物图。实验装置系统包括激光光源，凸透镜，线阵CCD 相机，滤光片，电子天平秤和矩形筒仓。光源是波长为532 nm 的半导体激光器，输出功率为100 mW，光束直径为2 mm。出射激光经凸透镜扩束得到直径为8 mm 的入射光束。当入射光与堆积颗粒发生相互作用时，产生的前向散射光被线阵CCD 相机（加拿大DALSA 的Spyder mod 3）捕获。线阵CCD 相机的像素尺寸为14 μm×14 μm，像元个数为1024 个，采样帧率设置为20 kHz。为了减弱其他光源信号对实验测量结果的影响，在线阵CCD相机的表面粘贴了532 nm的窄带滤光片。平底矩形筒仓由长方体容器和金属底座两部分组成。长方体容器采用透明有机玻璃材料加工制成，壁厚为10 mm，高度和宽度分别为240 和150 mm，前后壁面的间隙为8 mm。筒仓底座由金属铝加工制成，表面采用电镀工艺进行氧化黑处理。孔口矩形槽的宽度为8 mm，利用可调插销控制孔口矩形槽的长度D1，使得D1在[4 mm,18 mm]范围内变化。电子天平秤（SF-400）通过RS232 接口与计算机相连接，用于记录筒仓内填充颗粒的质量流率。电子秤的最大采样频率为5 Hz，重复性误差为1 g。以O点为坐标原点建立笛卡儿坐标系，其中，O点位于孔口中心的内壁上，x轴与y轴形成的平面与筒仓的前壁面平行，如图2 中矩形筒仓的正视图所示。平底矩形筒仓是关于中心垂线对称的，因此在xϵ[0,75 mm]，yϵ[0,240 mm]范围内测量颗粒温度。每个测量点的大小为直径8 mm 的圆形区域（约40 个颗粒），两个相邻测量点之间的中心距离为10 mm。测量点A位于筒仓孔口附近的快速颗粒流区域。测量点A为直径8 mm 的圆形区域，中心坐标为A(0,10 mm,0)。实验前，先利用软橡胶塞堵住孔口矩形槽，再从筒仓顶部采用均匀分散加载方式进行玻璃珠的加载。

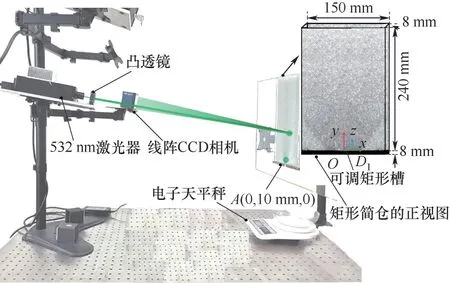
图2 实验装置实物图(D1代表筒仓孔口的长度)Fig.2 The annotated photo of the experimental setup

1.3 散斑能见度光谱法

图3为散斑能见度光谱法测量颗粒温度的原理图。假设单个光子通过离散颗粒样品时发生了N次散射，则根据扩散波光谱原理，在t时刻光子散射N次的总路径长度S为[22]

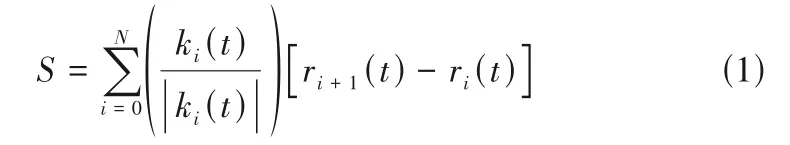
式中，ki(t)为t时刻光子经过i次散射后的波矢量；ri(t)为t时刻颗粒的空间位置坐标。同时，光子的相位可以表示为[23]

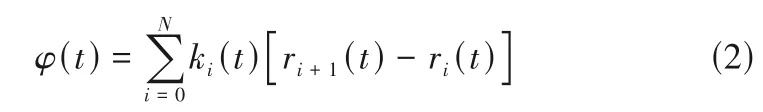
式中，φ(t)为光子相位随时间的变化函数。根据式（1）和式（2），得到散射光强E(t)的表达式为

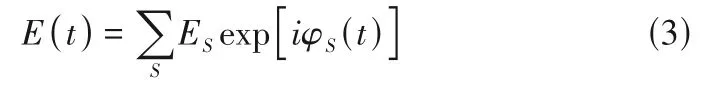
式中，ES为光程为S光子的光强幅值。

因此，散射光场的归一化自相关函数可以表示为

式中，λ为入射激光的波长；δv= <δv2>，δv2表示颗粒温度；Γ= 4πδv λ，是函数g1(t) 的衰减线宽。

根据统计光学原理，散斑图像的对比度可以用单位曝光时间内散射光强的方差σ与均值的比值来表示[24],即

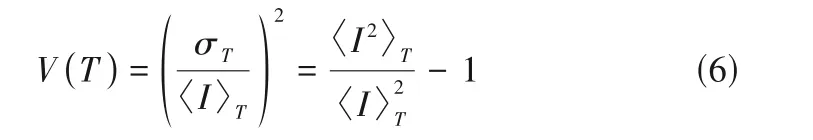
式中，T为采集相机的曝光时间。根据高斯光束的Siegert 公式，建立了散斑图像对比度与散射光场自相关函数之间的关系[25]

式中，β为测量系统的相干因子。将式（5）代入式（7），得

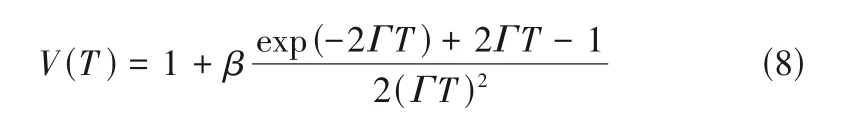
颗粒温度可以根据式（8）反演获得。注意，由于受到CCD 相机的电路噪声和测量环境的干扰，相干因子β无法被准确测量[15]。为了解决该问题，一般将2 倍和1 倍曝光时间下的散斑对比度值相除，消去系统相干因子，来获得颗粒温度δv2。另外，一般要求散斑面积的等效直径约等于10 倍颗粒粒径。

由于光子的波粒二象性，在测量区域内不同光子的传播会产生干涉现象，从而在CCD 相机上显示出“颗粒状”的散斑图像，如图3 中灰度图所示。在相同的曝光时间条件下，颗粒的运动速度越快，散斑图像的模糊程度越高，而散斑图像的对比度就越低。图3 中红色曲线是根据图3 中的散斑图像计算获得的颗粒温度变化曲线。散斑能见度光谱测量技术的重复性误差小于3%[26]。

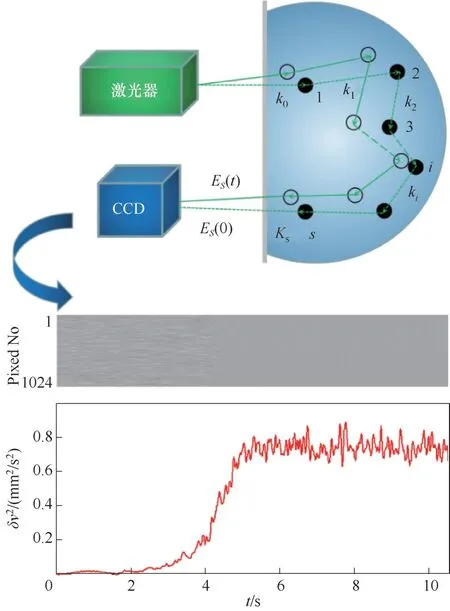
图3 散斑能见度光谱法测量颗粒温度的原理示意图[ES(t)代表光程为S的散射光子在t时刻的光强幅值；ki代表入射激光经过i次散射后的波矢量]Fig.3 Schematic diagram of measuring granular temperature by speckle visibility spectroscopy

2 实验结果与讨论

设置孔口矩形槽的长度D1=12 mm，将均值粒径为0.94 和1.55 mm 的玻璃珠加载到平底矩形筒仓内进行实验。采用散斑能见度光谱法测量卸料过程中颗粒流的颗粒温度，每个测量点重复测量10 次。由于筒仓内颗粒流的运动是关于筒仓中心轴线对称的，因此在颗粒温度测量过程中，仅测量筒仓内颗粒流的右半部分。

2.1 颗粒温度的特征

图4 为卸料过程中筒仓内测量点A的颗粒温度变化曲线。可以看出，颗粒温度曲线包含了初始瞬态流，稳态颗粒流和排空三种不同的卸料阶段。在稳态颗粒流中，颗粒温度值保持相对稳定。该结果说明了卸料过程中离散颗粒的运动在介尺度条件下具有稳定性；而在非稳态颗粒流中，由于颗粒介质之间的摩擦和非弹性碰撞具有高度的非线性[27]，导致了颗粒温度曲线存在较大的梯度变化。另外，对比卸料过程中颗粒流的三种不同阶段，稳态颗粒流的持续时间最长。因此，在接下来的研究中重点关注稳态颗粒流的颗粒温度。

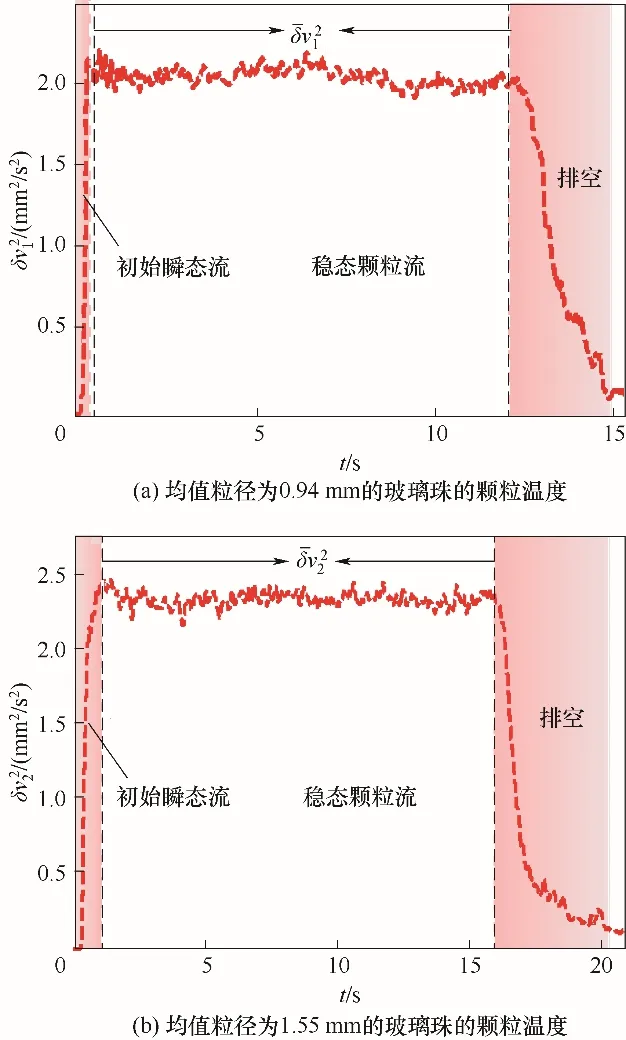
图4 筒仓内颗粒流测量点A(0,10 mm,0)的颗粒温度变化曲线(代表稳态流中粒径为0.94 mm颗粒的平均颗粒温度；代表稳态流中粒径为1.55 mm颗粒的平均颗粒温度)Fig.4 The curve of granular temperature at measuring point A(0,10 mm,0)in silo

表2 为稳态颗粒流过程中筒仓内A位置颗粒温度与质量流率的均值和方差。可以看出，10 次实验中颗粒温度的测量结果具有良好的一致性。值得注意的是，均值粒径为0.94 和1.55 mm 颗粒的质量流率分别为Q1=(33.5±0.8) g/s，Q2=(26.7±0.7) g/s；而颗粒温度为δv21=(2.02±0.01) mm2/s2，δv22=(2.35±0.02)mm2/s2。这表明了大粒径颗粒的无序运动程度更强，即大粒径颗粒在卸料过程中具有更高的能量耗散，这可能是导致其质量流率较低的直接原因。该现象揭示了介观颗粒的无序运动是控制宏观质量流率的主要因素之一。在实际应用过程中，通过在筒仓内部添加障碍物调节离散颗粒的无序运动，可以为调控宏观质量流率提供新的途径。

2.2 颗粒温度分布

图5为两种粒径颗粒在筒仓内稳态颗粒流中的颗粒温度分布。可以看出，不同粒径颗粒的颗粒温度分布具有相似性。颗粒温度的最大值出现在筒仓顶部区域，并且以“收缩”形式向下递减传播，如图5(a)和(b)所示。筒仓顶部的高颗粒温度值可能是颗粒床的雪崩运动导致的。注意，两种粒径颗粒在筒仓孔口附近均存在一个低颗粒温度区域。较低的颗粒温度值揭示了该位置处离散颗粒存在定向有序的运动，这与斑团模型中介观颗粒运动的特征相同，并且Zhang 等[28-29]在DEM 模拟实验中也观察到了类似的现象。进一步，根据Hu 等[30]的研究结果，筒仓孔口两侧的堆积颗粒可能是造成低颗粒温度的直接原因。孔口附近停滞区的颗粒堆积可以减小离散颗粒间碰撞产生的接触力，从而降低了颗粒系统的颗粒温度。这表明在实际筒仓的优化设计中，孔口两侧添加缓冲单元，可以减弱颗粒间碰撞产生的接触力，从而使得填充颗粒可以更容易排出，有利于减小筒仓的堵塞概率。

图5 稳态流动中筒仓内颗粒流的颗粒温度分布Fig.5 Granular temperature distribution of steady flow in silo

图5(b)和(e)分别为均值粒径为0.94 和1.55 mm颗粒的颗粒温度的径向分布。可以看出，两种粒径颗粒的颗粒温度的径向分布是基本相同的。在筒仓的不同高度y处，颗粒温度的变化趋势是一致的，颗粒温度值随着x的增大而减小。并且，随着y值的减小，颗粒温度为0 值的测量点逐渐增多。这表明了停滞区随着筒仓高度的降低而增多。然而，在不同的轴向位置处，颗粒温度的值随着y的增大而增大，如图5(c)和(f)所示。当测量点距离筒壁约10 mm时，颗粒温度约为0值，这表明该位置处的颗粒均处于停滞区内。

2.3 颗粒流的堵塞测量

堵塞现象在筒仓颗粒流中是随机产生的。图6 为堵塞过程中筒仓内A位置的颗粒温度变化曲线。可以看出，当t>0.06 s 时，颗粒流处于稳态流状态，颗粒温度值相对稳定，在2.02 mm2/s2上下波动。然而，当t=0.06 s 时，筒仓内颗粒流发生了堵塞现象。在0.06 s 时间内，颗粒温度值从2.02 mm2/s2减小至0。这表明了筒仓内颗粒流的堵塞现象存在一个弛豫过程。进一步，在误差小于2%的条件下，采用最小二乘法对堵塞前0.06 s 时间内的颗粒温度进行拟合处理，结果如图6 中插图所示。可以看出，堵塞过程中的颗粒温度变化满足指数函数分布。

图6 堵塞过程中均值粒径为0.94 mm颗粒在筒仓内A位置的颗粒温度变化曲线(插图为堵塞前0.06 s时间内的颗粒温度曲线；蓝色实线代表拟合曲线；Δt表示堵塞过程的弛豫时间)Fig.6 The curve of granular temperature with an average particle size of 0.94 mm at position A in silos during blockage

图7是筒仓内颗粒流堵塞过程的弛豫时间Δt随孔口矩形槽长度D1的变化曲线。可以看出，在相同孔口尺寸条件下，均值粒径为1.55 mm 颗粒的堵塞弛豫时间Δt更长。观察到D1在[4 mm, 18 mm]范围内时，两种粒径颗粒的堵塞弛豫时间Δt与孔口尺寸D1均满足正比例关系，最短弛豫时间 Δt=（0.020 ±0.002）s。该结果表明通过测量筒仓内颗粒流的介观颗粒温度信号，可以提前预测颗粒流的堵塞事件，并且随着筒仓孔口尺寸的增加，可以更早预测颗粒流的堵塞。

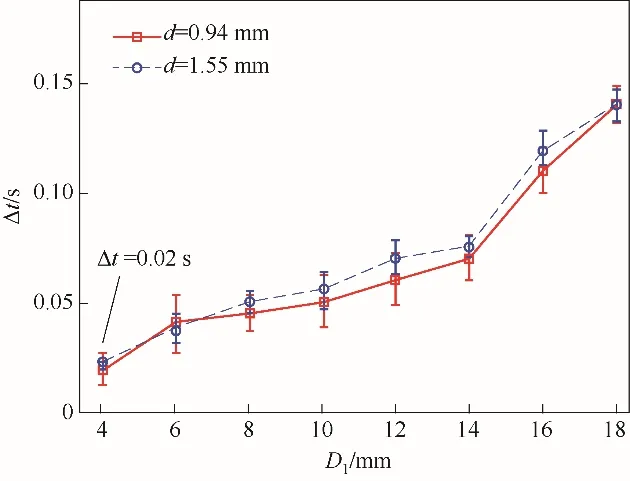
图7 筒仓内颗粒流堵塞过程的弛豫时间Δt随孔口矩形槽长度D1的变化曲线Fig.7 The curve of relaxation time of blockage changed with orifice size in silo

3 结 论

基于散斑能见度光谱技术对卸料过程中筒仓内颗粒流的颗粒温度进行了测量，对比了均值粒径为0.94 和1.55 mm 两种玻璃珠的时变颗粒温度，探究宏观质量流率与介观颗粒温度之间的联系。同时，利用该测量技术高时空分辨率的特点，分析了筒仓颗粒流堵塞过程的弛豫变化特征。主要结论如下。

（1）对比均值粒径为0.94 和1.55 mm 颗粒在筒仓内稳态流动中的质量流率和颗粒温度,发现了质量流率较大的颗粒，其颗粒温度值较低。该现象揭示了介观颗粒的无序运动是控制宏观质量流率的主要因素之一。

（2）发现了筒仓孔口附近存在一个低颗粒温度的特征区域，说明了该位置处的离散颗粒存在定向有序的运动。筒仓孔口两侧的堆积颗粒可以有效减弱颗粒间碰撞产生的接触力是造成该现象的主要原因。

（3）不同粒径颗粒的颗粒温度分布具有一致性。颗粒温度的最大值出现在筒仓顶部区域，并且以“收缩”形式向下扩散传播。在筒仓的不同高度y处，颗粒温度的变化规律是相同的，随着x的增大而减小。然而，在不同的轴向位置处，颗粒温度的值随着y的增大而增大。

（4）利用散斑能见度光谱技术的高时间分辨率的特点，确定了筒仓内颗粒流堵塞的弛豫过程，发现了堵塞过程中的颗粒温度变化满足指数函数分布。并且弛豫时间与筒仓孔口尺寸呈正比例关系。该结果有助于揭示颗粒流随机堵塞的预兆。

本文实验结果揭示了筒仓内颗粒流的运动规律，为完善颗粒材料的传输效率和化工过程的精准控制提供了参考数据。